新型参考电压矢量位置判断方法

郑燕，吴斌，聂伦伦

（1.安徽理工大学电气与信息工程学院，安徽淮南232000；2.中国矿业大学信息与电气工程学院，江苏徐州221008）

1 引言

电压空间矢量脉宽调制（SVPWM）以其直流电压利用率高，输出波形谐波小，易于数字化实现等优点受到了学者们的广泛关注［1-7］。

SVPWM的第一步就是判断参考电压矢量的准确位置，进而找出合成它的3 个电压矢量。然而，随着逆变器电平数的增多，组成其空间矢量图的小三角形个数成平方级数递增，这时传统多电平SVPWM 算法［1-2］对于参考电压矢量所处位置的判断将变得十分复杂、繁琐。

文献［3］将αβ坐标系变换为gh 坐标系，使得所有矢量的坐标变为整数，大大简化了参考电压矢量的定位，但物理意义不明确；文献［4］建立了xyz坐标系，避免了三角函数运算和参考电压矢量幅角求取，但随着电平数的增多，各矢量坐标的求取变得复杂，且含有大量分式和根号；文献［5-6］建立了KL 坐标系，与gh 坐标系一样，物理意义不明确；文献［7］通过建立线电压坐标系，判断小三角形的类型，从而快速地定位了参考电压矢量。

针对此问题，提出了2 种基于αβ坐标系多电平逆变器参考电压矢量位置判断方法。这2种方法相对于传统方法简单、通用且物理意义明确。仿真与实验结果验证所提方法的正确性与可行性。

2 新型参考电压矢量位置判断方法

2.1 判断方法1

参考电压矢量的表达式如下式所示：

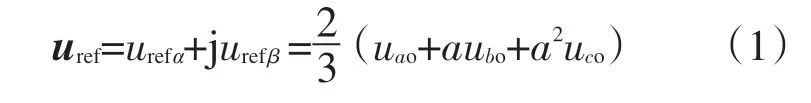
式中：a=ej2π/3；uao，ubo，uco为逆变器三相输出电压。

图1为5电平逆变器的空间矢量图。

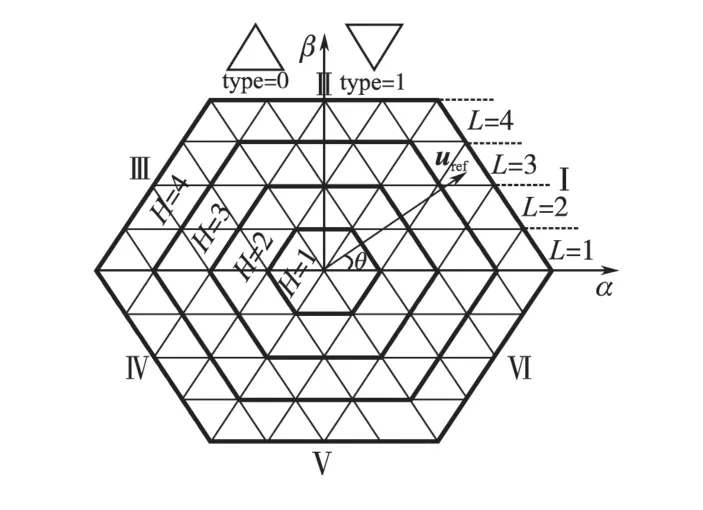
图1 5电平逆变器空间矢量图Fig.1 Space vector diagram of five-level inverter

SVPWM 算法对于参考电压矢量位置的判断一般是先判断出其所处扇区（有些算法不需要），然后再判断其顶点所处的小三角形区域。本文方法1 对于扇区的判断可以采用如下3 种方法。

2.1.1 边界条件法（方法1）

通过简单的算术运算，可以判断上述3条规则的真伪，根据表1 可以判断参考电压矢量所处扇区（“1”表示成立，“0”表示不成立，“”表示无关）。

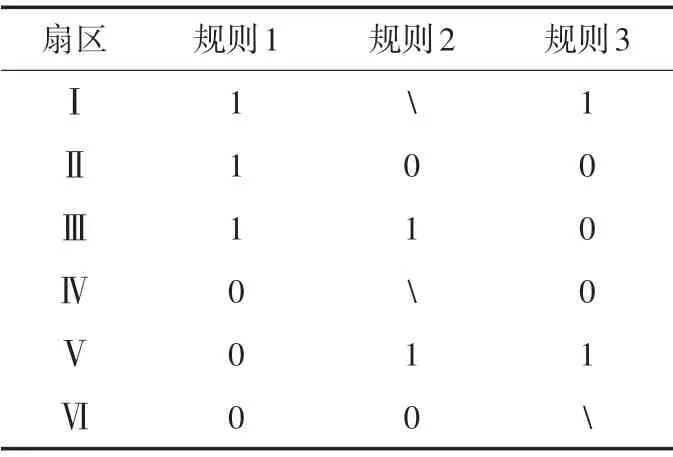
表1 方法1扇区判断Tab.1 Sector judgment of method one

2.1.2 三相电压比较法（方法2）

交流侧系统各相电压为

通过比较三相电压的大小，根据表2 可以判断参考电压矢量所处扇区。

表2 方法2扇区判断Tab.2 Sector judgment of method two

2.1.3 相位角法（方法3）

定义角度r为

则扇区号n（n=1，…，6）可由下式确定：

然后是参考电压矢量顶点所在小三角形的判断，为此，需要先对小三角形的类型（正、倒）进行判断。

令

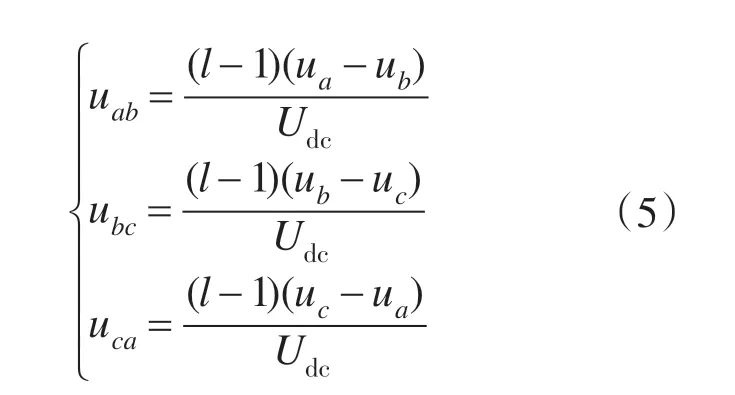
式中：l为逆变器电平数；Udc为直流电源电压。

取

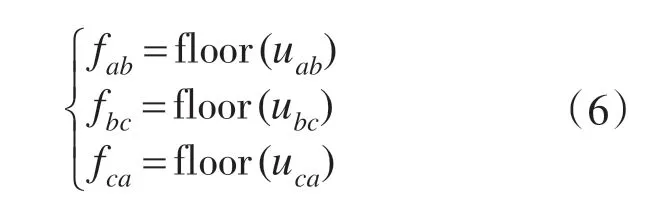
则小三角形类型type（type=0 为正，type=1 为倒）

可由下式判断：

定义调制度mi为

则图1中的六边形号H及小三角形层数L可分别由下式计算：

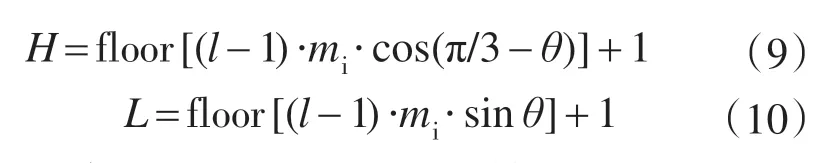
式中：θ为参考电压矢量相对于α轴的相位角。

以三电平逆变器空间矢量图第Ⅰ扇区为例，如图2a所示，判断参考电压矢量顶点所处小三角形的方法如表3所示。

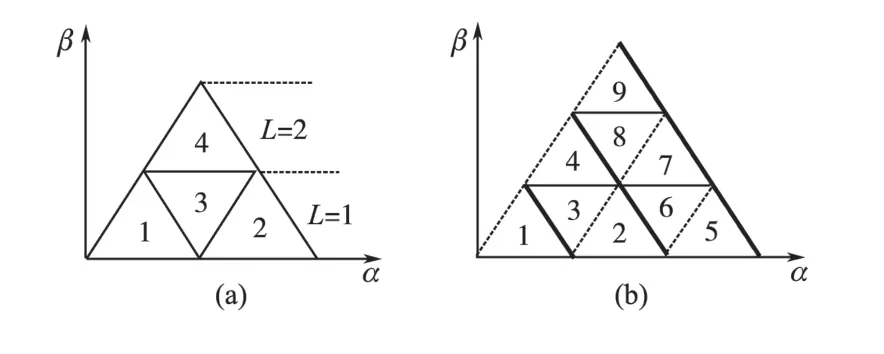
图2 扇区Ⅰ小三角形标号Fig.2 Sector one of small triangles label

表3 方法1小三角形判断Tab.3 Judgment of small triangles of method one

2.2 判断方法2

为不失一般性，以4电平逆变器为例，介绍参考电压矢量顶点所在小三角形的判断方法，图3为其空间矢量图。

图3 4电平逆变器空间矢量图Fig.3 Space vector diagram of four-level inverter

参考电压矢量uref在β轴的分量urefβ可由下式计算得到，

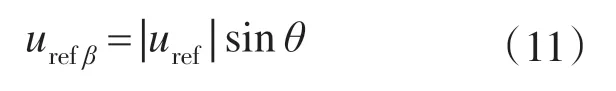
本文方法2 是通过比较urefβ与组成小三角形两条边的直线在竖直方向上的大小关系来判断参考电压矢量顶点所在小三角形的。该方法不需要扇区判断，4 电平逆变器第Ⅰ扇区内参考电压矢量所处小三角形的判断方法，如图2b 和表4所示，其他扇区与之类似。

表4 方法2小三角形判断Tab.4 Judgment of small triangles of method two

3 Matlab仿真分析

3.1 扇区判断

在Matlab/Simulink 仿真环境下，对方法1 所提出的几种判断扇区的方法进行仿真试验，其扇区判断波形如图4所示。

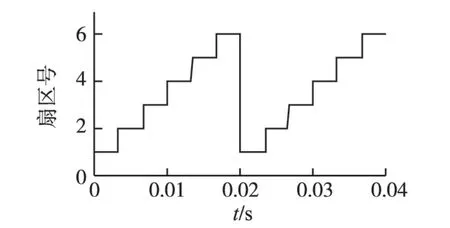
图4 扇区判断波形Fig.4 Sector judgment waveform

3.2 小三角形判断

以三电平逆变器为例，用方法1 对其进行仿真，其空间矢量图中的小三角形标号如图5 所示。图6a 为调制度mi=0.866 时，参考电压矢量扫过的小三角形的仿真波形。以4 电平逆变器为例，用方法2 对其进行仿真，其空间矢量图中的小三角形标号如图5 所示，图6b 为调制度mi=0.94 时，参考电压矢量扫过的小三角形的仿真波形。

图5 小三角形标号Fig.5 Small triangles label

图6 小三角形判断仿真波形Fig.6 Simulation waveforms of small triangles judgment

4 实验验证

基于TMS28335 DSP搭建二极管钳位型三电平实验平台，对本文所提出的两种方法进行验证。主电路直流侧采用2个2 200 μF/400 V的电解电容，开关管采用IRF840 型MOSFET，光耦隔离采用TPL250；吸收电路采用RCD型，电阻为10 Ω，电容为2 μF的无感电容，二极管采用MUR860 超快恢复二极管；负载采用Y 型连接的三相对称阻感负载，电阻值为10 Ω，电感值为5 mH。

图7 为调制度mi=0.8 时的实验线电压、相电流波形。由于本文所提的两种方法的区别在于参考电压矢量位置判断方法不同，SVPWM 算法的其他步骤完全相同，因而两者的输出波形一样。

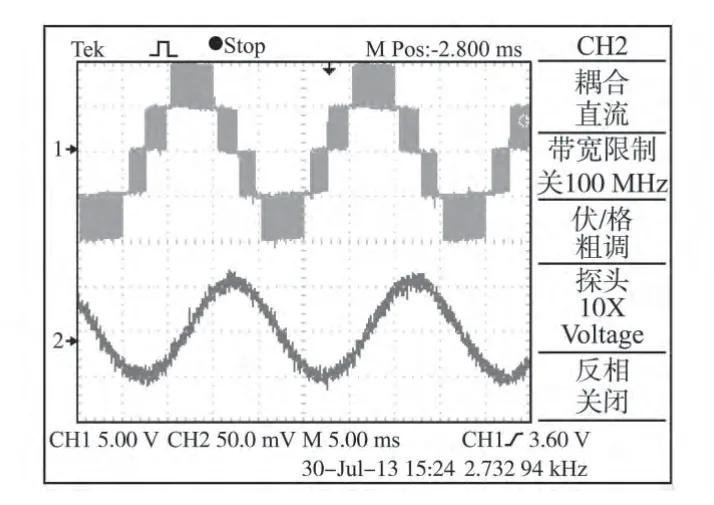
图7 实验线电压和相电流波形Fig.7 Experimental line voltage and phase current waveforms

5 结论

针对传统多电平SVPWM 算法随着逆变器电平数的增多，其对于参考电压矢量的位置判断变得愈加复杂，计算量很大的缺点，提出了2种基于αβ坐标系的简单、通用且物理意义明确的多电平逆变器参考电压矢量位置判断方法。这两种方法比传统方法简单，且更易于理解与数字化编程实现。通过Matlab仿真软件进行了仿真分析，并在实验平台上进行了实验研究，仿真和实验结果验证了所提方法的正确性与可行性。

［1］桂红云，姚文熙，吕征宇.DSP空间矢量控制三电平逆变器的研究［J］.电力系统自动化，2004，28（11）：62-65，74.

［2］鹿水，陈其工，江明.基于MATLAB 的三电平逆变器SVPWM 仿真研究［J］.安徽工程大学学报，2012，27（1）：46-49.

［3］赵辉，李瑞，王红君，等.60°坐标系下三电平逆变器SVPWM 方法的研究［J］.中国电机工程学报，2008，28（26）：39-45.

［4］何广明，何风有，王峰，等.基于坐标分量的三电平SVPWM快速算法［J］.电工技术学报，2013，28（1）：209-214.

［5］姜旭，肖湘宁，赵洋，等.改进的多电平SVPWM及其广义算法研究［J］.中国电机工程学报，2007，27（4）：90-95.

［6］肖湘宁，刘昊，姜旭，等.非正交坐标系多电平SVPWM 及其在DVR 中的应用［J］.电力电子技术，2004，38（4）：20-23，30.

［7］Hou Xuan，Li Yongdong，Liu Yongheng.A Novel General Space Vector Modulation Algorithm for Multilevel Inverter Based on Imaginary Coordination［C］//PEDS2003 Record，2003：201-207.