改进的永磁同步电梯曳引机参数辨识方法

占宏，黄招彬

（华南理工大学自动化科学与工程学院，广东广州510641）

1 引言

无齿轮永磁同步电梯曳引机（专用永磁同步电机）具有能量密度高、调速性能好、效率高等优势，已经逐步成为电梯行业曳引系统的主流驱动设备。永磁同步电梯曳引机一般采用基于转子磁链定向的矢量控制方法，其中电流环PI控制参数由电机的定子电阻、直轴电感、交轴电感计算得到，而启动时的矢量控制解耦角度通过辨识转子磁极初始位置得到（启动之后解耦角度由初始值和编码器测得的角位移计算得到）。故永磁同步电梯曳引系统运行之前，需要对曳引机的定子电阻、电感与转子磁极初始位置进行离线参数辨识。

定子电阻离线辨识一般采用伏安法［1］，即给定子线圈注入一定幅值的电压并检测稳态时的电流，由电压与稳态电流计算出定子电阻。但由于各种电机的电阻差异很大，电压过大会造成过流，电压过小会影响电阻辨识精度，本文方法中注入电压幅值从小到大自动调整，直到稳态电流达到额定电流；同时采用两点式电阻计算方法，消除死区效应与窄脉冲限制的影响。

定子电感离线辨识一般采用电流上升时间常数间接测量方法或基于高频旋转电压注入的直接测量方法［1］，前者根据时间常数与定子电阻计算电感，但是难以区分直轴电感与交轴电感；后者在保持转子静止的情况下分别测量出直轴电感与交轴电感。本文方法中采用幅值自动调整的高频旋转电压注入方法，电压频率根据额定频率和载波频率自动选择。

转子磁极初始位置辨识方法主要有旋转型辨识方法与静止型辨识方法。旋转型辨识方法，即预定位法［2-3］可以精确辨识转子磁极初始位置，但必须在转子空载的情况下运行。而静止型辨识方法［4-10］是基于永磁同步电机凸极效应与转子磁路非线性饱和特性的辨识方法，可以在带载情况下辨识转子磁极初始位置，辨识精度略差，不过能满足电梯应用要求。一般电梯曳引系统需要包含这两种方法，在工况允许空载的情况下采用旋转型辨识方法，否则采用静止型辨识方法。

传统旋转型辨识方法［2-3］一般是在电机空载的情况下给定子某个方向注入一定幅值的电压，由电压产生电流，电流产生转矩使转子运动，直至转子磁极方向与电压方向重合（转矩为零），从而获得转子磁极位置。该方法存在两个问题：注入电压的幅值难以保证产生足够的转矩电流来克服转子摩擦阻力的同时又不导致过流；当注入电压方向刚好在转子磁极的反向时，转子也不会转动，会被误认为是转子磁极方向。本文提出基于电流闭环的两步电流注入方法，电流可控并且可以达到预定的幅值保证足以克服摩擦阻力，同时两步法先给0°方向注入电流将转子拉至0°方向或180°方向，然后给90°方向注入电流，一定能将转子拉至90°方向。

静止型辨识方法主要包括脉冲电压注入法［4-5］、高频旋转电压注入法［6-8］和高频正弦电压注入法［9-10］。其中，脉冲电压注入法会产生转子轻微颤动而降低辨识精度，高频旋转电压注入法的信号解耦运算复杂，只有高频正弦注入法辨识精度高同时实现容易。本文采用注入电压与频率自动调整的高频正弦电压注入法，同时改进了转子磁极极性的判断方法。

2 定子电阻与电感辨识

在永磁同步电机的x轴方向，磁路的非线性饱和特性［11］如图1所示，当磁路中磁链Ψx较小时，磁链Ψx与磁路方向上的电流ix基本呈线性变化；当磁路中磁链Ψx较大时，磁链Ψx与磁路方向上的电流ix逐渐呈非线性变化，即表现出磁路饱和特性。为了充分利用永磁体，永磁同步电机一般会将转子永磁体磁路设计为接近磁路饱和，即永磁体磁链Ψm处于非线性变化区间。

图1 永磁同步电机的非线性磁路饱和Fig.1 Nonlinear magnet flux saturation in PMSM

永磁同步电机按转子结构分类可分为内嵌式永磁同步电机（interior permanent magnet synchronous motor，IPMSM）和表贴式永磁同步电机（surface-mounted permanent magnet synchronous motor，SPMSM）。其中，IPMSM 具有明显的结构凸极效应，即d轴电感小于q轴电感，即Ld0＜Lq0；而SPMSM 没有明显的结构凸极效应，即d轴电感与q轴电感相等，即Ld0=Lq0。由于磁路非线性饱和特性导致Ld1＜Ld0，故无论IPMSM还是SPMSM，都满足Ld1＜Lq0。

在工作点附近记d轴磁阻、q轴磁阻、d轴磁阻变化率与q轴磁阻变化率分别为

显然有Rd＞Rq。在永磁同步电机q轴方向，磁链完全由电流产生，没有永磁体磁链分量，故在Ψq=0附近磁链Ψq与电流iq的关系近似表示为

在永磁同步电机d轴方向，磁路中存在永磁体磁链Ψm，故在Ψd=Ψm附近磁链Ψd与电流id的关系近似表示为

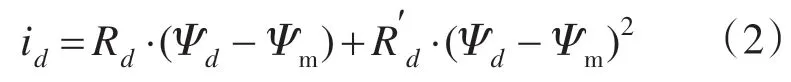
设静止坐标系为αβ，以转子磁极方向定向的旋转坐标系为dq，以预定角度定向的预定坐标系为，如图2 所示。基于转子磁链定向的矢量控制中，在旋转坐标系dq中，永磁同步电机等效电路方程为

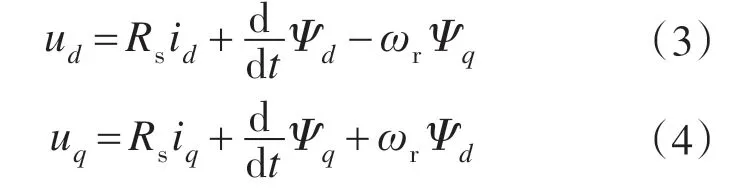
式中：ud，uq分别为d轴与q轴电压；id，iq分别为d轴与q轴电流；Rs为电枢绕组相电阻；ωr为转子角速度。

图2 预定坐标系中的电压注入图Fig.2 Voltage injection in the destined reference frame

永磁同步电机的定子电阻辨识采用两点式伏安法。给定子电压空间中60°方向注入电压ures（电压均是以母线电压Udc为基准的标幺值，，如图2所示，电流稳定后的轴电流为ires（电流均是以电机额定电流峰值为基准的标幺值）。

为了消除脉宽调制中的死区效应与窄脉冲限制影响，采用两点式电阻测量方法，即测量2个不同电压注入下的电流响应，然后用电压差值除以电流差值即为定子电阻。为保证不会因注入电压过大而造成过流，注入电压ures从较小值（如0.05）开始步进增加，步长为0.01，直到ires＞0.8后结束。记录ires＞0.8之前与之后的电压与电流，分别为ures1，ires1，ures2，ires2，同时记录ires＞0.8之后A 相、B 相、C 相稳态电流分别为Ia，Ib，Ic。记Δures=ures2-ures1，Δires=ires2-ires1，那么定子电阻Rs为

同时，可根据Ia，Ib，Ic进行故障诊断。定子电阻辨识与故障诊断具体流程如图3 所示。图3 中，数据1：ures1，ires1；数据2：ures2，ires2，Ia，Ib，Ic；条件1：|Ia|＞0.5且|Ib|＞0.5且|Ic|＞0.5?条 件2：|Ia-Ib|＞2×ΔImax?其中ΔImax为电流检测允许误差上限。

图3 定子电阻辨识与故障诊断Fig.3 Stator resistance identification and fault diagnosis

永磁同步电机电感辨识采用幅值自动调整的高频旋转电压注入方法。给定子注入高频旋转电压，则

由于注入电压频率足够高，转子基本保持静止，即ωr=0，同时ωcLd≫Rs，ωcLq≫Rs，可忽略定子电阻，故式（3）与式（4）可简化为

文献［1］根据忽略磁路非线性饱和时Is的最大值与最小值来计算直轴电感与交轴电感，而实际上Is受影响，如式（9）所示，使得最大值更大，最小值可能更小。本文采用改进的测量方法，可以削弱甚至消除磁路非线性饱和的影响。

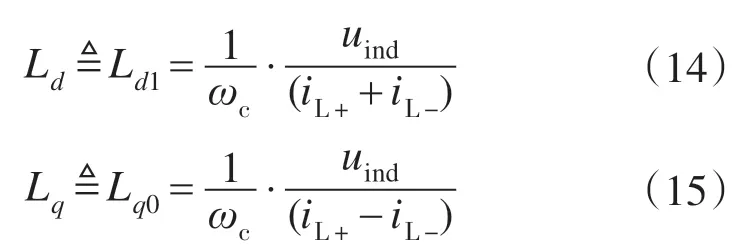
为保证定子电感辨识过程中转子基本不转动且感抗远大于电阻，要求注入电压旋转频率fc远大于电机额定频率frtd；又因为旋转频率fc受载波频率fcw限制，所以旋转频率必须满足frtd≪fc＜fcw。

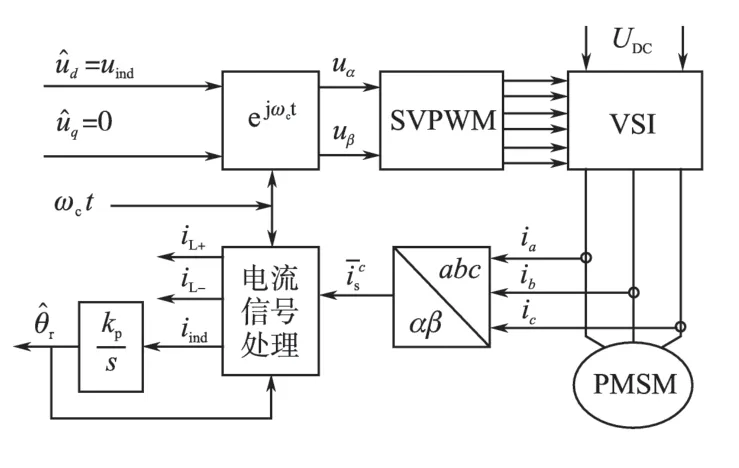
图4 定子电感辨识原理Fig.4 Stator inductance identification theory

与定子电阻辨识同理，为保证不会因为注入电压uind过小导致iL+与iL-过小，从而影响电感检测精度，注入电压uind从较小值（如0.20）开始步进增加，步长为0.05，直到电流平均年幅值Is_av足够大（如Is_av≥0.2）或者输出电压达到最大输出（如uind≥0.9），然后以此幅值持续注入高频旋转电压（如1 s）检测iL+与iL-，结束后根据式（14）与式（15）计算定子电感。电感辨识具体流程如图5所示。

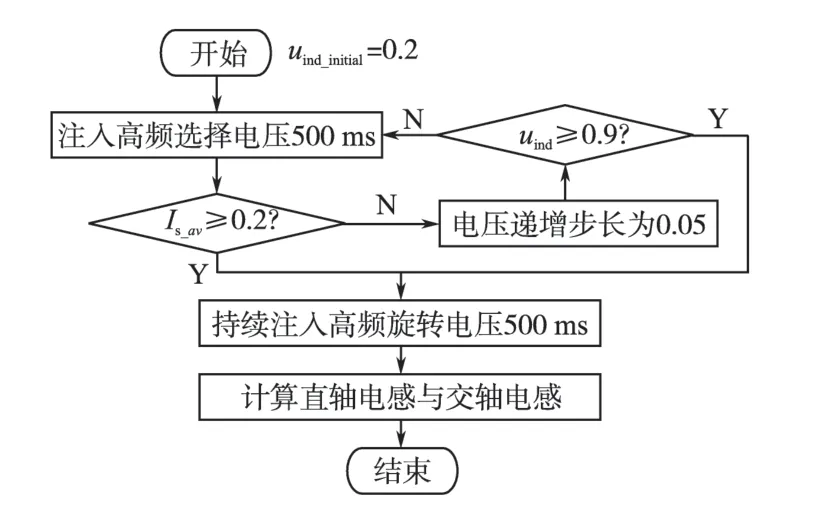
图5 定子电感辨识流程图Fig.5 Stator inductance identification flow chart

根据辨识出的定子电阻与电感，可得到矢量控制系统中d轴电流环和q轴电流环的PI 参数分别为

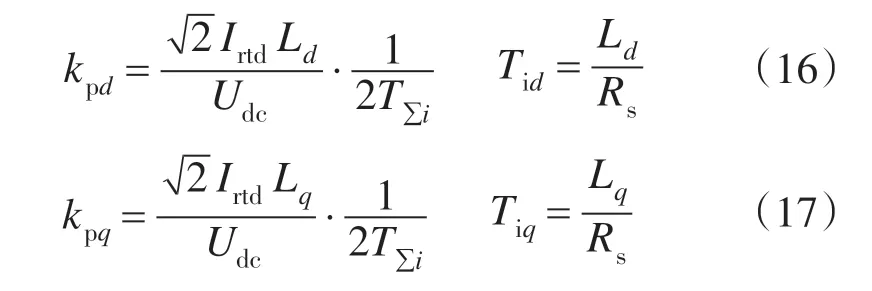
式中：T∑i为PWM输出与电流检测总延时。

3 旋转型转子磁极初始位置辨识

永磁同步电机的旋转型转子磁极初始位置辨识采用基于电流闭环的两步电流注入法［2］。预定坐标系中的电流注入方法如图6 所示，其中电流环PI参数按照式（16）与式（17）设置。

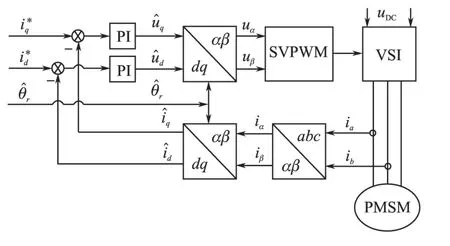
图6 预定坐标系中的电流注入图Fig.6 Current injection in destined reference frame

两步电流注入法中先给=0°方向注入电流irot，将转子拉到0°方向或者180°方向；待转子稳定后，再给=90°方向注入同样大小的电流irot，将转子拉到0°方向。在一步电流注入法中，如果直接在=90°方向注入电流，而实际转子在θr=270°位置，此时也不产生转矩，使得定位错误，而两步电流注入法可以避免辨识盲区。两步电流注入法具体流程如图7所示。

图7 旋转型转子磁极位置辨识Fig.7 The rotating method for rotor position

改进的旋转型转子磁极初始位置辨识方法，不仅可以无盲区的辨识转子位置，同时电流完全可控且其大小与方向均采用渐变方式，有效避免了转子振荡问题。

4 静止型转子磁极初始位置辨识

永磁同步电机的静止型转子磁极初始位置辨识采用基于高频正弦电压注入的转子位置辨识方法［9］。给定子方向注入高频正弦电压，如图8所示，，那么

在高频正弦电压注入下，转子基本保持静止，即ωr=0；同时ωcLq＞ωcLd≫Rs，可忽略定子电阻Rs压降影响，故式（3）与式（4）可简化为

图8 转子磁极辨识高频正弦电压注入法Fig.8 High frequency sinusoidal voltage injection for rotor position identification

根据式（1）、式（2）与式（19）得到旋转坐标系电流与预定坐标系电流分别为

对式（21）进行如下信号处理得到转子位置信息ipos与转子极性信息ipol为

由式（22）可知，在Δθ∈(-π/2,π/2)范围内，当Δθ＞0时，ipos＞0；当Δθ＜0时，ipos＜0。根据ipos的特性，可设计图8 所示闭环负反馈结构，最终使得ipos→0，即Δθ=0或Δθ=π，即得到转子磁极位置的初次转子角度。然后再根据式（23）判断转子磁极极性，若ipol＜0，则Δθ=0；若ipol＞0，则Δθ=π。为保证在θr=0,π/2,π,3π/2 4 个奇异点时该方法依然可行，可以先注入一定时间正弦电压观测ipos，若ipos始终为0，则将初值重置为π 4继续进行闭环调节。基于高频正弦电压注入的静止型转子磁极初始位置具体实现如图9所示。

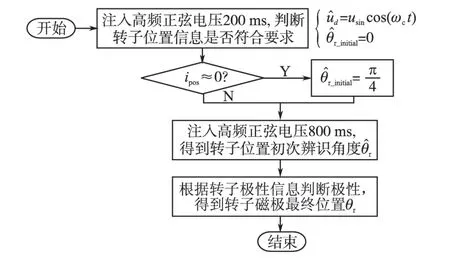
图9 静止型转子磁极位置辨识Fig.9 The standstill method for rotor position

5 实验

采用基于TMS320F28035控制器的电梯伺服控制系统，以浙江玛拓驱动设备有限公司的型号MY02-1000/175T表贴式永磁同步电梯曳引机为实验对象，进行离线参数辨识方法的实验，曳引机参数为：额定电流26 A，额定功率11 kW，额定频率33.4 Hz，额定电压380 V，额定转速167 r/min，线反电势276 V/（kr·min-1），额定转矩640 N·m，相 电 阻0.395 9 Ω，额定梯速1.75 m/s，电感16.5 mH，额定载重1 000 kg，极数P=24。

实验先辨识定子电阻，然后辨识直轴电感和交轴电感，最后采用旋转型或者静止型转子磁极位置辨识方法进行转子磁极初始位置辨识。

一次离线参数辨识过程的信号波形如图10所示（信号均采用标幺值，角度以2π为基准标幺化），定子电阻辨识经历了5 次注入电压递增（0～2.5 s区间）；定子电感辨识经历了4次注入电压递增（2.5～5.0 s 区间）；旋转型转子位置辨识过程中电流跟踪效果非常好（5.0～11.0 s区间），间接说明电阻与电感测量基本准确；静止型转子辨识过程中（5.0～6.0 s区间），转子角度在0.2 s之内基本调节稳定。

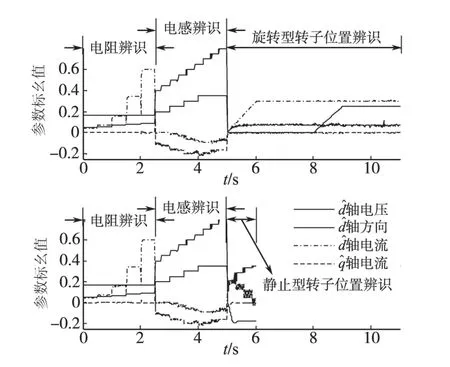
图10 离线参数辨识过程的信号波形图Fig.10 Signal waves of offline parameter identification

对永磁同步电梯曳引机一对极下等分为20个测试点（用编码器ERN1387校准），对每个测试点进行定子电阻、电感与静止型转子磁极位置辨识，得到辨识结果如图11 所示。其中，定子电阻的辨识平均值为0.385 6 Ω，标准差为0.013 6 Ω；直轴电感平均值为12.45 mH，标准差为0.105 1 mH；交轴电感平均值为16.73 mH，标准差为0.138 0 mH。与标称值比较，定子电阻与交轴电感测量都比较准确，直轴电感测量由于受磁路饱和影响会比交轴电感略小，其测量结果也与预期相符。静止型转子磁极位置辨识误差平均值为1.191°，标准差为2.087 1°，精度完全满足电梯行业应用要求。

图11 永磁同步电梯曳引机一对极下的离线参数辨识效果Fig.11 Offline parameter identification result under one pair of poles of PMSTM

6 结论

改进的永磁同步电梯曳引机离线辨识方法中，采用注入电压自动适应的两点式伏安法测定定子电阻，消除了PWM 调制中死区效应与窄脉冲限制的影响；采用注入电压幅值自动适应的高频旋转电压注入法测定定子电感，削弱了转子磁路非线性饱和对直轴电感测量的影响。旋转型转子磁极辨识方法采用基于电流闭环的两步电流注入法，平滑的电流变化与角度变化保证了辨识过程中转子基本不会振荡。静止型转子磁极辨识方法采用高频正弦电压注入法，运算量小，辨识精度高；同时改进的转子极性判断方法不需要额外注入脉冲电压，缩短了辨识时间。通过在永磁同步电梯曳引机上的反复试验，其结果验证了该方法的可行性与可靠性。

［1］曾祥云.永磁同步电机无位置传感器控制技术研究［D］.上海：同济大学，2009.

［2］胡任之.永磁同步电机转子初始位置估计［D］.哈尔滨：哈尔滨工业大学，2008.

［3］Ostlund S，Brokemper M.Sensorless Rotor-position Detection from Zero to Rated Speed for an Integrated PM Synchronous Motor Drive［J］.Industry Applications，IEEE Transactions on，1996，32（5）：1158-1165.

［4］Nakashima S，Inagaki Y，Miki I.Sensorless Initial Rotor Position Estimation of Surface Permanent-magnet Synchronous Motor［J］.Industry Applications，IEEE Transactions on，2000，36（6）：1598-1603.

［5］韦鲲，金辛海.表面式永磁同步电机初始转子位置估计技术［J］.中国电机工程学报，2006，26（22）：104-109.

［6］Haque M E，Limin Z，Rahman M F.A Sensorless Initial Rotor Position Estimation Scheme for a Direct Torque Controlled Interior Permanent Magnet Synchronous Motor Drive［J］.Power Electronics，IEEE Transactions on，2003，18（6）：1376-1383.

［7］王高林，杨荣峰，于泳，等.内置式永磁同步电机转子初始位置估计方法［J］.电机与控制学报，2010，14（6）：56-60.

［8］周元钧，蔡名飞.改进的永磁同步电机转子初始位置检测方法［J］.电机与控制学报，2010，14（3）：68-72.

［9］刘颖，周波，李帅，等.转子磁钢表贴式永磁同步电机转子初始位置检测［J］.中国电机工程学报，2011，31（18）：48-54.

［10］Gaolin W，Guoqiang Z，Rongfeng Y，et al.Robust Low-cost Control Scheme of Direct-drive Gearless Traction Machine for Elevators Without a Weight Transducer［J］.Industry Applications，IEEE Transactions on，2012，48（3）：996-1005.

［11］Bianchi N，Bolognani S，Ji-Hoon J，et al.Comparison of PM Motor Structures and Sensorless Control Techniques for Zerospeed Rotor Position Detection［J］.Power Electronics，IEEE Transactions on，2007，22（6）：2466-2475.