球磨机运动动能与存煤量的DEM试验研究
何 芳,白 焰,张 然
(华北电力大学 控制与计算机工程学院,北京102206)
球磨机粉磨机理至今未统一,在存煤量的监测和控制问题上缺乏更完善精准的方法,致使提高磨煤机效率、降低能耗等方面的研究还未取得突破性进展.首先,如何准确测量和控制球磨机存煤量成为问题关键和技术难点.对系统的控制要求保证球磨机存煤量接近最佳存煤量,目前的检测方法有差压法、振动法、噪声法、超声波法、功率法及多种方法结合等,但这些方法均因局限性大、精准性差等原因不能如实反映球磨机内的存煤量[1-2].其次,球磨机介质运动形态虽然直接影响磨煤功耗和效率,与粉磨机理的研究密切相关,但业内人士大多从介质运动轨迹或介质分区来探讨介质本身的运动规律及球磨机工作参数对介质运动的影响.Lu等[3-4]通过试验研究球磨机内抛落钢球的运动轨迹并建立钢球运动方程,提出较系统的磨矿理论;Guo等[5]研究了磨煤机转速率、球荷填充率等多种因素对钢球运动的影响.此外,国内外学者进行了大量实验研究,提出纯二相运动理论等多种介质运动形态理论[6].笔者在定量优化的工作参数配置下对球磨机进行离散元素法(DEM)仿真分析[7],通过直接观察球磨机内不同存煤量的钢球运动,记录钢球动能的实时仿真实验数据,分析不同工况下介质钢球的冲击动能与球磨机存煤量的关系,在一定程度上有助于实现更好的球磨机存煤量的控制,提高制粉效益.
1 钢球运动过程分析
筒体内存煤量是影响钢球运动状态的一大因素,当磨煤机筒体定轴匀速转动时,筒体内钢球随存煤量增加出现不同的运动状态,其中:
(1)在圆周及泻落运动区域,筒体中存煤量很少甚至为空,钢球和煤随筒体一起做匀速圆周运动或泻落运动,钢球与钢球的撞击概率变大,钢球、煤块及磨煤机衬板之间主要受磨削作用,且摩擦增强,造成不必要的钢球磨耗和衬板磨平,磨煤效率低下;
(2)在抛落运动区域,存煤量正常且不超过最外层钢球落回点,钢球在底脚区对煤主要起冲击作用,实现钢球磨煤的周期循环碰撞,磨煤效率高;
(3)在球磨机中心周围区域,钢球圆周运动和抛落运动混合,范围受限,磨削、冲击作用微弱;
(4)在空白区域,钢球无运动或做圆周运动,当筒体存煤量过多时,钢球运动范围小,分布相对筒体不动,造成资源浪费,易出现运行故障.
2 DEM 试验
2.1 试验原理
DEM 是一种求解与分析颗粒材料运动规律与动力学参数的新型非连续介质力学的数值计算方法.DEM 将散粒体分离成离散单元的集合,单元本身具有一定的几何、物理和化学特性.介质运动受牛顿第二定律控制,用动态或静态松弛法迭代求解,通过各单元的运动和位置描述整个介质的运动规律.
由牛顿第二定律可以得到颗粒i的运动方程为
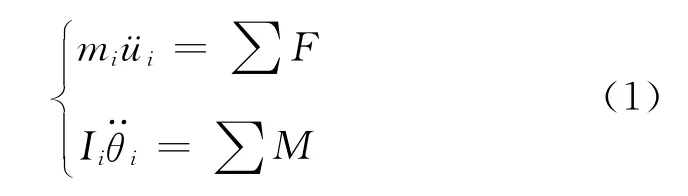
常用中心差分法对式(1)进行数值积分,得到以2次迭代时间步长的中间点表示的更新速度为

通过对式(2)积分,得到关于位移的式(3)

式中:ui、θi分别为颗粒i的位移和角位移.
由颗粒的新位移值计算新作用力,满足力与位移关系,反复循环跟踪每个颗粒在任意时刻的运动,从而得到整个散粒体的运动形态.
2.2 PFC3D 模 型
PFC3D 是将离散元方法用于模拟任意形状、大小的二维圆盘或三维球体集合体的运动及其相互作用的颗粒分析三维数值程序,特别适合复杂机理性问题的探索,从本质上研究固体(固结和松散)介质的力学特性.PFC3D 模拟试验可以代替离线试验,既可解决静态问题也可解决动态问题,既可用于参数预测,也可用于原始资料详细但实测资料相对较少情况下的实际模拟[8],从微观结构角度表示宏观物质的物理特性.
笔者采用的PFC3D 模型具有如下优势:(1)规定了钢球和煤质的受力情况和边界条件,颗粒的堆积过程自然呈现;(2)可方便确定钢球和煤质堆积体系的任意位置和大小,相应得到钢球动能、摩擦损失能量和筒体总功;(3)软件可直接生成钢球和煤质堆积体系的三维图像,简化了可视化过程.
2.3 均衡接近度
关联度是一种接近性度量,为减少局部点关联倾向,进一步采用均衡接近度来测定比较列的关联系数列的均衡程度[9].简要概述为:首先得到比较列j与参考列i的关联系数分布映射,i=1、2、…、m,j=1、2、…、n;然后计算关联系数熵H⊗(Rij);进一步求得均衡度
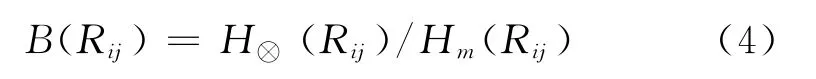
其中,Hm(Rij)表示为ln(数列个数),是比较列j的最大熵.则均衡接近度为

其中,γ为关联度.
因此依据均衡接近度的排序确定参数关系,结合参数的物理意义获得有效理论.
3 存煤量与钢球动能模型
由于介质运动的高速性、离散性、随机性及存煤量的不确定性,使得传统方法难以分析存煤量变化时球磨机内部研磨介质的运动状态和粉磨机理.因此,球磨机仿真分析越来越受到业内人士的关注.磨煤机钢球属于非连续体,而基于命令驱动模式的PFC3D 模型处理不连续问题较好,能更真实地反映钢球的运动规律,因此,笔者利用其显式差分算法和离散元理论来模拟计算随存煤量增加的钢球运动动能的变化.
3.1 PFC3D模型参数的选定
依据工业球磨机的特点,为提高模型的仿真效果,将球磨机筒体抽象为具有某种材料特性的圆柱体,规格为有效内直径0.4m、长度1.2 m,其内壁固定特定数量的非光滑耐磨钢衬板,从轴向上截取原长度的1/6为筒体边界.筒体内钢球和煤质抽象为具有特定材料特性与尺寸参数的球形离散单元,球径Db有0.03m 和0.04m2种,堆积密度ρgq=4.9t/m3,煤粒的半径(煤径)Rm分别为3 mm、4 mm、5mm、6mm、7mm 和8mm,堆积密度为ρm=0.75t/m3.基于颗粒模型和接触模型中球磨机各参数在定量重叠系数、泊松比和恢复系数条件下的仿真变化范围[10],结合不同材质性能和实践经验设定其他模型参数的合理值(见表1).选定球磨机工作转速与临界转速之比,即转速率Φ=80%,基于以上参数的优化配置,通过设置黏性阻尼,生成圆柱、螺旋壁面等初始参数,建立球磨机筒体模型,载入介质煤和钢球,对随存煤量增加的钢球运动状态进行仿真模拟,实时记录球荷的动能和受力变化.

表1 模型参数表Tab.1 Model parameters
3.2 PFC3D 模型的建立
离散元素法的基本假设非常重要,是离散元素法的前提条件,本文的基本假设如下:
(1)颗粒单元为刚性体和球形;
(2)接触发生在很小的范围内,即点接触,且接触处有特殊的连接强度;
(3)接触特性为柔性接触,接触处允许有一定的与颗粒尺寸相比很小的“重叠”量,大小与接触力有关;
(4)时间步长足够小,避免非直接接触的任何单元扰动,且在任意时间步长内速度和加速度恒定.
PFC3D 模型中接触形式有球-球接触与球-墙(球-壁)接触2种.通过设定钢球和煤介质的接触模型、边界条件、受力情况和颗粒性质来模拟生成颗粒体系运动过程的三维图像.每一个筒体在转速率Φ下均有一个最佳钢球充满系数(装球率)[11]

则最佳钢球装载量

钢球个数的近似计算公式为[12]
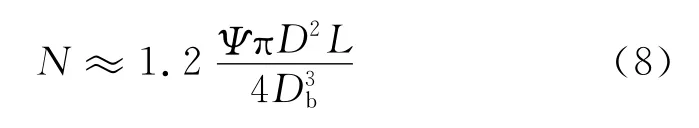
式中:Ψ为球磨机装球率,%;L为球磨机筒体的有效长度,m;D为筒体有效内直径,m.
经计算得出2种球径下仿真钢球的个数分别约为N0.03=200和N0.04=86.基于这2种参数条件,分析随存煤量的增加,参数球荷运动动能、滑动摩擦损失能量和筒壁总功的变化趋势.
4 结果与分析
基于PFC3D 软件平台,存煤量增加满足初始值a(1)=100,d=200,a(7)=1 300的等差数列,筒体以5.6rad/s匀速转动4圈的仿真试验结果如下.
4.1 Db=0.03m、N0.03=200的钢球动能分析
图1给 出 了Db=0.03 m、N0.03=200 的PFC3D 模型效果图.图1(a)表示加入Rm=3mm、Nm=700的煤粒后,球磨机筒体在运行处于稳态时的钢球分布和运动状态,图1(b)表示筒体转动后,球荷所获动能值的实时变化曲线,初步得出抛落的钢球和存煤量达到一定值后球荷动能出现明显峰值,且循环转动中动能有规律地波动变化.

图1 Db=0.03m、N0.03=200的PFC3D模型效果图Fig.1 Effect chart by PFC3D model for Db=0.03m,N0.03=200

表2 不同煤径和存煤量下的钢球运动值Kpj/Ww-Kpj0/Ww0(Db=0.03m、N0.03=200)Tab.2 Ball motion parameters for different particle sizes and storage of coal(Db=0.03m,N0.03=200) %

图2 存煤量与各能量值的散点图(Db=0.03m、N0.03=200)Fig.2 Scatter diagram of coal storage and energy values(Db=0.03m,N0.03=200)
表2和图2给出了随存煤量不断增加,钢球获得的实时动能的最大值和平均值、滑动摩擦损失能量及筒壁总功的结果.其中,Kpj0/Ww0表示无煤状态下筒体匀速转动4圈的动能平均值占筒壁总功的百分比.表2中,不同煤径下钢球对煤质的做功量随存煤量增加均先增大后减小,Rm=3 mm、Nm=700时,球荷动能占筒壁总功的百分比Kpj/Ww高出无煤状 态 时2.829 4%,即Kpj/Ww-Kpj0/Ww0=2.829 4%,钢球冲击破碎煤质效率最高;当Rm≥6 mm 时,球荷动能值随着存煤量的增加越来越小,Rm=8mm 时已无抛落冲击现象,钢球以研磨、挤压作用为主.可见,不同球磨机型和参数设定适宜有限的煤质直径.图2中,可以清晰地看到不同煤径下球荷实时动能的最大值和平均值、滑动摩擦损失能量及筒壁总功随存煤量增加的变化趋势,为体现曲线变化程度,将球荷动能的最大值和平均值分别扩大10倍,其中Ww-Kpj×10表示筒壁总功与钢球动能平均值扩大10倍后的差值.由此可见,摩擦做功和筒壁做功变化基本一致,当Ww-Kpj×10大于极小值后呈逐渐增大趋势,筒壁做功明显升高,而球荷动能变化不大,曲线极小值点对应最佳存煤量,进一步说明存煤量超出一定值后,球磨机有用功减少,钢球动能利用率降低,钢球运动的实时动能与存煤量、磨煤机运行效率存在密切关系.
4.2 Db=0.04m、N0.04=86的钢球动能分析
图3给出了Db=0.04m、N0.04=86的PFC3D模型效果图.图3(a)表示磨煤机筒体在运行处于稳态、所加入的86 个钢球获得最大动能时,Rm=3 mm、Nm=700的煤粒的PFC3D 分布和运动状态,图3(b)表示筒体转动后,图3(a)中的相应球荷所获动能值的实时变化曲线.随着存煤量的不断增加,钢球获得的实时动能的最大值和平均值、滑动摩擦损失能量及筒壁总功如表3和图4所示.
由表3和图4可知,相对于表2和图2,钢球直径增大0.01m,不同煤径及存煤量下球荷动能增幅变小,但在Rm≤6 mm 时,球荷动能值随存煤量增加仍具有先增大后减小的规律,煤径越大,动能峰值对应的最佳存煤量越少,而Ww-Kpj×10随存煤量增加几乎均呈现明显的增长趋势但有极小值点,可见,钢球在筒体中的运动范围有限,当超出最佳存煤量后冲击能力逐渐减弱,研磨逐渐起主导作用,受球径和煤径影响,最佳存煤量亦不同.
4.3 存煤量与钢球动能的关联分析
由DEM 仿真得到的结果可以明显看出,球磨机运行过程中存煤量与钢球实时动能之间存在密切关系.将实验数据中的存煤量选为母序列,其他表征参数(钢球动能、摩擦损失能量和筒壁总功)为子序列,计算均衡接近度值,结果发现各参数的均衡接近度均超过0.6,说明各参数对存煤量的变化程度灵敏度较高,而参数钢球动能比摩擦损失能量和筒壁总功的均衡接近度值稍高,能更好地解释存煤量,反映运行效率.

图3 Db=0.04m、N0.04=86的PFC3D模型效果图Fig.3 Effect chart by PFC3D model for Db=0.04m,N0.04=86

表3 不同煤径和存煤量下的钢球运动参数值Kpj/Ww-Kpj0/Ww0(Db=0.04m、N0.04=86)Tab.3 Ball motion parameters for different particle sizes and storage of coal(Db=0.04m,N0.04=86) %

图4 存煤量与各能量值的散点图(Db=0.04、N0.04=86)Fig.4 Scatter diagram of coal storage and energy values(Db=0.04,N0.04=86)
在图1和图3中,钢球和煤质在筒体转动过程中经历泻落、少数抛落到大多数抛落,动能值逐渐达到峰值,抛落运动是钢球最佳运动状态,此时磨煤效率最高;在表2和表3中,适宜的煤径、存煤量条件下,相对无煤状态下,钢球动能平均值占筒壁总功的比例表现出先增大后减小的趋势;在图2和图4中,适宜煤径下存煤量增加,钢球对煤质做功相比筒壁总功的差值存在极小值,而该差值随后明显增大,钢球动能利用率先增大后减小,磨煤效率先逐渐升高后降低.由此可知,钢球实时动能更能准确地反映球磨机筒体内的存煤量,得出最高磨煤效率时对应最大钢球动能的最佳存煤量.同时,摩擦做功和筒壁总功进一步反映钢球冲击力的利用程度,多角度体现球磨机磨煤效率.
5 结 论
(1)得到球磨机内在定量优化的工作参数配置下不同存煤量的钢球运动状态,验证了DEM 仿真模型的有效性和细致分析球磨机内部介质运动动能参数的能力.
(2)钢球抛落确实较泻落状态用于磨煤碎煤的能量多,磨煤效率高. (3)钢球实时动能首次作为检测和控制存煤量的重要参数,与存煤量、磨煤效率关系密切,其随着合适煤径的存煤量的增加先增大后减小,能更准确地反映存煤量的变化情况.
(4)从能量角度探索了球磨机粉磨机理,为基于钢球动能的存煤量控制方法的实现和完善做理论和实验准备.
[1]杨建华,杨海瑞,岳光溪.循环流化床锅炉改变床存量的燃烧试验[J].动力工程,2009,29(6):512-517. YANG Jianhua,YANG Hairui,YUE Guangxi.Combustion test by changing bed inventory on circulating fluidized bed boiler[J].Journal of Power Engineering,2009,29(6):512-517.
[2]OZKAN A,YEKELER M,CALKAYA M.Kinetics of fine wet grinding of zeolite in a steel ball mill in comparison to dry grinding[J].International Journal Mineral Processing,2009,90(1/2/3/4):67-73.
[3]LU Shengyong,MAO Qiongjing,PENG Zheng,et al.Simulation of ball motion and energy transfer in a planetary ball mill[J].Chin Phys B,2012,21(7):1-9.
[4]ROSENKRANZ S,BREITUNG-FAES S,KWADE A.Experimental investigations and modelling of the ball motion in planetary ball mills[J].Powder Technology,2011,212(1):224-230.
[5]GUO Jintang,HU Guang,CHEN Zhikun.Synthesis of novel electron donors and their application to propylene polymerization[J].Transactions of Tianjin University,2012,18(1):8-14.
[6]CHAI T Y,ZHAI L F,YUE H.Multiple models and neural networks based decoupling control of ball mill coal-pulverizing systems[J].Journal of Process Control,2011,21(3):351-366.
[7]胡国明.颗粒系统的离散元素法分析仿真——离散元素法的工业应用与EDEM 软件简介[M].武汉:武汉理工大学出版社,2010.
[8]CLEARY P W.Industrial particle flow modelling using discrete element method[J].Engineering Computations,2009,26(6):698-743.
[9]王建国,何芳,邸昊.电磁抑垢实验中磁场作用与电导率及pH 值的关联分析[J].化工学报,2012,63(5):1468-1473. WANG Jianguo,HE Fang,DI Hao.Correlation analysis of magnetic field and conductivity,pH value in electromagnetic restraint of scale formation[J].CIESC Journal,2012,63(5):1468-1473.
[10]刘璘.离散元素法在球磨机研究中的应用[J].南阳理工学院学报,2012,4(4):62-66. LIU Lin.Application of discrete element method in the ball study[J].Journal of Nanyang Institute of Technology,2012,4(4):62-66.
[11]叶江明.电厂锅炉原理及设备[M].3版.北京:中国电力出版社,2010.
[12]张骁博,杨建国,赵虹.钢球磨煤机制粉系统运行优化的试验 研 究[J].动 力 工 程 学 报,2010,30(2):133-137. ZHANG Xiaobo,YANG Jianguo,ZHAO Hong.Operation optimization of a ball mill pulverizing system[J].Journal of Chinese Society of Power Engineering,2010,30(2):133-137.

