基于频谱校正的傅里叶变换滤波差分吸收光谱监测实验研究

郑海明，吴 浩，李广杰

（华北电力大学 能源动力与机械工程学院，保定071003）

随着工业化进程的飞速发展和人口的急剧增加，全球环境日益恶化，世界性的环境问题直接威胁着各国的经济与社会发展.近年来，环境问题尤其是大气污染问题成了人们关注的焦点.

差分吸收光谱（Differential Optical Absorption Spectroscopy，DOAS）最初由德国海德堡大学环境物理研究所的Platt等人于20世纪70年代提出，并用于测量大气中污染气体浓度，后来逐渐在环境监测领域得到广泛应用［1-3］.根据燃煤火电厂烟气排放SO2、NO2等气体在紫外特征吸收波段的准周期性，笔者在傅里叶变换（FFT）滤波法基础上引入频谱校正，对实测光谱数据进行质量浓度反演，并模拟了实际可能出现的谱线漂移情况，对传统的最小二乘法、FFT 滤波法与校正FFT 滤波法进行了气体监测的对比实验研究.

1 DOAS理论与方法

1.1 DOAS基本原理

DOAS的理论基础是Lambert-Beer定律，其数学表达式为

式中：I0（λ）为由某种合适的辐射源发出的初始辐射强度；I（λ）为通过光程为L的物质后的辐射强度；c为被测气体的浓度；σ（λ）为在波长λ处的吸收截面，可以在实验室测量得到.

气体浓度c可由下式计算：

定义

D（λ）称为光学密度（Optical Density），则：

但在实际测量中，光程中不仅仅存在一种气体，而且还包括瑞利散射εR（λ）和米散射εM（λ）引起的消光［3］.考虑到上述因素，实际气体吸收的辐射强度应按照修正的Lambert-Beer定律计算：

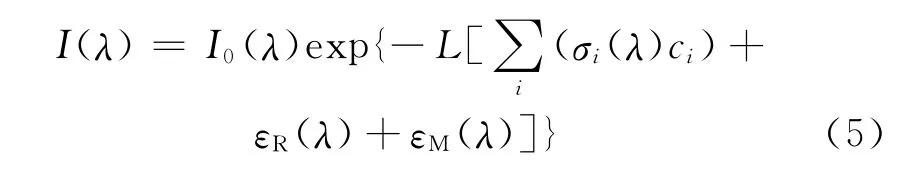
在气体测量过程中由瑞利散射和米散射引起的光学密度在随波长而缓慢变化，而由分子吸收引起的光学密度随波长快速变化，用高通滤波的方法能消除这些消光因素的影响.

为消除瑞利散射和米散射的影响，将吸收截面σi（λ）分成两部分：

式中：σi0（λ）表示随波长缓慢变化的吸收截面“宽带”光谱；σ′i（λ）即差分吸收截面，表示随波长快速变化的吸收截面“窄带”光谱.

则式（5）可简化为

式中：I′0（λ）为不包含差分吸收时的辐射强度.

最终得到差分的Lambert-Beer定律：

定义D′（λ）为差分光学密度，则由此可计算出吸收气体的浓度.

1.2 FFT滤波法

利用差分吸收光谱技术监测气体，常用的方法是取所测波段内的众多波长点，按照最小二乘法进行拟合反演得到气体浓度［4］.由于实际工作中受到外界温度变化、震动等影响，光谱仪可能出现谱线漂移，这将直接影响其测量结果的准确性，另外实测吸收光谱中包括不同气体与噪声的叠加，气体之间的吸收光谱相互干扰，要排除其他气体干扰而准确测定某一组分浓度较困难，而傅里叶变换考虑的是频域信号，谱线漂移及噪声对其几乎无影响.

观察到SO2和NO2等气体的差分吸收截面具有很强的准周期性，其频域能量集中在少数几个频率点上，而其他气体的差分吸收截面也大多具有这个特征.考虑将其进行傅里叶变换，取少数频率点进行计算，能够有效抑制其他与被测气体有不同频谱特性干扰气体的影响［5］.

2 频谱校正基本原理及应用

谐波信号离散傅里叶变换和频谱分析的频率、幅值和相位都可能存在较大误差，所以需要校正以大幅度减小或消除这个误差，提高分析精度［6］.目前主要有能量法、比值法、相位差法、Zoom-FFT 法以及CZT 法等.

利用差分吸收光谱技术监测气体质量浓度时，由于气体的差分吸收截面经快速傅里叶变换后，能量集中在少数几个频率点上，属于间隔较远的多频率成分，笔者采用比值法进行校正.气体差分吸收的效果是由分子特性引起的，即差分吸收截面与差分光学密度具有相同的频谱特性，所以特征频率点具有相同的分布，对频率校正意义不大；而由于FFT滤波法关心的是变换后的特征频率点对应的幅值信息，故舍弃对相位的校正.

由于实测信号不可能是无穷长度的，只能是确定的一段数据，故采样过程相当于对原始信号加了矩形窗.

离散化矩形窗定义为

窗长归一化后，其主瓣内频谱模函数为

k的取值范围为［-1，1］，当N≫1，1／N→0时，存在下列简化条件：

用f1代替k，为使幅值与时域相符，乘以系数1／N，得到窗长归一化的频谱模函数为

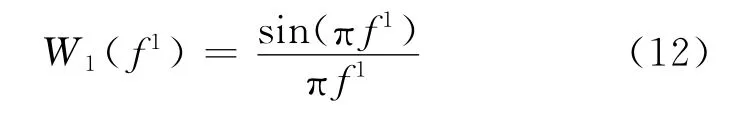
根据式（12）构造如下的校正比值函数：

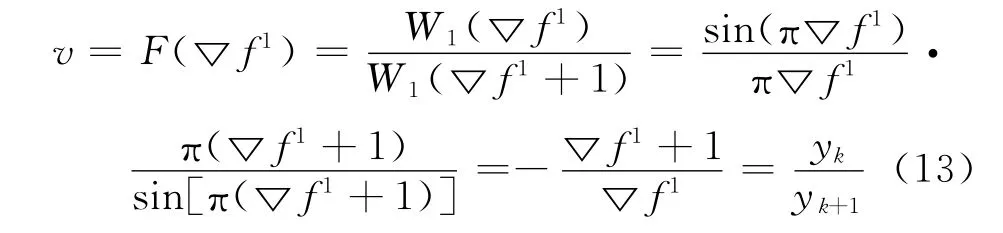
由式（13）可求出归一化的频率校正量：

校正后的幅值为：

对吸收截面σi（λ）进行快速傅里叶变换，得到其频谱，通过设置合适的截止频率，可以降噪并得到差分吸收截面σ′i（λ）；对差分光学密度D′（λ）进行快速傅里叶变换，得到其频谱，通过设置合适的截止频率，降低其噪声.利用前述幅值校正公式（15）可以得到特征频率点对应的幅值A，之后按照FFT 滤波法完成质量浓度反演工作.

3 实验结果与分析

所搭建的实验平台示意图见图1，氙灯光源与光谱仪采用荷兰Avantes公司的产品，并配套相应光纤与软件，吸收池材质为316L 型不锈钢，内部体积为264.6cm3，压力变送器与温控仪等均按照实验要求采购.

图1 实验平台示意图Fig.1 Schematic diagram of the experimental platform

使用质量浓度为568.57mg／m3的SO2标气、1 051.43mg／m3的NO2标气以及高纯N2，配制了不同质量浓度的SO2和NO2单组分气体.利用传统的最小二乘法（简称最小二乘法）、FFT 滤波法与校正FFT 滤波法反演待测气体质量浓度.由于光源不是绝对稳定的，故通过多次测量取平均值来得到实测数据，实验中的平均次数为500，氙灯积分时间为100ms.

对于SO2质量浓度测量实验，首先向抽真空后的吸收池中充入一个大气压的SO2标气，得到568.57mg／m3的配气，记录实验数据，并逐步充入高纯N2，以得到不同质量浓度的配气.选择298～307nm 作为SO2质量浓度反演波段，SO2吸收截面通过568.57mg／m3的配气计算得到.

对于NO2质量浓度测量实验，其步骤与SO2质量浓度测量实验基本相同，不同之处在于所配制的气体质量浓度.选择217～227nm 作为反演波段，SO2吸收截面通过1 051.43mg／m3的配气计算得到.实验结果见表1和表2，3种算法的误差对比见图2和图3.

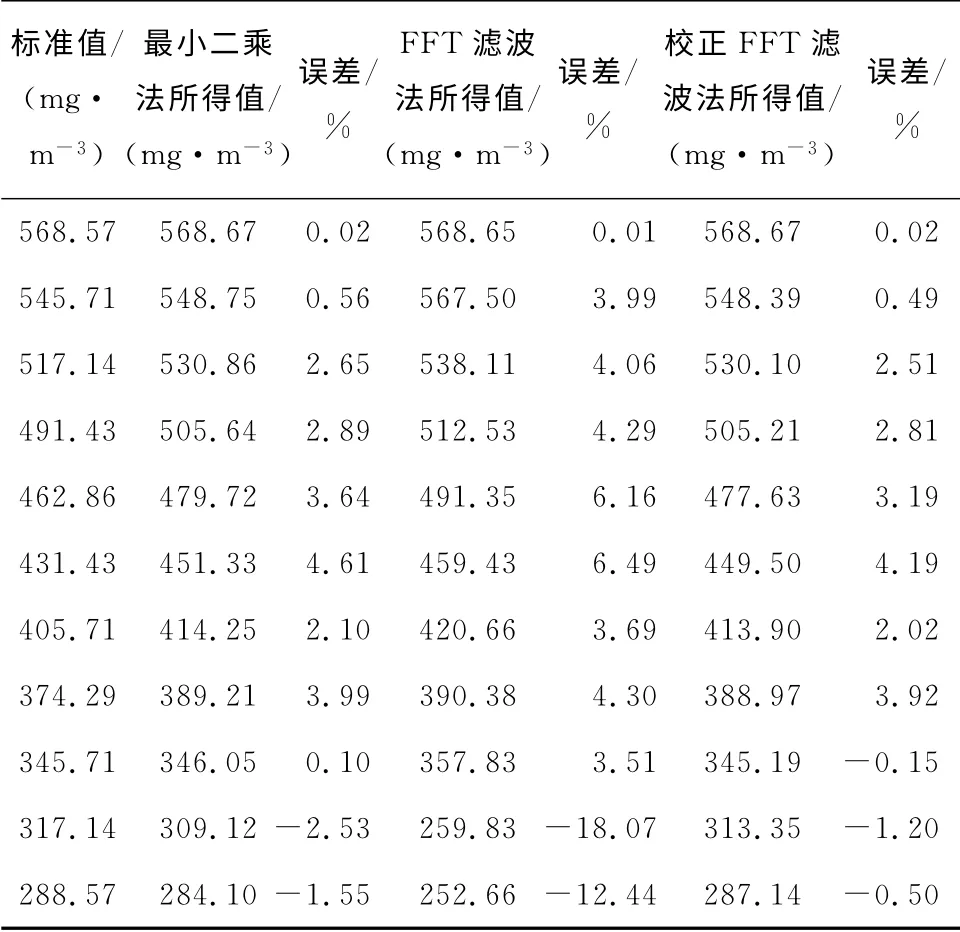
表1 3种反演算法所得SO2 质量浓度的比较Tab.1 Comparison of SO2 mass concentration among three inverse algorithms

由表1与图2可知，在所选择的298～307nm波段，最小二乘法与校正FFT 滤波法的误差较接近，且均小于5%，在国家标准允许偏差范围内.整体而言，校正FFT 滤波法误差比最小二乘法误差小，对于某几个数据点，校正FFT 滤波法误差明显小于最小二乘法.而FFT 滤波法的误差普遍超过另2种方法，最高达18.07%.

分析可知，最小二乘法与校正FFT滤波法均可取得不错的效果，就整体而言，校正FFT 滤波法优于最小二乘法，其反演效果也明显优于FFT滤波法.

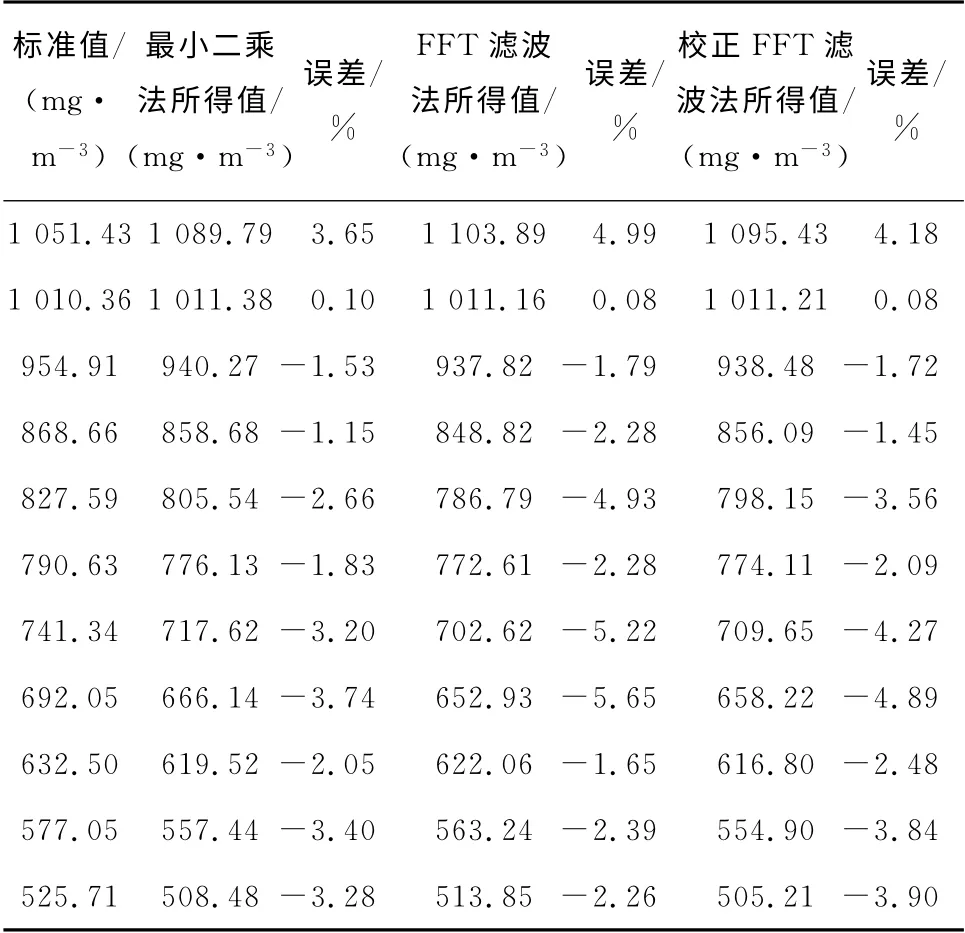
表2 3种反演算法所得NO2 质量浓度的比较Tab.2 Comparison of NO2 mass concentration among three inverse algorithms

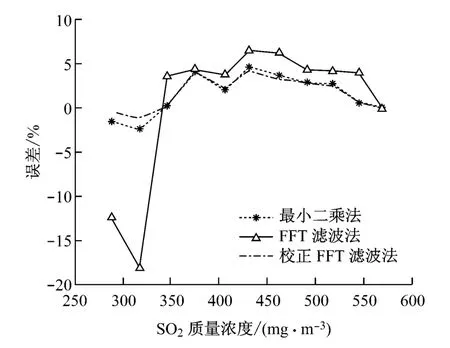
图2 3种反演算法所得SO2 质量浓度的误差对比Fig.2 Error comparison of SO2 mass concentration among three inverse algorithms

图3 3种反演算法所得NO2 质量浓度的误差对比Fig.3 Error comparison of NO2 mass concentration among three inverse algorithms

由表2与图3可知，在所选择的217～227nm波段，最小二乘法与校正FFT 滤波法的误差均小于5%，在允许偏差范围内.整体上，FFT 滤波法与校正FFT 滤波法的误差均比最小二乘法稍大，这主要是因为：虽然选取波长间隔为10nm，与SO2接近，但在相应波段内，NO2包含的完整波的数量较SO2少，所以FFT 滤波法与校正FFT 滤波法反演NO2质量浓度效果不如SO2.分析可知，最小二乘法与校正FFT 滤波法均能取得不错的效果，这与上述SO2质量浓度测量实验结论是一致的，但从整体来看，最小二乘法的效果是最好的，这与SO2质量浓度测量实验略有不同.且校正FFT 滤波法在整体上优于FFT 滤波法.

图4 模拟谱线漂移1个波长时3种反演算法所得SO2 质量浓度误差对比Fig.4 Error comparison of SO2 mass concentration among three inverse algorithms for a drift of one wavelength

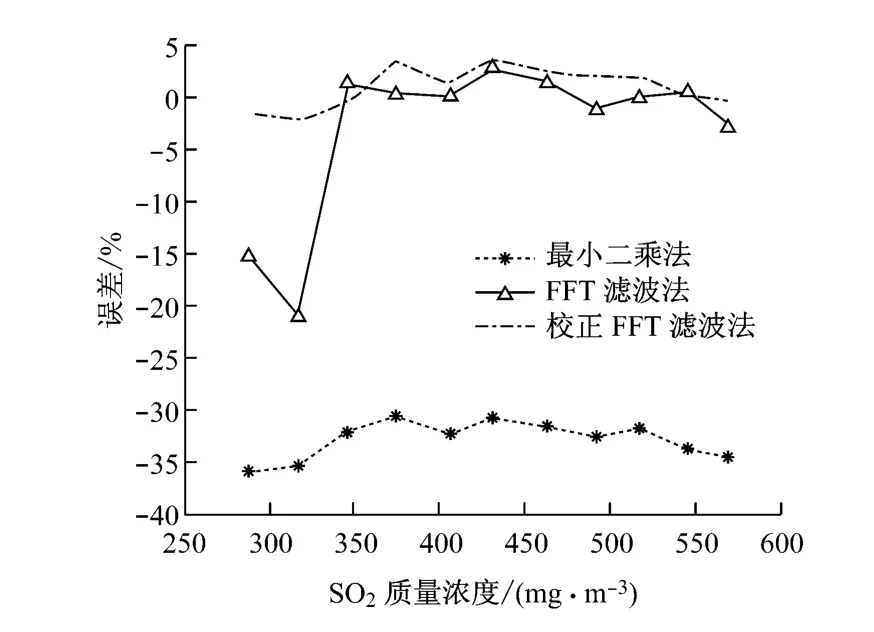
图5 模拟谱线漂移2个波长时3种反演算法所得SO2 质量浓度误差对比Fig.5 Error comparison of SO2 mass concentration among three inverse algorithms for a drift of two wavelengths

考虑到实际检测过程中经常出现光谱谱线漂移的情况，对上述实验所测光谱数据向长波长方向分别进行1个和2个波长的移位（红移），以模拟实际可能出现的状况.笔者模拟了3种算法反演谱线漂移的SO2质量浓度，误差对比结果示于图4和图5，模拟谱线漂移2 个波长时3 种反演算法所得SO2质量浓度误差的比较见表3.由图4和图5可知，当漂移1个波长时最小二乘法误差较大，校正FFT 滤波法误差较小，均在5%以内；当漂移2 个波长时，最小二乘法误差均在30%以上，FFT 滤波法最大误差也达到21.03%，而校正FFT 滤波法的误差均在4%以内，符合国标要求.最小二乘法在谱线漂移的情况下会产生较大误差，而校正FFT 滤波法误差最小，谱线漂移对其几乎无影响，FFT 滤波法的反演效果介于两者之间.

这是因为：最小二乘法利用相应波长点的差分光学密度与差分吸收截面进行拟合来反演质量浓度，若有谱线漂移的情况出现，则某一波长点的差分光学密度与差分吸收截面不会相互对应，故拟合出的质量浓度值会出现较大偏差；而傅里叶变换考虑的是数据在频域内的能量，即幅值A，当谱线漂移时，进行变换的同样是这一组数据，只不过波长发生了移位，但变换至频域时由于不考虑波长信息，频谱图不变，即差分光学密度与差分吸收截面在特征频率点的对应关系并没有改变，故谱线漂移对其几乎无影响.

表3 模拟谱线漂移2个波长时3种反演算法所得SO2质量浓度误差的比较Tab.3 Error comparison of SO2 mass concentration among 3 inversion algorithms for a drift of two wavelengths

4 结 论

利用搭建的实验平台对单组分SO2、NO2气体进行实验，配制了不同质量浓度的气体，并模拟了实际可能出现的谱线漂移情况.实验结果表明：对于单组分SO2气体，校正FFT 滤波法能取得较优于传统最小二乘法的效果，且误差明显小于FFT 滤波法；对于单组分NO2气体，传统的最小二乘法效果最好，整体而言，校正FFT 滤波法优于FFT 滤波法.模拟谱线漂移的实验结果表明，校正FFT 滤波法能有效排除谱线漂移的干扰，取得明显优于传统最小二乘法的效果.但不同气体的频谱特征不尽相同，如何从混合气体中提取某一种待测气体的质量浓度信息还需做进一步的工作.

［1］STUTZ J，PLATT U.Numerical analysis and estimation of the statistical error of differential optical absorption spectroscopy measurements with least-squares methods［J］.Appl Optics，1996，35（30）：6041-6053.

［2］郑海明，蔡小舒.基于差分吸收光谱法的烟气排放监测实验［J］.环境工程，2007，25（1）：66-68. ZHENG Haiming，CAI Xiaoshu.Experiment on flue gas continuous emission monitoring based on differential optical absorption spectroscopy［J］.Environmental Engineering，2007，25（1）：66-68.

［3］王姗姗，蔡小舒，苏明旭.强烟尘水滴干扰下DOAS法在线测量NO 质量浓度的研究［J］.动力工程学报，2011，31（11）：875-881. WANG Shanshan，CAI Xiaoshu，SU Mingxu.DOAS method for on-line measurement of NO mass concentration interfered by high density of dust and water droplets［J］.Journal of Chinese Society of Power Engineering，2011，31（11）：875-881.

［4］邵理堂，汤光华，许传龙，等.短光程下差分吸收光谱法测量低浓度污染气体的反演算法［J］.中国电机工程学报，2008，28（23）：65-70. SHAO Litang，TANG Guanghua，XU Chuanlong，et al.Inversion algorithm of differential optical absorption spectroscopy to measurement low mass concentration of polluted gas under short light path［J］.Proceedings of the CSEE，2008，28（23）：65-70.

［5］毛万朋，蔡小舒，程智海，等.傅里叶变换滤波——差分吸收光谱法在烟气SO2在线监测中的应用研究［J］.工程热物理学报，2004，25（增刊）：205-208. MAO Wanpeng，CAI Xiaoshu，CHENG Zhihai，etal.Fourier transform filtering—the application of differential optical absorption spectroscopy in the on-line SO2monitoring system［J］.Journal of Engineering Thermophysics，2004，25（s）：205-208.

［6］丁康，谢明，杨志坚.离散频谱分析校正理论与技术［M］.北京：科学出版社，2008：100-102.