图着色问题的逆序蚁群算法研究

张 丽， 丁晓东

（1.上海理工大学管理学院，上海 200093；2.上海工程技术大学航空运输学院，上海 201620）

图着色问题的逆序蚁群算法研究

张 丽1，2， 丁晓东1，2

（1.上海理工大学管理学院，上海 200093；2.上海工程技术大学航空运输学院，上海 201620）

针对经典的图着色问题，依据传统图着色算法中逆序图着色的着色思想，结合蚁群算法的搜索机制，给出了逆序蚁群着色算法.根据着色进度和未着色点的相邻点度数随机动态逆序选择新的着色点，使得算法具有较强的搜索全局最优解的能力.利用计算机生产大量随机图作为测试实例，对比逆序着色算法和逆序蚁群算法，实验结果说明逆序蚁群着色算法提高了求解质量，加快了收敛速度，证明了其优良特性.同时算法效率的提高，也保证了该算法可适用于较大规模的着色问题求解.此外，还进行了一系列对比试验，得出了关键参数的合理取值范围.

图着色问题；逆序着色算法；逆序蚁群着色算法

图着色问题（graph coloring problem，GCP）是现代图论中重要课题之一，在存储分配、电路布线、机场停机位分配等问题中也有广泛的应用.图着色的内容包括点着色、边着色、组合地图的面着色等，边着色和面着色都可转化为点着色问题.

图着色问题是组合优化中一个很活跃的课题，国内外研究人员进行过许多研究，并取得了一系列成果.在理论方面，对“四色猜想”和“五色定理”的证明相继引出许多重要结果，另外还有有关色多项式和一些根据子图特征分析着色数上界的结论［1-2］.

后来，从实用角度出发，更多的研究集中在算法设计而不再是理论证明上.早期的算法研究主要是如基于布尔代数运算的着色算法和基于深度优先检索的回溯算法等经典方法，但由于图着色问题属于NP难题，经典图着色算法随着图的规模增大，计算量将以指数速度增加到不可接受的地步.之后一些近似算法相继推出，如逆序标号算法和贪心算法等启发式算法［3-4］.

自从蚁群算法在著名的旅行商问题和工件排序问题上取得成效以来，已陆续渗透到其它组合优化问题领域中，并在许多方面表现出相当好的性能.目前，蚁群算法在着色问题方面的应用较少.

1 问题描述

已知G=（V，E），其中，｜V｜=n；｜E｜=m；且G为无自环的无向图.

对图G点着色，是指将它的每个顶点涂上一种颜色，使得任何相邻的顶点都涂上不同的颜色.若用k种颜色能够对G的顶点进行一种着色，就称G是k-点可着色的.若G是k-点可着色的，但不是（k-1）-点可着色的，就简称G是k-色图，称k 为G的色数［5］.

问题的数学模型可写成

2 逆序蚁群算法

2.1 逆序着色算法

逆序着色算法是对经典图着色算法——Welch Powell着色法的改进，Welch Powell着色法的原理是将图G中的结点按度数递减的次序进行排列，用第一种颜色，对第一点着色，并按排列次序对与前面结点不相邻的每一点着同样的颜色.然后用第二种颜色对尚未着色的点重复前一步，直到所有的点都着上颜色为止.

逆序着色算法的步骤为：

步骤1 取顶点v1，deg（v1）=max｛deg（vi）｜vi∈V｝，即选择度数最大的顶点，令c（v1）=1，M1=｛v1｝，V1=V＼｛v1｝.

步骤2 取v2∈V1，并且与M1中的顶点邻接的度数为最大，令c（v2）=2，M2=｛v1，v2｝，V2=V1＼｛v2｝.

步骤3 取v3∈V2，并且与M2中的顶点邻接的度数为最大，令

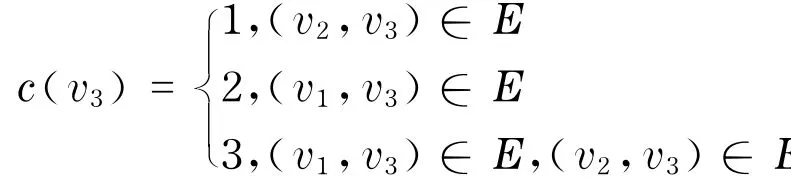
步骤4 一般地，设Mk=｛v1，v2，…，vk，｜vj∈V，j=1，2，…，k｝，Vk=Vk-1＼｛vk｝；若Vk+1=φ，则转步骤5；否则，若vk-1∈Vk，并且与Mk中的顶点邻接的度数为最大且唯一，令c（vk）=j （j为可以使用的最小数颜色）.

步骤5 C（G）=max（c（vi），vi∈E）

2.2 逆序蚁群着色算法

图着色问题不像TSP问题有现成的测试库，一般而言，图着色问题的算法测试常用随机生成图来检验相关算法的正确性和效率.一个随机图Gn，pE表示有n个顶点，点与点之间以概率pE存在关联边，并且这些边是否存在是相互独立的.这类随机图已经用各种算法做过大量测试，尤其是当pE=0.5时的情况更有很多测试结果，得到了有意义的结论.

基本蚁群算法主要用于寻路问题［6-10］，下面借鉴其思路对逆序着色法进行改进，蚂蚁在寻路过程中增加了着色任务，着色点的选择和颜色的选择是算法设计关键.改进后的算法可用于规模较大的问题，特别是大型的随机图Gn，pE着色，可以继承传统图着色算法的搜索机制，并同时获得蚁群算法能够跳出局部解的优良特性.

其算法流程为：

步骤1 参数初始化.

蚂蚁总数A赋值，轨迹信息素矩阵T为全1矩阵，当前最优着色数C*（G）初值为n，着色数C（G）←1，1号色着色点集C1（G）=φ，1号色不可着色点集（G）=φ；k←1，未着色点集Vc=φ.

步骤2 第a个蚂蚁开始着色.

选择第一个着色点vi，deg（v1）=max｛deg（vi）｜vi∈V｝（第一着色点亦可使用其它选择方案，例如随机选择）.

步骤3 为vi着色.

步骤4 着色进度判断.

式中，ηij为vj点饱和度，表示vj与Vc中的点相邻度数，与未着色点相邻越多的点被选择的几率越大；τij=T（i，j）；α表示信息素轨迹的相对重要性；β表示路径能见度的相对重要性；而ρ为信息素蒸发系数.选择最大转移概率对应的vj，转步骤3.

步骤6 记录蚂蚁a的着色结果.

3 计算实验与分析

3.1 算法效率比较

下面就用随机图Gn，pE来检验逆序蚁群着色算法的求解效率.

在测试中，取ρ=0.5，α=β=2，表1中列出了其它实验参数.

从表2显示的结果可以看出逆序蚁群算法在算法结果上整体优于逆序着色算法，点数和关联边增加的时候尤其明显.

表1 逆序蚁群着色算法的其它实验参数Tab.1 Experimental parameters of ant coloring algorithm

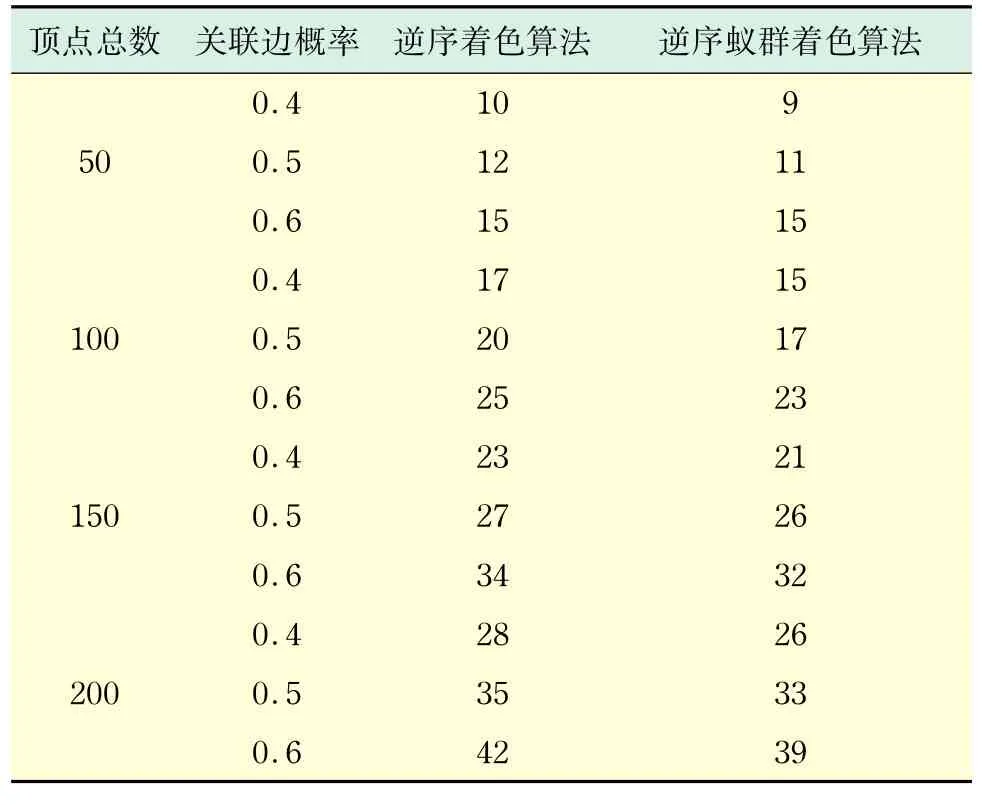
表2 两种算法的求解结果比较Tab.2 Results comparision between the two coloring algorithms

3.2 算法参数的选择

3．2．1 参数α与β

为探索参数信息素轨迹的相对重要性α和路径能见度的相对重要性β的设置规律，选择较优的参数组合，下面使用随机图G100，0.5作为算例测试.α 和β分别取1，2，3，4进行组合，蒸发系数取值仍然取0.5.除α和β同时取值为1的情况，由于硬件环境的局限，其它α和β的组合对每种算法都进行了4次实验，实验的平均结果见表3.

表3 不同重要度参数组合下的算法试测结果Tab.3 Different combinations of parameters_____

由上述测试结果可以看出，当α=1，β=2时，这种组合的平均求解质量较高.

3．2．2 蒸发系数ρ

仍以随机图G100，0.5为例，蚂蚁总数取50，依据上面一组实验结论α和β都取为1，在信息素蒸发系数变动时，可得到不同蚂蚁着色算法的着色结果，如图1所示.

图1 不同蒸发系数对算法的影响Fig.1 Effect of different evaporation coefficients

根据以上实验结果可以推断出ρ在（0.5，0.7）之间时，逆序蚁群着色算法求解效果较好.

3．2．3 蚁群规模

在前面的实验过程中还可以观察到，当蚁群规模达到50时，即使关联边的产生概率不同，逆序蚁群算法也都基本达到了可能实现的最好结果.蚁群规模继续增加时，收敛速度已经变得缓慢，因而可以选择50只蚂蚁来执行着色任务.

4 结束语

图着色问题是经典的分配型组合优化问题，且属于NP难题.传统的图着色算法时间复杂度较高，而随机蚂蚁着色算法搜索机制又比较盲目.本文将传统算法的选择策略融合在其中，设计的逆序蚁群着色算法在实验中验证了其优良的特性，即降低了逆序着色算法的时间复杂度，又提高了求解结果的质量.

算法的时间复杂度为O（A*n2）.经验结果是，当n＞50时，A取50即可.值得注意的是，由于图着色问题的本身的复杂性，算法的时间和空间复杂度仍高于基本的寻路蚁群算法.

在机场停机位分配、工件排序等着色问题的实际应用领域，逆序蚁群着色算法需要有针对性的改进才可以应用［11-12］.

［1］ Edwards K.The complexity of coloring problems on dense graphs［J］.Theoretical Computer Science，1986，43（2／3）：337-343.

［2］ Held S，Cook W，Sewell E C.Maximum-weight stable sets and safe lower bounds for graph coloring［J］. Mathematical Programming Computation，2012，4（4）：361-381.

［3］ 卢开澄，卢华明.图论及其应用［M］.北京：清华大学出版社，1995.

［4］ 肖位枢.图论及其算法［M］.北京：航空工业出版社，1993.

［5］ Porumbel D C.Heuristic algorithms and learning techniques：applications to the graph coloring problem ［J］.4OR，2012，10（4）：393-394.

［6］ Dorigo M，Maniezzo V，Colorni A.Ant system：optimization by a colony of cooperating agents［J］. IEEE Transactions on Systems，Man and Cybernetics，1996，26（1）：29-41.

［7］ 李煜，马良.用量子蚁群算法求解大规模旅行商问题［J］.上海理工大学学报，2012，34（4）：355-358.

［8］ Walter J.A graph-based ant system and its convergence［J］.Future Generation Computer Systems，2000，16（8）：873-888.

［9］ Bui T N，Nguyen T V H，Patel C M，et al.An ant-based algorithm for coloring graphs［J］.Discrete Applied Mathematics，2008，156（2）：190-200.

［10］ 廖飞雄，马良.图着色问题的启发式搜索蚂蚁算法［J］.计算机工程，2007，33（16）：191-192.

［11］ 王欣盛，马良.工件排序的改进蚁群算法优化［J］.上海理工大学学报，2011，33（4）：362-366.

［12］ 任上，秦江涛.基于着色Petri网实现A星算法的生产调度优化研究［J］.上海理工大学学报，2013，35（5）：463-474.

（编辑：董 伟）

Reverse Order Ant Colony Algorithm for Graph Coloring Problem

ZHANGLi1，2， DINGXiao-dong1，2
（1.School of Management，University of Shanghai for Science and Technology，Shanghai 200093，China；2.Air Transport Department，Shanghai University of Engineering Science，Shanghai 201620，China）

Based on the traditional reverse ordering graph coloring algorithm and combining with searching mechanism of ant algorithm，a reverse order ant coloy coloring algorithm was proposed to resolve graph coloring problems.In the algorithm according to the color progress and the adjacent points degree，the dynamic reverse transferring color sequence can give the algorithm strong ability to search the global optimal solution.A large number of random graph coloring experiments show the advantages of the new algorithm.The algorithm can improve the quality of solution and make the convergence faster.An improvement of the efficiency of the algorithm also ensures that it can be applied to solve large-scale coloring problems.In addition，through series of computer test，reasonable value ranges of key parameters were validated.

graph coloring problem；reverse order coloring algorithm；reverse order ant colony coloring algorithm

TP 18文献标示码：A

1007-6735（2014）05-0483-04

10.13255／j.cnki.jusst.2014.05.014

2013-09-11

上海市一流学科建设资助项目（S1201YLXK）；上海市教委科研创新资助项目（12YS129）

张 丽（1980-），女，博士研究生.研究方向：智能优化.E-mail：zhanglisues＠163.com

丁晓东（1963-），男，教授.研究方向：不确定系统分析与优化.E-mail：xdding＠usst.edu.com