区间直觉梯形模糊几何Bonfer roni平均算子及其应用

周晓辉， 姚 俭

（上海理工大学管理学院，上海 200093）

区间直觉梯形模糊几何Bonfer roni平均算子及其应用

周晓辉， 姚 俭

（上海理工大学管理学院，上海 200093）

研究了决策信息为区间直觉梯形模糊数且属性间存在相互关联的多属性群决策问题，提出一种基于区间直觉梯形模糊几何加权Bonferroni平均算子的决策方法.基于区间梯形直觉模糊数的运算法则和几何Bonferroni平均算子，定义了区间直觉梯形模糊几何Bonferroni平均算子及其加权算子.给出了这些算子的一些性质，建立基于区间直觉梯形模糊几何加权Bonferroni平均算子的多属性群决策模型.最后，将该方法应用在供应商选择的群决策问题中，结果表明了该方法的有效性与可行性.

区间直觉梯形模糊数；几何Bonferroni平均算子；多属性群决策

Key words：interval-valued intuitionistic trapezoidal fuzzy number；geometric weighted Bonferroni means operator；multi-attribute group decision making

自Atanassov提出直觉模糊集［1］（intuitionistic fuzzy sets，IFS）以来，因IFS综合考虑隶属度、非隶属度和犹豫度三方面的信息，能更加细腻地描述和刻画客观世界的模糊性本质，众多学者对IFS进行了深入研究.目前关于IFS的拓展形式主要有区间直觉模糊集（interval-valued intuitionistic fuzzy sets，IVIFS）［2-4］、三角直觉模糊数（triangular intuitionistic fuzzy numbers，TIFN）［5-6］、直觉梯形模糊数（intuitionistic trapezoidal fuzzy numbers，ITFN）和区间直觉梯形模糊数（interval-valued intuitionistic trapezoidal fuzzy numbers，IVITFN）［7］.王坚强［7］于2008年首次提出了IVITFN的概念，但与其相关的研究并不多见.因IVITFN的隶属函数和非隶属函数用区间数描述，在刻画客观世界的模糊性本质方面比IFS，IVIFS，ITFN 和TIFN更为精细和准确，因而引起了众多学者的关注.万树平［8］探讨了IVITFN的运算法则，定义其得分函数和精确函数，给出了IVITFN的排序方法，定义了IVITFN的加权算术平均（IVITFNWAA）和加权几何平均算子（IVITFNWGA），并将其应用于多属性群决策（MAGDM）领域.Wu等［9］研究了IVITFN的加权几何算子（IVITFNWG）、有序加权几何算子（IVITFNOWG）和混合几何算子（IVITFNHG），并给出MAGDM方法.汪新凡等［10］定义了新的IVITFN加法运算法则，结合IVITFN的期望值给出了新的IVITFN加权算术平均（IVITFNWAA）算子、有序加权平均（IVITFNOWA）算子和混合集成（IVITFNHA）算子.

上述研究的IVITFN集成算子仅考虑了属性间相互独立的情况，实际决策中，不同属性间会存在不同程度的联系，如互补、冗余、偏好关系等.有关属性间具有相互关联的IVITFN集成算子却不曾见到报道.基于Bonferroni提出的BM算子［11］能够很好地捕获输入变量之间的相互关联情况，其可以将多个输入变量集结为一个输入变量，是一种介于最大和最小之间的集成算子.Xu等［12］在直觉模糊环境下拓展了BM算子进行IFS的信息集成，另外将BM算子与IVIFS结合，提出了IVIFBM算子，研究了相关的性质，并应用于MAGDM领域［13］.Dutta等［14］将ITFN和BM算子结合，提出了直觉梯形模糊Bonferroni（ITFBM）算子和广义直觉梯形模糊Bonferroni（GITFBM）算子.Xia等［15］研究了几何Bonferroni平均（GBM）算子，在直觉模糊环境下将IFS与GBM算子结合，提出了直觉模糊几何Bonferroni平均（IFGBM）算子和直觉模糊几何加权Bonferroni平均（IFGWBM）算子，同时研究了其性质，并通过MADGM算例验证了IFGWBM算子的有效性和实用性.

基于以上分析，本文将IVITFN与GBM算子相结合，提出IVITFGBM算子和IVITFGWBM算子，同时研究它们的一些性质.最后给出一种基于IVITFGWBM算子的MAGDM方法.

1 基本理论

1.1 IVITFN定义

定义1［7-9］设α～实数集上的一个IVITFN的区间值隶属函数为

图1 区间直觉梯形模糊数Fig.1 Interval-valued intuitionistic trapezoidal fuzzy number

1.2 IVITFN的运算法则

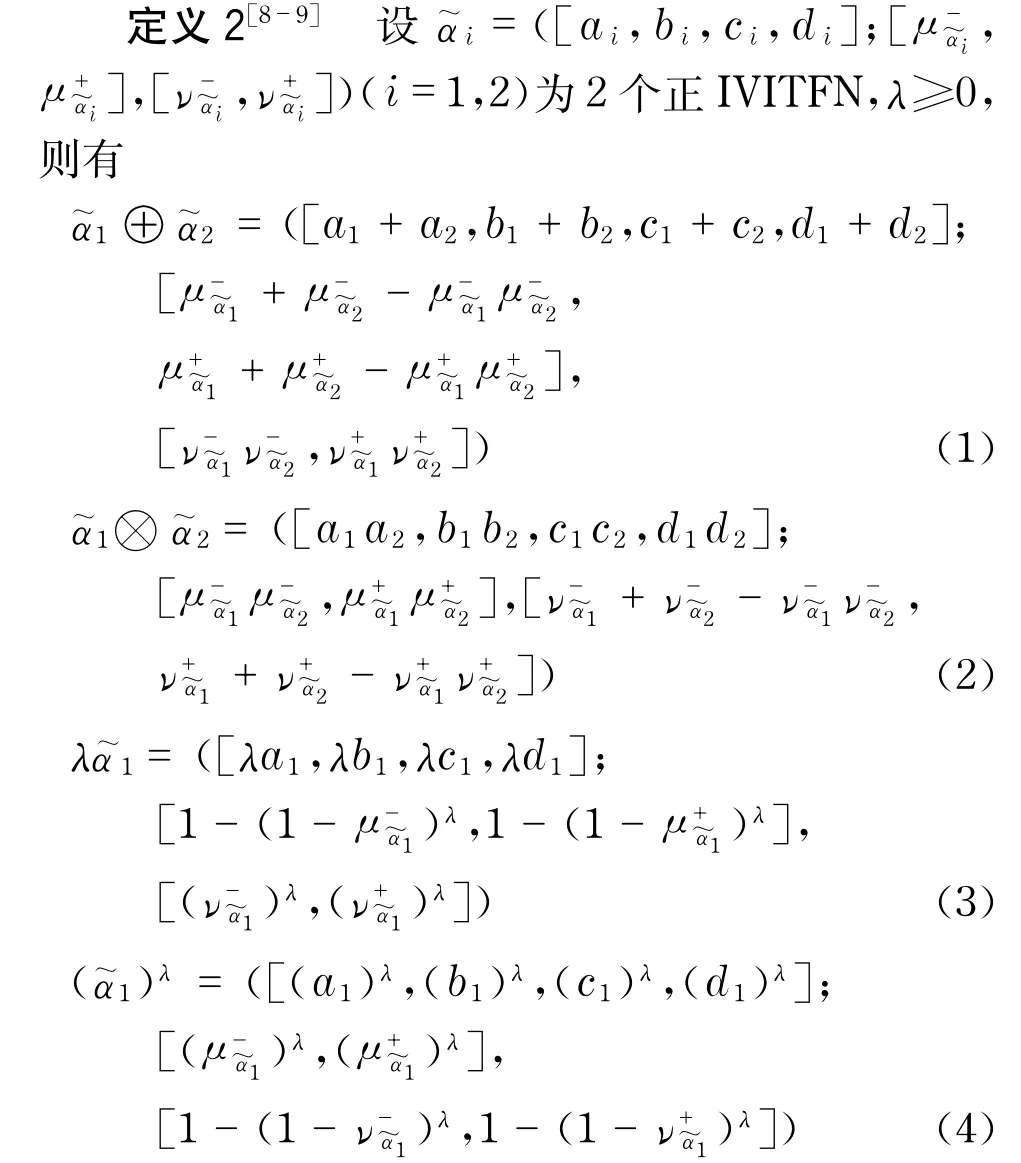
1.3 IVITFN的排序方法

1.4 GBM算子

定义4［15］设p，q＞0，且非负实数集合｛a1，a2，…，an｝满足

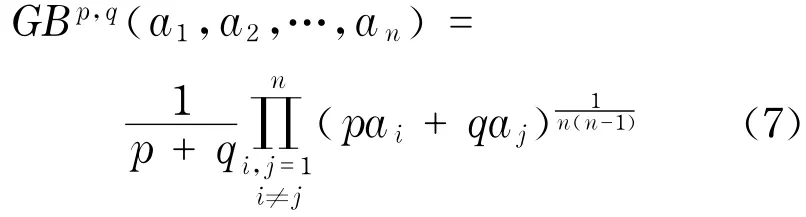
则称函数GBp，q为GBM算子.

为处理决策信息以IVITFN给出的MAGMD问题，结合GBM算子给出IVITFGBM算子.

1.5 IVITFGBM算子

1.6 IVITFGWBM算子

基于以上研究知，IVITFGBM算子考虑了属性间关联性，是一种IVITFN集成的新方法，但是在实际应用中，属性具有不同的重要程度，为此，提出IVITFGWBM算子.

定理6的证明类似定理1，限于篇幅，证明过程略.

2 基于IVITFGWBM算子的MAGDM方法

步骤1 设决策者dk给出方案Ai在属性Cj下的评价值为IVITFN，从而得到决策矩阵为D（k）= （α）n×t.

步骤2 利用IVITFGWBM算子，对m位决策专家给出的决策矩阵进行信息集成，综合专家权重，得到方案Ai（i=1，2，…，t）的总体评价值.

步骤3 计算得分函数值与精确函数值，根据IVITFN排序方法对方案进行优劣排序，进而得到最佳方案. wj=1.具体决策步骤如下：

3 实例分析

某食品公司拟从3个供应商（A1，A2，A3）中选择合适的合作伙伴，故针对每个供应商的4个属性进行了评估，4个属性分别为：产品质量C1；技术能力C2；污染控制C3；环境管理C4.属性的权重向量为w=［0.25，0.2，0.35，0.2］T，有3位决策专家d1，d2，d3分别对这A1，A2，A3根据上述的4个属性进行满意度测评，如表1～3所示.给出的测评值均为IVITFN，其中3位决策者的权重向量为ω= ［0.2，0.3，0.5］T.采用本文提出来的方法对供应商进行选择.

表1 决策者d1给出的决策矩阵Tab.1 Decision matrix from decision maker d1

表2 决策者d2给出的决策矩阵Tab.2 Decision_ matrix from decision maker d2

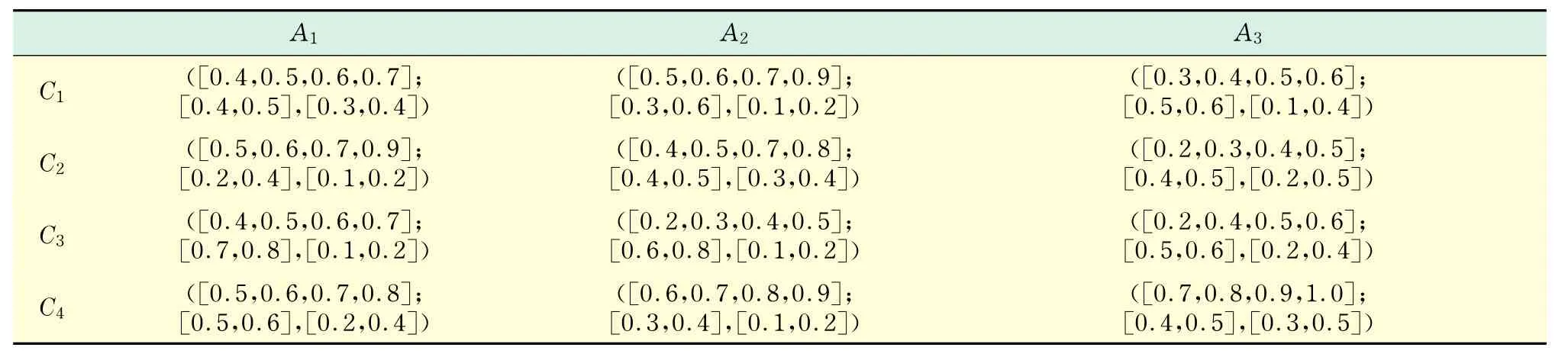
表3 决策者d3给出的决策矩阵Tab.3 Decision matrix from decision maker d3

步骤1 本文研究p=1，q=1的情况，由式（22）算出各个决策者对每个供应商的测评值如下：

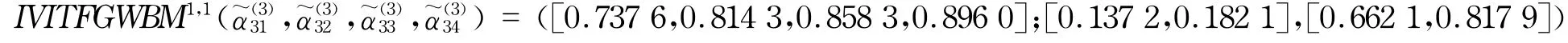
步骤2 考虑到决策者的权重，通过加权得到每个供应商的测评结果如表4所示.

表4 测评结果、得分函数值和精确函数值Tab.4 Evaluation results，scoring function values and precise function value

步骤3 由式（5）、式（6）计算得分函数值和精确函数值如表5所示，然后根据IVITFN排序方法对供应商进行优劣排序为A1＞A3＞A2.因此，最优的供应商为A1.

对比分析文献［8］，运用IVITFWAA算子和IVITFWGA算子的结果如表5所示.

表5 IVITFWAA算子和IVITFWGA算子集成结果Tab.5 Integration results of IVITFWAA operator and IVITFWGA operator

由表5知，通过IVITFWAA算子和IVITFWGA算子得到供应商的优劣排序均为A1＞A2＞A3.最优的供应商为A1，而A2，A3的优劣排序与IVITFGWBM算子的不同，主要因为本文提出的IVITFGWBM算子考虑了属性间的关联性.

4 结束语

实际生活中的MAGDM问题，决策属性之间往往存在不同程度上的相互关联［17-19］.针对现有IVITF信息集结算子存在的不足，结合GBM算子，研究了IVITFGBM算子和IVITFGWBM算子，并研究了IVITFGBM算子的一些性质，最后将IVITFGWBM算子应用在MAGDM中.算例结果表明了该算子的有效性和正确性.与传统方法对比，该方法考虑了决策属性间的关联性，使决策分析更接近决策问题的实际情况，决策结果更加合理，为解决MAGDM问题提供了新思路.

［1］ Atanassov K T.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20（1）：87-96.

［2］ Xu ZS，Yager R R.Intuitionistic and interval-valued intutionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group［J］.Fuzzy Optimization Decision Making，2009，8（2）：123-139.

［3］ Li D F.TOPSIS-based nonlinear-programming methodology for multiattribute decision making with interval-valued intuitionistic fuzzy sets［J］.IEEE Trans on Fuzzy Systems，2010，18（2）：299-231.

［4］ 徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用［J］.控制与决策，2007，22（2）：215-219.

［5］ Shu M H，Cheng C H，Chang J R.Using intuitionistic fuzzy sets for fault tree analysis on printed circuit board assembly［J］.Microelectronics Reliability，2006，46（12）：2139-2148.

［6］ Li D F.A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems［J］.Computers and Mathematics with Applications，2010，60（6）：1557-1570.

［7］ 王坚强.模糊多准则决策方法研究综述［J］.控制与决策，2008，23（6）：601-607.

［8］ 万树平.基于区间直觉梯形模糊数的多属性决策方法［J］.控制与决策，2011，26（6）：857-866.

［9］ Wu J，Liu Y J.An approach for multiple attribute group decision making problems with interval-valued intuitionistic trapezoidal fuzzy numbers［J］.Computers and Industrial Engineering，2013，66（2）：311-324.

［10］ 汪新凡，杨小娟.基于区间直觉梯形模糊数的群决策方法［J］.湖南工业大学学报，2012，26（3）：1-9.

［11］ Bonferroni C.Sulle medie multiple di potenze［J］. Bolletino dell′UNIONE Matematica Italiana，1950，5 （3／4）：267-270.

［12］ Xu ZS，Yager R R.Intuitionistic fuzzy bonferroni means［J］.IIEEE Trans On Systems，Man，and Cybernetics，Part B：Cybernetics，2011，41（2）：568 -578.

［13］ Xu ZS，Chen Q.A multi-attribute decision-making process based on interval-valued intuitionistic fuzzyBonferroni mean［J］.Journal of Systems Engineering and Electronics，2011，20（2）：217-228.

［14］ Dutta B，Guha D.Trapezoidal intuitionistic fuzzy Bonferroni means and its application in multi-attribute decision making［C］∥IEEE International Conference on Fuzzy Systems.Hyderabad：IEEE，2013.

［15］ Xia M M，Xu Z S，Zhu B.Geometric Bonferroni means with their application in multi-criteria decision making ［J］.Knowledge-Based Systems，2013，40（4）：88 -100.

［16］ Xu ZS，Yager R.Some geometric aggregation operators based on intuitionistic fuzzy sets［J］.International Journal of General Systems，2006，35（4）：417-433.

［17］ 彭国樑，姚俭.不确定性供应链风险的模糊综合评判［J］.上海理工大学学报，2010，32（4）：373-377.

［18］ 周晓辉，姚俭，吴天魁.梯形模糊数直觉模糊Bonferroni平均算子及其应用［J］.数学理论与应用，2014，34（1）：71-82.

［19］ 周晓辉，姚俭，吴天魁.基于梯形直觉模糊数的TOPSIS多属性决策方法［J］.上海理工大学学报，2014，36（3）：281-286.

（编辑：丁红艺）

Interval-valued Intuitionistic Trapezoidal Fuzzy Geometric Bonferroni Means and Its Application

ZHOU Xiao-hui， YAOJian
（Business School，University of Shanghai for Science and Technology，Shanghai 200093，China）

For solving multiple attributes group decision-making（MAGDM）problems where attribute values are in the form of interval-valued intuitionistic trapezoidal fuzzy numbers and attributes are associated with each other，an approach was proposed based on interval-valued intuitionistic trapezoidal fuzzy geometric weighted Bonferroni means（IVITFGWBM）operator.The concepts of interval-valued intuitionistic trapezoidal fuzzy numbers were introduced，and intervalvalued intuitionistic trapezoidal fuzzy geometric Bonferroni means（IVITFGBM）operator and IVITFGWBM operator were defined based on operational laws and Bonferroni means operator. Meanwhile，the related properties were analysed，then a model of multi-attribute group decision making was constructed based on IVITFGWBM operator，which was for making decisions combined with sort methods.The approach was further applied in group decision-making problems of supplier selection，and the results show that the developed approach is feasible and effective.

C 934文献标示码：A

1007-6735（2014）05-0461-08

10.13255／j.cnki.jusst.2014.05.010

2013-12-25

周晓辉（1987-），男，硕士研究生.研究方向：系统工程、模糊决策理论与应用.E-mail：zxhhappy521g＠163.com

姚 俭（1960-），男，教授.研究方向：智能控制、模糊系统理论、系统工程.E-mail：yaojian＠usst.edu.cn