基于频率响应的悬臂工字型钢梁的结构损伤分析

周 奎， 宁娜娜， 林 杰

（上海理工大学环境与建筑学院，上海 200093）

基于频率响应的悬臂工字型钢梁的结构损伤分析

周 奎， 宁娜娜， 林 杰

（上海理工大学环境与建筑学院，上海 200093）

基于结构动力学的基本理论，分析了悬臂工字型钢梁的振动模态特性，推导出结构损伤因子与损伤位置和损伤程度的函数关系.根据结构频率响应，运用频率平方变化比的方法进行结构损伤的初步检测与评估.应用ANSYS有限元分析软件对一悬臂工字型钢梁在11种工况下进行模拟计算，采用单元刚度折减来模拟结构损伤，并对工字型钢梁进行模型实验.

结构损伤；频率响应；悬臂工字型钢梁；有限元分析；损伤检测

随着我国钢铁工业和钢结构技术的迅速发展，钢结构建筑在现代工程结构中得到了较为广泛的应用，悬臂薄壁构件以其强度高、材料省、重量轻的特点已成为钢结构建筑的主要受力构件.而结构一旦投入使用，就会在环境侵蚀与荷载效应等的耦合作用下产生不同程度的损伤，其维护及健康监测就显得尤为重要［1］.结构的损伤必将影响结构的振动特性，通过研究结构的振动特性参数就可预测结构损伤的位置和程度［2］.结构的频率响应能够直接通过实验测得，这类数据比一般的模态参数包含更丰富的信息.Park等［3］和Schulz等［4］运用交叉谱密度函数及频率响应函数进行了损伤位置的识别.国内郑明刚等［5］也运用频响函数的曲率改变进行了单点损伤识别研究.

在研究结构的损伤之前，一般先用有限元分析软件进行理论计算和模拟，这样可以减少实际工作量，降低成本.因此，以有限元分析软件的计算结果作为理论指导，对实现结构损伤的识别具有指导性作用.对于构件较少、刚度较小的结构，本文选择基于频率平方变化比的结构损伤分析方法，并运用ANSYS有限元分析软件对悬臂工字型钢梁进行计算和分析，模拟了悬臂工字型钢梁在不同工况下的频率响应，并对结果进行对比和分析［6］.

1 基本方法

结构的物理参数变化必将引起结构模态参数的变化，而不同位置不同程度的损伤对各阶模态的影响不同，正是运用这种变化差异来初步确定结构的损伤位置［7］.对于一个多自由度的结构系统，根据结构动力学理论，其振动方程为

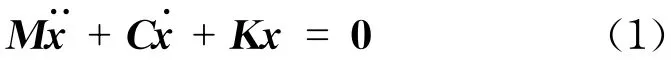
式中，M为整体质量矩阵；C为阻尼系数矩阵；K为整体刚度矩阵；x，x·，x··分别为位移向量、速度向量和加速向量.

忽略阻尼影响，其振动特征方程可以表示为

式中，ω为结构自振频率；φ为结构正交化振型.

从式（2）中可以看出，结构的固有频率和振型主要与结构的质量和刚度有关，因而当结构发生损伤时，质量和刚度均会发生变化，则结构发生损伤后的振动特征方程可表示为

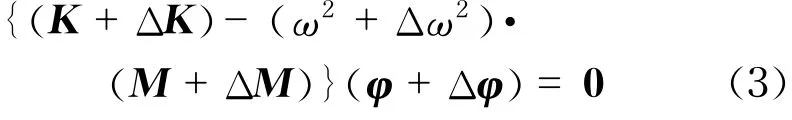
在实际结构中，损伤大多由裂纹和腐蚀引起，所以，质量的变化ΔM很小，可以忽略不计，即ΔM≈0，并将式（3）展开，忽略频率的平方项，则有频率平方的变化量

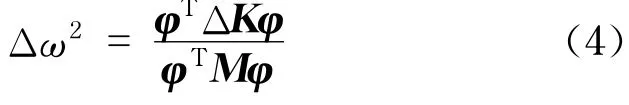
对于第i阶振型，由式（4），有

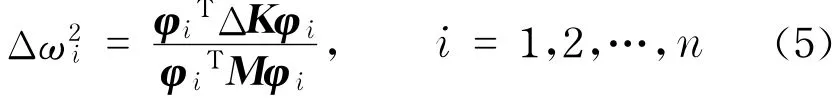
式（5）即为结构损伤方程，当只有第n个单元发生损伤时

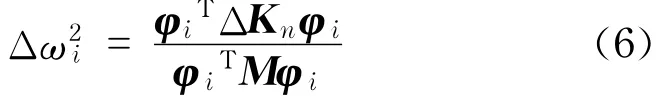
频率的变化可以表示为单元损伤程度和损伤位置的函数，即

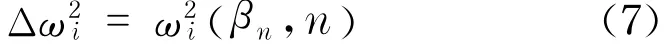
式中，βn为标量，表示单元损伤程度.

由ΔKn=βnKn，结合式（6）和式（7），则有

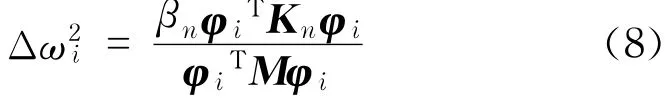
由式（8）可以看出，结构的频率变化是结构损伤程度和损伤位置的函数.现取任意两阶振型对应的频率平方的变化量之比

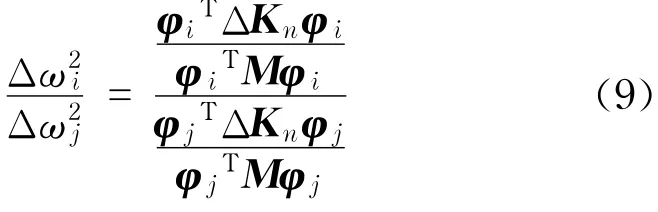
由式（9）可以看出，不同位置单元的损伤对应着特定的频率变化，也对应着不同的特定的频率变化比，根据结构损伤前后各阶模态的频率平方变化比，可以识别出结构损伤的位置，也可以对损伤的程度进行评估.

2 有限元模拟

本文运用ANSYS有限元软件模拟1根长0.9 m的悬臂工字型钢梁，截面基本参数如图1所示.所用材料的杨氏弹性模量为206 GPa，泊松比为0.3，密度为7 850 kg／m3.将工字型钢梁划分为30个单元，如图2所示.

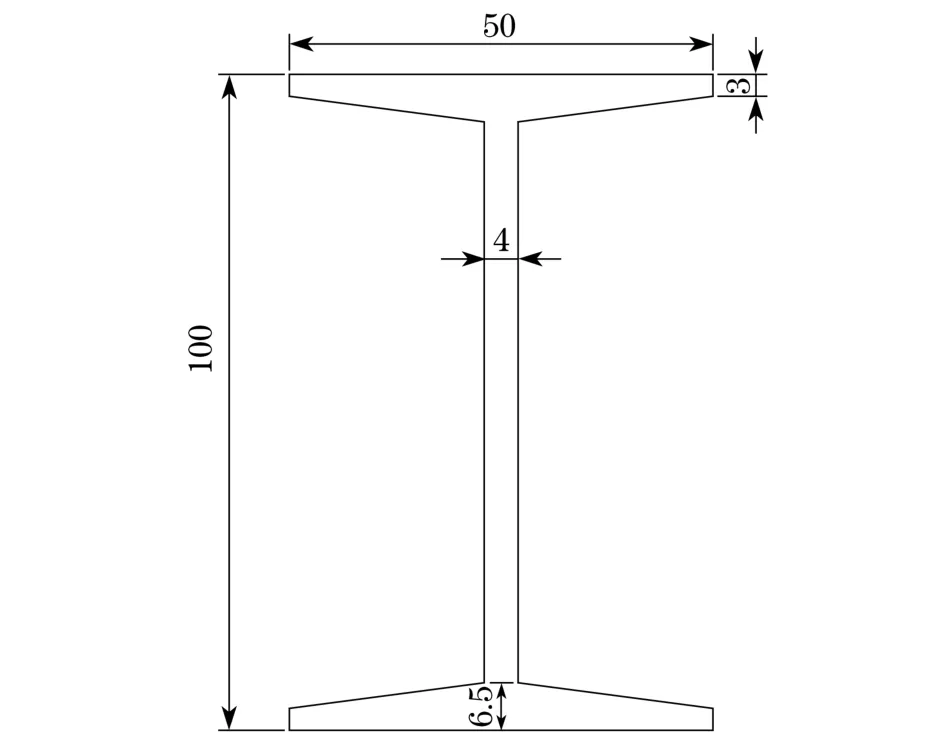
图1 工字梁横截面图Fig.1 Cross section view of H steel beam

图2 模型及单元划分示意图Fig.2 Diagram of beam model and element division

运用刚度折减来模拟工字型钢梁的损伤，计算结构振动前5阶频率，结构的11种工况分别为：

a.结构无损伤；

b.单点损伤程度递增，第15单元刚度分别折减5%，10%，20%，30%；

c.不同单点损伤，第3，8，22，29单元刚度折减20%；

d.多点损伤，第3，29单元刚度同时折减20%；

e.多点损伤，第3，29单元刚度同时折减30%.

模拟计算结果如表1所示.

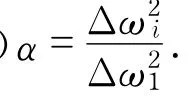
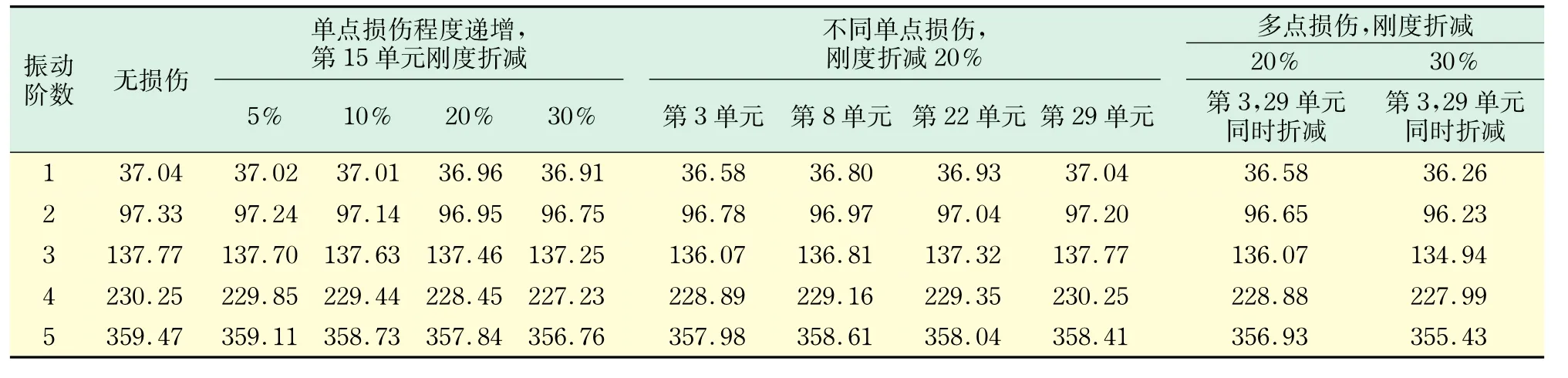
表1 有限元模拟各工况频率结果Tab.1 Frequencies under various working condition resulted by finite element simulation Hz_

由表1和图3可以看出，对于单点损伤，随着单元损伤程度的加深，各阶频率变化逐渐增大，在低频阶段，变化不大，在高频阶段，变化明显增大，而频率平方变化比随损伤程度的加深而减小；对于不同位置的损伤，由图3可以看出，损伤位置的不同对结构频率变化影响很大，损伤位置离固定端越远，频率变化越小，频率平方变化比越大，例如，第29单元损伤时，各阶频率基本无变化；对于多点损伤，其包含了单点损伤的变化信息，多点损伤时，频率减小更多；随着多点损伤程度的加深，频率平方变化比逐渐减小.

结构损伤识别通常是应用物理量或几何量发现结构中存在但较难通过常规的检测方法发现的内部损伤，所以，对第15单元损伤程度为5%的微损伤进行数值分析，其结果也是符合上述各阶频率变化的规律.

结构的振动信息可由单元的振动信息来反映，因此，可以通过频率平方变化比的方法来初步进行悬臂工字型钢梁的损伤定位，并对损伤程度进行初步评估，同时也说明了结构的有限元模拟的重要意义，为实现实际工程的检测奠定基础.

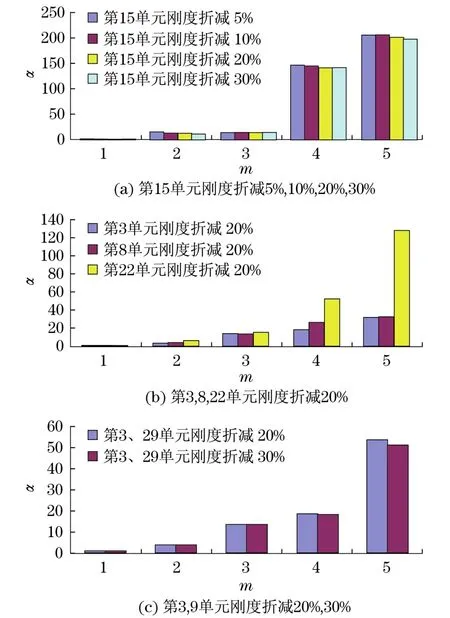
图3 结构频率平方变化比柱状图（有限元模拟结果）Fig.3 Histogram of square change ratio of structural frequency（finite element simulation results）

3 模型实验

以上述悬臂工字型钢梁为模型，进行了模态测试模型实验（材料为Q235钢）.将钢梁等间距划分为30个单元，从固定端开始编号.在钢梁的下表面第3，15和29单元中间位置粘贴传感器.

首先在梁结构无损伤状态下，采用单点激励得到结构的振动模态，激励和响应信号输入DASPV10专业版动态应变仪，利用MATLAB软件进行模态分析，实验得到前5阶模态，相干函数为0.85.

然后用砂轮机将钢梁单元切割成2 mm宽槽型切口，来模拟钢梁截面上出现损伤的状态，并进行振动测试实验.

实验共进行了10种工况的振动测试：

a.结构无损伤；

b.单点损伤程度递增，第15单元出现损伤，切口深度依次加深为2，4，6 mm；

c.不同单点损伤，第3单元出现损伤，切口深度为4 mm；第29单元出现损伤，切口深度为4 mm；

d.多点损伤，第3，29单元同时出现损伤，切口深度依次加深为4，4，6，6 mm，第15，29单元同时出现损伤，切口深度依次加深为4，4，6，6 mm.

实验所得频率数据如表2所示.

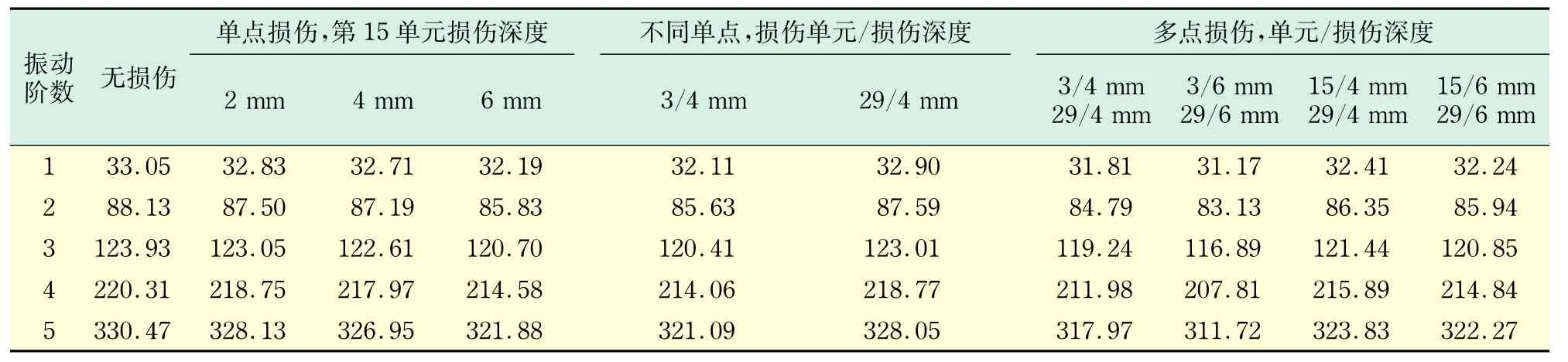
表2 模型实验各工况频率结果Tab.2 Frequencies under various working condition resulted by model tests_______________ Hz_

同时对测试的频率结果进行分析计算，以无损伤时的模态频率作为基础，计算频率平方变化比（前5阶变化与第1阶变化相比），得出m-α关系图，如图4所示.

从图4可以看出，在单点损伤和多点损伤状态下，结构频率表现出一定的变化规律.对于单点损伤，频率平方变化比随损伤程度的加深而减小；对于不同位置的损伤，损伤位置的不同对结构频率变化影响很大，损伤位置离固定端越远，频率变化越小，频率平方变化比越大；多点损伤也包含了单点损伤的规律.从实验数据分析结果来看，实验结果反映出与计算机模拟相同的规律.

4 结 论

a.根据基本振动理论推导了结构振动信息与损伤位置和损伤程度的函数关系式，运用频率平方变化比的方法可以初步进行损伤的定位和程度的评定.

b.实验数据分析结果所表现的规律与计算机软件模拟的结果具有一致性，验证了在研究结构的损伤之前，以有限元分析软件的计算结果作为理论指导的必要性.

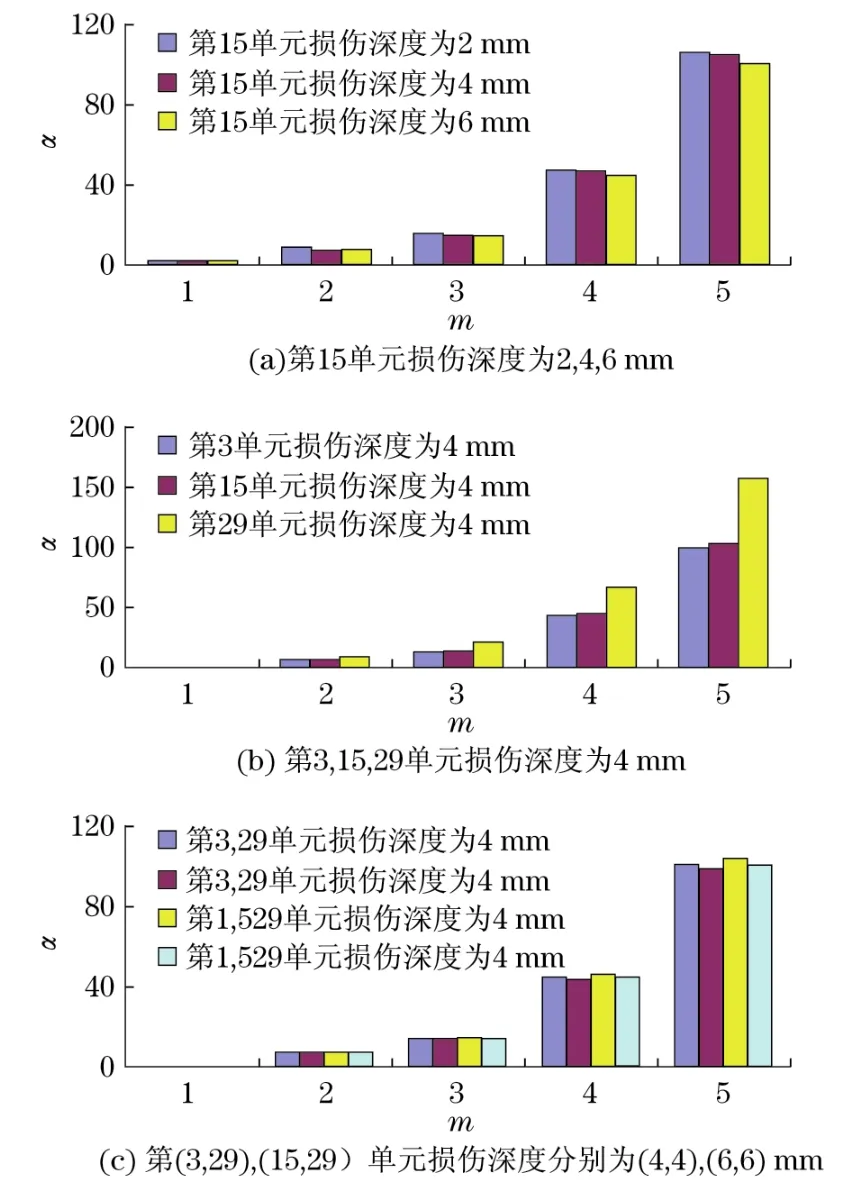
图4 结构频率平方变化比柱状图（模型试验结果）Fig.4 Histogram of square change ratio of structural frequency（model experiment result）

c.本文只讨论了频率平方变化比对在构件较少的结构损伤识别中的应用，此方法是否适用于多构件的结构损伤识别有待于进一步研究.

d.在实际工程中，测定结构振动模态时，往往有噪声的干扰，导致实测的结构振动的频率和振型与实际不符，影响评定效果.因此，研究出一种能够有效降低噪声干扰的损伤检测方法是亟待解决的问题.

［1］ Aktan A E，Brownjohn J M W.Structural identification：opportunities and challenges［J］.Journal of Structural Engineering，ASCE，2013，139（10）：1639-1647.

［2］ Salawu OS.Detection of structural damage through changes in frequencies：a review［J］.Engineering Structures，1997，19（9）：718-723.

［3］ Park G，Cudney H H，Inman D J.An integrated health monitoring technique using structural impedance sensors［J］.Journal of Intelligent Material Systems and Structures，2000，11（6）：448-455.

［4］ Schulz M J，Naser A S.Locating structural damage using frequency response functions［J］.Journal of Intelligent Material Systems and Structures，1998，9 （11）：899-905.

［5］ 郑明刚，刘天雄，陈兆能.基于频响函数的结构损伤检测［J］.机械科学与技术，2001，20（3）：479-480.

［6］ 汪之松，郭惠勇，李正良.基于频率响应的不同结构损伤识别方法研究［J］.工程力学，2008，25（6）：6-13.

［7］ 刘晖，瞿伟廉，袁润章.基于模态应变能耗散率理论的结构损伤识别方法［J］.振动与冲击，2004，23（2）：118-121.

（编辑：石 瑛）

Structural Damage Analysis of Cantilever H Steel Beam Based on Frequency Response

ZHOUKui， NINGNa-na， LIN Jie
（School of Environment and Architecture，University of Shanghai for Science and Technology，Shanghai 200093，China）

The vibration properties of cantilever Hsteel beam were investigated based on the basic theory of structural dynamics.Structural damage factor was derived as a function of damage location and damage degree.According to the structural frequency response，the frequency square change ratio method was used in preliminary testing and evaluation of structural damage.Finite element analysis software ANSYS was applied to simulate and analyse a cantilever Hsteel beam under 11 working conditions.In the similation，the element stiffness reduction was adopted to simulate structural damage.Then model tests for the H steel beam were carried out.The calculation and analysis results are of great significance to the damage detection and recognition of cantilever H steel beam structures.

structural damage；frequency response；cantilever H steel beam；finite element analysis；damage detection

TU 391文献标示码：A

1007-6735（2014）05-0497-05

10.13255／j.cnki.jusst.2014.05.017

2013-12-16

国家自然科学基金资助项目（51208300）

周 奎（1970-），男，副教授.研究方向：结构损伤检测.E-mail：zhoukui＿sh＠163.com