最小Q-特征值为给定整数的一类图
沈富强, 吴宝丰
(上海理工大学理学院,上海 200093)
最小Q-特征值为给定整数的一类图
沈富强, 吴宝丰
(上海理工大学理学院,上海 200093)
研究了基于二部图H构造的一类图的最小无符号拉普拉斯特征值,即最小Q-特征值,得到了它的最小Q-特征值的可达上界为1.给出了最小Q-特征值为1的2个必要条件,并构造了最小Q-特征值为1的一类图.另外,给出了利用H∨K1的最小Q-特征值来判断简单图H没有完美匹配的方法,以及图G增加边后最小Q-特征值保持不变的1个充分条件.最后,构造了最小Q-特征值为任意给定的正整数t的一类图.
无符号拉普拉斯矩阵;最小Q-特征值;界;完美匹配
1 基本概念
设G=(V,E)是简单图(不含环和重边),其中,V=V(G)={v1,v2,…,vn}为顶点集,n为顶点数,也称为G的阶数,E=E(G)为边集.A(G)= (aij)为G的邻接矩阵,当vi和vj相邻时,aij=1;不相邻时,aij=0.dG(vi)=|NG(vi)|为顶点vi的度,简记为di(i=1,2,…,n),D(G)=diag(d1,d2,…,dn)为度对角矩阵.在不致混淆的情况下,顶点集也记为{1,2,…,n}.
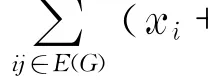
本文用qmin(G)表示图G的最小Q-特征值,相应的特征向量称为最小特征向量.qmin(G)≤δ(G),且当G(阶数n>1)连通时,qmin(G)<δ(G)[2],其中,δ(G)为G的最小度.众所周知,图G是二部图当且仅当qmin(G)=0[3],可以利用最小Q-特征值来判别图的二部性.

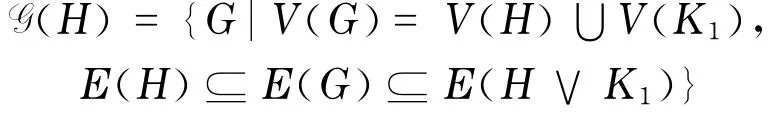
2 G(H)的最小Q-特征值
引理1[4]设A,B均为n阶实对称矩阵,则对于任意i=1,2,…,n,有

推论1 设A,B均为n阶实对称矩阵,则λn(A+B)≤λn-1(A)+λ2(B).

定理1 设H为二部图,则任意G∈G(H),有qmin(G)≤1.
证明 设H外的那一点与H之间有k条边相连.当k=0时,qmin(G)=0<1.当k=1时,qmin(G)≤δ(G)≤1,结论也成立.现证明k≥2的情形,设|V(G)|=n,则
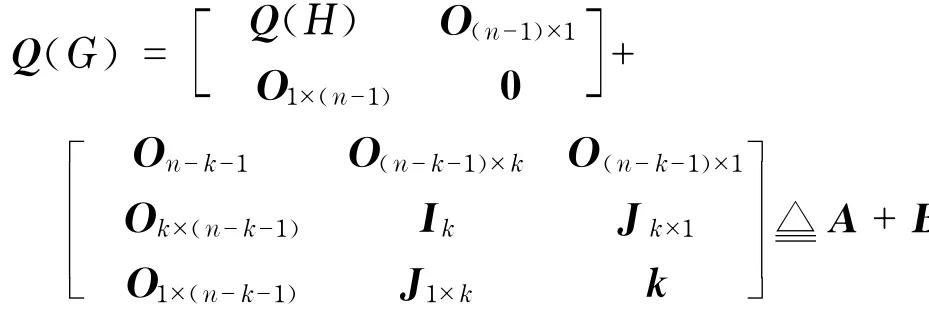
式中,J为全1矩阵;I为单位矩阵,则Spec(B)= (k+1,1k-1,0n-k),λn-1(A)=qmin(H)=0,λ2(B)=1.由推论1可知,qmin(G)≤qmin(H)+ 1=1.
引理4 设V1是图G的一个独立集,V1中任一点的邻点集均为V2,则G的Q-谱中至少包含|V1|-1个特征值|V2|.
证明 记V3=V(G)\(V1∪V2),设x是|V(G)|维向量,其中,V2∪V3对应分量0,V1对应分量x1,x2,…,x|V1|,满足x1+x2+…+ x|V1|=0,则
对于V1中的点i,
引理5 设G为完全三部图K1,r,s,若r≠s,则qmin(G)<1.
证明 K1,r,s=Kr,s∨K1∈G(Kr,s),根据定理1,qmin(G)≤1,现只需证1不是Q(G)的特征值.设V1,V2是Kr,s的二部,其中,|V1|=r,|V2|=s,r+s=n-1,由引理4可知,G的Q-谱中包含r-1个特征值s+1,以及s-1个特征值r+1.其余3个特征值可以通过后面定义的矩阵B来求得. 设x是Q(G)的特征向量,V1对应分量x1,V2对应分量x2,余下那一点对应分量x0,则有
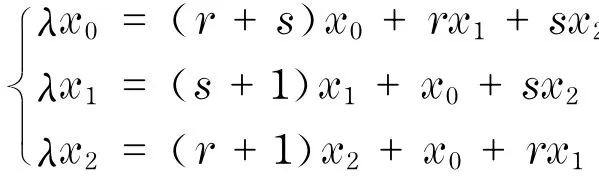
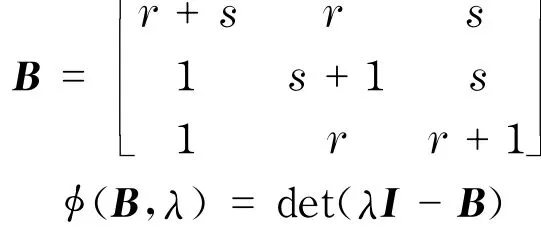
则φ(B,1)=det(I-B)=(r-s)2,从而当r≠s时,1不是Q(G)的特征值,所以,qmin(H)<1.
文献[6]提出了一个问题:是否存在Kp 1,p 2,…,ps (s≥3)是Q-整图,引理5表明,当s=3时,若p1=1,p2≠p3时,它的最小Q-特征值小于1大于0,故此时Kp 1,p2,p3不可能为Q-整图.
定理2 设二部图H的两部的顶点数分别为r 和s,若r≠s,则任意G∈G(H),有qmin(G)<1.
证明 显然G为K1,r,s的生成子图,由引理3(删边插值)和引理5得,qmin(G)<1.
引理6 设G为K1,r,s中删除K1与Kr,s之间的1条边后所得到的图,则qmin(G)<1.
证明 G∈G(Kr,s),由定理1可知,qmin(G)≤1,现只需要证qmin(G)≠1即可.设V1,V2是Kr,s的二部,若qmin(G)=1,由定理2可知,两部的顶点数相等,不妨均记为s,由引理4可知,G的Q-谱中包含2s-3个特征值s+1,其余4个特征值可通过后面定义的矩阵B来求得.设v∈V1是唯一不与K1相邻的点,x是Q(G)的特征向量,K1对应分量x0,V1\{v}对应分量x1,V2对应分量x2,v对应分量x3,则有
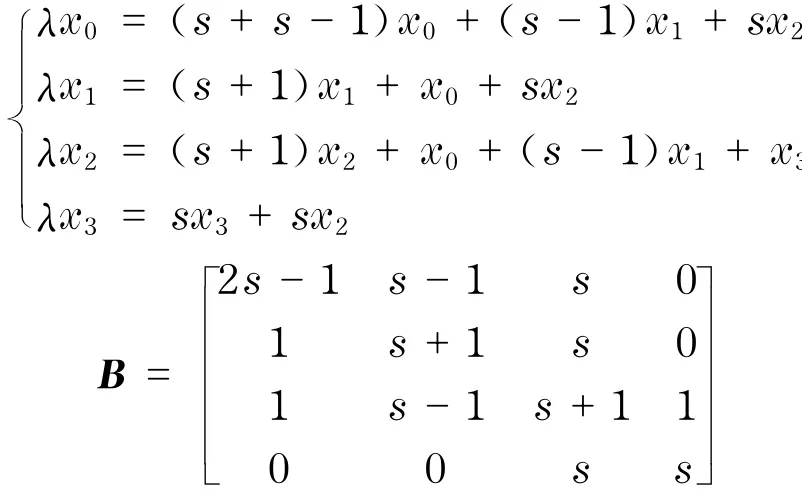
则φ(B,1)=det(I-B)=-2s(s-1).当s≥2时,1不是B的特征值.当s=1时,1为B的特征值,但此时G=P3,最小特征值为0,所以,qmin(G)<1.
定理3 设H为二部图,G∈G(H),若G≠H∨K1,则qmin(G)<1.
证明 根据引理3(删边插值)和引理6.
结合定理1~3,得到图类G(H)中最小Q-特征值为1的图的2个必要条件,即定理4.
定理4 设二部图H的两部的顶点数分别为r 和s,G∈G(H),若qmin(G)=1,则
a.r=s;
b.G=H∨K1.
3 最小Q-特征值为1的一类图
引理7[7]设G1为n1阶r1-正则图,G2为n2阶r2-正则图,则

引理8 设G=sK2∨K1,s≥1,则qmin(G)= 1,且x=(1,…,1,-1,…,-1,0)T是G的1个最小特征向量,其中,sK2的二部分别对应分量1,-1,K1对应分量0.
证明 sK2是1-正则二部图,根据定理5,qmin(G)=1.另一方面,
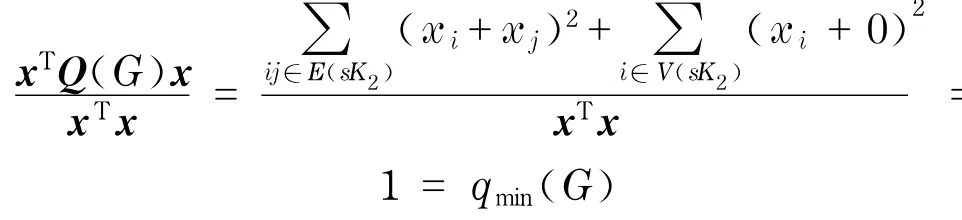
由引理2可知,x=(1,…,1,-1,…,-1,0)T是Q(G)的相应于1的特征向量,即最小特征向量.
定理6 设H为简单图,若qmin(H∨K1)<1,则H不存在完美匹配.
证明 假设H存在完美匹配,设H的顶点数为2s,则H包含1-正则生成子图sK2,由引理3(删边插值)及引理8得,qmin(H∨K1)≥qmin(sK2∨K1)=1,矛盾.
定理7 设G是图H增加1条边e=uv后所得到的图,x是Q(H)的最小特征向量,若xu+xv=0,则qmin(H)=qmin(G),且x也是Q(G)的最小特征向量.

根据引理8和定理7,若G=sK2∨K1,在sK2的二部之间随意添加边,G的最小特征值保持不变.于是,得到一类图,它的最小特征值均为1.记π={H∨K1|H是在sK2的二部之间添加若干条边后所得到的图,s为任意正整数},则任意G∈π,有qmin(G)=1,此时,H总包含1-正则生成子图sK2,故H存在完美匹配.于是,有定理8.
定理8 设H为二部图,存在完美匹配,G= H∨K1,则qmin(G)=1,且x=(1,…,1,-1,…,-1,0)T是G的最小特征向量,其中,H的二部分别对应分量1,-1,K1对应分量0.
在定理8中,H存在完美匹配并不是qmin(H∨K1)=1成立的必要条件,图1中的H∨K1的Q-谱为(8,42,22,12),显然,qmin(H∨K1)=1,但H没有完美匹配.
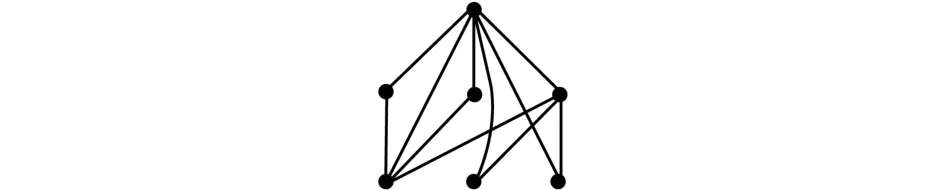
图1 H∨K1Fig.1 H∨K1
4 最小Q-特征值为t的一类图


引理9的证明类似引理8,再根据定理7,对图加边后最小Q-特征值不变的条件,得到定理10,定理10给出了最小Q-特征值为任意给定的正整数t的一类图.
[1] Cvetkovic'D,Doob M,Sachs H.Spectra of graphs:theory and applications[M].New York:Academic Press,1980.
[2] Das K C.On conjectures involving second largest signless Laplacian eigenvalue of graphs[J].Linear Algebra Appl,2010,432(11):3018-3029.
[3] Cvetkovic'D,Rowlinson P,Simic'S K.Signless Laplacians of finite graphs[J].Linear Algebra Appl,2007,423(1):155-171.
[4] Horn R A,Johnson C R.Matrix analysis[M].Cambridge:Cambridge University Press,1985.
[5] Cvetkovic'D,Rowlinson P,Simic'S K.Eigenvalue bounds for the signless Laplacian[J].Publ Inst Math,2007,81 (95):11-27.
[6] Zhao G P,Wang L,Li K.Q-integral complete r-partite graphs[J].Linear Algebra Appl,2013,438(13):1067 -1077.
[7] de Freitas M A A,de Abreu N M M,Del-Vecchio R R,et al.Infinite families of Q-integral graphs[J].Linear Algebra Appl,2010,432(9):2352-2360.
(编辑:石 瑛)
A Class of Graphs with a Given Integer as Least Q-eigenvalue
SHENFu-qiang, WUBao-feng
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)
When H is a bipartite graph,the least signless Laplacian eigenvalue(the least Q- eigenvalue)of a class of graphs constructed by H was studied.It was shown that the sharp upper bound of the least Q-eigenvalue of the class of graphs is 1.Moreover,two necessary conditions were given for the graphs whose least Q- eigenvalue is equal to 1,and a class of graphs was constructed which have eigenvalue 1 as their least Q- eigenvalue.Also,a method was presented for checking a graph H without a perfect matching by using the least Q eigenvalue of H∨K1,and a sufficient condition was given when adding edges without changing the least Q- eigenvalue.At last,a class of graphs were constructed which have least Q-eigenvalue t,where t is a given positive integer.
signless Laplacian matrix;least Q- eigenvalue;bound;perfect matching
O 157.5文献标示码:A
1007-6735(2014)05-0425-04
10.13255/j.cnki.jusst.2014.05.003
2013-08-16
国家自然科学基金资助项目(11301340,11201303,11101284);上海市自然科学基金资助项目(12ZR1420300)
沈富强(1988-),男,硕士研究生.研究方向:代数图论.E-mail:shenfuqiang19881230@126.com
吴宝丰(1978-),男,讲师.研究方向:代数图论.E-mail:baufern@usst.edu.cn

