消除冗余循环前缀的水声信道OFDM频域均衡算法

冯成旭，许江湖，罗亚松

(海军工程大学电子工程学院，湖北武汉430033)

OFDM作为一种频带利用率高的水声通信技术在海洋开发、海底勘探、水下作战领域得到了广泛应用[1]。为了克服水声信道多径效应所引起的码间干扰和误码率下降问题，基于训练序列的时域均衡技术[2]以及不需要训练序列的时域盲均衡技术得到了广泛发展[3]，为了更好利用OFDM通信信号的特征，适用于OFDM信号的频域均衡技术[4]受到了广泛关注，研究表明频域均衡技术具有收敛速度快、抗多径能力强等优势，但是传统频域均衡算法一般需要加入较长的循环前缀[5](CP)，这就占用了大量的通信带宽，对于带宽资源有限的水声通信系统来说影响较大。

为此，本文对依赖冗余循环前缀的传统OFDM频域均衡算法进行了改进，为频域均衡器引入了多级判决反馈机制可以在不需要CP参与情况下，有效克服水声信道中的多径效应，保证水声通信系统的可靠运行。

1 多径效应对OFDM信号的影响分析

OFDM是一种将宽带数据信息流分割成多个窄带独立数据信息流，且并行传输的技术[6]，其通信信号的调制与解调可以分别采用快速傅里叶反变换IFFT和快速傅里叶变换FFT来实现，为了得到时域通信信号，可从V点IFFT的V/2个正交子载波中选取N个进行使用，这N个子载波的频率按如下公式计算:

式中:fsam是信号时域采样速率，fi代表第i+1个子载波的频率，f0代表初始m0号子载波频率。结合发送的信源信息，对N个子载波上的频域值X(s)进行赋值，然后进行V点IFFT，即得到以fsam抽样的OFDM通信信号:

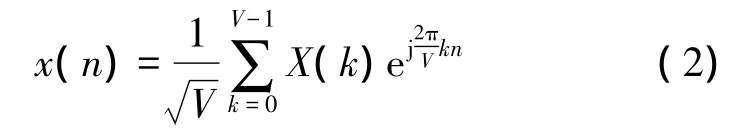
在理想情况下，接收端只要对接收信号进行FFT运算，即可恢复出信源X＇(k)，但是，水声信道中的多径效应会给OFDM通信系统造成大量误码。为了减少多径效应的影响，一般为OFDM通信系统加入循环前缀(CP)，以此作为码元间的保护间隔[6]，如图 1所示。

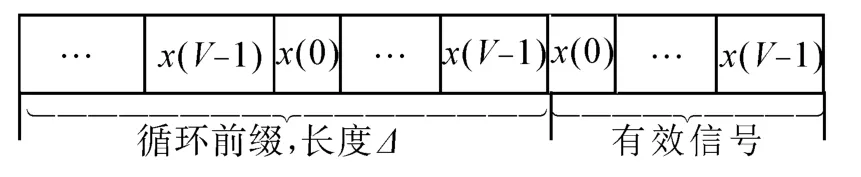
图1 OFDM信号的码元结构图Fig.1 Structure of the OFDM code element

设循环前缀长度为Δ，此时OFDM码元周期T'变为了T+Δ，第m个码元的时域信号如下所示:

式中:g(t)是宽度为T＇的矩形窗函数，Xm(k)是第m个码元中第k个子载波上的频域值。假设水声信道响应可表示为

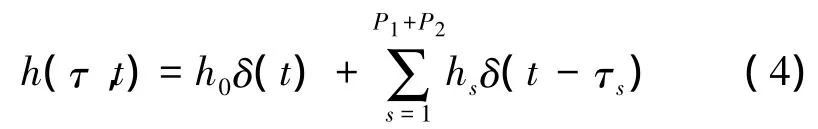
式中:hi、τi(i=1，2，…，P1+P2)分别是水声信道第i条多径的幅值和时延量，P1、P2分别是满足τi≤Δ、τi＞Δ的多径数。根据上述OFDM信号解调原理，可得到第m个码元的恢复信息Ym(k)如式(5)所示，Sa(t)=sin t/t是抽样函数。

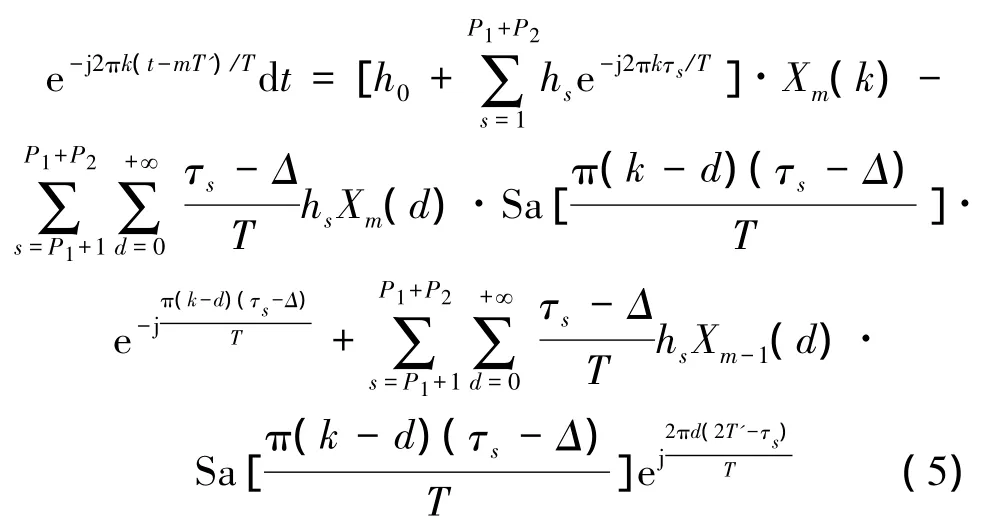
由式(5)可知，多径效应对OFDM信号的影响分3项:第1项为频率选择性衰落，第2项是子载波间的干扰，第3项是码间干扰ISI，这些干扰将使信源信号发生严重畸变，造成大量的通信误码。

2 传统OFDM频域均衡算法

由式(5)可见，当P2=0时，即循环前缀的长度大于最大信道多径时延值时，OFDM只受频率选择性衰落的畸变影响，这可利用传统均衡方法较好地进行补偿[7]。

假设OFDM第m个码元的发送信号为Xm=[Xm(0)，Xm(1)，…，Xm(V-1)]T，当 P2=0 时，接收到的恢复信息Ym=[Ym(0)，Ym(1)…Ym(V-1)]T可写成:

式中:H是水声信道h(n)的频谱，N为噪声频谱。在训练阶段，传统频域均衡算法使用长度为Ct个码元的已知训练序列xi(n)对均衡滤波器系数w(n)进行迭代调整，使得h(n)*w(n)接近于单径理想水声信道的冲激响应b(n)[8]。第i个码元的误差函数Ei为

式中:Wi、Bi分别是第i个码元时w(n)的频谱以及b(n)的频谱。根据LMS准则，Wi、Bi的迭代公式如(8)所示，其中uw、ub分别是调整步长。

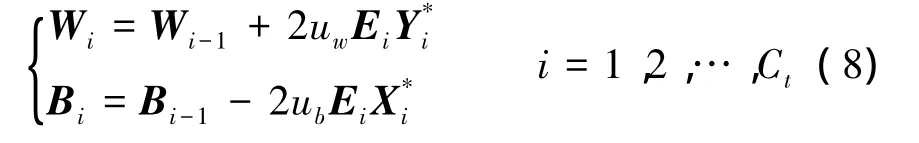
经过Ct个码元的迭代调整后，Wi和Bi可以较好地补偿多径效应造成的频率选择性衰落，此后对第i个(i＞Ct)码元的未知通信信号yi(n)进行FFT，并利用式(9)对yi(n)的频域值Yi进行多径补偿运算，即可完成通信信息的正确恢复。

后续仿真证明，当P2=0，传统频域均衡算法能够有效补偿频率选择性衰落，但是，当水声信道存在超过循环前缀长度的较长多径分量时(P2≠0)，由式(5)可知，这时恢复信号中还存在子载波间干扰和码间干扰，传统均衡算法的性能会大幅下降。

3 消除循环前缀的OFDM频域均衡算法

由上述可知，传统频域均衡算法通过添加较长的循环前缀来消除码间干扰和子载波间干扰[9]，但由于循环前缀不能有效传递信息，这会造成信道利用率的下降，限制OFDM优势的发挥。为此，本文希望提出一种新的频域均衡算法，能够主动对码间干扰和子载波间干扰进行补偿。传统频域均衡算法只利用了单个码元的信息，这不能较好体现码元间的相互关系，为此，在原有频域均衡器基础上，加入多级码元机制，同时由于反馈均衡器具有更强的跟踪和最小相位补偿能力[10]，在OFDM频域均衡器中引入反馈机制，如图2所示。

图2 OFDM频域判决反馈自适应均衡算法示意图Fig.2 Sketch map of the OFDM decision feedback frequency-domain equalization algorithm

第i个码元周期的恢复频域信号Yi送入前馈滤波器 Wfi=[Wfi(1)，Wfi(2)，…，Wfi(t_i)]中进行处理，输出 pfi，其中，t_i为阶数，Wfi(j)=[Wfi(j，0)，Wfi(j，1)，…，Wfi(j，V-1)]T是 V 点列向量;反 馈 滤 波 器 Wbi= [Wbi(1)，Wbi(2)，…，Wbi(t_b)]具有与Wfi类似的结构，其阶数为t_b，判决器的输出值Xi作为Wfi的输入，在训练阶段为已知序列，在通信解码阶段为判决序列。由图2可知，判决反馈频域均衡器的误差信号表示为

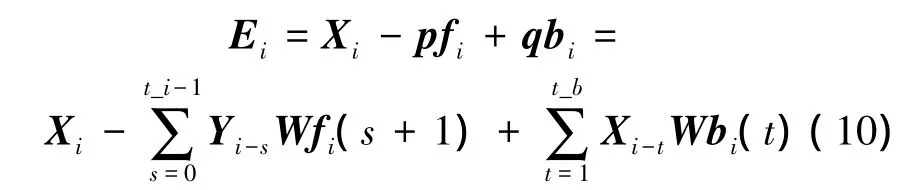
根据MMSE准则和计算量小的LMS算法，推导可得Wfi和Wbi的迭代公式如式(11)所示，其中s=0，1，…，(t_i-1)，t=1，2，…，t_b，μi(s)和 ρi(t)分别是i时刻的调整步长。为进一步收敛速度，迭代步长 μi(s)和 ρi(t)也利用 MMSE调整，如式(12)所示，Wf'i(s)、Wb'i(t)分别是式(11)中Wfi(s)、Wbi(t)关于μi(s)、ρi(t)的导数，具有式(13)的关系。

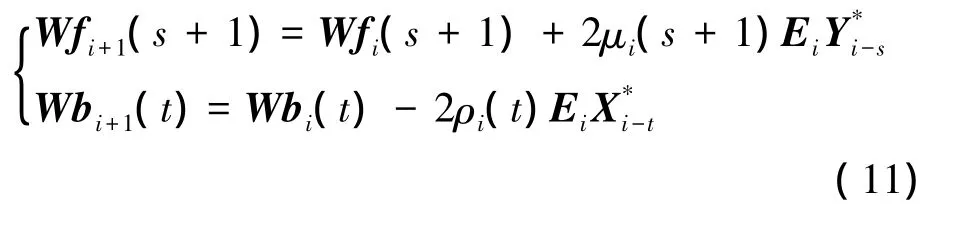
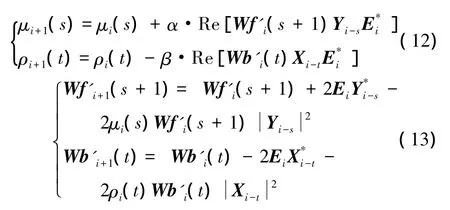
4 仿真结果及分析

假设OFDM信号的具体参数为:fsam=100，V=512 kHz，Tm=5.12 ms，N=48，采用二相键控(BPSK)进行子载波调制，带宽位于范围10.156～19.336 kHz内，在2个水声信道中进行仿真，具体信道参数如表1所示。

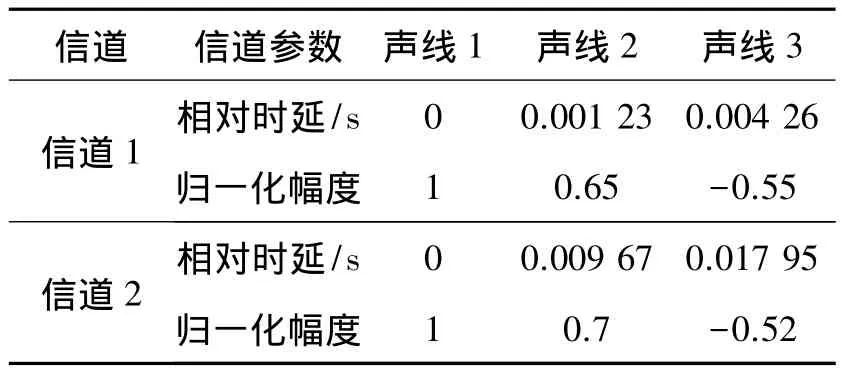
表1 信道的声线参数Table 1 Parameters of the acoustic channel rays

信道1的最大迟延为4.26 ms，为了避免码间干扰和子载波间干扰，将循环前缀长度 Δ设为5.12 ms，通信速率为 4 687.5 bit/s。图 3 为传统频域均衡算法在信道1下的效果图，仿真信噪比SNR=20 dB，可见，由于Δ大于水声信道最大径时延值，传统算法可以较好地对频率选择性衰落进行补偿。

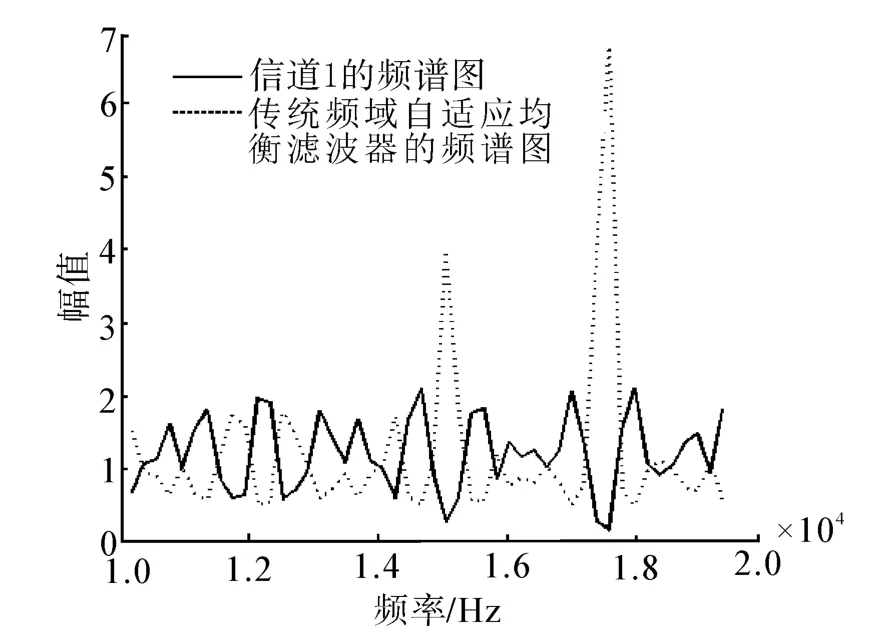
图3 传统频域均衡算法对信道1的补偿效果图Fig.3 Compensation effects of traditional frequencydomain equalization algorithm for channel 1

图4给出了相同仿真情况下，传统频域均衡算法对信道2频域选择性衰落的补偿效果图，可见，在深度衰落的频点位置，均衡算法的补偿能力较差，造成通信误码，这是由于循环前缀长度小于水声信道最大径长度造成的。

利用本文提出的判决反馈OFDM频域均衡算法，在不添加冗余循环前缀，即Δ=0条件下，对信道2的补偿收敛曲线如图5所示，算法调制步长初始值为0.01，均衡滤波器阶数t_i=4、t_b=2。根据处理流程，传统频域均衡器和判决反馈频域均衡器可分别用式(14)、(15)计算，其中k为子载波序号，由于只考虑有效通信带宽内的补偿效果，k的取值点个数为所使用子载波的个数N。

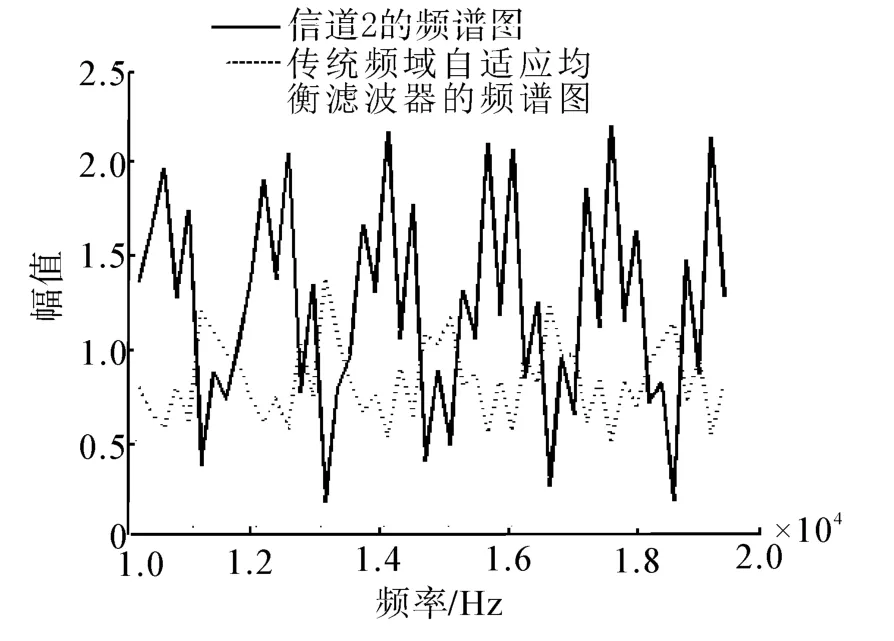
图4 传统频域均衡算法对信道2的补偿效果图Fig.4 Compensation effects of traditional frequencydomain equalization algorithm for channel 2

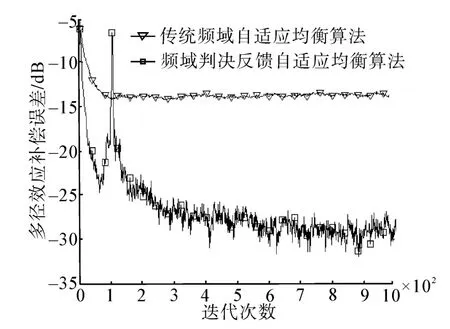
图5 信道2下，2种频域均衡算法的的补偿误差曲线Fig.5 Compensation error curves of the two frequency-domain equalization algorithms for channel 2

可见，即使没有冗余循环前缀，本文频域均衡算法仍能够对多径效应进行很好补偿，补偿误差较传统算法有近16 dB的提升，这时性能增益是由于多级缓冲机制以及判决反馈机制能够更好地反映码间关系引起的。2种算法的误码率性能曲线如图6所示。可见，由于传统算法不能对深度衰落有效补偿，误码率在10-1量级，而判决反馈均衡算法在较高信噪比时可以达到10-3量级，利用简单的纠错编码，即可实现无误码通信传输，同时由于不需要冗余循环前缀，整个通信过程都处于有效状态，通信速率也提高到9 375 bit/s，这就能充分发挥OFDM带宽利用率高的优势。

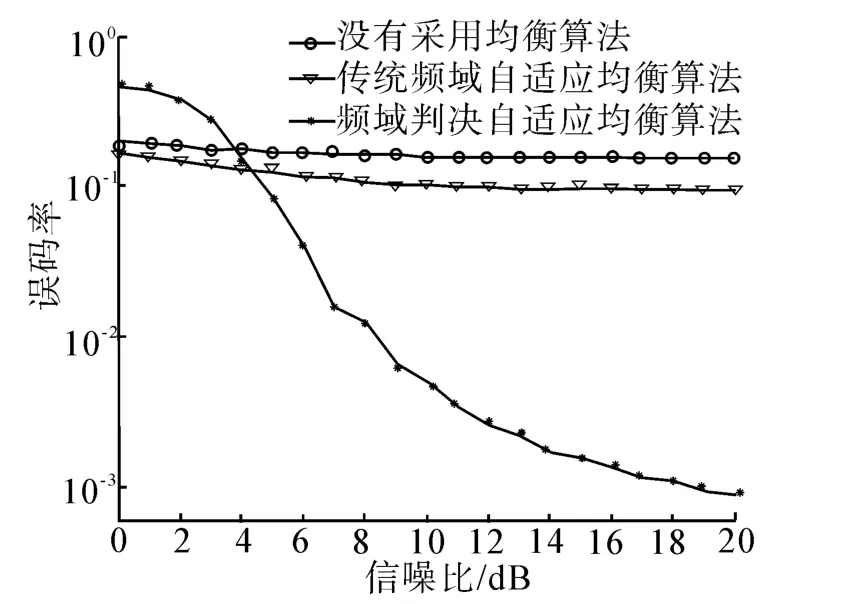
图6 信道2下，2种频域均衡算法的的误码率曲线Fig.6 Bit error rate of the two frequency-domain equalization algorithms for channel 2

频域判决反馈均衡算法在带来误码率、信道利用率性能优势的同时，多级、反馈机制会引起计算量的增大。实际上，由于OFDM通信信号只是利用了V/2可用子载波中的N个子载波，为了保证通信质量，可以对判决反馈频域均衡算法进行简化，简化算法只需对这N个子载波进行式(11)～(13)的均衡处理，而不需要对带外频域进行补偿，这相当于在频域上对N个子载波乘上一个矩形窗，对应于时域为接收信号与式(16)所示信号进行卷积，根据抽样函数Sa(t)的时域扩展性质，这会给接收信号带来额外的多径干扰，但多径时延仅为6V/N个抽样点数，影响较小，利用频域均衡算法很容易对其进行补偿。简化算法与未简化算法的误码率性能如图7所示，可见两者相差不大，但简化算法能将计算量变为原来的2N/V，大大降低了系统对硬件的要求，更利于在实际中进行应用。

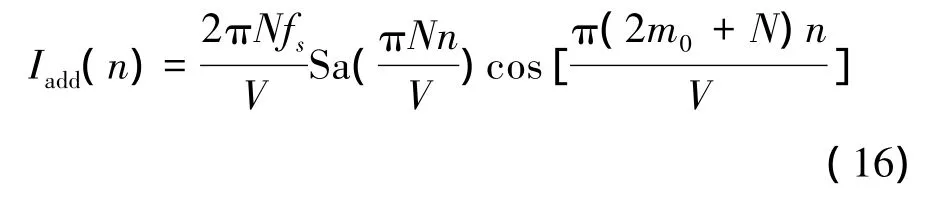
需要说明的是，本文提出的判决反馈频域均衡算法是利用多级和判决反馈机制来更加充分地反映OFDM码间存在的干扰，从而在不需要任何冗余循环前缀的前提下对多径效应造成的频率选择性衰落、码间干扰、子载波间干扰进行补偿，但是如果水声信道的长度过长，为了充分体现码间关系，前馈频域均衡器的阶数t_i不可避免也要增加，仿真发现，当前馈滤波器的时域长度不小于最大多径时延值dmax的1/4时，即t_i满足式(17)的关系时，通信效果较好。

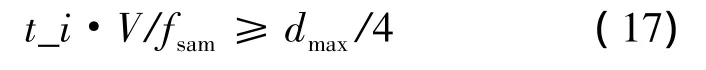
在实际使用时，根据水声信道的慢时变特性，可以定期利用成熟的MP、OMP等信道估计算法，对水声信道响应进行估计，根据估计出的结果，利用门限判决技术可以确定出水声信道的最大多径时延值dmax，根据dmax的大小，利用式(17)调整t_i，从而构成阶数自适应调整频域均衡算法，算法流程如图8所示。

图7 简化算法与未简化算法的误码率性能比较Fig.7 Bit error rate comparisons of the decision feedback algorithm and its simple algorithm

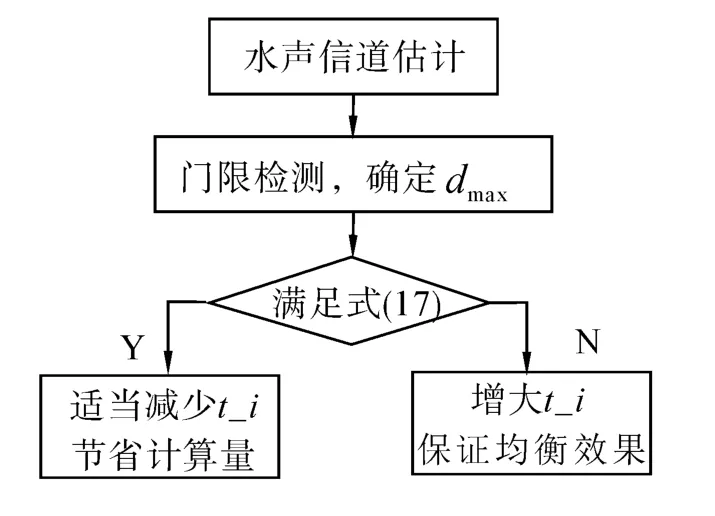
图8 阶数自适应频域均衡算法Fig.8 Order self-adaptive frequency-domain equalization algorithm

5 试验验证

为了对本文算法的有效性进行验证，在水池中进行了试验，采用BPSK信号进行通信，在没有均衡算法参与时，接收端得到的原始星座图如图9(a)所示，可见在多径效应影响下，通信相位图发生了畸变，造成误码率的大幅提高，而经过本文频域判决反馈自适应均衡算法处理后的星座图变得非常清晰，如图9(b)所示，保证了无误码数据传输，由此验证了本文算法的有效性，实验过程中算法的补偿误差曲线如图9(c)所示。

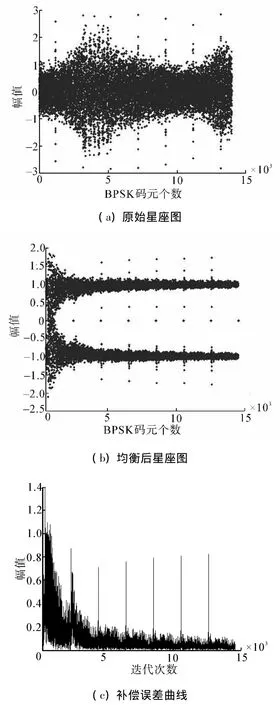
图9 水池实验效果图Fig.9 Results of the pool experiment

6 结束语

冗余循环前缀由于不能传输有效信息，会占用宝贵的水声信道带宽资源。为此，本文提出了一种新型的OFDM频域判决反馈均衡算法，通过仿真和实验，证明该算法可以在不添加冗余循环前缀的条件下，完成对水声信道多径效应的有效补偿，实现更高速、可靠的水下信息传输。在此基础上，针对新算法计算量增大的问题，本文提出了更利于工程实现的简化算法，并给出了实际应用中均衡器阶数的选择方案。

[1]DENIS B，PIERROT J B.Joint distributed synchronization and positioning in UWB Ad Hoc networks using TOA[J].IEEE Transactions on Microwave Theory and Techniques，2006，154(4):1896-1911.

[2]WU J，ZHENG Y R.Low complexity soft-input soft-output block decision feedback equalization[J]IEEE Sel Areas Communic，2008，26(2):281-289.

[3]BIANCHI P，LOUBATON P.On the blind equalization of continuous phase modulated signals using the constant modulus criterion[J].IEEE Transactions on Signal Processing，2007，55(3):1047-1061.

[4]罗亚松，刘忠，胡洪宁.用于多载波水声通信的频域判决反馈均衡算法研究[J].华中科技大学学报，2009，37(3):19-21.LUO Yasong，LIU Zhong，HU Hongning.Research on the frequency-domain equalization algorithm based on decision feedback structure designed for multi-carrier underwater acoustic communication[J].Journal of Huazhong University of Science and Technology，2009，37(3):19-21.

[5]BARHUMI I，LEUS G.Equalization for OFDM over doubly selective channels[J].IEEE Transactions on Signal Processing，2006，54(4):1445-1457.

[6]STOJANOVIC M.Adaptive channel estimation for underwater acoustic MIMO OFDM systems[C]//IEEE Digital Signal Processing and Signal Processing Education Workshop.Marco Island，USA，2009.

[7]郭业才，丁雪洁，郭福东.正交小波分数间隔频率分集自优化盲均衡算法[J].兵工学报，2010，31(3):285-290.GUO Yecai，DING Xuejie，GUO Fudong.A self-optimized blind equalization algorithm based on orthogonal wavelet transform and fractionally spaced frequency diversity[J].Acta Armamentarii，2010，31(3):285-290.

[8]JOSSO N F，ZHANG J J.Time-varying wideband underwater acoustic channel estimation for OFDM communications[C]//ICASSP.Dallas，USA，2010.

[9]KANG T，RONALD A.Iterative carrier frequency offset and channel estimation for underwater acoustic OFDM systems[J].IEEE Journal on Selected Areas in Communications，2008，26(9):1650-1661.

[10]AKYILDIZ F，DARIO P，TOMMASO M.Underwater acoustic sensor network:research challenges[J].Ad Hoc Networks，2005，3(3):257-279.