基于平均场均衡的Ad hoc网络路由协议

张旭，钱志鸿，刘影，王雪

(1.吉林大学通信工程学院，吉林长春130012;2.辽宁工程技术大学电子与信息工程学院，辽宁葫芦岛125105)

在当今资讯发达的社会中，无线网络已经变得越来越重要。近年来众多无线通信技术中，无线自组织网络以其快速组网、自主性和互联性获得了科研工作者的青睐。该技术的典型应用有战场通讯，灾难重建和搜寻营救操作，与此同时更多的商业应用也已经在开发中。在Ad hoc网络中，通信是通过多跳无线连接而并没有固定基础设施如基站等，因此它是自治的移动用户集合通过相对带宽受限的无线链路组网。由于节点是移动的，网络拓扑可能随时间快速改变且不可预测，物理层、媒质接入层和网络层是相互依赖相互作用的，因此在一个动态改变的网络中寻找一条链路去转发数据是很重要的。博弈方法在无线网络的应用中并不鲜见，主要集中应用于在用户间相互作用的模型建立以减少自私节点和协作节点。拓扑控制问题被研究建模为一种非合作博弈[1]。Huang[2-3]研究了具有无线通信背景的大规模LQG博弈。文献[4]介绍了一个基于纳什议价博弈的博弈理论框架以解决转发节点区域预留带宽的自私节点问题。文献[5]介绍了一种马氏跳变大种群随机多自主体系统的平均场博弈。文献[6]中提出一种域间路由协同监测激励策略。文献[7]介绍了一种基于博弈理论的无线传感器网络分布式节能路由算法。文献[8]提出了一种分布式二级路由协议(distributed two-tier routing，DTTR)。文献[9]介绍了基于非合作博弈的无线网络路由机制。考虑到无线网络的不稳定性、分布性等特点，同时将博弈论应用于无线网络研究时，博弈模型的收敛性也是需要考虑的一个关键问题，因此本文提出一种基于平均场均衡(mean field equilibrium，MFE)的方法，可以适当降低冗余信息产生的系统开销并提高网络效率。

1 平均场均衡模型

网络层的功能包括路由建立和更新以及沿途的数据包转发。一些问题如网络中的自私节点，不同路由技术对网络拓扑改变的收敛，以及不同路由节点行为等，都可以使用博弈论进行分析。

1.1 基本原理

在无线自组织网络中，节点间的连接是通过数据包或控制包的泛洪建立的。在这2种情况下，泛洪或转播是传送数据包至目的节点或在源节点和目的节点间寻找路径的最可靠技术。图1显示了无线自组织网络中源节点S需要转发数据给目的节点D，可目的节点在它的传输范围以外。所有位于源节点S无线传输范围内的都是它的邻居节点。通过简单泛洪搜寻路由，S将广播数据包并且这些数据将通过每一个S的邻居节点和那些接收到这些S的邻居节点数据包的节点转发，直到抵达目的节点。如果网络密度很大，将会存在很多冗余的信息广播包。

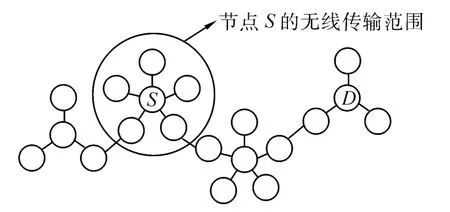
图1 无线自组织网络中节点转发策略Fig.1 Node forwarding strategy in Ad hoc network

这些冗余信息不仅仅使得路由选择复杂化，同时也会因共享信道的关系而降低网络整体性能。在一个共享媒质的环境里，大量的数据包开销增加了网络时延和碰撞的概率，因此最终导致较低的包投递率和吞吐量。博弈论的发明提供了冲突和竞争数学推理的基础。它已经成为一个丰富的理论，强大的数学和计算工具，同时更为直观。而使用该理论工具作为一个潜在的强大的路由分析工具另外2点原因:

1)路由协议可以被建模为一个网络和路由之间的博弈;

2)博弈的平衡点可以量化性能度量。

博弈论也广泛应用于经济学，社会科学，生物学和工程学科等[10-12]。采用一种博弈理论的包转发模型在节点数较多的网络中可以有效降低网络的泛洪。

1.2 系统模型

通过建立合理有效的模型对节点之间的相互行为进行分析，其中代理的数量假设为无限的，即“平均场”的模式。同时认为每个代理设置解决一个路由转发问题，但收益依赖于其他代理的行为。模型中描述为演变和代理行为。文中的随机博弈模型中，代理采取行动更新他们的状态，而且他们的收益和状态的转移可能受其余参与人的状态影响。考虑一个拥有m个节点的博弈。一个随机博弈是一个数组 Γ =(X，A，P，π，β)，定义如下:

1)时间:时间 t是离散的，t∈{0，1，…}。

2)状态:在t时刻局中人i的状态为 xi，t∈X，是紧致的。用符号x-i，t表示t时刻除了局中人i以外的其余人的状态。

3)行为:行为的数量为n，它们分别对应于一个代理可以选择在任何给定的时间的行动。假设节点行为的结果是二进制的，“转发”对应的节点获得一个单位的奖励，“不转发”对应的节点是零奖励。

4)类型:在任何给定时间的代理有一个类型，由一个随机变量a的值在[0，1]中给出。其中n个元素代表的是n个参数对收益分布的影响。代理的类型是不可观测的，这些参数之间的代理必须通过学习获取。在代理中a是独立同分布的。a群体测度记为 W，其中 W(A)表示概率，a∈A⊆[0，1]。

5)贴现因子β:贴现因子取值在(0，1)。

6)群体策略:xt为t时刻的一个普通代理状态随机变量，均匀地在人群中随机提取。然后在时间t的群体策略定义为以下的n维概率向量:ft=(E[σ (xt，1)]，E[σ (xt，2)]，…，E[σ (xt，n)])7)收益:单一阶段t时刻局中人i的收益为π(x，a，f)，本文认为回报是有条件独立的，一个代理接收单位收益转发的概率Q(θ(i)，f(i))，类型是θ和群体策略是f。假设，对于每一个固定的θ和 i，Q(θ(i)，·)是连续的。

8)状态转移:根据是否对应于所选择的臂的收益变量是1或0，局中人的状态对应的相应变量增加1。更准确地说，让yi，ni为单位基本向量，对应的行为是转发或不转发。因此，如果当前状态为x，更新到x+yi状态，如果是转发的话，反之则为z+ni。现在可以定义使用策略σ的代理的转移内核K。假设一个通用的代理的当前类型是θ，状态是x，群体策略为 f，那么

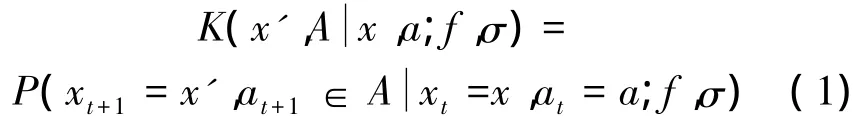
以上建立了平均场博弈模型，可以假设一个局中人的收益受其余人的经验分布影响，相同的假设应用于无线自组织网络中。收益依赖于其余局中人的行为，代理之间动态不同质，每一个时间步其余局中人的有限子集相互作用。上述模型中，局中人通过状态和收益函数相互作用，这种耦合是相互独立的。匿名俘获概念即是通过局中人状态信息的聚合来相互作用。一个代理的目的是最大化他的收益:

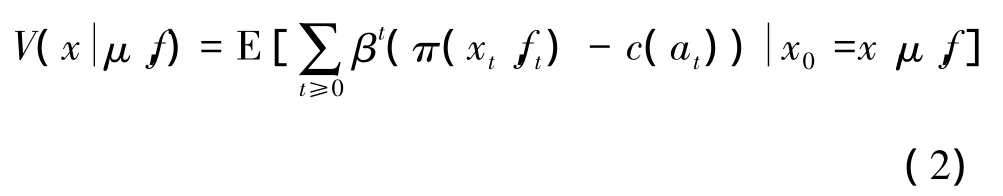
当局中人数目比较大时，假设一个局中人只响应其他局中人的长期平均状态分布f。则平均场预期的收益为

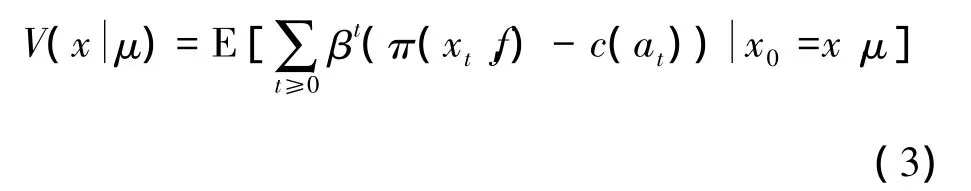
式中:μ是一个无视策略，仅依赖于xt。

1.3 收敛性分析

定义1 给定类型分布W，回报函数Q，策略σ，平均场均衡为(μ，f)，其中μ∈M是状态和类型的联合分布，f为群体策略，满足以下2个条件:

1)平稳性:对于任何状态x和任何类型的集A:

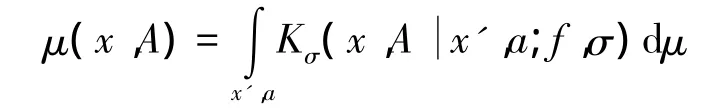
2)一致性:对所有的i

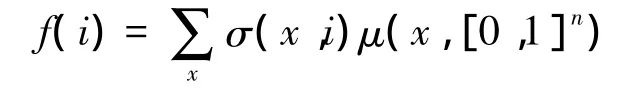
第1个条件要求μ在动态状态，群体策略为f时是稳态分布，代理策略为σ。第2个条件是f为μ完全稳态分布。2个条件一起确保该系统处于平衡状态。有以下的命题，建立存在的MFE。证明是通过拓扑不动点理论，根据假设，在群体策略中Q是连续的。

命题1 对于任何的策略σ，存在一个MFE(μ，f)。

证明:证明通过一系列引理进行，共分3个步骤:首先，给定的策略和固定的群体策略，产生的代理稳态分布是群体连续的。其次，这表明如果固定该策略和群体策略，并计算新的稳态分布引发的群体策略，初始群体策略的映射是连续的。该证明通过布劳威尔不动点理论完成[13-15]。

引理1 假设Pt(x|θ，f，σ)表示给定的代理状态的条件分布，其中θ，f和σ是固定的。那么Pt在f中是连续的。

引理2 对于任何策略σ和群体策略f，存在一个唯一的分布Φ(σ，f)满足条件1。此外，对于固定的σ，Φ(σ，f)在f中是连续的。

证明:当(σ，f)固定，转移核Pt(·|θ，f，σ)表示一个马尔科夫链状态空间。由于几何间隔更新的独立性，Φ(σ，f)可以显式的表示为更新间隔:

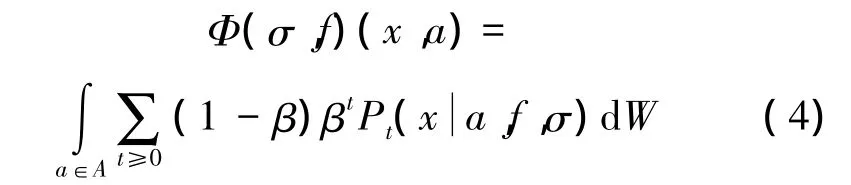
假设在欧几里德范数下 fk→f，根据引理1，Pt(x|a，fk，σ)→ Pt(x|a，f，σ)。根据有界收敛性，这表示对于所有的状态x和博雷尔几何A，Φ(σ，fk)(x，a)→ Φ(σ，f)(x，a)。因此 Φ(σ，fk)弱收敛于Φ(σ，f)。

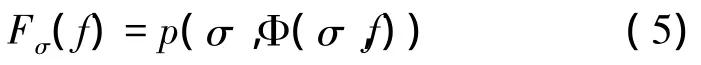
引理3 Fσ是连续的。

证明:在欧几里德范数下序列fk→f，根据引理2，有Φ(σ，fk)→ Φ(σ，f)。因为X是可分离的，根据Skorokhod定理意味着拥有随机变量(xk，ak)和相应的策略Φ(σ，fk)，以及一个随机变量(x，a)和相应的策略Φ(σ，f)使得(xk，ak)→ (x，a)。由于xk在一个离散空间，这表示存在一个ε，对于所有的k＞ε，xk=x。因此对于任何的 i，σ(xk，i)→ σ(x，i)。根据有界收敛定理可以得到:

由于Fσ是连续的并且映射自身一个紧致集，使用布劳威尔定理，存在一个不动点f*满足Fσ(f*)=f*。因此可以证明(σ，f*)可同时满足条件1和2。考虑M总的全变差距离度量dTV，使用以下dTV的等价参数。

定义2 总的全变差距离有以下的等价定义:

1)让 μ1，μ2∈M 是任意 2个测度，μ 是相对于μ1和 μ2绝对连续的任意测度。假设 ξ1，ξ2是 μ 的Radon-Nikodym导数，则:

2)F为所有博雷尔可测子集，则:

3)以 Ω(ξ1，ξ2)表示 2 个随机向量(x1，a1)和(x2，a2)的所有联合概率测度使得 k=1，2时，(xk，ak)的边缘分布为μk，则:

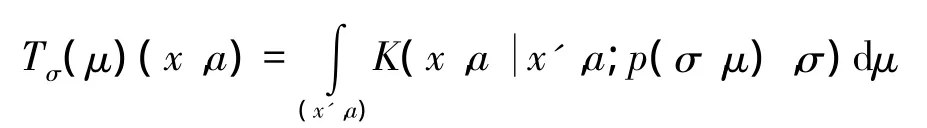
这里的K已经在式(1)定义过。注意到如果μ*是映射 Tσ 的不动点，那么 μ*和f*=p(σ，μ*)是一个MFE。相反地，在任何MFE(μ，f)中，μ必须是Tσ的不动点，f=p(σ，μ)被唯一地确定。因此给定一个策略σ，唯一的MFE存在当且仅当映射Tσ存在一个唯一的不动点。其充分条件为Tσ是一个关于总的全变差距离度量的收缩映射。这种条件也表示如果初始化系统为一个任意的初始分布μ∈M，在映射Tσ下考虑系统的演化，最终将收敛至一个MFE。

1.4 MFEA 算法

本文提出的平均场均衡的无线自组织网络AODV路由算法(mean field equilibrium AODV，MFEA)是基于按需平面距离矢量路由协议(Ad hoc on-demand distance vector routing，AODV)。在 AODV协议中，当源节点有数据要发送时，源节点需要广播一个路由请求包，当中包含了最新节点的序列号。邻居节点同样广播此分组，直到达到目的节点或者到达含有最新路由的中间节点为止。在节点转发请求包的过程中，记录经过的上游节点的ID，建立一条从源节点到目的节点的反向路由。AODV路由协议的带宽利用率高，并且是应用于变化的网络拓扑，但是由于在Ad hoc网络中节点移动频繁，对AODV路由协议路由表的维护较困难、可靠性低，而且部分节点的能量消耗过快，也会造成路由中断。

在AODV协议中，信息可周期性通过节点广播并用于链路监测，当节点M接收到来自节点N的信息，M意识到节点N在他的无线传输范围内并且是它的邻居节点。相反的，如果不能正确接收到信息则表明这是一个无效的链路。如果采用MFEA算法用于转发AODV路由协议，MFEA算法在源节点在发送广播分组的过程中，中间转发节点根据周围邻居节点的行为信息，通过计算出收益转发概率，进而决定是否作为中间转移节点进行数据分组转发，并且通过推算最大目的效益以及函数的迭代，更新中间节点的状态信息，最终到达目的节点，同时形成反向的路由路径。图2介绍了MFEA的系统流程。

算法描述:

1)当一个源节点S要寻找到目的节点D的路径时，首先要确定源节点S的当前时刻的状态，以及其余节点的状态信息，最开始网络上的节点是随机

给定任何策略σ，推导出MFE(μ，f)存在的充分条件，并且MFE收敛。考虑映射Tσ:分布的，根据前向分组格式{源地址，目的地址，序列号，跳数，行为，节点1，…节点N}初始化分组，执行2)。

2)当数据分组传送到下一个节点时，首先是判断为目的节点还是中间节点。如果是中间节点，根据周围节点的行为信息以及当前节点的类型θ，计算出节点的收益转移概率Q(θ(i)，f(i))，确定是否作为中间节点，同时根据转移概率，通过式(2)计算出最大目的收益，用值迭代函数计算均衡，使用新策略寻找下一个分布，最后计算误差及状态的累积分布，并将旧状态更新为新状态，重复执行2)。如果当前节点没有到下一跳的路由信息，则重新选择上游节点，重新执行2)。到达目的节点后，执行3)。

3)当分组到达目的节点后，根据后向分组格式{源地址，目的地址，序列号，跳数，行为，类型，转移概率，节点1，..节点 N}更新数据分组格式。当分组到达目的节点后，更新周围路由信息的同时，全局更新路径上所有的链路信息，执行4)。

4)沿着获得的反向路径信息发送数据分组，反向路径上的中间节点根据行为信息以及收益转移概率转移数据，重复执行4)直至到达源节点S。

5)源节点根据返回信息更新原路由信息。

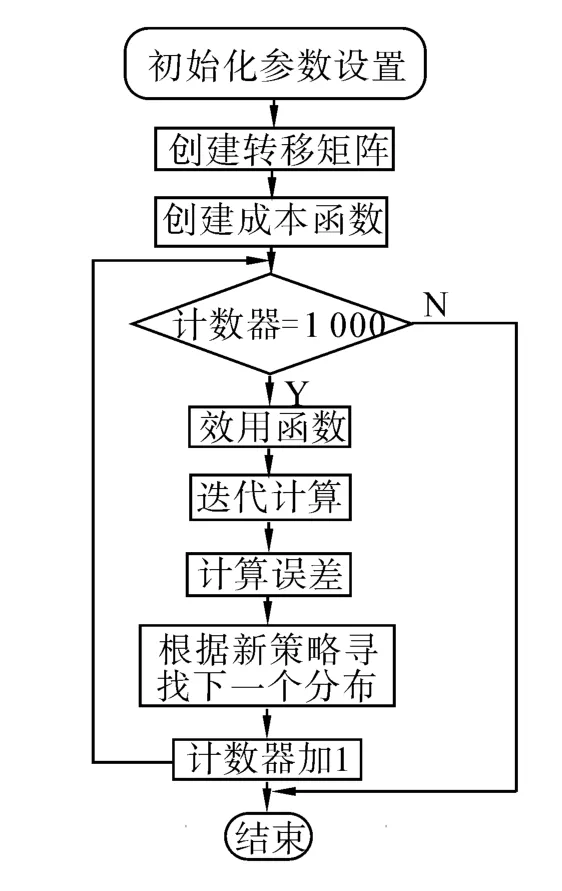
图2 MFEA流程图Fig.2 MFEA flow diagram

2 仿真结果与分析

前面介绍了博弈转发和纳什平均场均衡，根据给定的状态计算最优策略，下一个状态的计算主要根据公式递归求出。为了证明该方法对整体网络性能提升的影响，在网络模拟器NS-2中进行一系列试验。在模拟试验中，仿真参数见表1所示。

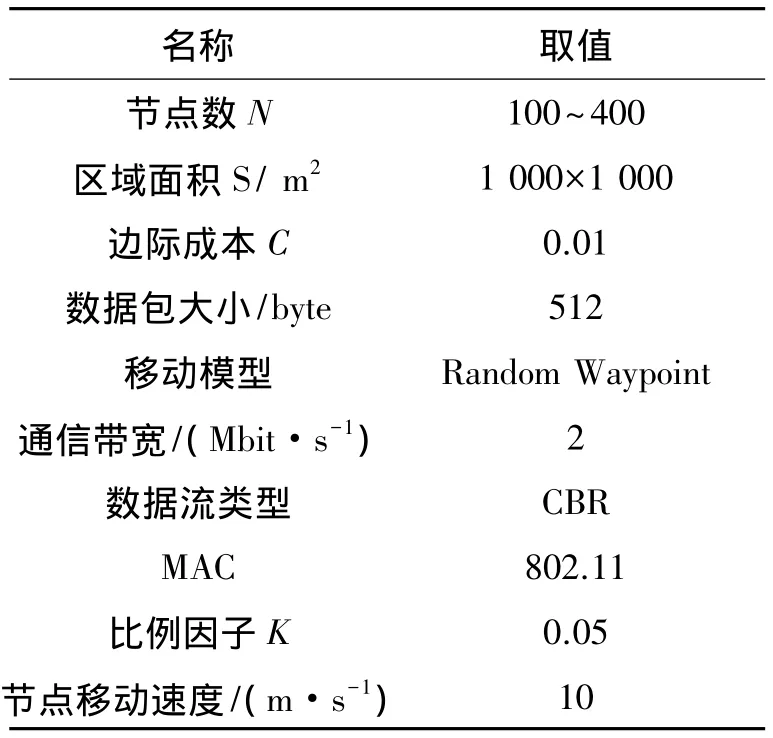
表1 仿真参数Table 1 Parameters for simulation

下面将分别对不同网络环境下的算法性能进行分析。无线自组织网络是一个动态的网络，首先仿真环境假设在不同的节点移动速度下进行，节点的移动速度设定为10 m/s，2种路由协议分别根据端到端的时延、分组投递率和系统归一化开销3种性能指标进行分析。

把网络建模为一个无向图G=(V，E)，这里V代表节点集合，E代表连接节点之间的链路集合。每个节点都有一个唯一的识别以便于路由协议可以识别他。

端到端时延:由于网络中链路可能被损坏以及节点随时的移动性，任意链路e=(m，n)∈E都会存在相对应的时延D(e)，链路的信道时延包括无线传播时延、队列时延及协议出路时间等。任意2个节点m和n之间的路径设定为P(m，n)=(m，e(m，x)，x，e(x，y)，y，… e(z，n)，n)。可以理解为任意2个节点之间的路径就是组成他们之间链路的所有可能节点的集合。一般来说，P(i，j)=P{P0，P1，…，Pn}，此时的Pi代表节点m和n之间的路径选择。延时定义如下:

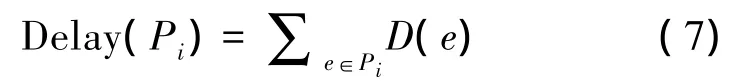
分组数据包投递率:目的端接收到的数据包数目与网络中实际发送数据包数目的比值，这个比率测量了发现路径的效率。假设发送了100个数据包给目的节点，最后接收到了60个数据包，那么网络中的数据包投递率即为60%，该度量反映了发送数据的成功率。

归一化开销:每一个数据包成功被目的节点接收时候所需要的路由包数目。这个性能反映了网络的拥塞程度以及节点的效率，开销较大的协议拥塞的概率相对大一些，并且会延迟队列中数据包的发送。

2.1 端到端时延

在节点数目由100～400变化的仿真实验中，对协议的3种性能进行了分析。图3比较了在不同节点数目情况下AODV路由协议和MFEA协议的平均端到端时延，可以看出MFEA方法中对于节点数目增加下的影响并不大，甚至在节点数目少的时候，AODV甚至延时低于MFEA协议可达0.05 s。不过当节点数目增加到150以上的时候，AODV的时延随着节点数目的增加显著增加。

这是因为在节点数目增加的情况下，网络中的变化复杂起来，路由的可靠性不能保障，因此AODV协议的时延增加较快;而MFEA由于采取了均衡的方法，在数据包转发的时候可以有效的进行转发，不受节点数目增多所引起的网络拓扑变化加快的影响，因此网络的延时并没有剧烈的变化，在节点数量为400时，MFEA算法的时延较AODV算法有将近0.2 s的提高，可见在大规模的网络中更加实用。

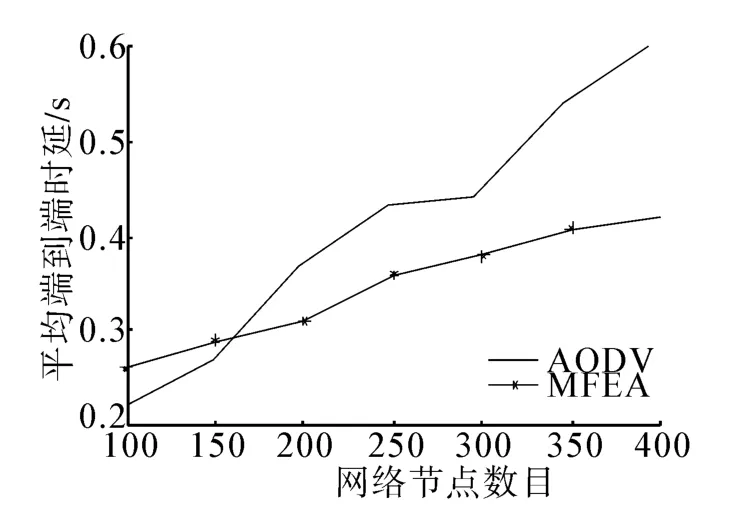
图3 MFEA流程图Fig.3 MFEA flow diagram

2.2 分组数据包投递率

图4为2种协议下的数据包投递率的性能比较。

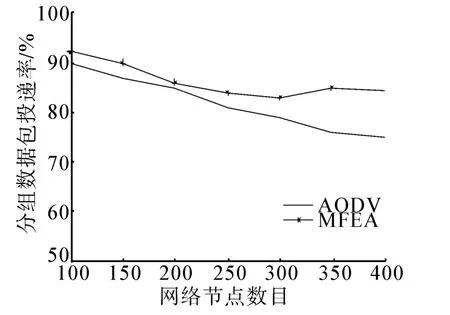
图4 不同节点数目下包投递率比较Fig.4 Packet delivery ratio vs.number of nodes

从图中可以看出，MFEA方法在节点数目较少的时候投递率性能与AODV相似，投递率在85%～90%左右。随着节点数目增加，MFEA协议性能明显优于正常的AODV协议，在节点数目较高的时候这种优势尤其显著，最高可达8%。这是因为网络规模较大的时候，AODV在拓扑变化频繁的网络下不能及时选择适当的路径以传播数据，同时在MAC层产生大量的数据碰撞也影响了整体的数据包投递率，而MFEA协议采用了均衡的方法，更能有效地适应于变化的网络拓扑。

2.3 归一化开销

从图5中可以看出当节点数目在100～400，MFEA方法的路由协议的归一化系统开销均低于AODV协议，最大可达10。这是因为AODV在这种情况下需要不停的寻找新的可用路径，从而产生大量的泛洪控制包，因此系统开销也会增加很多。而MFEA算法是一种仅需要长期状态平均的方法，它可以增加节点转发请求包概率，同时也可以减少因为网络拓扑变化带来的链路断开问题，降低了系统的开销性能。

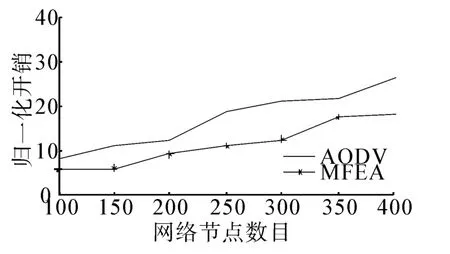
图5 不同节点数目下归一化开销比较Fig.5 Normalized overhead vs.number of nodes

3 结束语

本文介绍了一种基于平均场均衡的无线自组织网络路由协议，该方法对无线网络路由中的转发泛洪信息包求取平衡状态，最终达到减少冗余信息包，降低系统开销的目的。在节点数目100～400进行的仿真结果表明，本方法能有效地减少网络平均端到端时延，系统开销，同时也能增加包投递率，因此延长了网络的使用时间，从而提高了网络效率。

[1]EIDENBENZ S，KUMAR V S，ZUST S.Equilibria in topology control games for ad hoc networks[J].Mobile Networks and Applications，2006，11(2):143-159.

[2]HUANG M，MALHAM＇E P R，CAINES P E.Nash certainty equivalence in large population stochastic dynamic games:connections with the physics of interacting particle systems[C]//Proceedings 45th IEEE Conference on Decision and Control.San Diego，USA，2006:4921-4926.

[3]HUANG M，CAINES P E，MALHAM＇E R P.Large population costcoupled LQG problems with nonuniform agents:individual-mass behavior and decentralized ε-Nash equilibria[J].IEEE Trans Autom Control，2007，52(9):1560-1571.

[4]LU Bin，POOCH U W.A game theoretic framework for bandwidth reservation in mobile ad hoc networks[C]//Proceedings of the First International Conference on Quality of Service in Heterogeneous Wired/Wireless Networks(QSHINE’04).Dallas，USA，2004:234-241.

[5]王炳昌，张纪峰.马氏跳变大种群随机多自主体系统的平均场博弈[C]//Proceedings of the 29th Chinese Control Conference.Beijing，China，2010.WANG Bingchang，ZHANG Jifeng.Mean field games for large population stochastic multi-agent systems with Markov jumps[C]//Proceedings of the 29th Chinese Control Conference.Beijing，China，2010.

[6]郭毅，王振兴，程东年.基于博弈的域间路由协同监测激励策略[J].中国科学:信息科学，2012，42(7):803-814.GUO Yi，WANG Zhenxing，CHENG Dongnian.A game-theory-based incentive strategy for inter-domain routing cooperative monitoring[J].Scientia Sinica Informationis，2012，42(7):803-814.

[7]杨宁，田辉，黄平，等.基于博弈理论的无线传感器网络分布式节能路由算法[J].电子与信息学报，2008，30(5):1230-1233.YANG Ning，TIAN Hui，HUANG Ping，et al.Distributed energy-economical routing algorithm based on game-theory for WSN[J].Journal of Electronics＆ Information Technology，2008，30(5):1230-1233.

[8]胡静，沈连丰.基于博弈论的无线传感器网络分簇路由协议[J].东南大学学报，2010，40(3):441-446.HU Jing，SHEN Lianfeng.Clustering routing protocol of wireless sensor networks based on game theory[J].Journal of Southeast University，2010，40(3):441-446.

[9]汪洋，林闯，李泉林，等.基于非合作博弈的无线网络路由机制研究[J].计算机学报，2009，32(1):54-68.WANG Yang，LIN Chuang，LI Quanlin，et al.Non-cooperative game based research on routing schemes for wireless networks[J].Chinese Journal of Computers，2009，32(1):54-68.

[10]AUMANN R J.Handbook of game theory with economic applications[M].Amsterdam:Elsevier，1994.

[11]OSBORNE M J，RUBINSTEIN A.A course in game theory[M].Cambridge:MIT press，1994.

[12]GIBBONS R.Game theory for applied economists[M].Princeton:Princeton University Press，1992.

[13]ADLAKHA S，JOHARI R.Mean field equilibrium in dynamic games with complementarities[C]//2010 49th IEEE Conference on Decision and Control(CDC).Atlanta，USA，2010:6633-6638.

[14]WEINTRAUB G Y，BENKARD C L，Van ROY B.Oblivious equilibrium:a mean field approximation for large-scale dynamic games[C]//Neural Information Processing Systems.Vancouver，Canada，2005.

[15]IYER K，JOHARI R，SUNDARARAJAN M.Mean field equilibria of dynamic auctions with learning[J].ACM SIGecom Exchanges，2011，10(3):10-14.