基于Matlab迫击炮外弹道仿真
伍建辉 董 亮
(西安电子工程研究所 西安 710100)
0 引言
迫击炮是对遮蔽目标实施曲线射击的一种火炮,具有构造简单、操作灵活、造价低廉、弹道弯曲、最小射程近、射速快、可实时伴随步兵作战等特点,对开阔地及掩体内目标、各种野战工事、高大障碍物(如山坡)背后目标,有着良好的毁伤破坏作用,作为步兵近距离火力支援的有效武器,仍被现代各国军队大量装备。
迫击炮的外弹道设计是根据一定的战技要求,合理确定武器口径、初速及弹丸净质量,并以此作为内弹道设计、武器和弹药设计的必要依据,是进行迫击炮设计的首要工作。迫弹的运动是由其质心运动和绕其质心得转动所组成的,在迫弹初步设计和参数仿真阶段,为了能够便捷地获得迫弹的飞行弹道及其主要的飞行特性,研究过程通常分两步进行[1],首先,暂不考虑弹丸绕质心得转动,而将弹丸当做一个质点来研究;然后,在此基础上再研究弹丸绕其质心的转动运动。在质心运动和围绕质心运动分别研究后,再进一步研究他们之间的影响,这种方法在一般情况下具有足够的精度,且便于工程设计应用,同时易于搞清飞行动力学中一些问题的物理意义。本文讨论迫弹的质心运动并对此进行弹道解算。
1 直角坐标系下迫击炮外弹道质心运动方程建立
为了能把射击弹丸的运动规律当做质量集中于质心的质点运动规律,根据运动规律建立的微分方程组进一步简化,外弹道学引入了以下著名的基本假设[2]:
a.弹丸为理想的轴对称体,且在全部的飞行时间内攻角为0;
b.气象条件为标准气象条件;
c.地表面为平面,重力加速度g竖直朝下,垂直于炮口水平面且大小为g=9.80m·s-2;
d.忽略地球自转引起的科氏加速度;
在基本假设的条件下,弹丸没有围绕质心的运动,弹丸的飞行轨迹是一条在射击平面运动的理想弹道。此时弹丸只受重力和空气阻力影响。图1表示了弹丸的质心运动。

图1 直角坐标系内弹丸质心运动
图1中ax为空气阻力加速度矢量,axx、axy为ax在x,y轴的投影,g为空气加速度矢量。根据 图中的数学关系以及外弹道理论,x轴的加速度分量为:
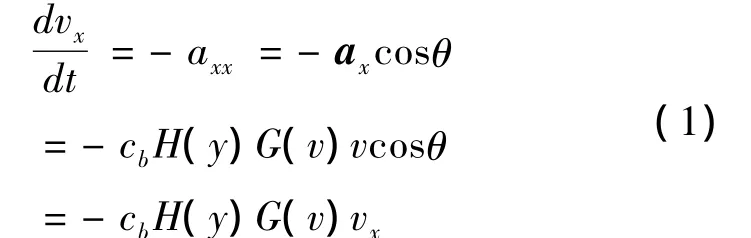
同理y轴的加速度分量为:
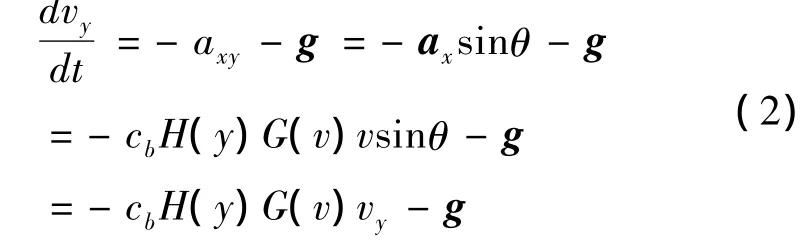
式中cb为弹道系数,H(y)为空气密度函数,G(v)为虚拟阻力函数。
根据上式以及运动学公式,可以建立以时间t为自变量的弹丸质心微分方程组如下[3]:

方程组中τ0N地面标准虚温;τ为虚温;θ为弹道倾角;
初始条件为

2 弹道仿真模型的建立
2.1 龙格-库塔算法及流程
弹道解算就是对上面的微分方程组的求解问题,一般对于微分方程y·=f(t,y)采用数值积分方法,用泰勒级数可求得tm+1时刻的精确解为[1]:

上式中ωi为待定的加权因子,r为使用k值的个数(即阶数);ki为不同点的导数f值,ci,aij为待定系数。
当r=4时,可得到著名的四阶龙格-库塔公式,具体公式为:

四阶龙格-库塔算法是数字仿真中广泛采用的数值积分方法,其截断误差为o(h5),计算精度较高,是可以自启动的单步法,需要存储的数据量少,但每步需要对f进行四次计算,计算量较大[4]。图2是龙格-库塔算法流程。
算法中四阶龙格-库塔算法在Matlab平台下可以自己编制子函数,也可用其自带函数ode45()实现。
2.2 积分步长h的确定
龙格-库塔算法的截断误差与步长的五次方成正比,如果减小步长h精度将会提高,但是步长减小,计算点数将会增加,积累误差将会相应增大,可能反而会降低精度,同时计算时间加长,计算速度降低,所以要处理好步长与精度之间的关系。根据实际应用,六自由度运动方程解算中步长小于0.005s,一般高射炮弹道解算取步长为0.5s,远射程地面火炮步长h=0.5~1s。

图2 外弹道解算的龙格-库塔流程
2.3 炮兵标准气象条件[3,5]
弹道解算涉及气象条件,我国炮兵使用的标准气象条件包括地面标准气象条件和空中标准气象条件两部分。
2.3.1 地面标准气象条件
气温t0N=15℃ 地面空气密度 ρ0N=1.206kg·m-3
气压 Pe0N=846.3Pa 地面虚温 τ0N=288.9K
相对湿度φ=50%
音速 cs0N=341.1m·s-1
无风无雨
2.3.2 空中标准气象条件(<30km)
空中气象条件包括以下气象诸元:
a.虚温
在对流层(y<9300m)
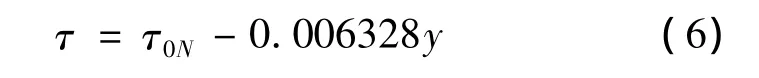
在亚同温层(9300m<y<12000m)和同温层(12000m <y<30000m)有不同的解析式,由于迫弹高程受限,所以本文不赘述。
b.空气密度函数H(y)
根据外弹道理论,对前苏联1943年阻力定律有经验公式:
y<9300m时,

此经验公式有足够的精度保证。
c.虚拟阻力函数G(v)
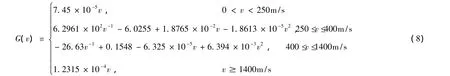
G(v)函数为分段函数,仿真中可以用逻辑函数的形式进行表述,可以使程序简洁可读性高。
另外在<30km高度内无风无雨。
3 弹道仿真结果分析
本文选择的炮弹种类为国产PP89式100mm迫击炮进行仿真,该炮的参数现已公开,口径100mm,初速308m/s,最大射程6.4km,射角范围:45°~80°,弹质量 8kg[6]。
仿真中将气象条件涉及的气象诸元函数代入,并取弹道系数Cb=0.8613,积分步长h=0.2s,仿真结果见图3-图6。
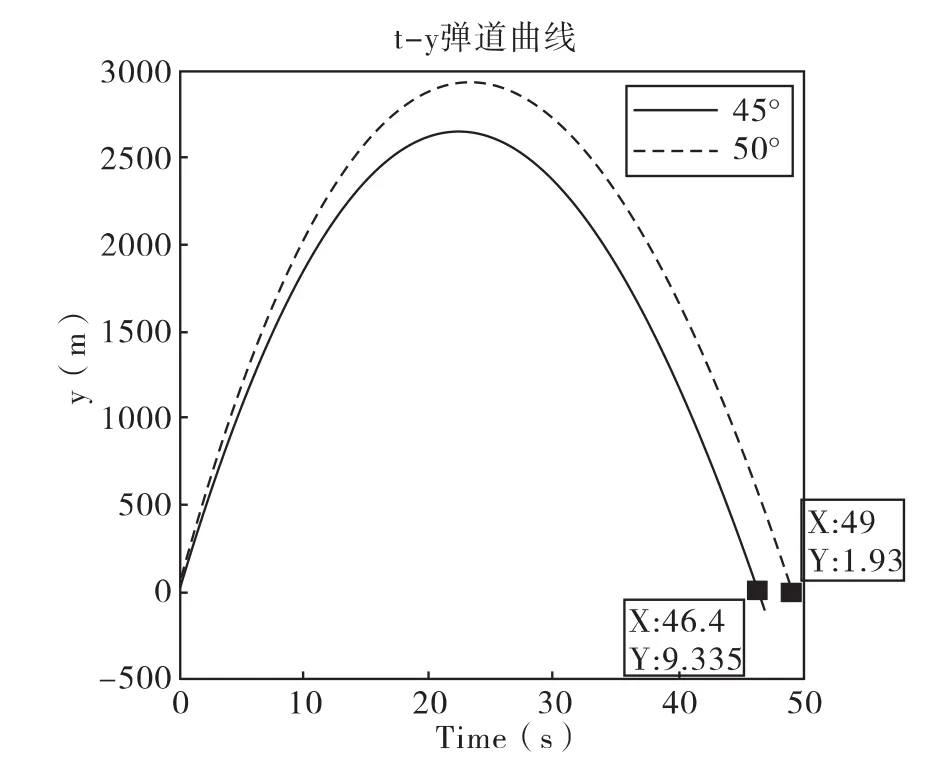
图3 射角 θ0=45°/50°时t-y弹道曲线

图4 射角θ0=45°/50°时x-y弹道曲线
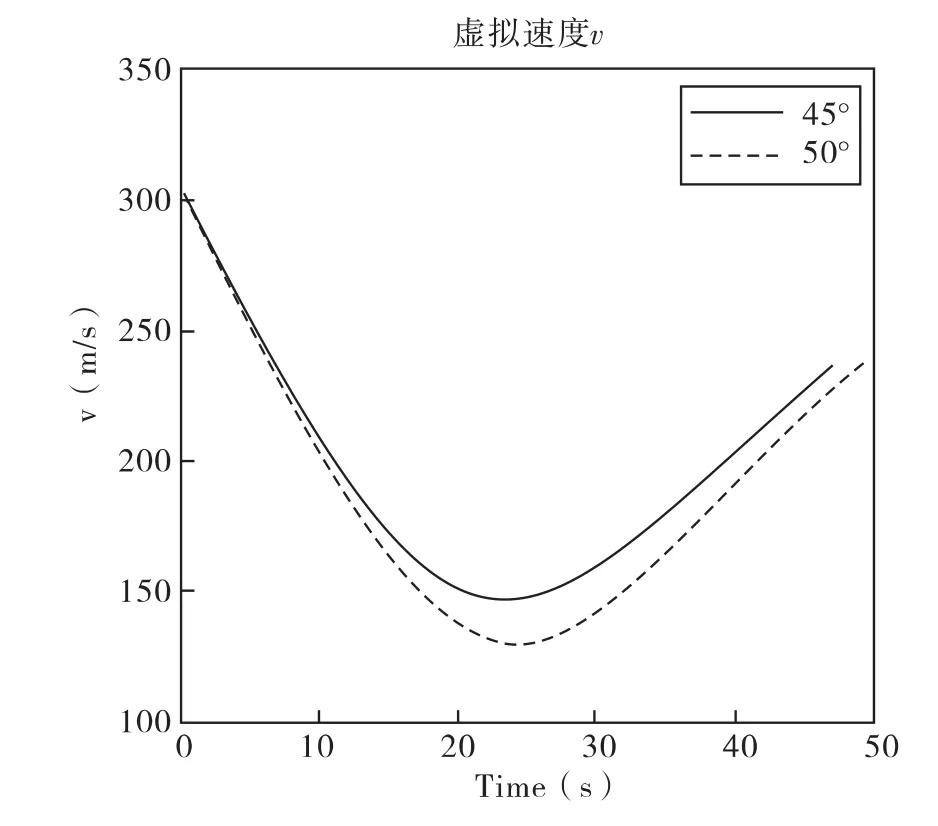
图5 射角θ0=55°/60°时速度v曲线
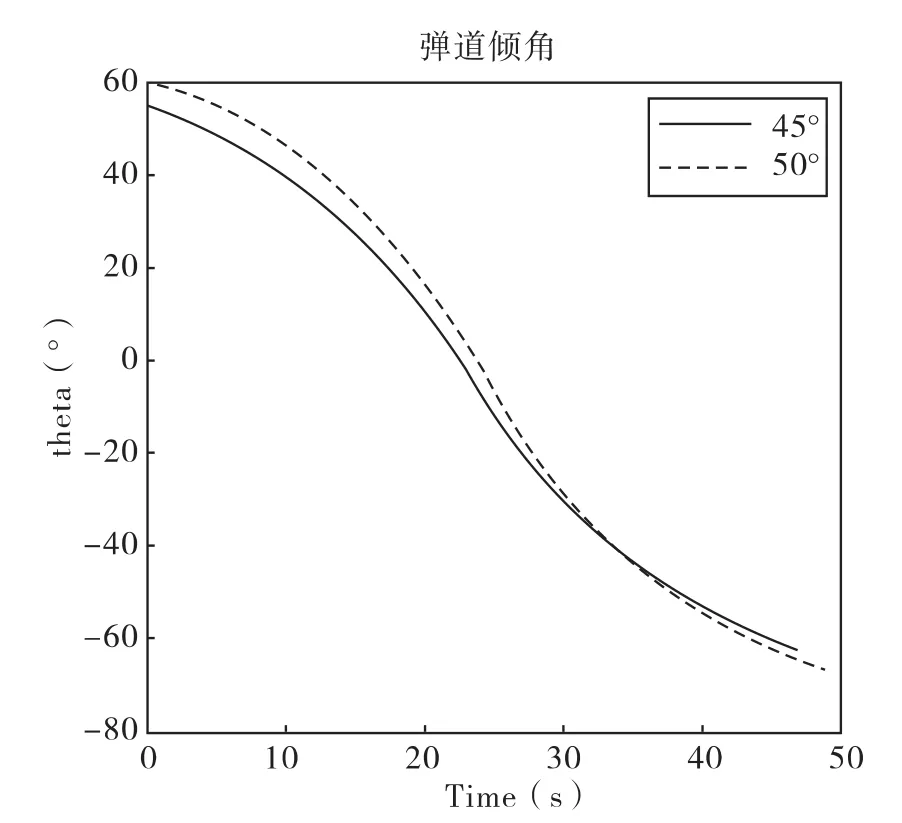
图6 射角θ0=45°/50°时弹道倾角曲线
PP89式 100mm迫弹在 45°下最大射程为6.4km,仿真结果为6448m。绝对误差为52m,相对误差为52/6400=0.812% ,说明该仿真模型能符合实际的实验效果,具有很高的可行性和可靠性。
从仿真结果来看,弹道特性完全符合空气弹道的一般特性,当初速、射角、弹道系数一定时,就可以确定一条弹道曲线。因此,只要改变模型中相应参数就可以得到任一初速、任一射角下的弹道诸元[7]。随着射角大小的改变,弹丸飞行时间、射程、弹道高程、落点速度都会做出相应的改变。
4 结束语
本文先建立迫弹运动质心模型,使用Matlab对迫弹弹道进行仿真,解算出弹道及部分参数的变化曲线仿真结果,该方法的优点在于建立模型比较简单,仿真精度比较高,同时程序可移植性高,曲线较完整地描述了弹丸运动的规律,对迫弹研制、安全飞行试验和落点散布研究等有着积极的意义。
[1]李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社.2005.
[2]马利兵,林都.基于Matlab的外弹道模型仿真研究[J].中北大学学报.2006,27(5):142-145.
[3]徐明友.火箭外弹道学[M].哈尔滨:哈尔滨工业大学出版社.2004.
[4] 李丹.四阶龙格-库塔法在火控解算中的应用[J].微计算机信息.2011,27(3):192-193.
[5] 韩子鹏等.弹箭外弹道学[M].北京:北京理工大学出版社.2008.
[6]国产 PP89式100mm炮击炮[J].轻兵器.2001,(12):45.
[7]段文龙,彭杰刚.基于Matlab/Simulink的弹丸外弹道6自由度运动仿真[J].重庆工学院学报.2009,23(4):146-149.

