多通道抽取FIR滤波器的FPGA高效实现
高 珊 李 鹏 单 聪
(1.西安电子工程研究所 西安 710100;2.装甲兵军事代表局驻西安地区军事代表室 西安 710000)
0 引言
多频连续波雷达是适应现代靶场高精度多目标参数测量需求的一种新体制雷达。该体制雷达,直波泄漏和近程地杂波的影响是不可忽略的[1~2],在双频模式时,不仅分布在零频,而且也分布在差频,对此可利用一定特性的滤波器予以滤除。另外,在现代靶场测量中,为了防止频谱混叠且为了满足实时信号处理的要求,需要对高采样的原始数据进行抗混叠滤波和降采样[3]。考虑到雷达的目标参数测量对回波的相位要求很严格,所以使用具有线性相位特点的数字FIR滤波器。
综合考虑在数字域对差频点的直杂波抑制处理以及抗混叠滤波和降采样,采用“高采样-低通滤波-抽取”的方法来实现。另外雷达的接收天线由四块微带平面天线阵组合而成,则实时信号处理系统接收的是多通道零中频复信号,所以整个实现是多通道抽取FIR滤波器的设计。
FPGA(Field Programmable Gate Array,现场可编程门阵列)技术的发展为DSP设计提供了一种新的选择,FPGA有着规整的内部逻辑块阵列和丰富的连线资源,特别适用于细颗粒度和高并行度结构特点的数字信号处理任务[4],如FIR滤波器、FFT等,相对于串行运算主导的通用DSP芯片来说并行性和可扩展性都更好。因此本文的多通道抽取FIR滤波器采用FPGA进行设计。当系统性能要求较高,则FIR滤波器的阶数很高,同时又要满足系统的实时性要求,对于多通道并行处理时,采用传统方法实现的FIR滤波器,FPGA资源耗费量将非常惊人;而采用串行处理时,系统的实时性要求又得不到满足,性能受到很大影响。基于此,本文从结构和方法两方面考虑,对多通道抽取FIR滤波器进行了优化设计,给出了不增加系统速度,又能显著减少资源的FPGA高效实现结构。
1 优化设计方法
1.1 FIR滤波器的结构优化
一个N阶的FIR滤波器差分方程:
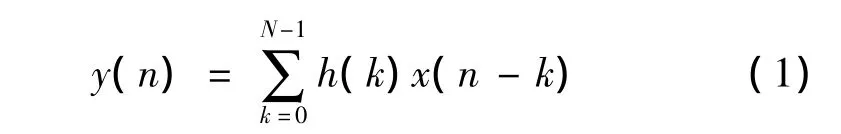
式中:x(k)为第k时刻的输入样本值;h(k)为第k级抽头系数;y(n)为滤波器的输出信号。
对于线性相位FIR滤波器,它的冲击响应h(n)具有中心对称性,即
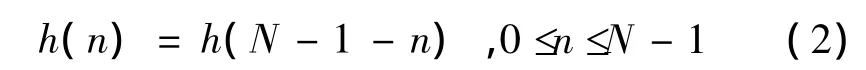
则式(1)将变为如下的形式
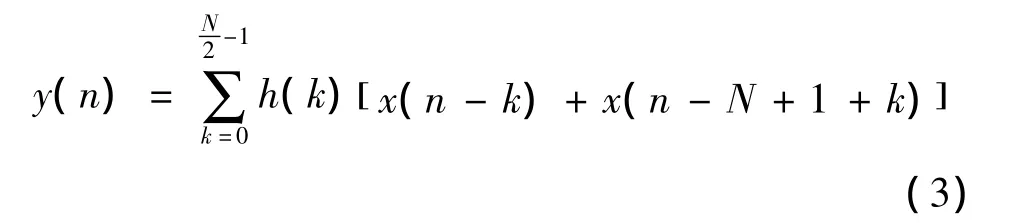
由上式可知,利用它的对称形式比直接实现少用了一倍的乘法器,大大减少了逻辑设计的复杂度和资源用量,节省了费用,因为硬件乘法器是很昂贵的。
1.2 信号抽取的结构优化
对连续信号x(t)进行间隔为T1的采样,得到时域离散信号x(n1T1)。当信号的采样率远大于两倍信号带宽时,可通过抽取过程降低信号的采样率。离散信号x(n1T1)的M倍抽取过程就是每隔M点保留一个点数据,抽取后得到的新信号为y(n2T2),其抽样周期为T2,于是有
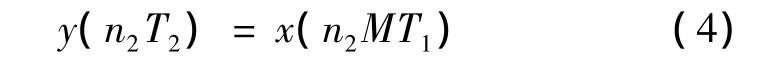
式中:T2=MT1。
若x(t)和y(n2T2)的傅里叶变换分别是X(jΩ)与 Y(ejΩT2),则
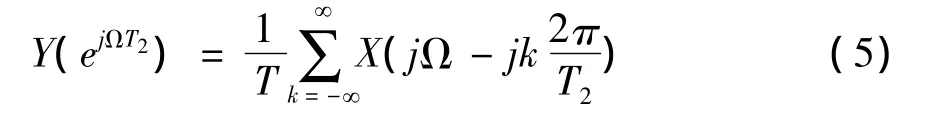
由式(5)可知,为了使得M倍抽取后信号频谱不发生混叠,要求信号带宽小于π/M。在实际信号处理过程中,信号带宽不一定满足这个要求,为了防止混叠,一般要进行抗混叠滤波,即在信号抽取之前进行低通滤波。
令h(n)是一个FIR滤波器的单位抽样响应,长度为N,对M倍的抽取器,可按图1来实现。但这种实现方法效率很低,因为h(n)工作在高抽样率状态,x(n)的每一个点都要和滤波器的系数相乘,但每M个点只要一个,因此有较多的乘法浪费。可通过等价信号流图得到更加有效的优化结构,如图2所示,乘法和加法的次数减少到图1的1/M,这样,y(n)和x(n),h(n)的关系[5]
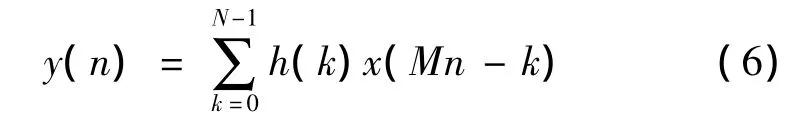

图1 抽取的直接实现
1.3 应用流水线技术的优化
流水线技术在数字电路设计中是为了提高系统的工作时钟频率而采用的一种特殊的设计方法。由于FPGA具有丰富的寄存器资源,因此在FPGA中可以很容易实现多级流水线技术[6]。
FIR滤波器的整个运算包括移位、乘法和加法。在并行FIR滤波器中这些运算在一个时钟内完成,但由于运算逻辑相当复杂,信号延迟较长,从而限制了时钟频率的提高。当整个运算采用流水线结构时,把在一个时钟内欲完成的运算化成若干个子运算,各个子运算采用寄存器输出模式,这样既缩短延时路径,提高时钟频率,又可以使各个子运算同时进行,提高数据吞吐率。对于FPGA器件来说,采用流水线式的设计,可以在不增加电路成本和规模的基础上,有效提高滤波器运算处理的实时性。
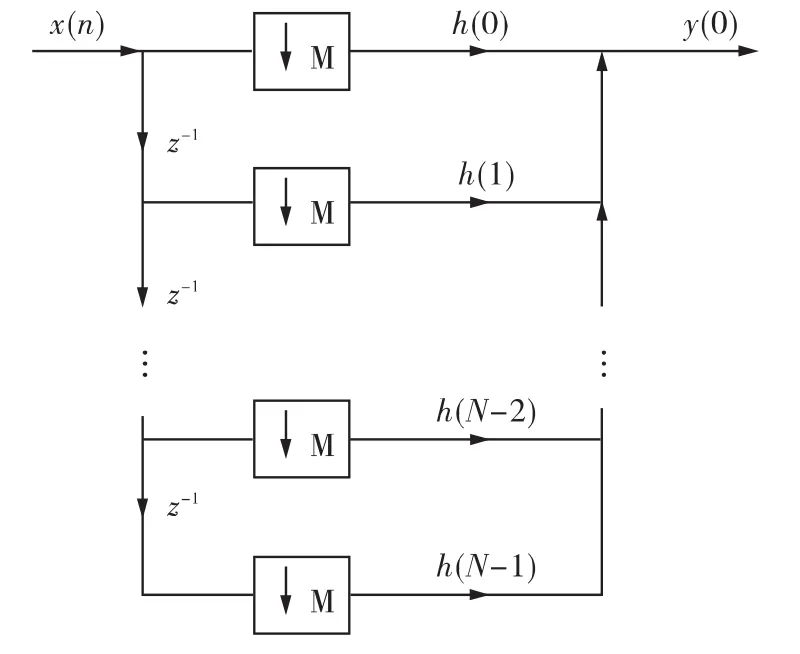
图2 减少乘加次数的优化抽取结构
1.4 多通道的时分复用技术的优化
FPGA设计中的一个重要的思想就是面积和速度的互换。一个设计如果时序余量较大,所能跑的频率远远高于设计要求,那么就能通过功能模块复用减少整个设计消耗的芯片面积,这就是用速度的优势换面积的节约。而时分复用技术就是“速度换面积”思想的一种体现[7]。
基于上述考虑,多通道FIR滤波器的实现采用时分复用的方式。当单通道输入数据的采样频率是f(Hz),对于n通道数据,则提高FIR滤波器模块的工作频率为n×f(Hz)。从而通过高速模块的复用,就可以将需要n个并行FIR滤波器才能实现的设计简化为一个高速FIR滤波器,这样就能在不影响系统速度的前提下大大节省FPGA芯片内部的资源。时分复用技术的设计示意框图如图3所示。
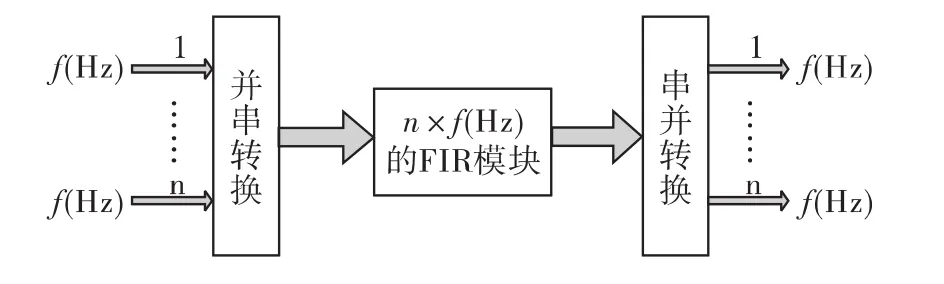
图3 时分复用技术设计示意图
2 多通道抽取FIR滤波器的FPGA高效实现
应用各项优化技术,整个多通道抽取FIR滤波器的高效实现结构框图如图4所示,主要由2部分组成:多通道抽取FIR滤波模块;时钟模块。
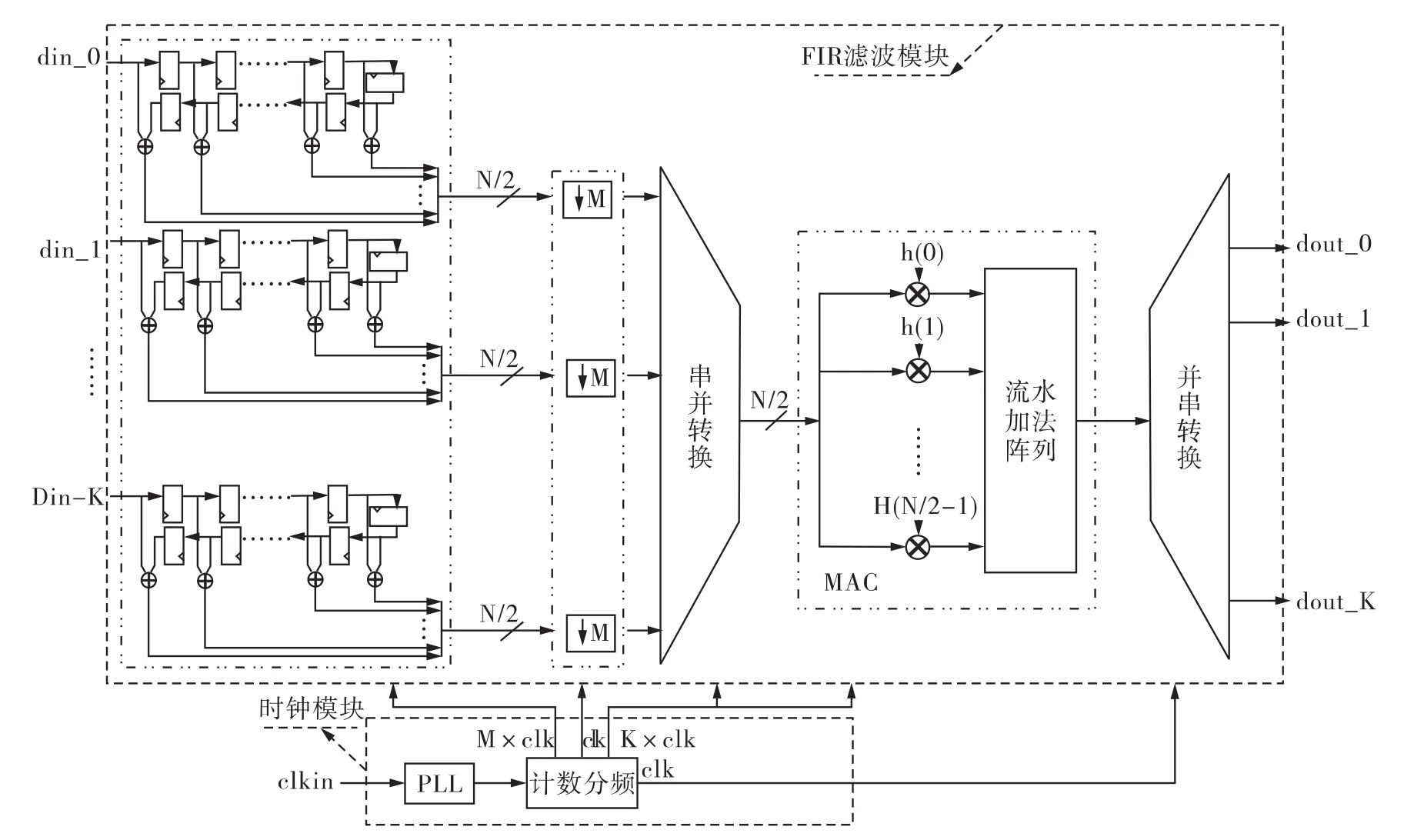
图4 多通道抽取FIR滤波器的高效实现结构
2.1 多通道抽取FIR滤波模块
该模块是整个系统的核心模块,包含以下部分:延迟线单元、两输入加法单元、抽取单元、并串转换单元、乘法器单元、N/2输入加法阵列单元(N为滤波器阶数)、串并转换单元。
K通道数据同时并行输入,根据线性相位FIR滤波器的对称结构,各通道分别同时进行延时和加法操作,使每通道数据输出都由N路减少为N/2路。然后根据抽取的优化结构,输出数据与系数相乘之前就进行M倍抽取,使数据的传输速率也就是系统的速率降低为原来的1/M。接着利用时分复用技术,K通道数据复用一个内部频率是输入数据频率K倍的高速乘加模块,也就是说,一个输入数据时钟周期包含了K个内部时钟周期,于是一个输入数据时钟周期就完成了K通道各一次数据的滤波,这样既大量地节省了FPGA资源,又充分利用了FPGA内部乘法器和加法器的高速性能。由于流水线结构能提高系统的吞吐量率,因此在整个滤波器内插入多级流水结构,主要是在两输入加法、抽取、乘法器和加法阵列之间加入寄存器实现,具体多少级流水可根据系统对速度和资源的要求而平衡决定。最后对乘加单元输出数据进行串并转换后输出K通道滤波数据。
FIR滤波器模块的并行乘法器以及加法器采用FPGA提供的宏单元实现,并指定占用片上内嵌的硬乘法器资源。
2.2 时钟模块
由于系统中需要多种同步的不同频率时钟,所以需由一个时钟模块对整个系统的时钟进行控制。由图4所示,假设以M倍抽取时钟clk为基准时钟,则系统中还需要的时钟有:延迟线和两输入加法器的M ×clk、并串转换和乘加模块的K×clk。
时钟模块的结构:通过一个Altera FPGA内嵌的PLL(Phase Lock Loop,锁相环),将输入的低频率时钟转换为高频率时钟,然后对该高频率时钟进行计数分频得到系统需要的所有时钟,这样得到的所有分频时钟都是同步的。
3 设计的仿真与验证
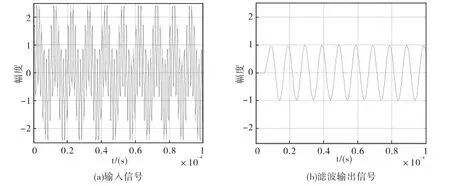
图5 理论结果(MATLAB输出)
本设计采用VHDL语言进行RTL级的描叙,在Quatus II 6.0的环境下进行语言的编译、逻辑的综合以及布局布线,利用MATLAB和ModelSim SE 6.1b进行联合仿真,采用Altera公司的Cyclone II系列EP2C50U484I8芯片实现。
FIR滤波器的具体参数如下:8通道14位数据并行输入,数据采样频率为10MHz,进行10倍抽取,滤波后数据1MHz输出,阻带最小衰减70dB,滤波器阶数是127阶。系数根据引起的频率响应的偏移不大于0.001,即-60dB的要求,确定的量化字长是16位。
时序仿真验证时,不失一般性的引出通道1(0~7共8通道)进行验证,其他通道也就相应得到验证,为了检验设计中采用的优化技术,MATLAB仿真时不采用任何优化措施。FIR低通滤波器的截止频率为250kHz,仿真的输入信号是频率分别为100kHz和700kHz的混合正弦波,如图5(a)所示。输入信号经理想抽取FIR滤波器后的理论结果(MATLAB输出结果)与FPGA实现的抽取FIR滤波器的结果(ModelSim输出)分别如图5(b)和图6所示。对比可知,本设计结果与理论结果输出一致,都是100kHz的单一正弦波,滤波正确,表明设计完全符合要求。
对于本文所述的8通道10倍抽取127阶FIR滤波器,表1给出了未使用优化技术设计的FPGA资源实现和本文使用优化技术设计的FPGA资源实现的结果比较。显然采用本文的优化设计方法,通过复用一个高速乘累加模块,大大减少了FPGA的占用资源,特别是大大减少了昂贵的乘法器资源,而且通过抽取实现的优化,在资源大大减少的情况下,系统的工作速度并没有增加,使多通道抽取高阶FIR滤波器在系统速度要求较高的情况下能够在单片FPGA上实现。
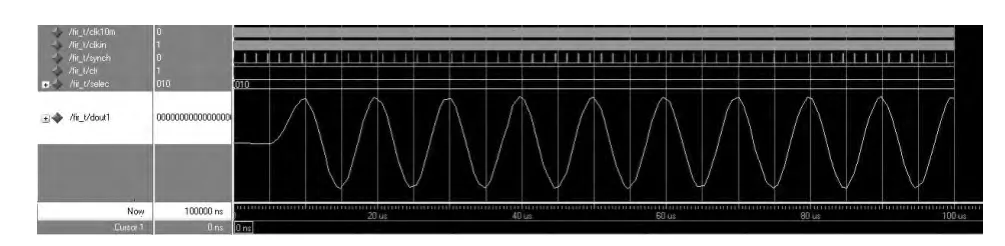
图6 本设计结果(ModelSim输出)
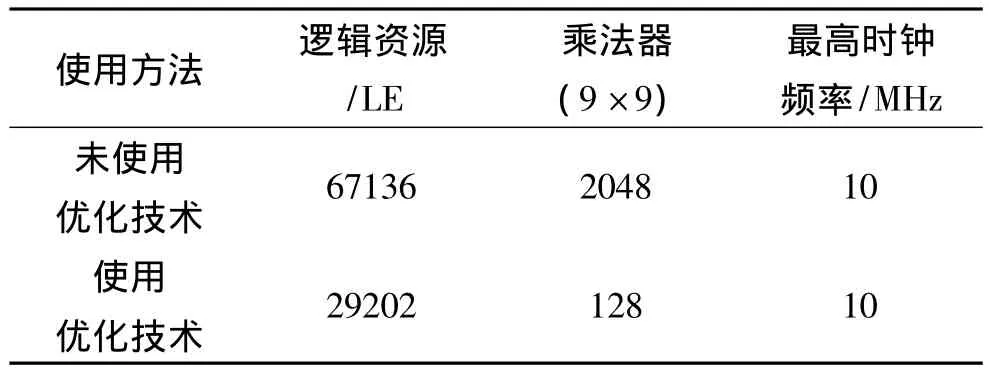
表1 两种实现方法所占FPGA的资源比较
4 结语
对多频连续波雷达的差频点直杂波抑制、抗混叠滤波、降采样和多通道并行输入等各方面要求综合考虑后,设计了一个多通道抽取FIR滤波器,采用了一系列优化措施如滤波器的对称结构、抽取的优化、流水线和时分复用技术等对该滤波器进行了优化设计,使其在作速度没有增加的基础上,节省了大量的FPGA资源,对于工程实现具有显著意义。
[1] 郭联合,王东进.毫米波连续波雷达载波泄漏对消[J].现代雷达,2001,23(4):41-44.
[2]顾红,李玺,等.解决连续波雷达泄漏的一种新途径——周期方波断续法[J].电子学报,1998,26(12):7-11.
[3]江志红,袁俊泉,等.一种新的多频连续波雷达数据采集系统设计[J].现代雷达,2006,28(3):51-54.
[4]Uwe Meyer-Baese.数字信号处理的FPGA实现[M].北京:清华大学出版社,2003.
[5]胡广书.数字信号处理理论、算法与实现[M].北京:清华大学出版社,2004.
[6]王沁,李占才,齐悦.基于两层流水线结构的FIR滤波器设计[J].电子学报,2005,33(2):367-369.
[7]吴继华,王诚.Altera FPGA/CPLD设计(高级篇)[M].北京:人民邮电出版社,2005.

