一体化永磁同步电动机泵控制研究

马升潘，骆光照，唐文明，方学礼

(西北工业大学，陕西西安710129)

0 引 言

随着现代科学技术的发展，超高音速飞行器的发展已成为各国关注的热点。特别是X－51飞行器的成功试飞，智能电动燃油泵作为超燃冲压发动机供油系统的核心装置［1］，要求其能够在系统参数摄动及外部扰动不确定的情况下依然能够对泵的出口燃油进行实时闭环精确调节。

目前航空发动机的主燃油泵多采用固定排量的齿轮泵，齿轮泵的转速与发动机转速直接相关，使得在一些飞行姿态上提供过量燃油，多余燃油重新流回油箱造成燃油温度升高，又需要额外提供配套的冷却系统［2］。

新型高性能战机(如F22、F35)采用基于稀土永磁电机的智能电动燃油泵，这类燃油泵系统可根据发动机转速灵活调整供油量，但是由于无刷直流电动机与开关磁阻电动机的自身转矩脉动较大，转速调节精度较低，从而对燃油泵出口压力、流量的调节精度及实时性产生一定的影响。

永磁同步电动机相对于无刷直流电动机与开关磁阻电动机能够实现在大范围的调速中保持高精度、高动态性能等优点。本系统采用柱塞泵与永磁同步电动机的一体化设计结构，将传统动密封问题转换为静密封问题，大大降低了设计及制造难度，同时显著提高了系统的功重比及功率体积比。耦合后的电机泵数学模型变得更加复杂，高速高空环境下存在很多影响负载特性的因素如振动、摩擦、温度、气压、外界天气参数的扰动等，进而影响对输出油量的控制，使飞行过程受到影响。传统的PI控制在负载变化下具有一定抗干扰能力，但在一定范围内对于系统模型及参数时变的反应能力不足，易造成控制性能的下降，难以满足电机泵对出口燃油的高精度控制要求。滑模变结构控制对电机泵数学模型精度要求不高，对参数及外部扰动的不确定性变化具有一定的自适应性和鲁棒性，响应速度快，同时具有算法简单、便于工程实现的特点，因此提出滑模变结构矢量控制策略以改善电机泵控制性能。并通过基于TMS320F2812与智能驱动模块2SD315A构成的电机泵控制系统平台进行验证，力求控制器高效可靠。

1 系统模型

1.1 一体化电机泵

永磁同步电动机与柱塞泵一体化设计结构如图1所示。

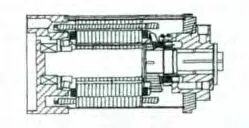
图1 一体化电机泵

将永磁同步电动机转子作为泵缸体，将柱塞泵体集成在永磁同步电动机转子中，使泵体和电机成为一个整体。其中柱塞泵的流量特性:

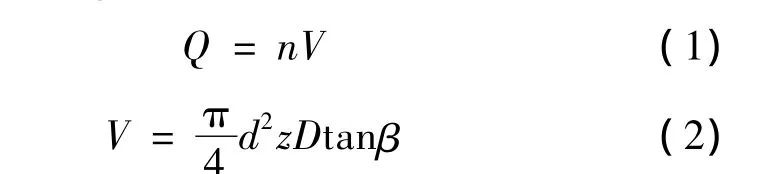
式中:V为泵的排量;z为柱塞数量;d为柱塞直径;D为柱塞回转直径;β为斜盘倾角;n为转子转速。

由式(1)、式(2)可以看出，通过改变电机转速实现对泵出口油量的无级变量调节。

1.2 一体化电机泵模型

一体化电机泵采用隐极式永磁同步电动机。在不计电机磁路饱和及磁滞、涡流损耗影响的情况下，伺服系统采用id=0的永磁同步电动机转子磁场控制。

永磁同步电动机电压方程:

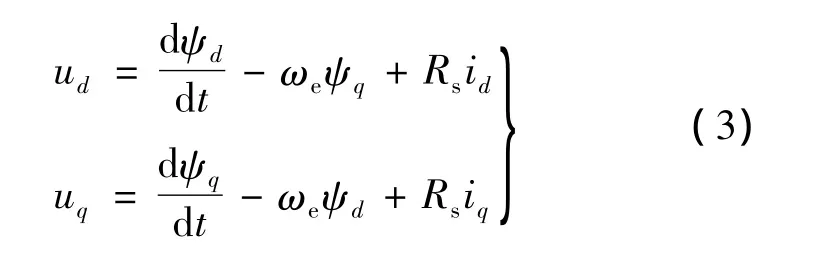
磁链方程:

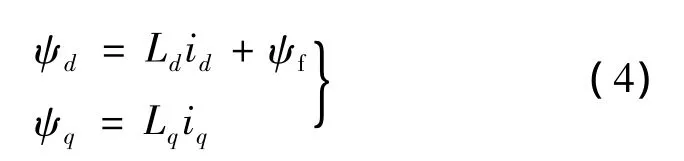
永磁同步电动机电磁转矩方程:

一体化电机泵的运动方程:

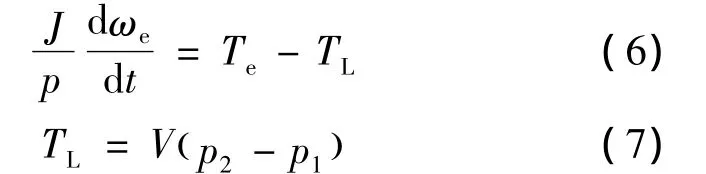
式中:i为d、q轴电流;u为d、q轴电压;Rs为电机泵定子相电阻;L为等效d、q轴电感;p为极对数;ψf为永磁体磁链;ωe为电机泵转子电角速度;J为折算到电机轴上的总转动惯量;B为粘滞摩擦;TL为柱塞泵负载;V为泵的排量;p2为泵的出口压力;p1为泵的进口压力。

在实际运行高空高速的工况下，电机泵会随飞行器高度和速度变化由预增压泵对进出口油压p1、p2进行调整，从式(7)可以看出，这会造成负载转矩的变化，同时永磁同步电动机的系统参数也会随高空高速环境发生变化，从而造成结构耦合后的电机泵的系统模型及参数时变更为复杂。

2 趋近律滑模速度控制器设计

电机泵是速度闭环控制系统，考虑到系统运行要求动态响应速度快的特点，需要对电流同时进行闭环控制。速度环控制器采用滑模变结构算法进行控制，以给定转速与实际转速的差值作为输入，速度环控制器输出则作为电流环调节器的参考给定电流iq输入，电流环调节器采取抗积分饱和PI控制。

2.1 传统等速趋近律滑模

传统等速指数趋近律，如下。

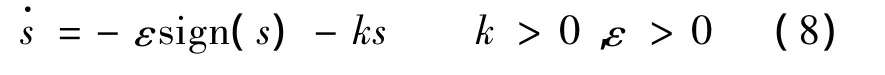
式中:k，ε为可设定的变指数趋近律参数。s为滑模面;－ks为指数趋近项，指数趋近项趋近速度随s变化由一较大值逐渐降低至0，不能保证有限时间内到达滑模面，而等速趋近项εsign(s)在s接近于0时，由于趋近速度s并不为0，能够保证在有限时间内到达滑模面。指数趋近律其切换带为带状，使得系统在切换带运动过程中趋近于原点附近的一个抖振，该抖振会激发系统建模中未考虑的高频成份，使控制器负担加重［3］。

2.2 改进型变速趋近律滑模速度环控制器

针对传统等速趋近律响应速度较慢及抖振现象，对一般等速趋近律进行如下改进。

取系统的状态变量:

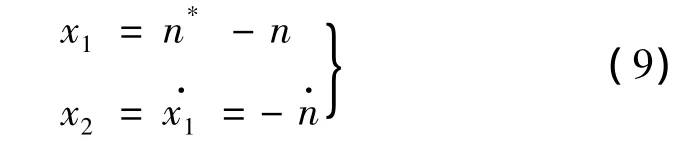
式中:n*为电机泵给定转速;n为电机泵实际转速。

为使系统无超调达到稳定状态，选取一阶滑模面:

式中:c为可设定的一阶滑模面参数。

改进型变速趋近律:

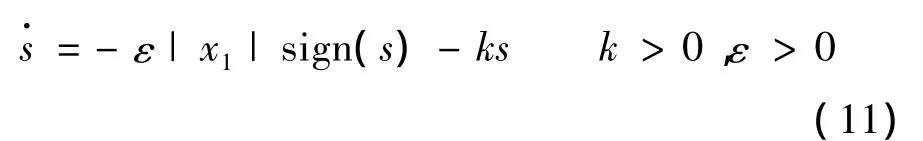
由式(3)～式(6)得:

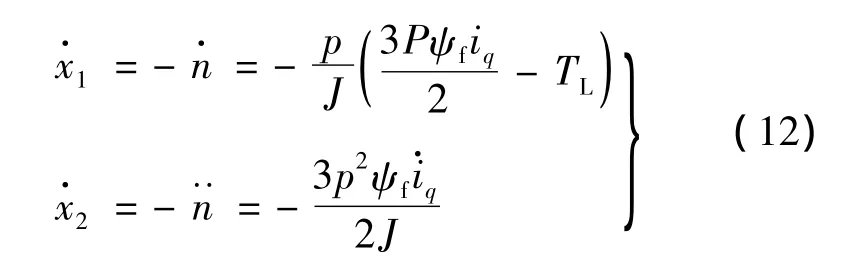
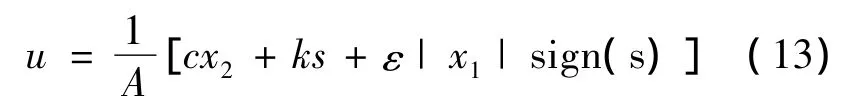
将系统状态变量|x1|引入，从控制器的控制律可以看出，系统状态量在滑模面以外运动时以－ks指数与－ε|x1|sign(s)变速两种趋近速度向滑模面运动，速度大幅提高，指数项在接近滑模面时作用逐渐减弱至0，此时－ε|x1|sign(s)变速项起主要作用，在系统稳定并无限趋向于零的过程中，状态量|x1|进入滑模面并趋向于原点运动，同时控制项－ε|x1|的不断减小使得抖振减弱。采用变速趋近项替换等速趋近项在提高了系统快速性同时也消弱了滑动模态的抖振。

因为:

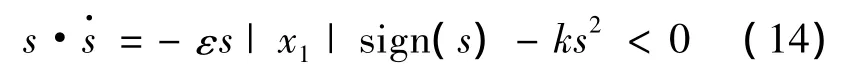
所以，改进型变速趋近律依然满足滑动模态存在性和到达条件。

“边界层”法［4］对滑模控制过程中的抖振现象具有抑制和消除作用。采用饱和函数sat(s，δ)代替控制律中的符号函数sign(s)，其中

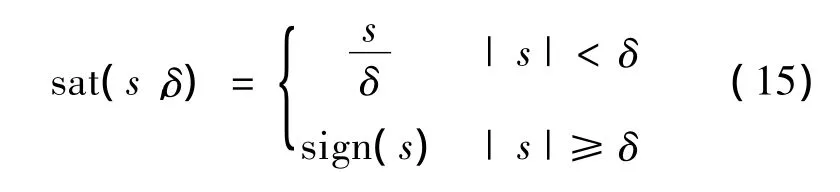
式中:δ为可设定的边界层厚度参数。饱和函数sat(s，δ)使控制在边界层内部由原来的滑动模态上的变结构切换方式变为连续控制方式，进一步消除了滑模面的抖振现象。图2为改进的趋近律控制量iq流程图。

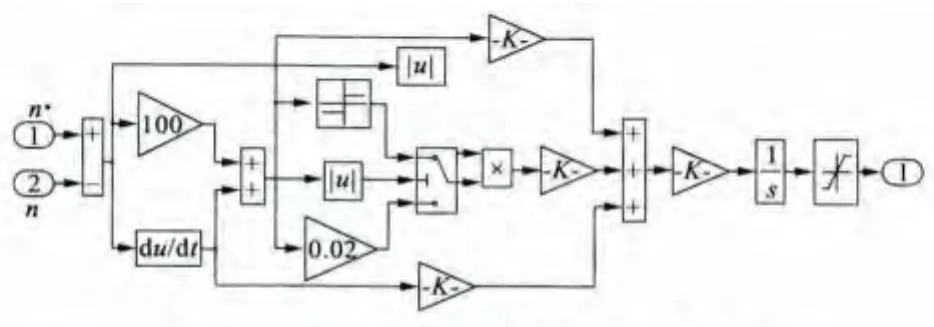
图2 改进的趋近律控制量iq流程图

3 硬件设计

控制器硬件设计功能方案如图3所示。

电机泵控制器实时检测信号多、算法复杂、实时计算量大，系统以TMS320F2812作为主控芯片，通过自身ADC接口采集母线电压、母线电流、冷板温度信号、油泵进出口油压，通过 CPLD操作AD2S1210、AD7357检测转子位置与A、B相电流实时值，并通过地址数据线接口将CPLD采集到的速度信号与相电流信号反馈给DSP以便进行矢量运算并进一步通过事件管理器(EV)发出PWM经光耦隔离后驱动2SD315A来实现对永磁同步电动机的精确控制。

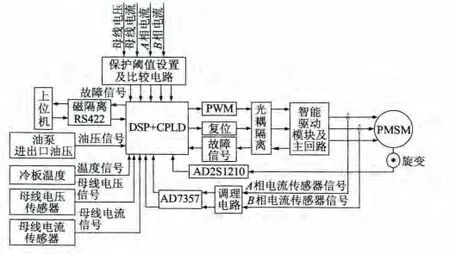
图3 控制器硬件结构图

上位机通过磁隔离通信芯片ADM2587E对控制器进行通信，能够实现实时参数设置及实时状态监测。

4 仿真与实验分析

速度环调节器采用改进型变速趋近律滑模控制(以下简称SMC)，电流环调节器采用抗积分饱和PI控制，id=0矢量控制。系统采用的控制方案结构框图如图4所示。

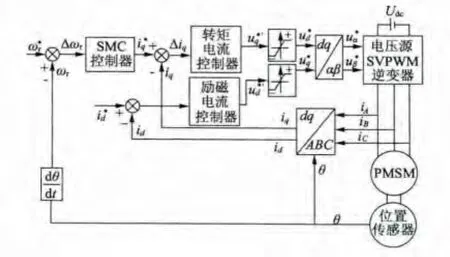
图4 系统控制结构框图

通过MATLAB/Simulink建立包括电机泵和控制器的动态仿真模型。永磁同步电动机参数:极对数2;额定功率15 kW;额定转速11 000 r/min;额定转矩15 N·m;额定电压300 V;定子绕组电阻0.054 5Ω;d、q 轴电感 0.227 mH;转动惯量 J=7.097 ×10－4kg·m2;磁链 ψf=0.061 3 Wb。

仿真参数:转速给定11 000 r/min，负载15 N·m下起动，0.2 s时负载转矩从15 N·m突降至10 N·m。趋近律滑模控制器参数:ε=0.000 5;k=10 000;c=10 000;A=0.001 929;δ=0.02;电流环参数:kp=10;ki=0.5。仿真结果如图5所示。

由图5(a)、图5(c)、图5(e)可以看出，突卸负载时，采用 PI控制，系统转速波动22 r/min，相电流、转矩有较明显的波动，需要一定的调节时间恢复到稳态，且存在稳态误差;从图5(b)、图5(d)、图5(f)看出采用，改进型趋近律滑模控制器，系统转速波动只有3 r/min，相电流、转矩具有较好的动态性能，抗外界扰动能力强，鲁棒性好，稳态精度高。

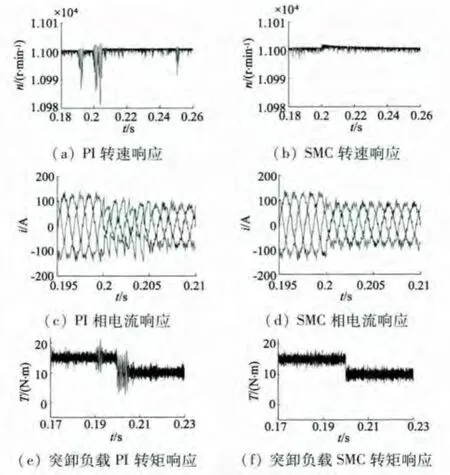
图5 系统突卸负载时动态响应仿真结果

电动燃油泵实验平台如图6所示，转速给定11 000 r/min，实验得出的稳态数据如图7所示。

图6 电动燃油泵实验平台

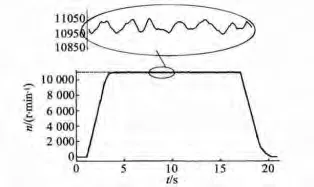
图7 改进型变速趋近律滑模实验波形

由于仿真模型与实际电机模型存在差异，导致实验的结果在数据上不能与仿真完全一致，但是从图7可以看出，采用改进型变速趋近律滑模变结构矢量控制可以快速无超调到达额定转速，稳态误差在0.5%以内，可有效实现对电动泵的高速高精度控制。

5 结 语

本文针对一体化柱塞式电动燃油泵的复杂控制模型，为提高泵用永磁同步电动机调速系统的稳态品质及抗扰动能力，在分析了常规等速趋近律滑模变结构控制后，进一步提出一种改进型变速趋近律滑模控制，仿真结果表明该趋近律可以有效抑制滑模固有的抖振现象，在保证了稳态精度的同时提高了系统抗负载扰动能力。本文同时提出了相应的硬件设计，并通过实验验证了其有效性。

［1］孙强，王健，马会民.X－51A超燃冲压发动机的研制历程［J］.飞航导弹，2011(1):67－71.

［2］张绍基.航空发动机燃油与控制系统的研究与展望［J］.航空发动机，2003，29(3):1 －5.

［3］范炳奎，李颖晖，柳艳丽，等.基于新型趋近律的永磁同步电机滑模变结构矢量控制［J］.微计算机信息，2010，26(8－1):42－44.

［4］Slotine J J，Sastry S S.Tracking control of non － linear systems using sliding surfaces，with application to robot manipulators［J］.International Journal of Control，1983，38(2):465 －492.

［5］刘保连，丁祖军，金德飞.一种新型趋近率的无刷直流电动机伺服系统变结构控制［J］.微特电机，2012，40(1):41 －44.

［6］杨前，刘卫国，骆光照.高空电推进系统的积分滑模反演速度控制［J］.电机与控制学报，2012，16(6):50 －56.

［7］杨逢瑜.斜柱塞斜盘式轴向柱塞泵的流量特性［J］.兰州理工大学学报，2011，37(3):60 －64.

［8］童克文，张兴，张昱，等.基于新型趋近律的永磁同步电动机滑模变结构控制［J］.中国电机工程学报，2008，28(21):102－106.