永磁体不同削角的无刷直流电动机分析与试验

陈治宇，黄开胜，田燕飞，陈风凯，何建源

(1.广东工业大学，广东广州510006;2.苇源电机有限公司，广东佛山528300)

0 引 言

近年来，随着无刷直流电动机应用的电压及功率范围的扩大，在交流供电的家用电器中的应用已经越来越受到人们的关注，为了满足家用电器的新需求，对无刷直流电动机的齿槽转矩、电磁噪声、运行性能等提出了新的要求。因此，本文对一款存在振动和噪声的用于家用电器设备的无刷直流电动机进行分析与研究。

无刷直流电动机气隙中的磁密决定了感应电动势的波形与幅值，而定子绕组中的感应电动势决定了无刷直流电动机的性能［1］。合理的永磁体形状设计可以有效改善无刷直流电动机的气隙磁场［2］，通过改善气隙磁场波形，减小因各次谐波磁场相互作用所产生的径向力波，降低电磁噪声。

永磁体和有槽电枢铁心之间相互作用产生齿槽转矩，导致转矩波动，进而产生振动和噪声，一定范围内永磁体的边缘削角可以消弱齿槽转矩，还能节省永磁材料，降低成本［3］。因此，本文通过解析法分析永磁体不同削角与气隙磁场、齿槽转矩之间的关系，利用电磁场有限元分析软件Ansys中的Maxwell 2D对永磁体不同尺寸的边缘削角进行对比与分析，找出最佳的削角，并对永磁体削角与无削角的仿真和样机测试结果进行对比研究，验证了本方法的合理性和有效性，为无刷直流电动机性能的改善提供了一定的实用价值。

1 气隙磁场与齿槽转矩的解析法分析

1.1 气隙磁场的解析法分析

在永磁体和空气隙的求解区域内［4］，有:

式中:B1和B2分别为永磁体和气隙的磁感应强度;M为磁化强度;μr为永磁体相对磁导率。

将磁体的磁场和磁化问题非线性化，并忽略磁滞效应和涡流损耗，磁场简化为二维场，则磁场和磁感应强度的关系如下:

式中:H为磁场强度;ν1为磁阻率;ν0为真空磁阻率;M为永磁体的磁化强度。

在分析磁场问题时，对于磁感应强度B与永磁体之间的关系，通常引进位函数作为辅助变量，其中磁感应强度B与矢量磁位A满足:

结合麦克斯韦方程和式(2)，采用矢量磁位B为解位函数，得电机磁场的边值关系如下［5］:

式中的第一个式子为求解域内，第二个式子为定子外圆边界，Jc为电枢绕组电流密度。

式(4)等价变分再进行有限元离散，建立以矢量磁位A为未知量的非线性方程组，采用牛顿－拉菲森迭代法求解，计算出各节点的矢量磁位，最后求出区域中的磁场分布。由上述公式可知，通过永磁体边缘削角，改变永磁体形状，即可改善气隙磁场。

1.2 齿槽转矩的解析法分析

无刷直流电动机电流为零时，永磁体与铁心之间相互作用产生齿槽转矩，是电机磁共能W相对于位置角α的导数:

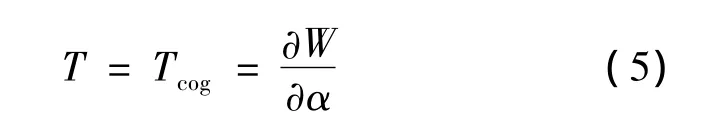
假设电枢铁心导磁率无穷大，同一转子上永磁体的磁极形状、尺寸、性能相同，且磁导率与空气相同，即:

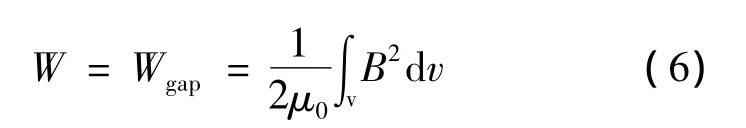
对任意相对位置α，气隙径向磁通密度［6］:

式中:Br(θ)为永磁体剩磁沿圆周方向的分布;g(θ，α)为磁极中心线与齿中心线夹角为α时的有效气隙长度沿圆周方向的分布;hm为永磁体充磁方向长度。则式(6)表示如下:

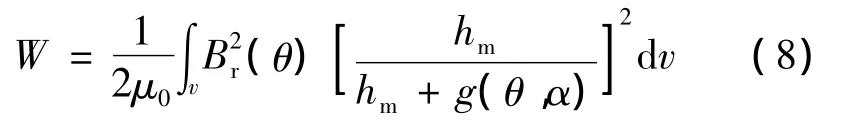
对进行傅里叶分解，进而得到齿槽转矩，即:

式中:p为极对数;Z为槽数。将式(9)、式(10)代入式(5)、式(8)，则齿槽转矩的表达式如下:

式中:LFe为电枢铁心长度;R1为电枢外径;R2为定子轭内径;n为使为整数的整数。从式(11)可知，齿槽转矩只与(θ)有关，通过永磁体边缘削角，使得(θ)减小，消弱(θ)高次谐波，进而削弱齿槽转矩。

2 永磁体削角设计

本方案电机的主要技术参数如表1所示。

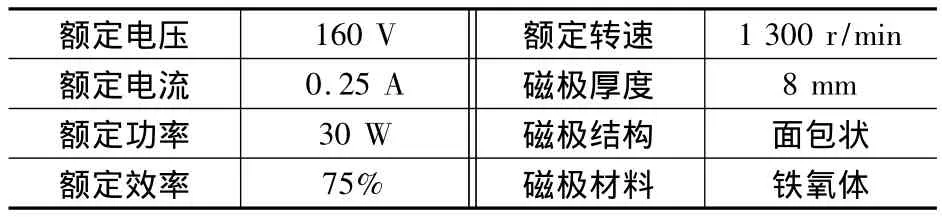
表1 无刷直流电动机主要技术参数

结合以上分析，本文以永磁体厚度为8 mm、宽度为14 mm、结构为面包状、径向充磁的12槽8极无刷直流电动机为例，提出永磁体削角方式，如图1所示，具有两个自由度，通过改变永磁体边缘a、b的值，即可得到不同程度的削角永磁体。

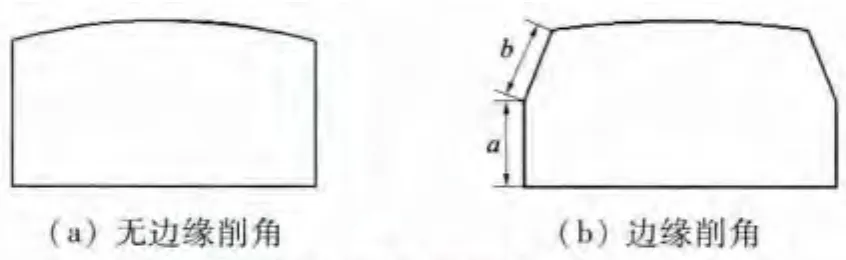
图1 永磁体的削角方式

3 永磁体不同削角的对比分析

根据以上的削角方式，分别选取如表2所示的不同的a、b值对永磁体进行边缘削角。

表2 永磁体边缘削角尺寸

3.1 谐波畸变率的对比分析

电机气隙磁场中各次谐波磁场相互作用所产生的径向力波是形成电磁噪声的主要来源，因此降低谐波畸变率，可以减小径向力波幅值。结合表2中的削角尺寸，在Maxwell 2D中建立不同削角永磁体的电机模型，将定子绕组不通电，得到转子磁场波形，再通过傅里叶分解成各次谐波，求出各谐波畸变率与不同削角永磁体的变化曲线，如图2所示。

对比图2中的四条谐波畸变率变化曲线发现，除a=3 mm时谐波畸变率的大小是随b值增大不断增大，其余谐波畸变率并不是随着永磁体削角程度的增大一直增大，而是先减小后增大，存在一个临界削角位置。根据图2中所有削角尺寸对比分析发现，当a=6 mm，b=2.5 mm时，谐波畸变率最小，其值为14.6%。

图2 永磁体不同削角时的谐波畸变率变化图

3.2 齿槽转矩的对比分析

齿槽转矩会影响电机低速运行和控制性能，而不同程度的永磁体削角能有效消弱(θ)的次谐波分量的幅值，从而改善电机齿槽转矩的大小。所以本文根据表2中的永磁体削角尺寸，对不同削角的齿槽转矩进行有限元对比分析，如图3所示。

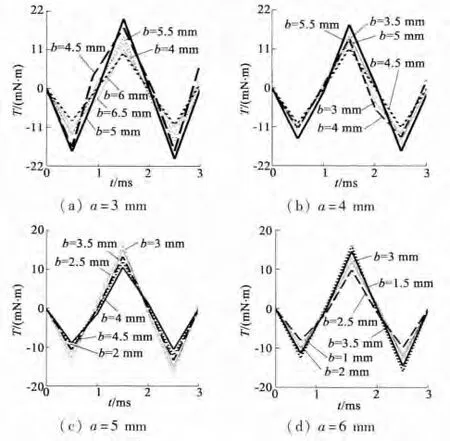
图3 永磁体不同削角时的齿槽转矩对比图

根据以上永磁体不同削角齿槽转矩对比曲线可知，图3(a)中，当b=6 mm时齿槽转矩的幅值最小，为10.07 mN·m;图 3(b)中 b=4.5 mm 时齿槽转矩最小，为11.19 mN·m;图3(c)中b=4 mm时齿槽转矩最小;为10.08 mN·m;图3(d)中 b=2.5 mm时齿槽转矩最小，为9.87 mN·m。

由以上结果可知，对于不同的a值，对应的b值都存在临界的削角位置，当削角超过临界位置时，齿槽转矩的削弱效果反而会变差。故结合以上不同削角尺寸的谐波畸变率和齿槽转矩，发现当a=6 mm，b=2.5 mm时为最佳削角尺寸，对应的谐波畸变率和齿槽转矩最小，其中谐波畸变率为14.6%，齿槽转矩为9.87 mN·m。

4 样机制作与试验验证

根据以上有限元计算分析的永磁体最佳削角尺寸，制作了样机如图4所示，并与图5的永磁体无削角样机进行对比分析。

图4 永磁体最佳削角样机

图5 永磁体无削角样机

为了验证有削角与无削角的永磁体对电机性能的影响，分别进行了有限元分析，并利用测功机对削角永磁体与无削角永磁体的样机进行了测试，测试结果如表3所示。

表3 削角和无削角永磁体样机对比值

从表3可以看出，采用永磁体削角，能有效减小谐波畸变率，削弱齿槽转矩，但由于永磁体削角后导致永磁体的相应减少，使其效率比无削角永磁体的电机降低1.6%;但是在相同转速下，采用削角永磁体的电机比无削角永磁体的电机运行更平稳，性能更好。

由于无刷直流电动机应用于家电设备中，相比效率而言，对电机的振动和噪声要求更高，故综合以上分析，永磁体最佳削角尺寸 a=6 mm、b=2.5 mm。样机定、转子如图6所示。

图6 样机定、转子图

5 结 语

本文根据解析法推导出永磁体削角与气隙磁场和齿槽转矩之间的关系，通过对永磁体不同削角模型的有限元对比分析，研究出不同削角对谐波畸变率与齿槽转矩的削弱情况，找出最佳削角尺寸，并制作了样机。结果表明:

(1)对于永磁体结构为面包状的无刷直流电动机，采用永磁体削角能减小电机的谐波畸变率和削弱电机的齿槽转矩;

(2)不是任何尺寸的削角都能改善电机性能，而是存在一定的削角临界尺寸，当削角程度超过临界尺寸时，改善效果反而会变差;

(3)采用永磁体削角后，电机的效率会比无削角时有所降低，故在工程实践中，可根据实际情况进行选择。

该电机目前已成功应用于一款家用电器设备中，并且批量生产，节能效果明显，受到市场的认可和好评。

［1］陈世坤.电机设计［M］.北京:机械工业出版社，2000.

［2］宋伟，王秀和.消弱永磁电机齿槽转矩的一种新方法［J］.电机与控制学报，2004，8(3):12－16.

［3］辛懋，韩力.削角磁极抑制永磁电动机齿槽转矩的研究［J］.微特电机，2008，36(9):5－8.

［4］王秀和.永磁电机［M］.北京:中国电力出版社，2007.

［5］Chen S，Binns K J.Finite element analysis of the magnetic field in rare－earth permanent magnet systems with consideration of temperature［J］.IEEE Transactions on Magnetics，1992，28(2):1303－1306.

［6］Ackermann B，Janssen H H，Sottek R，et al.New technique for reducing cogging torque in a class of brushleess DC motors［J］.IEEE Proceecing B，1992，139(4):315－330.