双翼形直线超声波电动机

张健滔，李朝东

(上海大学，上海200072)

0 引 言

直线超声波电动机具有结构简单、无需转换机构直接产生直线运动和驱动力、可控性好、定位精度高、设计样式灵活、易于实现小型化、响应快、断电自锁、无电磁干扰等优点［1－6］。

目前，已有多款直线超声波电动机被研究并提出。周铁英等人提出了基于面内弯曲行波的直线超声波电动机，并将其应用于透镜调焦驱动［7］。董蜀湘等人提出了定子是由四层压电陶瓷片构成的直线超声波电动机，其利用二个正交一阶弯振模态工作［8］。Man－Soon Yoon等人提出了穹隆形的直线超声波电动机，其基于惯性冲击原理工作［9］。美国New Scale Technologies公司设计了基于弯振模态的微型直线超声电机，其尺寸最小一款定子仅为1.55 mm ×1.55 mm ×6 mm［10］。

近年，在便携式电子设备、微型机器人、精密仪器仪表、医疗仪器等领域，提出了体积小、质量轻、结构多样、无需减速、无电磁干扰的微型直线电动机的需求［11－15］。传统的电磁式电机难以满足这些要求，而直线超声波电动机由于其固有的特点，则易于实现这些目标。在该需求背景下，本文提出了一款双翼形直线超声波电动机，并对其运动机理进行分析，制作了原理样机，测试了电机的机械特性。

1 电机结构及工作振动模态

1.1 电机结构

双翼形直线超声电机的结构如图1所示。其定子为一个带双翼的空心圆柱结构，圆孔内加工有内螺纹，双翼的上下表面粘贴有压电陶瓷片，也可只在双翼的上表面或下表面粘贴压电陶瓷片。动子为一带外螺纹的圆柱体，定子与动子通过螺纹配合作用。电机压电陶瓷片的具体布置方式及电信号激励接线方式如图2所示，图中箭头为压电陶瓷片的极化方向，左、右翼压电陶瓷片分别接入具有一定相位差的两相正弦激励信号。在电压的作用下，可激发出电机的工作振动模态，从而定子内螺纹的驱动质点产生椭圆轨迹运动，并通过定子、动子间的接触摩擦力，驱动动子进行旋转直线运动。切换两相交变电压的相位差，即可改变动子的直线运动方向。

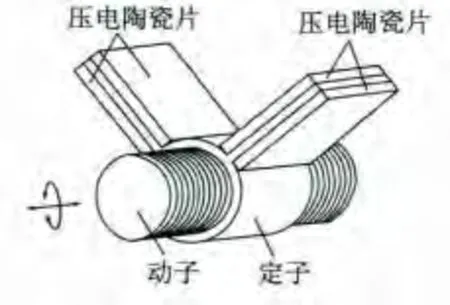
图1 双翼形直线超声电机结构图

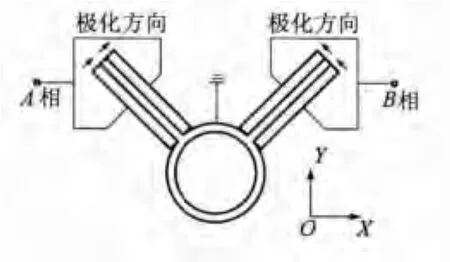
图2 压电陶瓷片的极化方向与布置

1.2 电机工作振动模态

电机工作所需的两个振动模态的振型如图3所示。图3(a)的工作振动模态的特点:定子双翼向同一侧同时弯曲振动，空心圆柱前后两端左右摆动。其中双翼向右侧弯曲时，空心圆柱前后两端向左运动;双翼向左侧弯曲时，空心圆柱前后两端向右运动。图3(b)的工作振动模态的特点:定子双翼同时向相反方向弯曲振动，空心圆柱前后两端上下摆动。其中左翼向左侧弯曲而右翼向右侧弯曲时，空心圆柱前后两端向上运动;左翼向右侧弯曲而右翼向左侧弯曲时，空心圆柱前后两端向下运动。

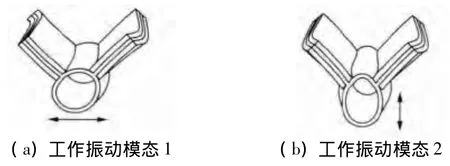
图3 电机定子的工作振动模态

2 电机工作原理

当给图2的A相信号输入端接入正弦电压信号E0sin(ωt)，激励频率接近于电机定子的工作模态频率，将激励出电机工作模态1，此时，定子驱动质点沿x轴向的位移响应可表示:

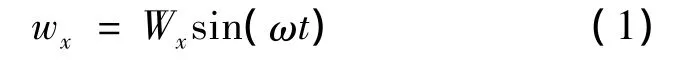
式中:Wx为驱动质点沿x轴向的位移响应幅值;ω为电机激励电压圆频率。

当给图2的B相信号输入端接入正弦电压信号E0sin(ωt+φ)，将激励出电机工作模态2，此时，定子驱动质点沿y轴向的位移响应可表示:式中:Wy为驱动质点沿y轴向的位移响应幅值;φ为相位差。

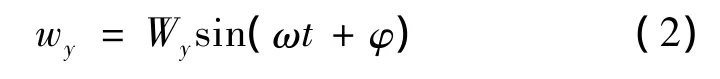
当A、B两相同时激励时，可由式(1)和式(2)得到此时驱动质点的轨迹方程:

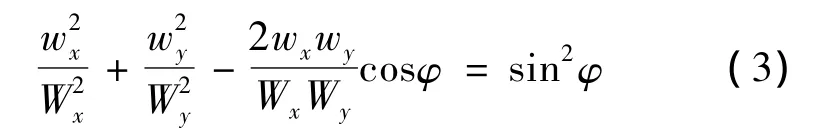
此时，定子驱动质点的运动轨迹为一椭圆，其形状由相位差φ、振幅Wx与Wy确定。

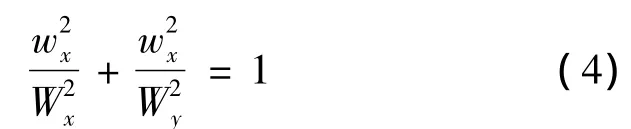
此时，驱动质点的轨迹是顺时针方向形成正椭圆。

通过改变两相激励电压的相位差，即可改变动子的运动方向。当相位差φ=－时，驱动质点的轨迹是逆时针方向形成正椭圆，此时定子驱动动子持续顺时针旋转直线运动。

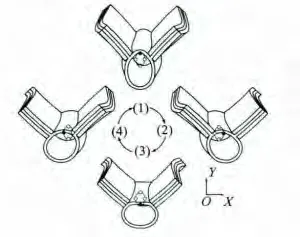
图4 电机工作原理示意图

3 设计与分析

利用有限元分析方法对电机定子进行设计与分析，使用ANSYS建立电机定子的有限元分析模型。定子金属弹性体采用了SOLID45单元，压电陶瓷片采用了SOLID5单元。电机定子主体材料为硬铝，其密度为2 780 kg/m3，弹性模量为70 GPa，泊松比为0.33。压电陶瓷片使用的材料为PZT－8，密度为7 650 kg/m3，泊松比为 0.31，其刚度矩阵、压电应变矩阵和介电常数矩阵分别:

利用所建立的有限元模型对电机定子进行模态分析，并根据定子各结构参数对两工作模态的灵敏度进行分析，调节定子的结构尺寸大小，最终获得两工作模态频率趋于一致的分析结果。两工作模态频率分别为 45.044 kHz和 45.192 kHz。

以45.1 kHz为激励频率、100 V为激励电压峰峰值对定子进行谐响应分析，以分析定子驱动质点的运动轨迹，结果如图5所示。从图5可以看出，定子上四个驱动质点的运动轨迹都是沿逆时针方向运动，此时将能驱动动子沿顺时针方向旋转直线运动。此仿真结果验证了电机运动机理的分析。当改变两相电压信号的相位差，驱动质点的运动方向将改变，同时动子的运动方向也会沿相反方向运动。

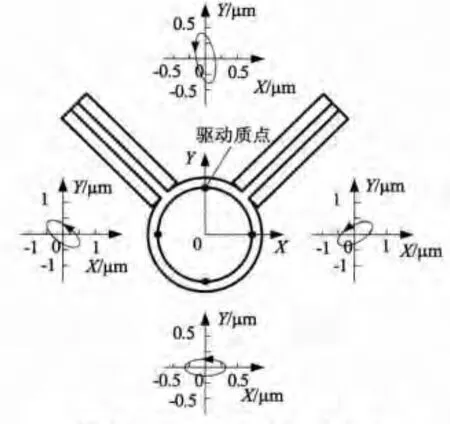
图5 驱动质点的运动轨迹

4 电机试验结果与分析

4.1 电机定子振动特性试验

根据有限元设计与分析的结果，制作了双翼形直线超声波电动机样机，如图6所示。其中，电机定子尺寸小于6.8 mm×9.3 mm×11 mm，压电陶瓷片尺寸为0.5 mm ×4.2 mm ×11 mm。

图6 直线超声波电动机样机

利用PSV－400多普勒激光测振仪对电机定子振动特性进行测试，获得幅频响应曲线和两相振动模态的振型，如图7所示。图7(a)为测试电机定子圆柱体沿X轴方向的振动，即对应图3(a)工作振动模态1，从图3(a)可看出其局部振型应为一阶弯振振型，图7(a)的振动模态振型与分析结果一致。图7(b)为测试了电机定子圆柱体沿Y轴方向的振动，即对应图3(b)工作振动模态2，图7(b)所获得的振型为一阶弯振振型，与图3(b)所示分析结果一致。两相工作模态的频率分别测得为43.218 kHz和43.406 kHz，两工作模态频率一致。从图7(c)可以看出，离A相、B相工作模态最近的干扰模态频率分别为 39.52 kHz、39.515 kHz，工作模态与干扰模态的频率间隔分别为 3.698 kHz、3.891 kHz，该频率间隔足够大以至于干扰模态不会对电机工作产生影响。实测的两相电机工作模态频率比有限元计算频率45.044 kHz和45.192 kHz略有偏低。这主要是由于样机加工误差，材料实际属性与有限元计算使用的材料属性有偏差，以及有限元建模过程中处理金属体与压电陶瓷片结合的方式与实际情况存在偏差。但计算误差是在可接受范围内。

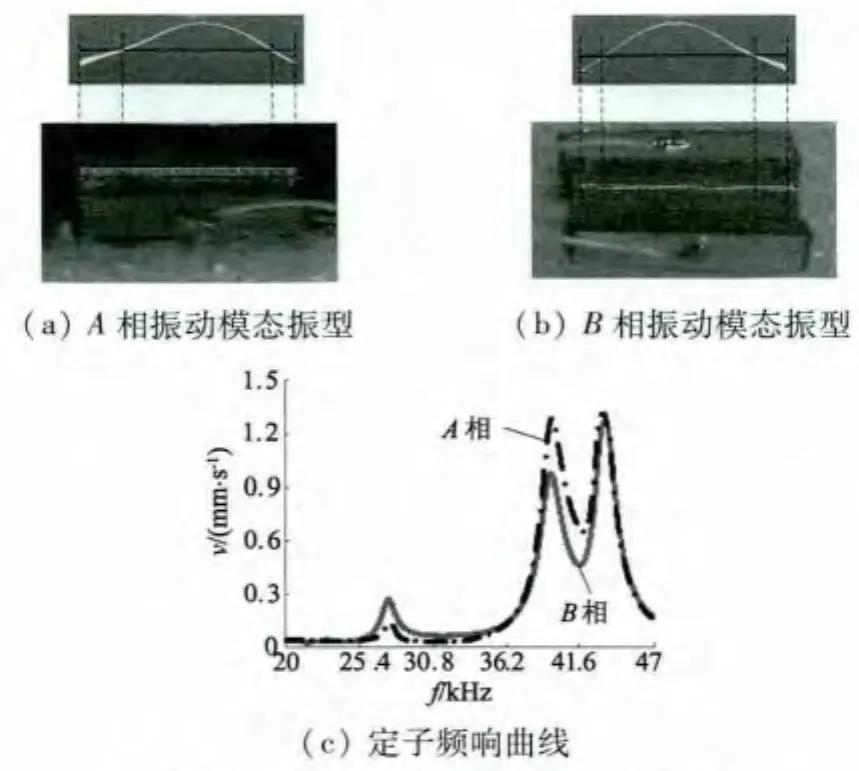
图7 电机定子频响曲线与实测振型

4.2 电机机械特性试验

电机利用信号发生器(Tektronix AFG3022)与功率放大器(HFPA－41)供电，测试其激励频率与速度之间的关系，结果如图8所示，其中激励电压峰峰值为250 V。从图8可以看出，电机可在38.5 kHz～48.7 kHz的激励频率范围内运行，电机速度有一峰值。当驱动频率为43.5 kHz时，电机运动速度最大，为 1.55 mm/s。当驱动频率为 38.5 kHz、48.7 kHz时，电机运动速度较低，分别为 0.35 mm/s、0.15 mm/s。电机的驱动频率范围较宽，通过控制驱动频率即可控制电机的运行速度。

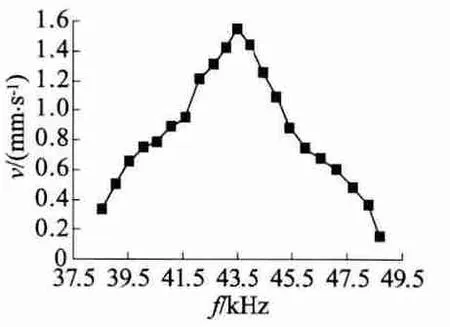
图8 电机激励频率与速度的关系曲线

图9 为电机激励电压与速度的关系曲线图。电机的激励频率为43.5 kHz，电压的峰峰值从80～250 V变化时，电机速度从0.3 mm/s增加到1.55 mm/s。可以看出，通过改变驱动电压即可控制电机的运行速度。

图9 电机激励电压与速度的关系曲线

当电机的激励频率为43.5 kHz、激励电压峰峰值为250 V时，电机输出力与速度的关系曲线图如图10所示。随着输出力的增加，电机速度逐渐减小。空载时电机的速度为1.55 mm/s，当负载为0.106 N时，电机的速度为0.1 mm/s。电机定子的质量为0.9 g，其最大输出力约为定子质量的11.7倍。

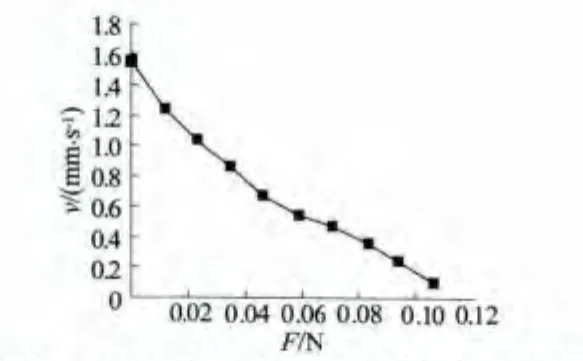
图10 电机输出力与速度的关系曲线

5 结 语

本文介绍了一款新型的双翼形直线超声波电动机。电机定子为一个带双翼的空心圆柱结构，其利用定子双翼弯曲振动致使空心圆柱上下、左右摆动的两个振动模态工作，驱动动子旋转直线运动。研究了电机定子的驱动机理，推导了电机定子驱动质点的运动轨迹方程，理论上分析了电机正/反向运动的工作原理。利用有限元方法对定子进行了分析计算，并对其驱动质点的运动轨迹进行了仿真，验证了电机运动机理分析的正确性。对电机原理样机进行了性能测试，试验表明电机的工作频域范围较宽，在激励电压峰峰值为250 V时，电机的空载速度为1.55 mm/s，最大输出力为0.106 N，是定子质量的11.7倍。该款直线超声波电动机性能可进一步优化，有望能满足小型电子设备、微型机器人、便携式医疗仪器等对微型直线驱动器的需求。

［1］Zhao Chunsheng.Ultrasonic motors technologies and applications［M］.Berlin Heidelberg:Springer－ Verlag，2011.

［2］Szufnarowski F，Schneider A.Two － dimensional dynamics of a quasi－ static legged piezoelectric actuator［J］.Smart Materials and Structures，2012，21:055007.

［3］张健滔，李朝东，何晓菁.卧板式直线超声电机的特性分析模型［J］.中国电机工程学报，2012，32(18):137 －144.

［4］Merry R，Molengraft R，Steinbuch M.Modeling of a walking piezo actuator［J］.Sensors and actuators，2010，A162:51 － 60.

［5］张顺鑫，李朝东.微型化矩形振子近似行波型直线超声波电动机［J］.微特电机，2012，40(2):18 －21.

［6］Wischnewskij W，Wischnewskij A.Piezoelectric actuator for an ultrasonic motor:US，20100013353 A1［P］.2010 －01 －21.

［7］周铁英，陈宇，鹿存跃，等.螺母型超声电机驱动的集成透镜调焦系统［J］.中国科学 E 辑:技术科学，2009，39(10):1650－1654.

［8］Li Xiaotian，Chen Zhijiang，Dong Shuxiang.A double B1 － mode 4－ layer laminated piezoelectric linear motor［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2012，59(12):2752－2757.

［9］Yoon M S，Khansur N H，Lee K S，et al.Compact size ultrasonic linear motor using a dome shaped piezoelectric actuator［J］.Journal of Electroceramics，2012，28:123 －131.

［10］Xu Qin，David A H，Piazza D.Reduced － voltage，linear motor systems and methods thereof:US，20100039715 A1［P］.2010 －02－18.

［11］Cheng Fang，Fan Kuangchao，Miao Jinwei，et al.A BPNN － PID based long－stroke nanopositioning control scheme driven by ultrasonic motor［J］.Precision Engineering，2012，36:485 －493.

［12］Lorenzo D D，Momi E D，Dyagilev L，et al.Force feedback in a piezoelectric linear actuator for neurosurgery［J］.The International Journal of Medical Robotics and Computer Assisted Surgery，2011，7(3):268 －275.

［13］周丽平，孙志峻，张泉，等.一种应用正态分布理论的直线超声电机精密定位控制方法［J］.中国电机工程学报，2012，32(27):60－65.

［14］Kim B，Park S，Park J O.Microrobots for a capsule endoscope［C］//Singapore:IEEE/ASME International Conference on Advanced Intelligent Mechatronics Suntec Convention and Exhibition Center.2009:729 －734.

［15］Lu Haiwei，Zhu Jianguo，Lin Zhiwei，et al.An inchworm mobile robot using electromagnetic linear actuator［J］.Mechatronics，2009，19:1116－1125.