多轴应力状态下混凝土的动态强度准则

王怀亮，宋玉普

多轴应力状态下混凝土的动态强度准则

王怀亮1，2，宋玉普3

（1.大连大学建筑工程学院，116622辽宁大连；2.武汉大学水资源与水电工程科学国家重点实验室，430072武汉；3.大连理工大学海岸和近海工程国家重点实验室，116024辽宁大连）

为了解复杂应力状态下混凝土动态强度变化规律，提出了一个考虑应变率效应的八面体应力空间的多轴静动破坏准则.该准则的空间破坏包络曲面采用二次函数形式，在偏平面上的破坏包络线采用Willam-Warnke模型在偏平面上的椭圆曲线，使用特征应力点法对拉压子午线方程进行修正以考虑偏平面上罗德角对动态强度的影响.通过对大量混凝土多轴静动强度试验成果的分析，表明此强度准则与已有的试验结果吻合较好，能很好地反映平面应力或三轴应力状态下普通混凝土的静动强度变化规律，并且形式简单，便于实际应用.

混凝土；应变率；罗德角；强度准则；特征应力点

随着混凝土结构应用领域的不断扩展，出现了许多形式多样、受力情况复杂的大型混凝土结构，如预应力混凝土压力容器、混凝土重力坝及拱坝、大型海洋采油平台、大型地下工程混凝土衬砌以及巨型框架结构节点核心区等.在这些大型混凝土结构内部，混凝土材料大都处在双向或三向的复杂应力状态.在地震作用下这些结构的内力更为复杂，还需要考虑应变率效应的影响，这些情况下若依然使用单轴拉、压、剪强度理论对工程进行设计和验算，可能会给大型结构的建设和使用带来危险.通过对混凝土单轴动态力学能的研究，发现混凝土材料具有率敏感性［1-3］，即随着应变率的增加，混凝土的动力强度增高，非线性程度随之增加.研究复杂应力状态下混凝土的动态性能更符合工程实际情况，如何反映出在多轴应力组合条件下，混凝土动态强度的变化规律是一个亟待解决的课题.

目前针对单轴动态试验和动态强度准则的研究较多，但由于混凝土多轴破坏准则为非线性，如再考虑应变率的影响，将使其更加复杂化，因此迄今为止，混凝土在多轴应力状态下的动态特性研究还比较少［4-7］，且所得的试验结果离散性较大，只获得了一些定性规律，未见到系统的多轴动态强度准则研究.本文系统分析了混凝土多轴静动态强度变化规律，建立了一个考虑应变率效应的八面体应力空间的多轴静动破坏准则.

1 破坏面方程

三向受力状态下混凝土强度，可用3个主应力为坐标的空间破坏包络曲面表示，如图1所示，根据文献［8-9］的总结，它沿着子午面可以用一个二次方程或一个幂函数来表示.这里在八面体应力空间采用如下形式的极限强度包络面方程:

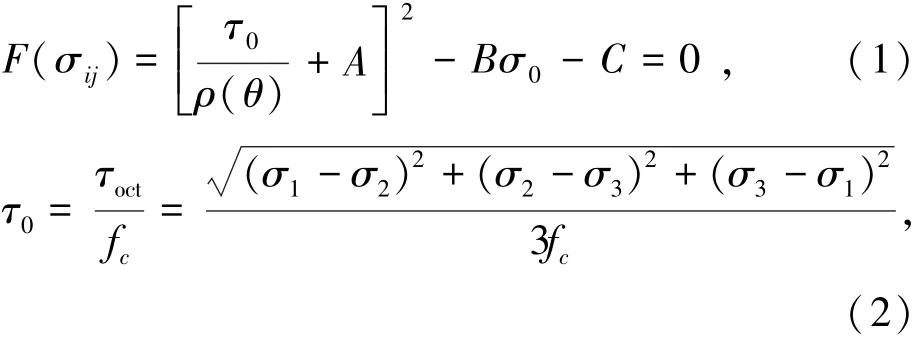
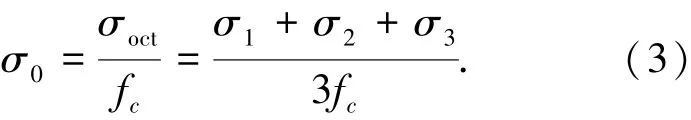
式中:σoct和τoct分别是八面体空间的正应力和剪应力；i=1～3表示沿各坐标轴方向的主应力；A，B，C是待定参数，可用单轴受拉强度（θ=0°）、单轴受压强度（θ=60°）以及双轴等压强度（θ=0°）等特征应力点来确定．

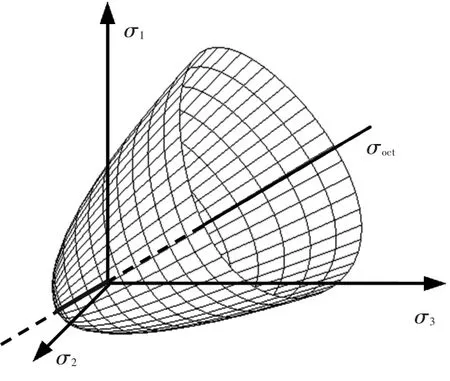
图1 混凝土材料在主应力空间的破坏面

极坐标函数ρ（θ）决定了极限强度包络面在偏平面上的投影形式，它可以采用Willam-Warnke所建议的椭圆曲线方程［10］来表示:

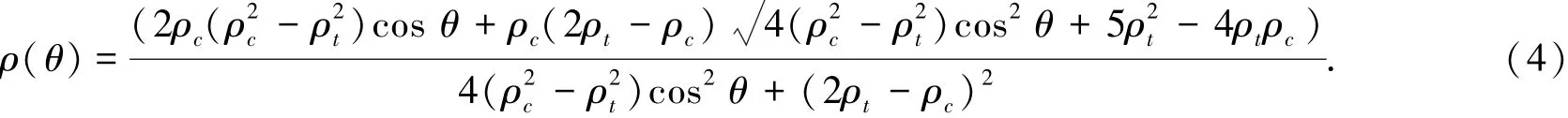
式中:ρt，ρc分别为拉伸和压缩子午线的极半径；上式当ρt／ρc=0.5→1.0时，偏平面包络线由三角形逐渐过渡为椭圆曲线最终变成圆形，另外Willam和Warnke提出的椭圆曲线能够满足偏平面上的破坏包络线对称、光滑和外凸的特征要求，这些都恰好是混凝土在偏平面上的破坏包络线的变化规律，见图2.

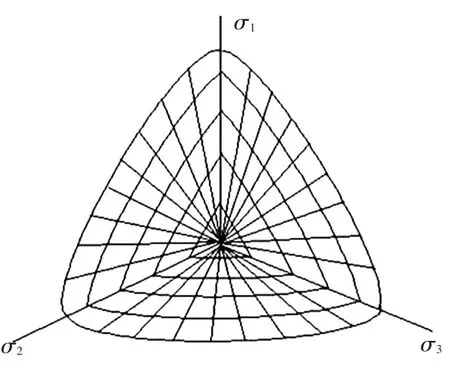
图2 偏平面上的极限强度包络线

拉子午线ρt（θ=0°）上的特征应力点有单轴拉、双轴等压等，压子午线ρc（θ=60°）上的特征应力点有单轴压、双轴等拉等，二者与静水压力轴仅有一个交点，即三轴等拉点．极限强度破坏面方程（1）有3个待定参数，即只需要3个特征应力点就可以确定极限强度面的表达式．在静态应力条件下，当已知某一点的应力状态为（σ1、σ2、σ3）时，可以根据下面的公式将其转化为八面体应力空间的正应力、剪应力以及罗德角，然后代入式（1）即可判断是否达到极限状态．

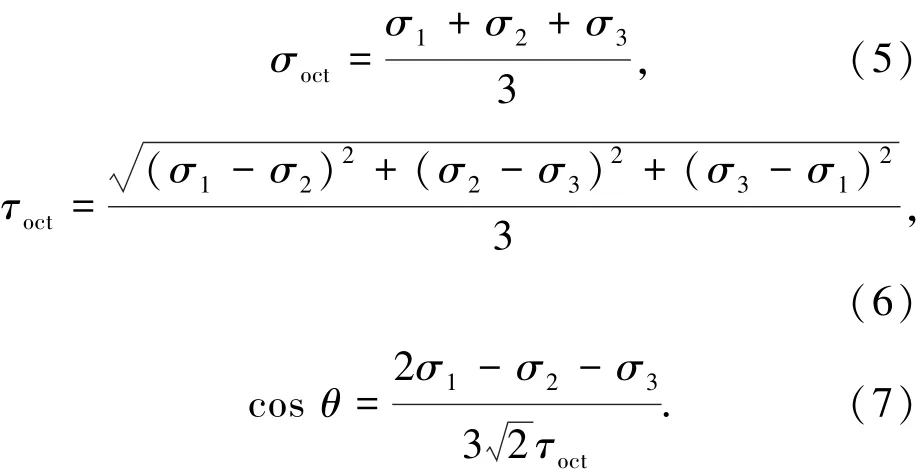
将大连理工大学近几年进行的有关混凝土在多轴应力条件下的强度试验结果（包括三向受拉的试验结果）［11］绘在拉压子午面及偏平面上，见图3、4，发现该强度准则与静态多轴强度试验值符合较好，适用于平面应力、三向受压、三向拉压乃至三向受拉等多种应力状态，且计算简单，便于工程设计和非线性分析应用.

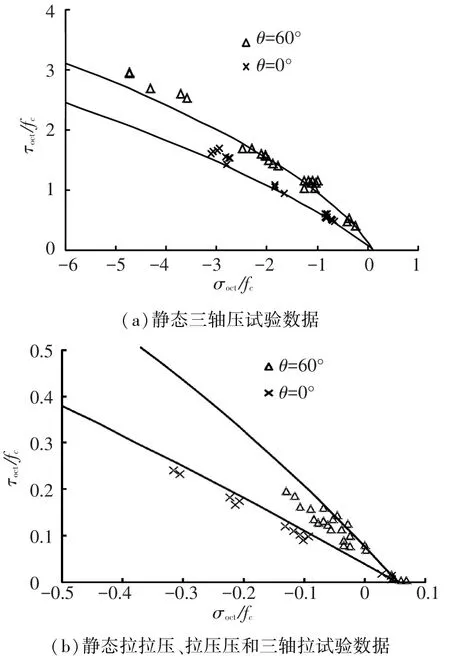
图3 建议破坏准则与混凝土三轴静态试验数据在子午面上的比较

图4 建议破坏准则与混凝土静态三轴试验数据在偏平面上的比较

2 动态破坏面方程的确定

混凝土结构在其工作过程中，除承受多轴静荷载作用外，还承受动荷载作用（如地震作用），且动、静态力学性能之间差异显著，而当前混凝土结构的抗震安全评价中，仅将混凝土静态力学参数提高一个百分比作为动力学参数进行结构抗震安全评价显然不够.因此对混凝土开展多轴应力条件下动态力学特性试验具有极为重要的意义.为了深入了解混凝土的应变速率敏感性对工程结构抗震设计的意义，大连理工大学林皋、闫东明团队以及宋玉普团队分别通过试验研究了混凝土在双向加载以及三向加载条件下的率敏感特性［12-13］.本文基于这些试验数据，确定出普适于混凝土的多轴动态强度准则的材料参数值，需要说明的是，本文研究的应变率范围为10-6／s～1／s，主要考虑了地震作用下的加载速率范围.在这样的加载速率范围内，混凝土材料仍是稳定材料，其应力空间内的破坏面依然具有光滑、外凸的形式，并且其偏平面沿着静水压力轴从近似三角形向近似圆形截面过渡.为了建立混凝土的动态强度准则，进行下面一些约定:

1）混凝土强度关系系数定义约定

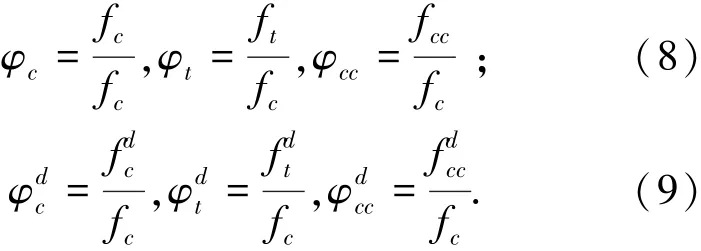
式中:fc、ft、fcc分别是静态加载速率下，得到的静态单轴抗压强度、单轴抗拉强度和双轴等压强度；分别是在动态加载速率下，由试验得出的动态单轴抗压强度、单轴抗拉强度、双轴等压强度，以上数据均可以从试验中得出．

2）混凝土的动态强度放大系数定义约定

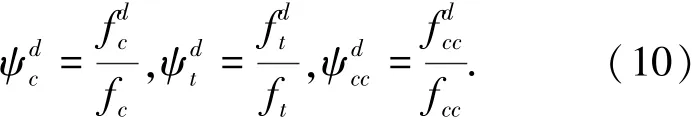
4）拉伸和压缩子午线的极半径ρt、ρc可以通过William-Warnke提供的拉、压子午线方程得到，分别取θ=0和θ=π／3，得出下列表达式:

5）根据以上约定和推导，混凝土在单轴受压、单轴受拉、双轴等压应力状态下的强度表达可以汇总到表1，利用表1所列的3种应力状态可得出A、B、C的具体表达式（14）～（16）．

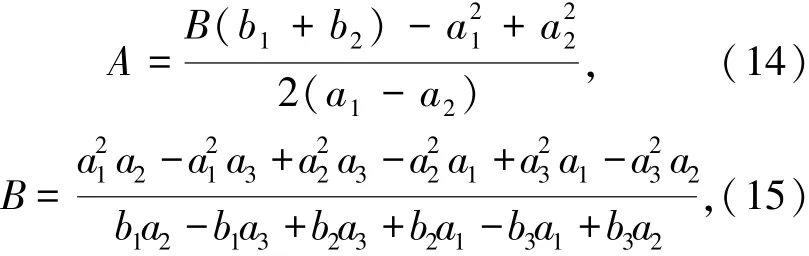
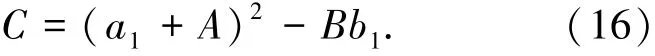
表1 破坏面的特征应力点

混凝土静态强度关系系数根据混凝土材料常规试验得出，对于普通混凝土有

φc=1.0，φt=0.125，φcc=1.16．

3 试验验证

3.1 试验概况

试验主要在大连理工大学海岸和近海工程国家重点实验室的大型静、动三轴电液伺服试验系统上进行.试件采用的规格为100 mm×100 mm× 100 mm立方体试件，混凝土强度等级分别为C20和C30两种.试验中加载应变率的量级分别为10-5／s（设定为静态加载速率）、10-4／s、10-3／s和10-2／s，加载路径主要有以下几种:

1）定侧压下的变速率受压试验和定侧压下的变速率劈拉试验［7，13］:一个方向加载至预设的侧应力值，并保持恒定；另一方向以设定的不同加载速率施加竖向荷载，直至试件破坏.侧应力加载量级分别为0，0.25fc，0.5fc和0.75fc．

2）双轴比例加载试验［12-13］:两个方向按照预设的比例以设定的不同加载速率施加双轴荷载，直至试件破坏.选取5种应力比分别为1∶0、1∶0.25、1∶0.5、1∶0.75和1∶1.

3）三轴恒侧压加载试验［6，12］:试件两个侧面（X，Y方向）加载至预设的侧应力值，并保持恒定；Z方向以设定的不同加载速率施加竖向荷载，直至试件破坏.其中C30混凝土侧应力加载量级分别为0、8、16和24 MPa，主加载面上加载速率量级分别为10-5／s（设定为静态加载速率）、10-4／s、10-3／s和10-2／s.对于C20混凝土侧应力加载量级分别为0、4、8、12和16 MPa，主加载面上加载速率量级分别为10-5／s（设定为静态加载速率）、10-4／s和10-3／s.

4）三轴比例加载试验［6，12］:3个方向按照预设的比例以设定的不同加载速率施加三轴荷载，直至试件破坏.选取4种应力比分别为1∶0.25∶0.1、1∶0.5∶0.1、1∶0.75∶1和1∶1∶0.1.

强度试验结果在子午面上的图形见图5.从试验数据可以看出:随着应变速率的增加，各种应力组合下的混凝土强度均有提高的趋势，其提高的幅度并不相同.

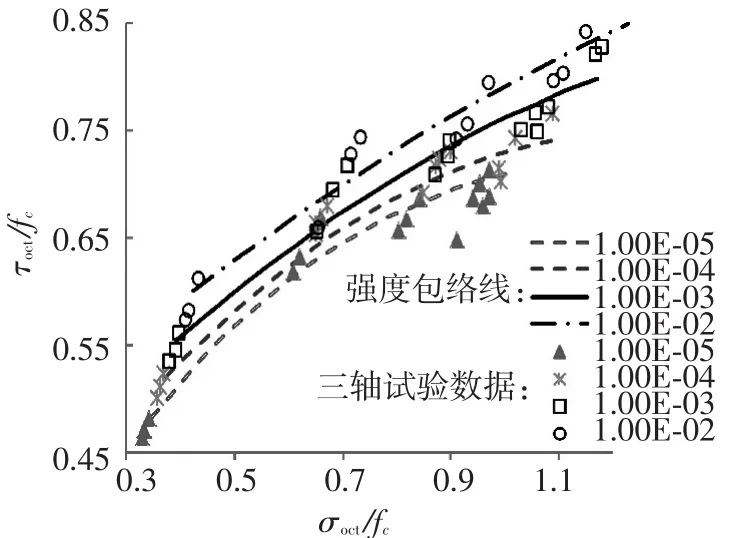
图5 八面体应力空间内破坏准则与试验结果的对比

3.2 确定动态强度准则的材料参数

对于中低强度混凝土在单轴压、单轴拉和双轴等压应力状态下的动力强度增大系数，通过文献［12］试验数据得出:

式中:˙ε表示应变率，变化范围是10-5／s～10-2／s；˙εs表示标准静态应变率，取10-5／s．

3.3 验证三轴动态应力状态

与大连理工大学课题组混凝土多轴动态强度试验数据［12-13］进行对比验证，见图5.在八面体应力空间中，不同应变率下试验数据点与对应的拉压子午线吻合较好，在相同的应变率下，比例加载和定侧压加载两种加载路径下的试验数据基本分布在相同的拉压子午线附近，由此可以认为，在本文的加载速率范围和加载路径条件下，八面体静动强度包络线与加载方式无关，只与破坏时的应力状态相关.从图5还可以看出，随着应变速率的增加，混凝土的八面体剪切破坏面逐渐向外推移，但是推移的程度并不均衡:静水压力较低时破坏面向外移动明显，静水压力较高时，随应变速率改变而移动的趋势不十分明显；而随着应变率的减小，考虑应变率效应的动态强度准则逐渐逼近于静力强度准则.

3.4 验证双轴动态应力状态

三轴应力空间的破坏准则方程也可以表示为平面应力状态下的双轴强度包络线，见图6、7.图中双轴动态强度均被单轴静态强度正则化.图6中，在相同的应变率下，双轴比例加载和定侧压加载所得的强度数据基本在相同的包络线附近，这里又一次证明了在双轴应力条件下，极限强度包络线与加载路径无关；图6还表明不同侧压下的率效应是不相等的，在较低侧压力水平时强度增强效应更明显.模型计算结果与试验结果非常接近；在图7中，双轴拉压强度分别低于单轴抗拉强度和单轴抗压强度，但随着应变率的提高，各种应力组合下的动态拉压强度均有提高的趋势，这也符合所观察到的试验现象.需要说明的是，图7中使用的是在不同侧压力水平下混凝土立方体试件的静动劈拉强度试验数据，试验难度比较大，试验结果离散性也比较大，致使拉压区有效的动态试验数据比较少，因此该强度准则在拉-压区的双轴强度包络线变化规律有待试验的进一步验证.

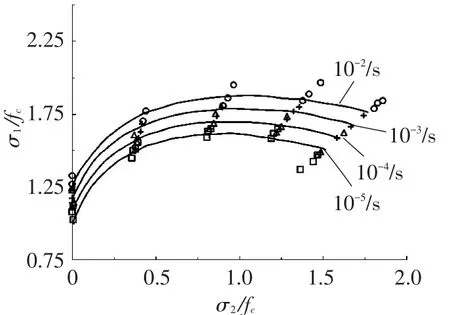
图6 建议破坏准则与不同应变速率下混凝土双轴强度试验数据的比较（压压区）

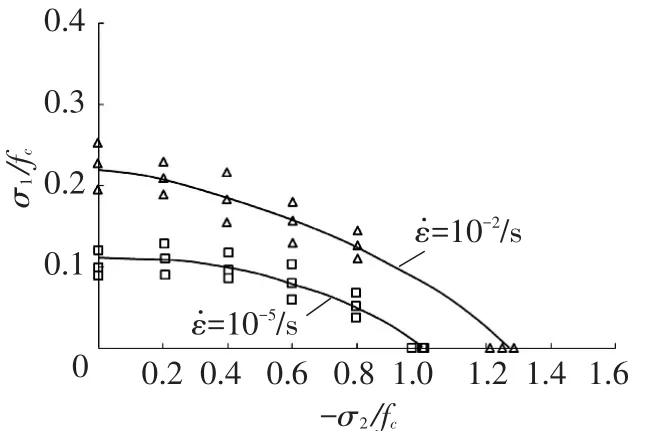
图7 建议破坏准则与不同应变速率下混凝土双轴强度试验数据的比较（拉压区）

4 结 语

本文采用Willam-Warnke模型在偏平面上的椭圆曲线，在八面体应力空间建立了考虑应变率效应的统一多轴静动强度准则，该强度准则符合混凝土破坏曲面的一般特性，满足曲面连续、光滑、外凸等要求，能系统、全面地反映不同混凝土材料的多轴静态和动态强度变化规律，比如，能反映出荷载比例不同时应变速率敏感性不相同的特点.所提出的强度准则，与试验数据吻合度较好，可适用于平面应力或三轴应力状态下中低强度的混凝土.并且，强度准则的具体表达式只需通过几个特征试验点就能得到，形式简单，便于实际应用.

当加载速率增大时，还有很多因素会影响混凝土强度的增加，如湿度和温度等环境因素对混凝土动态强度也会产生一定的影响，本文暂时未考虑这些因素.对于不同湿度和温度下混凝土的动态强度准则，则需要根据实际试验数据重新标定参数.

［1］BISCHOFF P H，PERRY S H.Compressive behavior of concrete athighstrainrates［J］.Materialsand Structures，1991，24（6）:425-450.

［2］MALVAR L J，ROSS C A.Review of strain rate effects for concrete in tension［J］.ACI Materials Journal，1998，95（6）:435-439.

［3］ROSS C A，TEDESCO J W，KUENENNE S T.Effect of strain rate on concrete strength［J］.ACI Journal，1995，92（1）:37-47.

［4］GRAN J K，FLORENCE A L，COLTON J D.Dynamic triaxial tests of high-strength concrete［J］.Journal of Engineering Mechenics，ASCE，1989，115（5）:891-904.

［5］CHEN Zhangfusheng，HU Y，LI Qingbin，et al. Behavior of concrete in water subjected to dynamic triaxialcompression［J］.JournalofEngineering Mechanics，ASCE，2010，136（3）:379-389.

［6］YANDongming，LINGao，CHENG.Dynamic properties of plain concrete in triaxial stress state［J］. ACI Materials Journal，2009，106（1）:89-94.

［7］吕培印.混凝土单轴、双轴动态强度和变形试验研究［D］.大连:大连理工大学，2001.

［8］过镇海.混凝土的强度和变形:试验基础和本构关系［M］.北京:清华大学出版社，1997.

［9］DU Xiuli，LU Dechun，GONG Qiuming，et al.Nonlinear unified strength criterion for concrete under 3-D stress state［J］.Journal of Engineering Mechanics，ASCE，2010，136（1）:51-59.

［10］CHEN W F.Plasticity in reinforced concrete［M］.New York:McGraw-Hill，1982.

［11］宋玉普.多种混凝土材料的本构关系和破坏准则［M］.北京:中国水利电力出版社，2002.

［12］闫东明.混凝土动态力学性能试验与理论研究［D］.大连:大连理工大学，2006.

［13］宋玉普.混凝土的动力本构关系和破坏准则（上册）［M］.北京:科学出版社，2012.

（编辑 赵丽莹）

A dynamic strength criterion of concrete under multiaxial stress state

WANG Huailiang1，2，SONG Yupu3
（1.Civil and Architectural Engineering College，Dalian University，116622 Dalian，Liangning，China；2.State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，430072 Wuhan，China；3.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，116024 Dalian，Liaoning，China）

In order to understand the dynamic strength properties of the concrete under complex stress state，a united multiaxial static-dynamic strength criterion is established in the octahedral stress space in which the strain rate effect is considered.The failure surface of the proposed model in three-dimensional（3D）stresses space is represented by a quadratic function.The strength envelope in the deviatoric plane is described by an elliptic curve similar to that of Willam-Warnke model，and the tensile and compressive meridians are calibrated using typical stress points method to consider the effect of the Lode angle on the dynamic strength. By the analysis of multiaxial static and dynamic strength test data of concrete，it is proved that the predicted strength of the failure criterion is in good agreement with the experimental data.Meanwhile，the strength criterion has simple expression form and is convenient for practical application.

concrete；strain rate；Lode angle；strength criterion；typical stress points

TU375

A

0367-6234（2014）04-0093-05

2013-03-18.

国家自然科学基金资助项目（50908026）；武汉大学水

资源与水电工程科学国家重点实验室开放基金（2012B102）；河海大学水文水资源与水利工程科学国家重点实验室开放基金（2013491811）.

王怀亮（1979—），男，博士，副教授；

宋玉普（1944—），男，教授，博士生导师.

王怀亮，whuailiang＠163.com.