低干缩延性材料-混凝土复合梁抗弯性能

居贤春，张 君，王振波，施正捷

低干缩延性材料-混凝土复合梁抗弯性能

居贤春，张 君，王振波，施正捷

（清华大学土木工程系结构安全与耐久教育部重点实验室，100084北京）

为研究延性材料对普通混凝土的增强增韧效果，本文采用低干缩高延性纤维增强水泥基复合材料（LSECC）与普通混凝土复合的方式，从试验与模拟两个方面研究了复合梁的抗弯性能.结果表明，在梁底复合低干缩延性材料后不仅可以提高梁的抗弯承载能力，还大幅提升了梁的延性.当LSECC的强度比上层混凝土的强度高时，复合梁的峰值荷载受LSECC层厚的影响明显，随着层厚的增加而增大.当上层混凝土的强度较高时，复合梁的峰值荷载随LSECC层厚度的变化不明显.基于开裂强度和材料应力裂纹宽度关系的抗弯模型可良好地预测不同材料复合梁的弯曲性能，模型结果与实测值吻合良好，可用于组合结构优化设计.

低收缩延性纤维增强水泥基复合材料（LSECC）；混凝土；复合梁；抗弯性能

混凝土结构在环境与机械荷载联合作用下开裂通常是由表面开始的，因此混凝土构件表层防裂对提高耐久性尤为重要［1］.同时，近年研究开发的高延性聚乙烯醇纤维增强水泥基复合材料（PVA-ECC）价格仍然偏高［2］，这也限制了它在结构中的应用.鉴于以上两点原因，为了提高性价比，延性材料与普通混凝土的组合模式是一个很好的节约成本、发挥各自优势的好方式，即采用延性材料作为普通混凝土结构的防护面层，而结构主体部分仍沿用普通混凝土［3-6］.此外具有低收缩特性的基材克服了传统ECC材料和普通混凝土协同工作的问题，使其因变形不协调而容易出现界面破坏的概率降低［2］，所以这种组合模式在未来混凝土结构面层抗裂，进而提高结构耐久性、延长其服役寿命方面具有良好的发展前景.

作为混凝土结构面层抗裂应用的初步研究，本文开展了低干缩高延性纤维增强水泥基复合材料（LSECC）与普通混凝土复合梁的抗弯性能试验研究与理论模拟，即在梁的受拉区用延性良好的LSECC材料，受压区仍旧用普通混凝土.试验中采用两个强度等级的普通混凝土，C30和C80混凝土，两个强度等级的LSECC进行组合；同时变化LSECC层的厚度，研究这些参数变化对复合梁抗弯性能的影响.最后基于已有的混凝土与LSECC材料的抗拉本构关系，即拉压应力-应变关系和桥接应力-裂纹宽度关系，建立了LSECC-混凝土复合梁的抗弯性能计算预测模型，并分析了主要参数的影响，为未来基于LSECC材料防护的高性能、高耐久混凝土结构设计提供试验与理论支撑.

1 试验方法

LSECC-混凝土复合梁采用热接模式，即混凝土与LSECC材料先后在水泥凝结硬化前浇筑完成.其成型过程为:首先浇筑LSECC部分，采用100 mm×100 mm×400 mm的钢制模具，按预设厚度，先浇注底部LSECC材料，2 h左右（水泥终凝前）再浇注上部混凝土，整个模具填满并振捣密实.为防止水分蒸发，试件表面采用塑料膜覆盖.成型24 h后拆模，试件放标准养护室（温度20±3℃，湿度＞90%）养护至7d进行三点抗弯试验.成型后的复合梁示意见图1，其中混凝土层和LSECC层厚度按要求设计浇筑.复合梁抗弯试验在TONINORM2000试验机上完成，试件尺寸100 mm×100 mm× 400 mm，支点间距350 mm，采用线性变形传感器测定跨中挠度，并以此控制加荷速度，即0.1 mm／min，荷载、变形数据自动采集，分率为20次／s.

图1 热接复合梁示意（mm）

试验用聚乙烯醇纤维参数与力学性能列于表1.复合梁受拉区采用表2所示的两个不同强度等级的的LSECC，其中增强纤维掺量为体积含量2.0%.两种LSECC材料抗拉、抗压等力学性能参数也列于表中，其中抗压试块尺寸为70.7 mm× 70.7 mm×70.7 mm.混凝土部分采用C30和C80两个强度等级的普通混凝土，配合比与28 d标准养护时抗压强度如表3所示，其中抗压试块尺寸为100 mm×100 mm×100 mm.LSECC和普通混凝土的层厚分别选用0／100、30／70、50／50、70／30、100／0进行成型.

表1 试验用聚乙烯醇（PVA）纤维的相关材料性能

表2 复合梁用LSECC配合比及力学性能参数

表3 复合梁用普通混凝土配合比及力学性能参数

2 试验结果

三点抗弯试验获得的不同强度、不同厚度复合梁的荷载-挠度关系曲线见图2～3.

复合梁受弯后，在底部LSECC层出现多条微细裂缝，裂缝延伸至普通混凝土层后在混凝土层内形成一条主裂缝，复合梁受弯后典型开裂模式见图4.

图2 低强度等级LSECC与混凝土组合后荷载-挠度曲线

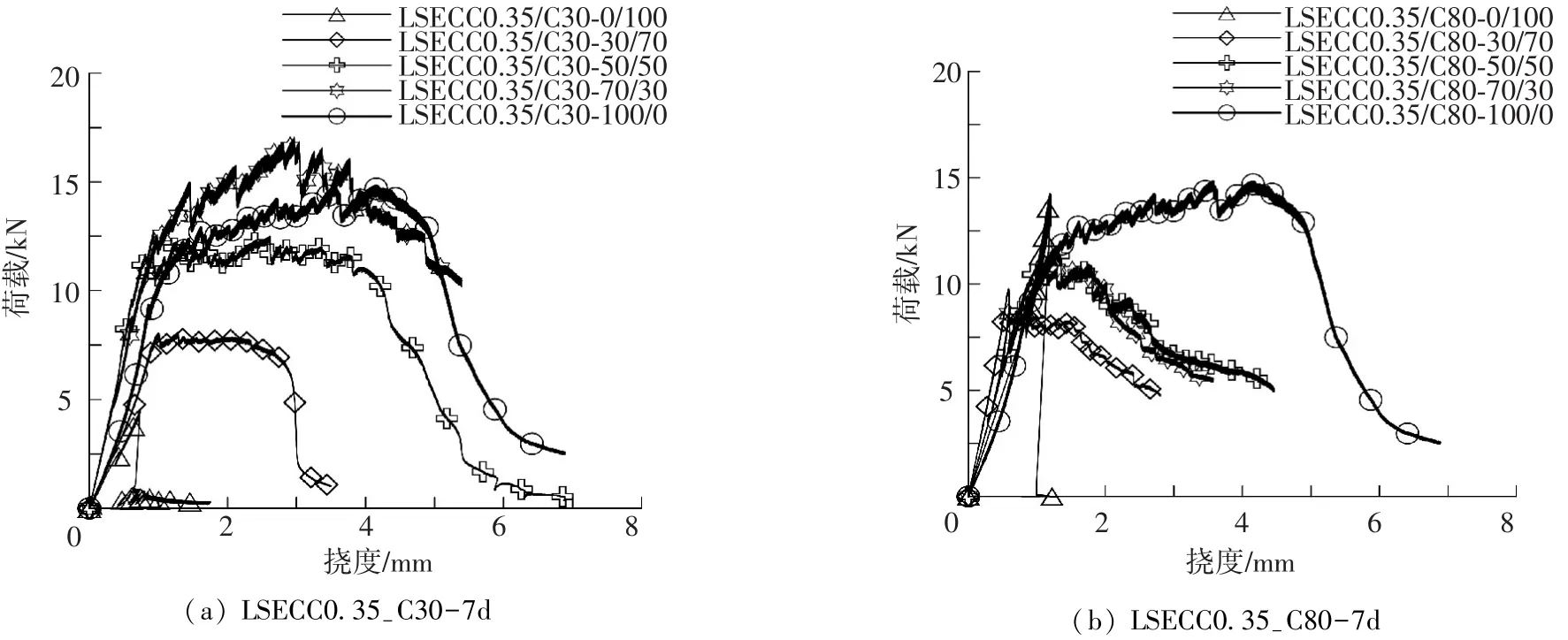
图3 高强度等级LSECC与混凝土组合后荷载-挠度曲线

图4 典型的复合梁抗弯开裂模式

从图2～3所示的抗弯试验结果，首先可以看出，没有LSECC层的普通混凝土梁开裂后裂纹迅速扩展直至断裂，弯曲荷载下梁呈现明显的脆性破坏特征，承载力达极限时梁的跨中挠度（临界挠度）仅为0.9～1 mm.如预期，C80混凝土的抗弯荷载明显高于C30混凝土的抗弯荷载.其次，底部有LSECC层的复合梁开裂后先在LSECC层内出现多条细密裂纹，随着荷载的增加，裂纹持续扩展并增多.裂纹延伸至普通混凝土层后向混凝土内延伸，并形成单一的裂缝，裂纹随荷载增加扩展接近梁顶时，复合梁仍能够承受荷载，随着跨中挠度的增大，裂纹宽度持续增加，荷载缓慢下降，复合梁呈现明显的延性破坏特征，临界挠度明显增大，破坏时跨中挠度大都在3 mm以上.第三，对C30混凝土，与LSECC复合后梁的抗弯承载力获得明显提高，延性层材料强度越高，复合梁抗弯强度提高越明显.对C80混凝土，当采用强度低的延性层与之组合时，复合梁的抗弯强度低于C80素混凝土梁，当采用强度较高的延性材料与之复合时，复合梁的抗弯强度与单一素混凝土梁相当.第四，随着LSECC层厚度增大，复合梁的延性提高，临界挠度增大.同时LSECC层厚度对复合梁的强度也有正面影响.各类复合梁的抗弯强度与临界挠度随LSECC层厚度变化见图5、6.

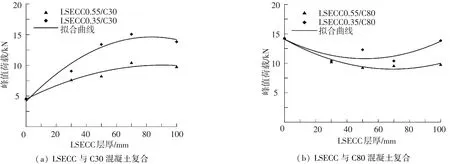
图5 LSECC-混凝土复合梁的峰值荷载随LSECC层厚的变化关系

图6 LSECC-混凝土复合梁的临界挠度随LSECC层厚的变化关系

3 理论模拟

为了将延性材料与混凝土的组合结构更好地应用于实际工程，希望建立基于材料本构关系的复合材料性能预测模型，进而为未来带有防护面层的混凝土结构设计提供帮助.下面以LSECC-混凝土双层复合梁为例，建立其抗弯性能预测模型，并与实验结果对比.建模之前做如下假设:（1）LSECC和普通混凝土在界面处应变协调，不发生错动；（2）弯曲荷载下主裂纹裂缝（控制弯曲荷载大小）从梁底正中垂直向上延伸.

设混凝土梁受三点弯曲荷载作用，基于开裂强度准则，当梁底部跨中水平方向拉应力达到材料开裂强度时，弯曲裂纹形成并开始向上扩展.缝间由于骨料、水泥颗粒及增强纤维的作用，其裂纹表面作用有使裂纹闭合的桥接应力，通常称之为缝间粘聚力，该裂纹称之为粘性裂纹.粘聚裂纹尖端的主拉应力等于材料的开裂强度σfc，对应裂纹张开位移为零.桥接应力的大小与裂纹宽度相关［7-8］，由桥接应力-裂纹宽度关系来描述.材料的桥接应力-裂纹宽度关系是材料抗拉属性.为便于计算，将应力与裂纹宽度间关系模拟为多段线性函数，即:

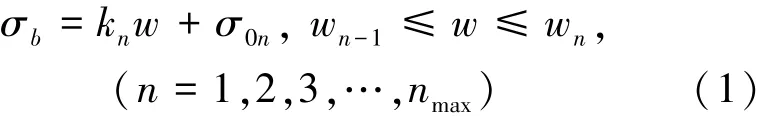
式中:kn、σ0n分别为第n段线段的斜率和截距，可由材料的桥接应力-裂纹宽度关系确定；nmax为线段数，通常取决于应力-裂纹宽度关系的弯曲程度．

下面推导复合梁在弯曲荷载下内外力之间的平衡关系．图7为典型的三点抗弯梁，假设开裂后跨中粘性裂缝长度为a，平衡时外荷载为P，此时作用于裂纹表面的粘聚力为σb（w（x）），为x处裂纹张开宽度的函数．根据叠加原理，在裂纹上任意点的张开位移w（x）可表达为［9］

此时裂纹尖端的应力可表达为

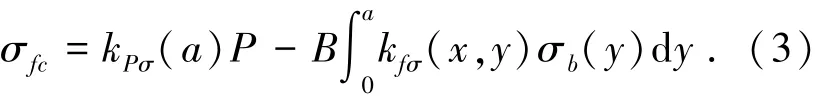
式中:kPw，kfw和kPσ，kfσ分别为外载和粘聚力对裂纹表面x处裂纹张开宽度和裂纹尖端应力的影响因子，B为梁宽．通过对上述方程进行离散化数值求解，就可获得给定裂纹长度（a）和材料性质（材料的应力-裂纹宽度关系）时复合梁承载力（P）和相应的裂纹张开宽度w（x）．

图7 开裂混凝土梁在弯曲荷载及粘聚力作用下的叠加原理

将裂纹间的桥接应力离散成如图8所示的节点力，其中节点沿着裂纹竖直分布，节点力的大小由材料的应力-裂纹宽度关系（σ-w）确定．方程（2）、（3）的离散化形式分别为

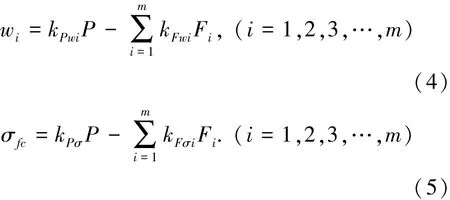
由式（1），Fi与wi可以建立如下联系:

Fi=（knwi+σoi）BΔli．（i=1，2，3，…，n）（6）式中Δli是位于节点i处的计算长度．除i=1时，Δli=0.5Δl外，其他均有Δli=Δl，Δl为两个相邻节点间距．以上3个方程式构成2m+1个方程组，含有2m+1个未知数，即x≡（P，w1，w2，w3，…，wm，F1，F2，F3，…，Fm），通过求解便可获得给定裂纹长度a时，各节点处裂纹张开宽度wi、相应粘聚力Fi和抗弯承载力P．下面讨论影响因子的求解与需要输入的材料应力-裂纹宽度关系．

影响因子的求解:首先采用有限元构建三点弯曲试验梁模型.梁的长、宽、高分别为400 mm，100 mm和100 mm，支点间距350 mm.由于梁的几何及受力对称，因此需构建半根梁的有限元模型进行相应参数求解，本文取有限元网格间距为2.5 mm.对于每一种层厚和上下层不同材料的组合，需分别建立模型，赋予相应的材料参数（弹性模量）和层厚.在跨中未开裂部分，在每个节点处设定一个横向支座，模拟没有横向位移而只有竖向位移的特性，裂纹扩展开裂过程通过至下而上地释放这些横向支座来模拟.这样，对给定裂纹长度，缝间粘聚力离散为裂纹表面的节点力Fi（如图8所示），相应裂纹张开宽度为wi．所谓某一外力的影响因子（外力依据裂纹长度大小，有P，F1，…，Fm），就是在该力的作用点上施加相同方向的单位力，并将其他节点处的外力设置为零，然后通过有限元计算，求得该节点的单位力对裂纹尖端应力、裂纹表面各节点张开宽度的结果．例如，当裂纹长度a=5 mm时，外载P对第1个开裂节点的横向位移w1的影响因子的求解过程为:（1）释放跨中由下向上的2个横向支座，模拟开裂长度为5 mm；（2）在模型的跨中节点施加竖直向下、大小为1 kN的单位力；（3）运行有限元程序对模型进行计算；（4）找出节点1的横向位移w1P，则w1P就是P对于w1的影响因子kPw1．在此计算中同样可以获得P对第二个节点张开宽度w2的影响因子kPw2．同时，通过读取裂纹尖端节点的水平方向拉应力值，就可获得此裂纹长度时外力P对裂纹尖端水平拉应力的影响因子kPσ．以此办法，即可获得式（4）、（5）中与裂纹长度相对应的所有影响因子，形成方程组的系数矩阵．另外有限元计算中单元大小对计算结果有一定影响，本文通过大量尝试，跨中开裂区节点间距取1.5～2.5 mm时计算结果差异很小，为此计算中统一取节点间距2.5 mm．

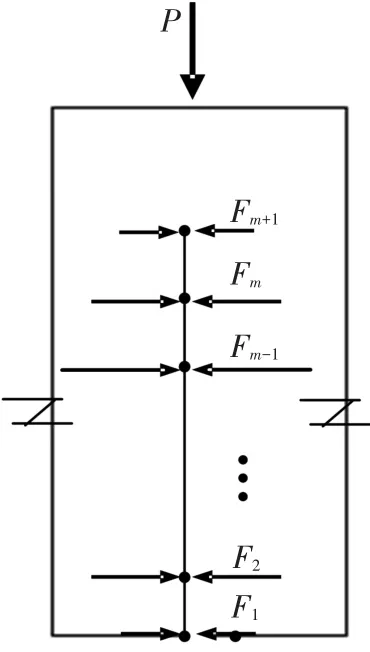
图8 离散化桥接应力分布示意

方程中需要的各材料的应力-裂纹宽度关系，本文借助文献［8，10］中得到的C30，C80及两个强度等级的LSECC材料的桥接应力与裂纹宽度的关系，对上述方程进行了求解.图9分别为4种材料的σ-w关系图，然后按模型（1）进行多段线性关系模拟，获得相应参数.

图9 两种材料的应力-裂纹宽度关系

4 模型结果及分析

选取了4种材料厚度组合（延性材料／混凝土为0／100、30／70、50／50、0／100）和4种强度组合（LSECC0.55／C30、LSECC0.55／C80、LSECC0.35／C30、 LSECC0.35／C80），通过上述方法计算得到7 d龄期时复合梁荷载的抗弯性能.图10、11所示为计算获得的不同复合梁的弯曲荷载-裂纹口张开宽度（CMOD）关系曲线.

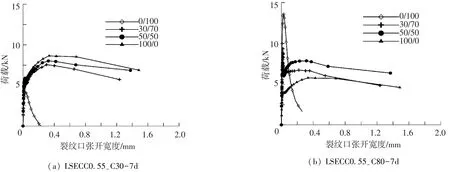
图10 低强度LSECC材料与混凝土复合梁荷载-裂纹宽度关系

图11 高强度LSECC材料与混凝土复合梁荷载-裂纹宽度关系

从计算结果可得到和实验结果类似的结论，没有延性材料层的普通混凝土梁开裂后裂纹迅速扩展直至断裂，呈现明显脆性断裂特征，与峰值荷载相对应的仅为0.05 mm左右.底部有LSECC层的复合梁底部开裂后呈现应变硬化特点（承载力随裂纹宽度增加而增大），荷载达到峰值荷载后缓慢下降，呈现明显的延性破坏特征.与峰值荷载相对应的裂纹张开宽度达到0.4～0.8 mm，较素混凝土大幅度增加.延性材料层厚度增加，延性改善越明显.此外，延性材料与普通混凝土的强度匹配对复合梁抗弯性能影响明显，在保证延性前提下采用更高强度的延性材料更有利于提高复合梁延性的同时，提高其承载能力.

图12 LSECC-混凝土复合梁抗弯承载力模型计算与实测结果比较

模型计算得到的承载力与实验测得的结果对比见图12，图中实线为模型计算结果，数据点为实验测得的结果.模型计算结果与实验结果总体趋势吻合良好，模型预测的承载力随延性材料层厚变化趋势与试验结果相同，表明基于开裂强度和材料应力裂纹宽度关系的抗弯模型可良好地预测复合梁的弯曲性能.模型结果与实验结果的个别值有一定差异，例如高强度延性材料与高强混凝土复合的部分结果的试验值较计算值偏低，除了材料有一定的性能离散性外，还可能与模型假设的两材料界面完全无剪切滑移有关，不同材料层界面可能的剪切滑移会影响模型结果，这些将在未来研究中加以考虑.

5 结 论

1）在梁底复合延性材料后不仅可以提高梁的抗弯承载能力，还大幅提升了梁的延性.当LSECC的强度比上层混凝土的强度高时，复合梁的峰值荷载受LSECC层厚的影响明显，随着层厚的增加而增大.当上层混凝土的强度较高时，复合梁的峰值荷载随LSECC层厚度的变化不明显.

2）基于开裂强度和材料应力裂纹宽度关系的抗弯模型可良好地预测不同材料复合梁的弯曲性能，模型结果与实测值吻合良好，可用于组合结构优化设计.

［1］梁立农.混凝土桥梁耐久性的若干问题［J］.广东公路交通，2002，76（增刊1）:45-51.

［2］ZHANG Jun，GONG Chengxu，ZHANG Minghua，et al. Engineered cementitious composite with characteristic of low dryingshrinkage［J］.CementandConcrete Research，2009，39（4）:303-312.

［3］QIAN Shunzhi，LI V C，ZHANG H，et al.Life cycle analysis of pavement overlays made with engineered cementitious composites［J］.Cement and Concrete Composites，2013，35（1）:78-88.

［4］ZHANG Jun，LI V C，NOWAK N S，et al.Introducing ductile strip for durability enhancement of concrete slabs［J］.ASCE Journal of Materials in Civil Engineering，2002，14（3）:253-261.

［5］ZHANG Jun，LI V C.Monotonic and fatigue performance of engineered fiber reinforced cementitious composite in overlay system［J］.Cement and Concrete Research，2002，32（3）:415-423.

［6］LEUNG C K Y，CHEUNG Y N，ZHANG Jun.Fatigue enhancement of concrete beam with ECC layer［J］. Cement and Concrete Research，2007，37（5）:734-750.

［7］李启宏，张君，赵金平.纤维增强水泥薄板及其复合梁的抗弯性能研究［J］.工程力学，2011，28（5）: 135-142.

［8］张君，王林，刘骞.粗细骨料比例和水泥石强度对混凝土断裂参数的影响［J］.工程力学，2003，21（1）: 136-142.

［9］COX B N，MARSHALL D B.Stable and unstable solutions for bridged cracks in various specimens［J］. Acta Metall.Mater.，1991，39（4）:579-589.

［10］ZHANG Jun，JU Xianchun.Investigation on stresscrack opening relationship of engineered cementitious composites using inverse approach［J］.Cement and Concrete Research，2011，41（8）:903-912.

（编辑 赵丽莹）

Flexural performance of LSECC-concrete composite beam

JU Xianchun，ZHANG Jun，WANG Zhenbo，SHI Zhengjie
（Dept.of Civil Engineering，Key Laboratory of Structural Safty and Durability of China Education Ministry，Tsinghua University，100084 Beijing，China）

To investigate the effect of ductile material on strength and ductility improvement of concrete，the flexural performance of LSECC-Concrete composite beam，in which the ductile fiber reinforced cementitious composite with characteristic of low shrinkage（LSECC）was used at the tensile part of the beam，was studied by both experiments and theoretical simulation.The results show that the concrete beam combined with ductility material at the bottom of beam can achieve a high ductility and enhance load carrying capacity.The strength of the LSECC and plain concrete，as well as the thickness of LSECC layer used in the composite beams can greatly influence the strength and ductility of the beam.Based on cracking strength criteria and stress-crack opening relationship，a model to simulate bending performance of composite beam is developed，which can well predict the flexural behavior of composite beam.A seasonable agreement between model and test results is observed and the model may be used in optimization of the composite structures.

low shrinkage engineered cementitious composites（LSECC）；concrete；composite beam；flexure

TU528

A

0367-6234（2014）04-0075-07

2013-06-27.

国家科技支撑计划资助项目（2011BAJ09B01）；国家自

然科学基金资助项目（51278278）.

居贤春（1985—），男，博士研究生；

张 君（1962—），男，教授，博士生导师.

张 君，junz＠tsinghua.edu.cn.