基于雅可比旋量统计法的发动机三维公差分析

陈华，唐广辉，陈志强，李志敏，金隼

（1.上海交通大学上海市复杂薄板结构数字化制造重点实验室，上海200240；2.上汽通用五菱汽车股份有限公司，广西柳州545007）

基于雅可比旋量统计法的发动机三维公差分析

陈华1，唐广辉2，陈志强2，李志敏1，金隼1

（1.上海交通大学上海市复杂薄板结构数字化制造重点实验室，上海200240；2.上汽通用五菱汽车股份有限公司，广西柳州545007）

为了在发动机装配体的公差分析中考虑传统尺寸链无法处理的几何公差信息，以发动机的做功机构为分析对象，引入雅可比旋量模型，建立在尺寸和形位公差约束下的特征及其配合旋量的变动和约束方程。将其融入到蒙特卡洛算法中，实现发动机做功机构的三维统计公差分析。与传统分析方法相比，基于雅克比旋量模型的分析方法考虑了更多的几何公差信息，分析结果也更加精确，该模型可以从尺寸链角度建立发动机零部件公差与整机性能的映射关系。

雅可比旋量；统计法；三维公差分析；做功机构；发动机

对于发动机而言，燃油消耗率、功率、扭矩等性能指标是汽车顾客最为关心的问题。研究表明，单缸燃烧室压缩比的波动及其缸间的差异化是影响油耗的一个重要因素，零部件之间的运动摩擦功耗对整机输出功率有较大影响，这些都与零部件的公差设计和累积直接相关。零部件公差与整机性能的映射关系是发动机领域一个亟待解决的问题。

发动机的做功机构，包括曲轴及轴瓦、连杆及连杆瓦、活塞销和活塞、以及作为支撑件的气缸体，是发动机最为重要的功能组件之一，也是压缩比的重要构件和摩擦功的主要制造者。以某型四缸汽油机为例，做功机构的累积公差可导致压缩比波动6%，仅次于缸盖燃烧室和活塞燃烧室的容积公差导致的波动。同时，该机构的摩擦功占整机摩擦功的70%以上［1］。

目前，该机构的公差设计以经验为主，公差分析和分配基于传统的平面尺寸链和极值法，分析对象仅限于零部件的尺寸公差。对于图纸上大量的几何公差信息，一直缺乏标注依据和分析手段。

三维公差分析技术在空间领域描述特征在公差域的微小变动，以及这些变动矢量在装配链中的传递关系，能有效的表达和传递除尺寸公差外的其他几何公差。目前，基于三维几何的公差分析模型主要有：以点集形式包含了满足公差要求的所有公差域边界及变动要素的T-Map模型［2］；用齐次变换矩阵表示实际特征在公差域中变动的矩阵模型［3］；将包含装配偏差和几何偏差的非线性隐式装配关系一阶线性展开的直接线性法（direct linearization method，DLM）模型［4，5］；视公差域为虚拟关节运动空间，用雅可比矩阵计算各关节与末端之间的公差传递的雅可比模型［6］；基于工艺拓扑相关表面理论，适合公差表示的小位移旋量（small displacement torsor，SDT）模型［7］；以及结合了雅可比和小位移旋量模型的雅可比旋量模型［8］等。其中，雅可比旋量模型算法简洁，工程语义丰富，特别适合于以圆柱和平面特征为主的复杂装配体三维公差建模，除极值算法外，还能实现统计算法。

将三维公差分析技术与统计算法结合起来是当前的研究热点［9］。本文引入雅可比旋量模型，以发动机做功机构为分析对象，建立在尺寸和形位公差约束下的特征及其配合旋量的变动和约束方程，将其融入到蒙特卡洛算法中，实现发动机做功机构的三维统计公差分析，并详细分析计算结果。

1 雅可比旋量统计算法

1.1 雅可比旋量模型

雅可比旋量模型结合了2个重要的概念，即适合公差传递的雅可比矩阵和适合公差表示的旋量模型。

在公差分析中，可将各公差域所蕴含的变动视为虚拟关节的运动，用雅可比矩阵将其传递到装配尺寸链的封闭环。为方便分析计算，这里将公差分为两类，即功能要求副（functional requirement，FR）和功能单元副（functional element，FE）。FR为设计目标值，通常为封闭环；FE根据是否属于同一个零件又可以分为内部功能单元副（internal FE，IFE）和接触功能单元副（contact FE，CFE）。雅可比矩阵用于公差分析的传递模型可表达为

式中：δS和δα分别代表FR的3个平动矢量和3个转动矢量；δq[]FEi代表各FE中的小位移矢量；n为FE的数目；J[]FEi为各关节对应的雅可比矩阵，其数学表达式为

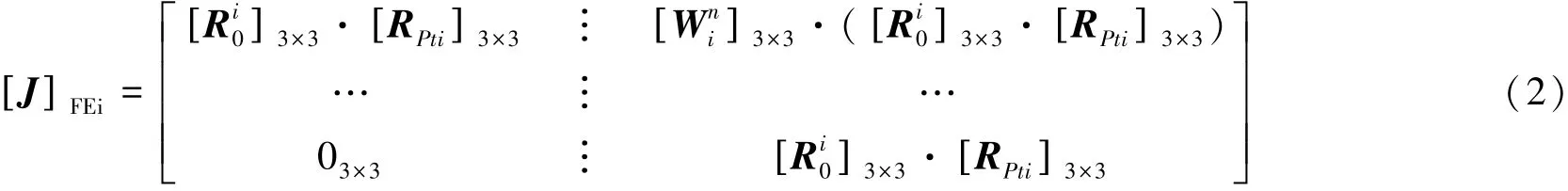
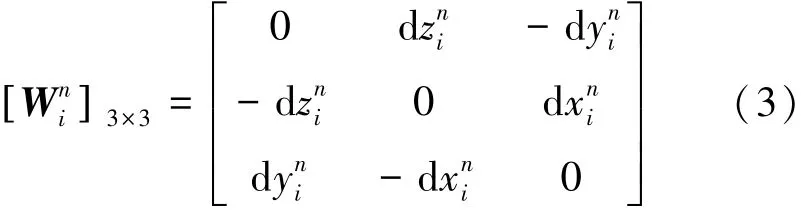
旋量法是螺旋理论在公差领域的具体应用，因其分析对象为小位移转动或平动，故也称小位移旋量。如图1所示，公差域可视为实际特征S1对理想特征S0的变动空间，由3个沿坐标轴平动的矢量和3个绕坐标轴转动的矢量组成。S1相对于S0的小位移旋量可表示为

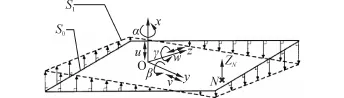
图1 面特征的旋量表示模型Fig.1 Screw model of a planar feature

对于S0上的任一点N，S1的变动空间，即公差域的旋量表示为

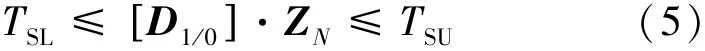
式中：ZN为N点的法向量，TSU为上公差，TSL为下公差。

小位移旋量模型用运动旋量来表示公差变动域，有严格的数学定义及丰富的工程语义。但对于公差的传递和累积，却不如雅可比矩阵方便直接［10］。

综合雅可比矩阵和小位移旋量模型，就是雅可比旋量模型，其表达式为

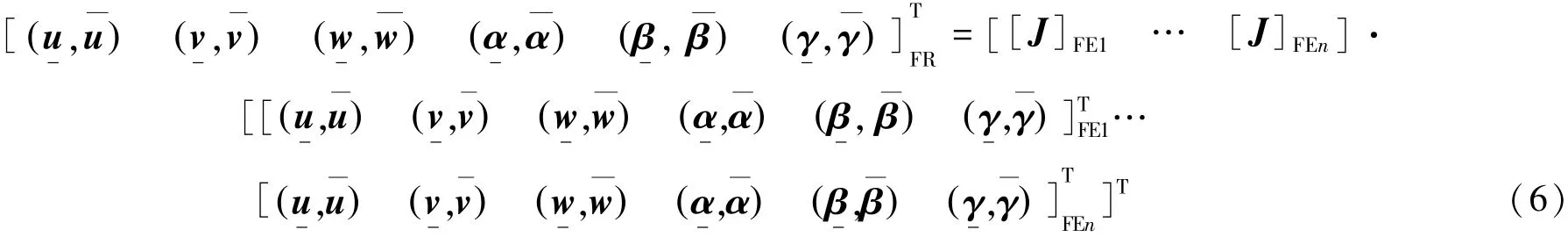
从式（6）可以看出，基于雅可比旋量模型的公差分析方法具有简洁的数学表达式、可量化位置和方向公差、丰富的工程语义等特点。然而，对于雅可比旋量模型，极值法的求解与公差标准相矛盾，因为同一FE的各矢量之间存在约束关系，而非彼此独立。基于蒙特卡洛算法的统计法能在计算过程中考虑这种约束关系，因而可将统计法引入到雅可比旋量模型中，这就是雅可比旋量统计算法。

1.2 雅可比旋量统计算法

众所周知，零件的加工质量都呈现出一定的统计规律，其分布特征取决于工序能力和工艺技术。统计法也意味着一定的废品率和不完全互换性，但相比于极值法，统计法更符合生产实际，且对组成环的公差分配较为宽松。

Ghie等［11］提出了雅可比旋量模型的统计算法，但在计算过程中忽略了属于同一旋量的矢量之间的约束关系。本文提出了一种新的算法，能将旋量的变动和约束关系融入到计算流程中，使得计算结果更加合理。其流程如图2所示。其中，i为实际仿真次数，N为设定仿真次数。

图2 雅克比旋量模型统计法计算流程Fig.2 A statistical scheme for the Jacobian-Torsor model

该算法基于蒙特卡洛模拟方法，关键在于建立特征的变动和约束方程，并将其应用到蒙特卡洛算法中。对于不同的特征和公差类型，以及特征之间的配合，都对应不同的变动和约束方程［12-13］。

发动机做功机构的各零部件以圆柱和平面特征为主，装配约束主要是面匹配和轴孔间隙配合。在各种公差约束下，建立平面和圆柱特征，及其配合的变动和约束方程，然后代入到雅可比旋量统计算法流程中，就可对做功机构进行三维统计公差求解。

2 做功机构三维统计公差分析

图3所示为某型发动机第三缸活塞处于上止点时的功能要求示意图，FR对发动机的压缩比有直接的影响。

图3 功能要求图Fig.3 Functional requirement

图4 为与FR相关的各零件设计公差图。为方便计算，本文将曲轴瓦与曲轴孔视为一体，称为缸体组件；将连杆大端孔与连杆瓦视为一体，称为连杆组件。计算过程由基于Matlab编制的程序完成，其步骤如下：

1）建立雅可比旋量模型。做功机构的装配尺寸链传递见图5所示，坐标系固结于各零件公差域的中间位置，坐标及方向如图4所示，各坐标方向均相同以避免投影换算。该装配体包含两条串联环路：IFE1-IFE9-FR和CFE2-IFE3-CFE4-IFE5-CFE6-FE7-IFE8-FR，故需建立2个雅可比旋量模型。在本案例中忽略了曲轴和连杆的轴向止推约束，以及缸孔与活塞的圆周约束，以避免产生局部并联而导致无法建立雅可比传递矩阵。

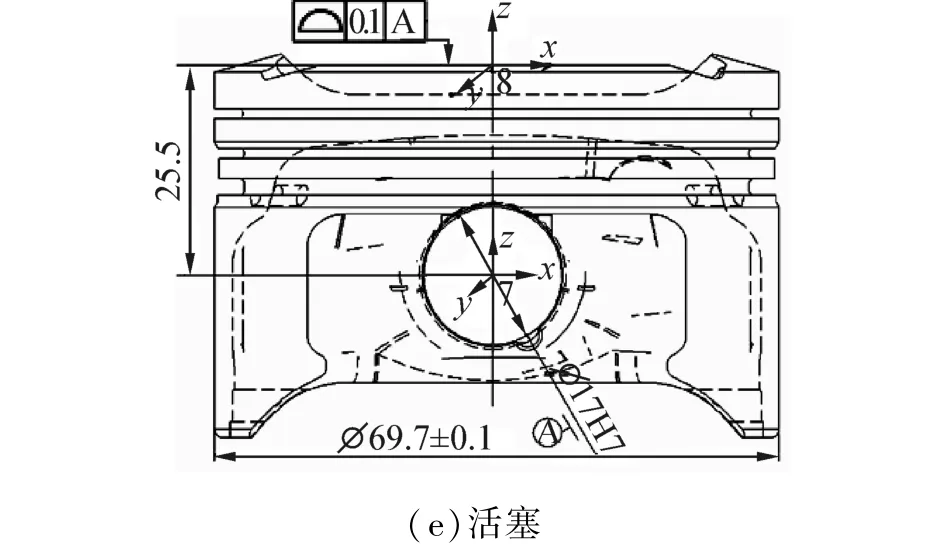
图4 各零件的设计要求图Fig.4 Detailed drawing of each part

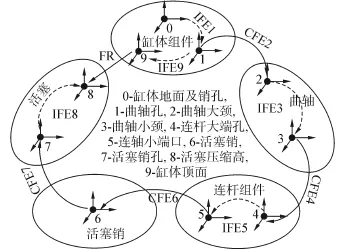
图5 功机构的装配链Fig.5 Connection graph of the working mechanism

由式（2）、（3）可得做功机构的雅可比传递矩阵：

式中：dz1＝dz2＝186，dz3＝dz4＝146.5，dz5＝dz6＝dz7＝25.5，dy1＝dy2＝38，其余未说明向量为零。

2）建立旋量的变动范围和约束。这里给出具有代表性的IFE3和IFE9为例说明。在IFE3中曲轴小颈对大颈有位置度TPO（Φ0.1）和平行度TPAR（Φ0.05））要求，其旋量中各矢量的变动范围为

约束条件为

IFE9为缸体顶面对曲轴孔的位置TPO（Φ0.1）约束，其变动范围为

约束条件为

通常，位置公差限制旋量的平动，而方向公差限制其转动。

平面之间的匹配，一般情况下都默认为完全贴合，故小位移旋量都为零。而圆柱的情况则不同，因为有间隙配合的情况，例如曲轴与曲轴孔的配合，其旋量的变动和约束方程与位置度相同，这里的“位置度”等于轴孔配合的最大间隙值。

3）计算各旋量中矢量的均值和标准差，按概率分布产生随机数。其均值和标准差可由式（12）、（13）得到，其中K为标准化正态数，可依据预定废品率查表得知；μT为变动范围的中值：

这里假设各零部件的废品率都为0.27%，且各矢量都为正态分布，故K＝3，随机数由Matlab中的randn（）函数生成。

4）蒙特卡洛仿真计算。计算由程序实现，需要注意的是仿真次数越多，结果越精确，但也越耗时，这里设置为10 000次。

5）建立FR的直方图，并计算其均值和标准差。对于发动机做功机构，只关注FR在活塞行程方向的公差累积，对应于FR中的w。在程序中建立w的直方图，并计算出均值和标准差。计算结果为：σFR1w＝0.031 1，σFR2w＝0.017 6。二者的均值都非常小，可置为0。

6）结果计算。活塞压缩高至缸体上表面的公差累积为两条公差传递环路之和。在统计法中，FR的标准差为FR1和FR2标准差的平方和的根。上一步计算出FR的标准差，从而得到其公差范围为

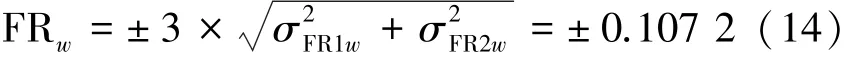
即活塞处于上止点时，活塞压缩高到缸体顶面在z轴方向的累积公差为±0.107 2。

3 结果分析

对于该做功机构，仅考虑尺寸公差的传统平面尺寸链统计算法结果为±0.128 9。对比可以看出，本文提出的基于雅可比旋量模型的统计算法在计算过程中考虑了平行度公差的约束，以及旋量中平动和转动矢量间的约束，从而更加符合公差标准且精度更高，同时也为各组成零部件提供了更为宽松的公差设计空间。

对于做功机构，不仅要知道零部件之间的公差累积，还需要知道各个公差对累积公差的贡献度，为公差优化提供依据。对于雅可比旋量的统计算法，其公差贡献度的计算公式为

经计算并归一化处理，可得到各FE的贡献度排列图，如图6所示。

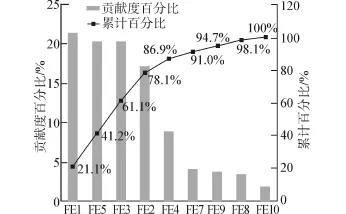
图6 公差贡献度排列图Fig.6 The pareto diagram of tolerance contribution

由图6可以看出，曲轴孔的位置度对做功机构的公差累积影响最为显著，达到21.12%。这也体现了雅可比旋量模型的杠杆效应。图7所示为曲轴孔位置度（Φt）对缸体理论顶面（b）的影响示意图，曲轴中心线在位置度范围内的转动（a′）可导致顶面（b′）超出平动的变动范围（±t／2），且距离d越大，杠杆效应越明显。故曲轴孔的位置度控制越严格越好。

图7 曲轴孔位置度对顶面变动影响示意图Fig.7 Graph for variational top plane influenced by the positional tolerance of hole of crankshaft

曲轴孔位置度、曲轴与曲轴孔的间隙配合、曲轴小径对大颈的位置度、以及连杆小端孔对大端孔的位置度对FR的偏差贡献度之和占总贡献度的78.1%，而剩余的5项只占22.9%，因此，可严格控制前4项，而适当放松后5项，做到质量成本的优化。

值得注意的是，以上流程都是假设零件的加工质量和累积结果符合正态分布，但实际情况中可能还存在其他分布形式，这就需要对测量数据采样分析。对于非正态分布的参数，尤其是计算结果，需分布检验程序。对分布的描述，除了均值和标准差，还应该有偏度和峰度等参数［14］。另外，还可继续分解式（15）以分别求出其中位置和方向公差的贡献度，这里不做展开。

4 结束语

要理清诸如发动机等结构复杂、制造成本相对较高的精密机构零部件公差与性能映射关系，三维公差分析方法可从尺寸链角度提供思路和线索。雅可比旋量统计公差分析方法具有简洁的数学表达式、可量化几何公差信息、准确的计算结果和丰富的工程语义等特点，尤其适合此类机构的公差分析和优化。此外，通过修正雅可比矩阵，实际工况下的热、载荷等影响因素也可以考虑进来［15］，在一定程度上可以减少物理实验，降低开发成本。

［1］钟明明.发动机制造精度与性能关系研究［D］.上海：上海交通大学，2012：6-26.ZHONG Mingming.Research on correlation between manufacturing precision and performance of engine［D］.Shanghai：Shanghai Jiao Tong University，2012：6-26.

［2］AMETA G，SERGE S，GIORDANO M.Comparison of spatial math models for tolerance analysis：tolerance-maps，deviation domain，and TTRS［J］.ASME Journal of Computing and Information Science in Engineering，2011，11：021004-1-8.

［3］WHITNEY D E，GILBERT O L，JASTRZEBSKI M.Representation of geometric variations using matrix transforms for statistical tolerance analysis in assemblies［J］.Research in Engineering Design，1994，6（4）：191-210.

［4］CHASE K W，MAGLEBY S P，GAO J.Tolerance analysis of 2-D and 3-D mechanical assemblies with small kinematic adjustments［C］／／Advanced Tolerancing Techniques.New York：John Wiley＆Sons，1997：103-137.

［5］CHASE K W，GAO J，MAGLEBY S P，et al.Including geometric feature variations in tolerance analysis of mechanical assembly［J］.IIE Transactions，1996，28（10）：795-807.

［6］LAPERRIÈRE L，EIMAREGHY H A.Tolerance analysis and synthesis using Jacobian transforms［J］.CIRP Annals－Manufacturing Technology，2000，49（1）：359-362.

［7］TEISSANDIER D，COUÉTARD Y，GÉRARD A.A computer aided tolerancing model：proportioned assembly clearance volume［J］.Computer-Aided Design，1999，31：805-817.

［8］DESROCHERS A，GHIE W，LAPERRIÈRE L.Application of a unified Jacobian-Torsor model for tolerance analysis［J］.ASME Journal of Computing and Information Science in Engineering，2003，3：1-13.

［9］HONG Y S，CHANG T C.A comprehensive review of tolerancing research［J］.International Journal of Production Research，2002，40（11）：2425-2459.

［10］MARZIALE M，POLINI W.A review of two models for tolerance analysis of an assembly：Jacobian and Torsor［J］.International Journal of Computer Integrated Manufacturing，2011，24（1）：74-86.

［11］GHIE W，LAPERRIÈRE L，DESROCHERS A.Statistical tolerance analysis using the unified Jacobian-Torsor model［J］.International Journal of Production Research，2010，48（15）：4609-4630.

［12］ROY U，LI B，Representation and interpretation of geometric tolerances for polyhedral objects.II.Size，orientation and position tolerances［J］.Computer-Aided Design，1999，31（4）：273-285.

［13］蔡敏，杨将新，吴昭同.基于数学定义的圆柱要素形状公差数学模型研究［J］.机械工程学报，2003，39（12）：86-90.CAI Ming.YANG Jiangxin，WU Zhaotong.Mathematical model of form tolerance for cylindrical feature based on mathematic definition［J］.Chinese Journal of Mechanical Engineering，2003，39（12）：86-90.

［14］NIGAM S D，TURNER J U.Review of statistical approaches to tolerance analysis［J］.Computer-Aided Design，1995，27（1）：5-15.

［15］张为民，陈灿，李鹏忠，等.基于雅可比旋量法的实际工况公差建模［J］.计算机集成制造系统，2011，17（1）：77-83.ZHANG Weimin，CHEN Can，LI Pengzhong，et al.Tolerance modeling in actual working condition based on Jacoian-Torsor theory［J］.Computer Integrated Manufacturing Systems，2011，17（1）：77-83.

Three-dimensional tolerance analysis of engine based on Jacobian-Torsor statistical model

CHEN Hua1，TANG Guanghui2，CHEN Zhiqiang2，LI Zhimin1，JIN Sun1
（1.Shanghai Key Laboratory of Digital Manufacture for Thin-walled Structures，Shanghai Jiao Tong University，Shanghai 200240，China；2.SAIC GM Wuling Automobile Co.，Ltd.，Liuzhou 545007，China）

The working mechanism of an engine is the target of analysis in order to consider geometric tolerances which cannot be handled by traditional tolerance chains in engine assemblies.The Jacobian-Torsor model is introduced，and variations and constraints of torsors for features and their joints under the restrictions of size and geometric tolerances are built.Based on Monte Carlo simulation，three-dimensional tolerance analysis for working mechanism with a statistical way is achieved.Compared with traditional tolerance analysis methods，the method based on the Jacobian-Torsor statistical model takes more geometric tolerances into consideration and obtains more accurate results.This model can build the relationship between tolerances of parts and engine performance from tolerance chains＇perspectives.

Jacobian-Torsor；statistical method；3D tolerance analysis；working mechanism；engine

10.3969／j.issn.1006-7043.201306058

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201306058.html

TP391

A

1006-7043（2014）11-1397-06

2013-06-18.网络出版时间：2014-09-25.

国家自然科学基金资助项目（51121063，51175340）；“十二五”国家科技支撑计划资助项目（2012BAF06B03）.

陈华（1981-），男，博士研究生；金隼（1973-），男，研究员，博士生导师.

金隼，E-mail：jinsun＠sjtu.edu.cn.