饱和海床土渗流－应力耦合损伤及液化破坏规律（Ⅰ）

刘红军，李洪江，王虎，吕小辉

（1.中国海洋大学海洋环境与生态教育部重点实验室，山东青岛266100；2.中国海洋大学环境科学与工程学院，山东青岛266100）

饱和海床土渗流－应力耦合损伤及液化破坏规律（Ⅰ）

刘红军1，2，李洪江1，2，王虎1，2，吕小辉2

（1.中国海洋大学海洋环境与生态教育部重点实验室，山东青岛266100；2.中国海洋大学环境科学与工程学院，山东青岛266100）

基于重正化群理论在临界突变问题分析中的优势和岩土体的自相似特性，从海床土微观结构入手，引入三维颗粒堆积模型来描述孔隙渗流临界行为，找到了土体渗流与临界孔隙率的关系，给出了海床介质孔隙率与渗流发生的物理判别准则。在土体二元介质理论基础上，分析了饱和海床土宏观液化与微观强度的定量关系，构建了海床土体微单元破坏的重正化群模型，并对结构面断裂损伤临界概率进行了研究。研究结果表明：海床土液化是渗流－应力耦合场共同作用的结果，微单元体断裂损伤导致液化贯通带形成，进而引起海床土的宏观液化，液化贯通带的提出对研究海床土液化破坏规律有极其重要的意义。

重正化群；自相似；渗流；断裂损伤；液化带；渗流－应力耦合

土动力学中，土体液化的关键问题是如何正确测算不同条件下土中振动孔隙水压力的发展和变化规律。长期以来，国内外学者对土体液化问题进行了积极的探索，适用于不同条件的孔压发展模型相继被提出并逐步得到发展。汪闻韶等［1-5］先后提出过孔压体积应变模型、饱和砂孔压模型、应力路径模型、偏压固结模型和瞬态反应模型。其后很多学者对上述模型进行了改进和拓展，曹亚林等［6］将孔压与动荷载作用过程中消耗的能量相结合，研究了土体的孔压增量模式；石兆吉［7］分析了砂性土剪切波速与液化强度的关系；栾茂田等［8］分析了由土骨架加速度效应引起的海床动力反应特征；刘红军等［9］研究了黄河三角洲饱和粉土液化特性及孔压上升模型；陈国兴等［10-11］研究了南京细砂振动孔压的波动特性和液化大变形；孙田等［12］进行了深层海床粉质黏土动剪切模量和阻尼比试验研究等等。

然而，运用重正化群思想探讨海床土液化破坏规律的报道还鲜见发表，本文基于海床土渗流-应力耦合损伤原理采用孔隙三维堆积模型考察了渗流对液化破坏的影响，并在此基础上建立了海床土液化破坏的重正化群模型。

1 液化渗流的重正化群理论

重正化群方法最早由Wilson于1982年提出［13］，它是研究系统微观和宏观尺度的一个桥梁，基本思想是将系统内部小尺度上的涨落平均掉，再把留下的“痕迹”体现在稍大尺寸的有效相互作用强度上，通过对系统微单元作一系列自相似变换来获得系统的宏观特征表述，它可以处理包含多种长度标度的复杂问题，是一个提取主要信息而舍去次要信息的归并过程［14-15］。基于系统在临界位置（突变）的标度不变性，重正化群变换成为研究相变的有效手段，系统在临界点附近的性质与系统发生相变前的性质有很大的不同，系统在远离相变点时，内部基本上处于混乱与无序状态，逼近临界点时，关联长度增大，标度趋于不变，从而可以对系统的尺度作标度变换而不影响其性质。

研究表明，岩土体破裂过程具有随机自相似性［16］，孔隙介质液化失稳又是一种连续的几何相变，这为应用重正化群方法奠定了基础，基于标度变换的重正化群方法可以用于研究海床土体因渗流损伤而产生渐进破坏的过程，可以通过相变的临界点与重正化群变换不动点的有机结合，在不动点之下寻找海床土体的临界液化行为。

2 海床土孔隙渗流临界行为

2.1 海床土渗流的临界孔隙占有率

海床土体是一个拥有大量细观孔隙的非线性复杂力学系统，属多孔介质。研究表明，孔隙介质的渗流与孔隙空间分布的几何结构密切相关［17］，海床土渗流过程实际上是水体对孔隙空间的占据过程，渗流概率取决于孔隙在整个格子模型中的占有概率。

本文从一个孔隙分布的二维网络模型入手来揭示渗流临界孔隙占有率的含义。图1是一个将海床土体沿波浪传播方向和土层深度方向网格化了的二维重正化点阵，海床土在波浪循环荷载作用下，内部孔压会不断上升，与其相邻一定范围土体产生水头差，内部渗流现象随之发生。该渗流可分解成x和z两个方向上的渗流行为，假定点阵上的每一个格点都能以概率p被随机占据，当相邻的格点（x方向或z方向）也被占据时，这些格点就会衍生成一个“聚团”［18］。很显然，p增大“聚团”也会相应增大，当p进一步增大到某一临界值pc时，方形点阵上就会出现一无限大的“聚团”，此时认为发生了渗流相变，pc称为渗流临界孔隙占有率。

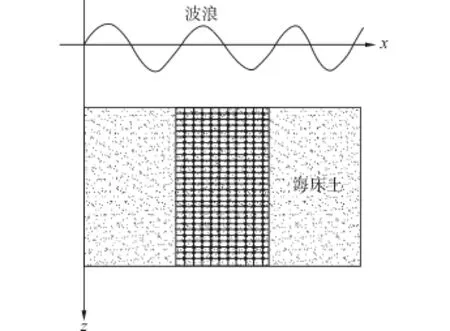
图1 海床土渗流二维网络模型Fig.1 Two-dimensional network model of seabed seepage

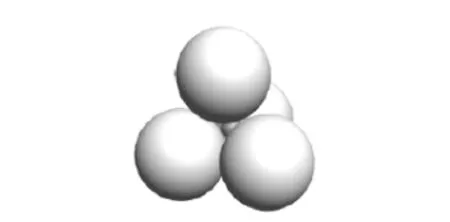
图2 最密排列Fig.2 The densest accumulation

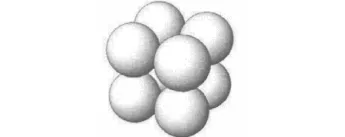
图3 最疏排列Fig.3 The most loose accumulation

海床土中的渗流发生条件取决于土体介质中相互联通的孔隙“聚团”，为更好的寻找临界渗流基本特征，将海床土介质中的孔隙简化为在空间按一定方式排列的三维颗粒堆积体，这些球体按不同尺寸、不同排列方式组成孔道和裂隙等微观构形，如图2、3分别为一种最密和最疏孔隙排列方式，经过这样的简化，复杂的渗流问题就转化为了孔隙堆积模型的占有率问题。本文将针对图2的最密排列方式应用重正化群方法讨论渗流相变点所对应的临界孔隙占有率。

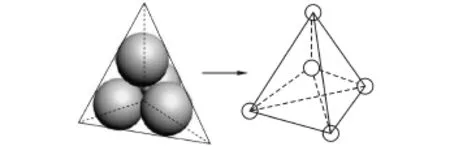
图4 最密孔隙堆积模型Fig.4 The densest pore packing model

最密孔隙堆积模型是一个正四面体模型，如图4所示，为了便于分析，将5个球体分别移置四面体的中心位置和4个顶点处，并做如下规定：至少有3个球的位置被占据，孔隙才连通，且当且只有3个球位被孔隙占据时，3个球的位置不能同时处于四面体的某一面上，否则孔隙不连通。孔隙占有率只与球体空间位置有关，与小球的尺度和体积大小无关，中心小球的被占有率与其他4个球体被占有率相同，这里假设球位被孔隙占据的概率为p0，则（1－p0）为球位被土颗粒占据的概率。

5个球位都被孔隙占据的概率为C55p05；4个球位被孔隙占据的概率为C45p04（1－p0）；3球位被占据且不同在体面的概率为（C35－4）p03（1－p0）2。故孔隙连通概率为

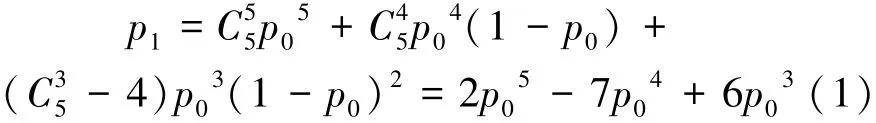
本级单元孔隙贯通后自动成为下一级单元模型的球位，球位被孔隙占据的概率变为p1，以此类推，通过不断放大观测尺度来完成重正化群变换，则下一级孔隙连通概率：

式（2）即重正化标度变换方程，重正化群一个重要目标是寻找不动点，即式（2）与pn＋1＝pn的交点，令：

解得方程不稳定不动点：p*＝0.679，这就是运用重正化变换求得的海床土渗流临界孔隙占有率。

2.2 临界孔隙率

如图5，设正四面体的棱长为L，内切球体的直径为a，则二者的几何关系满足下式：

正四面体的体积：

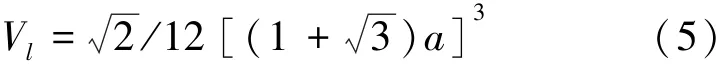
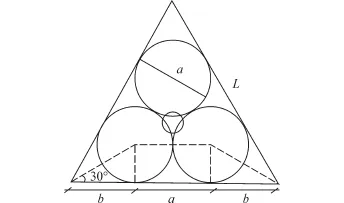
图5 正四面体与内切球体的几何关系Fig.5 The geometric relationships between a regular tetrahedron and inscribed spheres

图6 中心小圆几何尺寸Fig.6 The geometry of center small round

对于最疏孔隙堆积模型，作如下规定：至少有4个球位被占据，且当且只有4个球位被占时，4个球位不共面，孔隙才贯通，渗流才扩展。运用上述同四面体相同的分析方法，得到疏松六面体排列的渗流临界孔隙占有率：

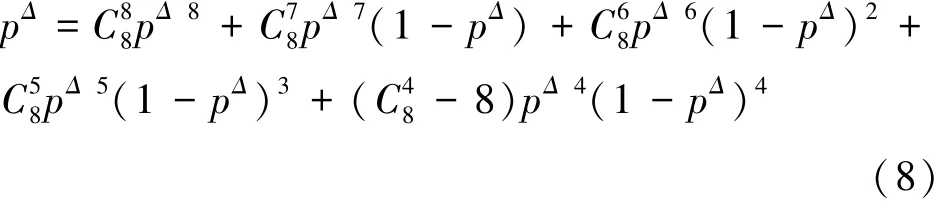
解得：pΔ＝0.416。

则最疏孔隙堆积模型的渗流临界孔隙率：

图7 最疏孔隙堆积模型Fig.7 The most sparsely pore packing model

2.3 介质孔隙率与渗流的关联

最密孔隙堆积和最疏孔隙堆积模型是海床土发生渗流的2个极端状态，有着重要的现实意义，实际的渗流孔道微观构形应该介于两者之间，基于此，给出海床介质孔隙率与渗流发生的物理判别式：

模糊渗流的意义在于：孔隙率在（0.22，0.59）区间的海床土，只有初始孔隙率大于渗流临界孔隙率的时候，渗流才发生。由于海床土所处的特殊力学环境，其孔隙率在渗流过程中是一个动态变化过程，随着波浪荷载对海床土体的改造，海床土将发生不同程度的体积应变，体应变将引起孔隙率的增减，初始不渗流的土体可能发生渗流，极易渗流的土体也可能在下一个时刻渗流终止。

1) 评价矩阵的建立.根据确定的安全管理测度，邀请p个专家对指标Aij进行打分，从而建立评价矩阵Di=[dijk]s×p.

海床土体在波浪改造作用下的孔隙比增量为

式中：VV为土中孔隙体积，VS为土颗粒体积。

根据体积应变的定义εv＝εx＋εy＋εz可知：

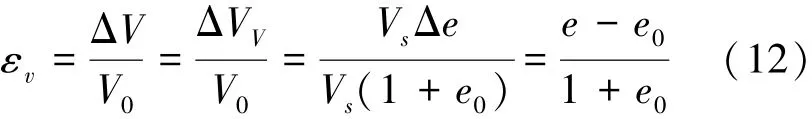
式中：V0为土体的原始体积，e0为原始孔隙比，

由式（12）、（13）可以导出孔隙率与体应变间的关系：

式中：n0为原始孔隙率。

如图8所示，伴随海床土体积变化，土颗粒重新排列牵动孔隙率的改变，孔隙率整体变化趋势随颗粒体积“膨胀”而增大，渗流扩展加剧，在这个过程中，初始不能渗流的土体会在体应变增加的作用下开始渗流；初始达到渗流临界孔隙率的土体，随着体积膨胀渗流能力增强，整体上看，海床土液化过程中伴随的渗流是一个动态变化过程，但每一个阶段发生渗流的临界孔隙率又必须遵从关系式（10）。

波浪荷载引起的土体内部孔压积累和渗流引起的孔压消散，共同影响着海床土体的液化进程，渗流具有一定的路径，渗流水体会加速土体损伤，使土体内部结构弱化，加之海床土应力状态的改变始终处于饱水环境，渗流场和应力场的耦合对分析海床液化失稳至关重要。

图8 孔隙率与体积应变的关系Fig.8 The relationship between porosity and volumetric strain

3 液化破坏的重正化群思想

3.1 二元介质单元破坏

海床土体是由结构块和结构面组成的二元介质土体［19］，胶结强的地方形成结构块，胶结弱的部位形成结构面，液化渗流渐进破坏主要是结构面相继断裂贯通形成液化带的结果，软弱液化带贯通所对应的孔隙水压力就是本文关心的液化临界孔隙水压。临界孔压的存在使土体产生瞬时相变，重正化群是解决临界突变问题的有力工具，建立如图9的海床土体液化破坏重正化群模型，按Nn＋1＝4Nn的形式将土体划分为若干小单元，也就是说，在进行标度变换时，大单元边长总是相邻小单元边长的2倍。按照自相似分形观点，每级单元与其下级或上级单元在临界状态下具有相似的性质，并假定破坏单元的剩余应力只能向临近的同级别单元传递。

图9 液化破坏的重正化群模型Fig.9 The liquefaction damage renormalization group model

重正化群模型中元胞断裂的方向是任意的，设一级单元体中至少有2个元胞断裂时，单元体破坏，由于液化剪切破坏总是沿着某一特定方向进行，为准确反映土液化的裂隙集中性，本文规定只有沿倾斜向右对角线贯通，断裂带才形成。设单元体的破坏概率为p，则（1－p）为单元未破坏概率，对单元组合中元胞破坏的情况进行分析和统计，计算后得重正化群方程：

式中：p的下标n代表重正化次数。令pn＋1＝pn＝pc解得方程的不稳定不动点为pc＝0.293，pc即为单元体破坏的临界概率。

不稳定不动点的物理意义在于，系统在到达该点时可自发地向不稳定方向发展，即孔压的累进性破坏。关联长度是用来考察任意指定单元与相邻贯通单元间距离的物理量，临界点附近液化土层中各单元关联长度可用幂律关系［20］表示如下：

式中：LP为关联长度，pc为临界概率，v为长度关联指数，定义为：v＝lnb／lnλ，b为线性标度变换因子，本模型中b＝2，λ为重正化方程（15）曲线在临界点处的切线斜率：

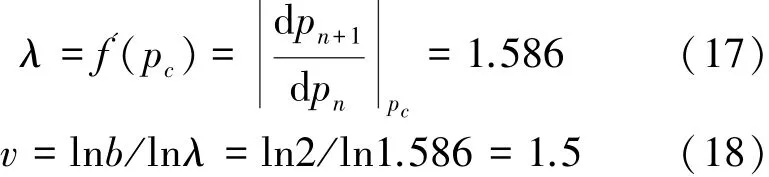
求得：

图10 关联长度与单元体破坏概率的关系Fig.10 Correlation length and unit failure probability

关联长度与单元体破坏概率的关系如图10，可知，在临界点附近，液化体系中各子单元之间的关联长度急剧增大，土体的自相似性特征凸显，这时不同体系的个性差异退居次要地位，在只考虑体系共性前提下进行一定范围的标度变换并不会影响系统的物理力学性质。其意义在于：对于液化体系发展到自组织临界状态点时，各子单元产生协同作用，体系中的土－水性质差异，颗粒排列差异，粒间胶结强度差异等被弱化，单元的断裂和贯通这一非线性行为成为共性的突出特征。因此，在临界点处，液化的复杂性可转化为简单的动力学事件进行分析和解释。从这里也可以看出，对土体液化机理的探究重心不应放在客观环境上，而应从系统内部的非线性机制出发寻找问题的答案。

3.2 结构面断裂损伤

孔隙水压上升会削弱海床土结构面的剪切强度，最终导致液化贯通带的产生，为了近似表达结构面断裂方向的任意性，重正化群模型内的元胞结构面都是以互成120°夹角向3个不同方向发展，3个结构面的力学性质完全相同。本文将分析图9的单元体破坏与结构面断裂的关联性。

图11 结构面断裂组合模式Fig.11 Structural surface fracture combined mode

如图11所示，结构面断裂有3种组合模式［bbb］［bbu］［buu］。模式Ⅰ：3条结构面都断裂［bbb］；模式Ⅱ：有2条结构面断裂［bbu］；模式Ⅲ：仅1条结构面断裂［buu］。考虑到相邻断裂面间的应力传递，模式Ⅱ可向Ⅰ演化，演化概率为α，模式Ⅲ可依次向Ⅱ、Ⅰ演化，向Ⅱ演化概率为β，演化成Ⅱ后再向Ⅰ演化的概率同为α。则液化带贯通概率为

为计算由于应力转移引起的相邻结构面断裂概率β，采用条件概率pa，b来表示一个已承受应力bσ的未破坏单元，在承受临近破坏单元转移应力（ab）σ后遭到破坏的概率：

假定结构面断裂服从Weibull统计分布［21］，即

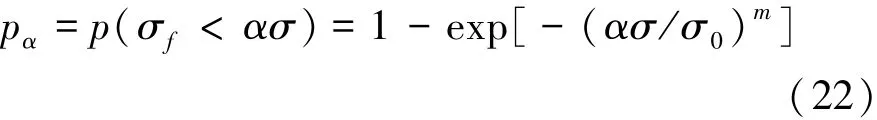
式中：pα为单元破坏强度小于应力ασ的概率；σ0为单元平均应力；m为概率分布的形状参数，也是表征土体综合特征的参数，反映土体的均匀性、密实度、孔隙率等；α为系数，当α＝1时，标准Weibull统

计为

结合式（22）、（23）得：

由于相邻结构面的性质完全相同，所以应力转移引起的相邻结构面断裂概率为

将式（24）代入式（25），液化带贯通概率被化为

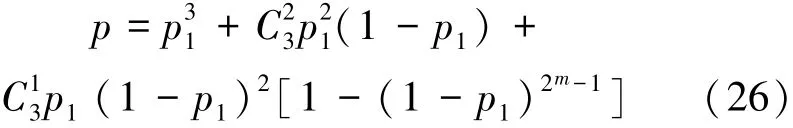
将图9单元体破坏临界概率pc＝0.293代入式（26）求解液化带贯通临界概率，即

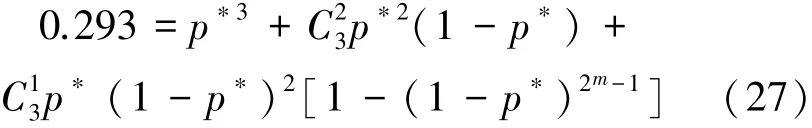
解得不同m值下的临界概率：

当m＝1，

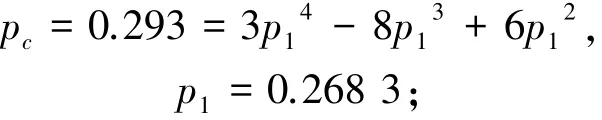
当m＝2，

当m＝3，…

m与p*的关系表征不同土质海床在循环荷载下的临界液化规律，将在后续发表的文章中给出详细的推导过程和统计验证。

4 结束语

海床土内部渗流取决于土体介质中相互联通的孔隙“聚团”，为理清海床土液化渗流机制，引入了孔隙最密和最疏三维堆积模型，并运用重正化群理论得到了两种堆积模型的渗流临界孔隙率n，指出：n＞0.59，土体极易渗流，n＜0.22土体渗流极难发生，孔隙率介于二者之间是模糊渗流状态，渗流发生与否取决于初始孔隙率是否大于渗流临界孔隙率，并指出海床土渗流是一个动态变化过程，与土体体积应变相关联。

基于重正化群理论的尺度不变性原理，通过将单元体破坏概率与重正化群方程不稳定不动点相联系，求得了单元体临界破坏概率。在单元临界破坏概率处，海床土液化的非线性复杂特征可转化为简单的动力学事件进行分析和解释。

单元体破坏是软弱结构面断裂连通的结果，通过引入Weibull分布函数对结构面断裂损伤模式进行了统计，找到了不同m取值下海床土液化贯通带的形成概率，这一概率能为解释渗流－应力耦合作用下海床土液化提供一个新的思路。

后续的研究将分析动力荷载作用下土体结构面断裂损伤与液化带贯通概率的关系，并着重探讨不同土质海床临界液化破坏规律。

［1］汪闻韶.饱和砂土振动孔隙水压力的产生、扩散和消散［C］／／中国土木工程学会第一届土力学及基础工程学术会议论文集.北京：中国建筑工业出版社，1964：224-235.

［2］SEED H B，MARTIN P P，LYSMER J.Pore-water pressure changes during soil liquefaction［J］.Journal of the Geotechnical Engineering Division，1976，102（4）：323-346.

［3］TATSUOKA I K.Undrained deformation and liquefaction of sand under cyclic stress［J］.Soils and Foundations，1975，15（1）：29-44.

［4］TOWHATA I，ISHIHARA K.Shear work and pore water pressure in undrained shear［J］.Soils and Foundations，1985，25（3）：73-84..

［5］谢定义，张建民.饱和砂土瞬态动力学特性和机理分析［M］.西安：陕西科学技术出版社，1995：3-10.XIE Dingyi，ZHANG Jianmin.Transient dynamics characteristics and mechanism analysis of saturated sand［M］.Xi' an：Shaanxi Publishing House of Science＆Technology，1995：3-10.

［6］曹亚林，何广讷，林皋.土中振动孔隙水压力升长程度的能量分析法［J］.大连理工大学学报，1987（3）：83-89.CAO Yalin，HE Guangna，LIN Gao.An energy approach for analysing the development of cyclic proe water pressure［J］.Journal of Dalian University of Technology，1987（3）：83-89.

［7］石兆吉，郁寿松.砂性土剪切波速与液化强度的关系［J］.世界地震工程，1991（3）：16-23.SHI Zhaoji，YU Shousong.Sandy soil shear wave velocity and liquefaction strength［J］.Journal of the World Earthquake Engineering，1991（3）：16-23.

［8］栾茂田，王栋.考虑土骨架加速度效应的海床动力反应及其影响因素分析［J］.海洋学报，2002，24（6）：112-119.LUAN Maotian，WANG Dong.Numerical analyses and parametric studies of dynamic response of seabed considering the effect of soil skeleton acceleration［J］.Acta Oceanologica Sinica，2002，24（6）：112-119.

［9］刘红军，王小花，贾永刚，等.黄河三角洲饱和粉土液化特性及孔压模型试验研究［J］.岩土力学，2005，26（Suppl1）：83-87.LIU Hongjun，WANG Xiaohua，JIA Yonggang，et al.Experimental study on liquefaction properties and pore-water pressure model of saturated silt in Yellow River Delt［J］.Journal of Rock and Soil Mechanics，2005，26（Suppl1）：83-87.

［10］陈国兴，王炳辉.局部排水条件下南京细砂振动孔压的波动特性［J］.岩土工程学报，2010，32（5）：767-773.CHEN Guoxing，WANG Binghui.Fluctuating characteristics of excess pore water pressure in Nanjing fine sand under partially drained conditions［J］.Journal of Geotechnical Engineering，2010，32（5）：767-773.

［11］潘华，陈国兴，刘汉龙.饱和南京细砂液化后大变形特性试验研究［J］.岩石力学与工程学报，2011，30（7）：1475-1481.PAN Hua，CHEN Guoxing，LIU Hanlong.Study of behaviour of large post-liquefaction deformation in saturated nanjing fine sand［J］.Journal of Rock Mechanics and Engineering，2011，30（7）：1475-1481.

［12］孙田，陈国兴，周恩全，等.深层海床粉质黏土动剪切模量和阻尼比试验研究［J］.土木工程学报，2012，45（Suppl1）：9-13.SUN Tian，CHEN Guoxing，ZHOU Enquan，et al.Experimental research on the dynamic shear modulus and the damping ratio of deep-seabed marine silty clay［J］.Civil Engineering Journal，2012，45（Suppl1）：9-13.

［13］VICSEK T.Fractal growth phenomena［M］.Singapore：World Scientific，1989：89-94.

［14］张德兴.重正化群在临界理论中的应用［J］.郑州大学学报：理学版，2004，36（2）：50-53.ZHANG Dexing.Application of renormalization group in critical theory［J］.Journal of Zhengzhou University，2004，36（2）：50-53.

［15］黄继成，黄彭.运用重正化群方法对沥青混合料渗透性研究［J］.同济大学学报：自然科学版，2007，35（7）：904-908.HUANG Jicheng，HUANG Peng.Permeability study of asphalt mixtures with renormalization method［J］.Journal of Tongji University：Natural Science，2007，35（7）：904-908.

［16］谢和平.分形－岩石力学导论［M］.北京：科技出版社，1996：15-22.XIE Heping.Introduction to fractal-rock mechanics［M］.Beijing：Science and Technology Press，1996：15-22.

［17］周宏伟，谢和平.孔隙介质渗透率的重正化群预计［J］.中国矿业大学学报，2000，29（3）：245-248.ZHOU Hongwei，XIE Heping.Estimation of permeability of porous media by using renormalization group［J］.Journal of China University of Mining＆Technology，2000，29（3）：245-248.

［18］STANLEY H E.Renormalization group and percolation［J］.Progress in Physics，1985，5（1）：1-65.

［19］沈珠江，陈铁林.岩土破损力学——结构类型与荷载分担［J］.岩石力学与工程学报，2004，23（13）：2137-2142.SHEN Zhujiang，CHEN Tielin.Breakage mechanics of geomaterial-structure types and load sharing［J］.Chinese Journal of Rock Mechanics and Enineering，2004，23（13）：2137-2142.

［20］施泽进，涂涛.裂隙连通性研究的重正化群方法［J］.成都理工学院学报，1997，24（3）：58-62.SHI Zejin，TU Tao.The renormalization group approach applied to study of crack conduction［J］.Journal of Chengdu University of Technology，1997，24（3）：58-62.

［21］HUDSON J A，FAIRHURST C.Tensile strength，Weibull＇s theory and a general statistical approach to rock failure［C］／／The Proceedings of the Southampton 1969 Civil Engineering Materials Conference.Southampton.Southampton，England，1969.

Study on seepage-stress coupling damage and liquefaction failure regularity of saturated seabed soil（Ⅰ）

LIU Hongjun1，2，LI Hongjiang1，2，WANG Hu1，2，LYU Xiaohui2
（1.Key Lab of Marine Environmental Science and Ecology，Ministry of Education，Qingdao 266100，China；2.College of Environmental Science and Engineering，Ocean University of China，Qingdao 266100，China）

With the advantage of renormalization group theory in critical mutation analysis and the self-similar characteristics of soil materials，the critical behavior of pore percolation and the relationships between seepage and critical porosity were found.In this paper，the critical behavior is described by the three-dimensional particle packing model from the microstructure of seabed soil.Specifically，the physical criterion is given to judge the seepage conditions associated with seabed medium porosity.Based on the binary medium theory，the quantitative relationship of macro-liquefaction and micro-strength of saturated seabed soil is analyzed.At the same time，the microbalance unit damage renormalization group model of seabed soil is built，and fracture damage critical probability of structural surface is studied.The results showed that the seabed soil liquefaction results from the interaction of seepage and stress coupling field.The formation of liquefied rupture band as a critical state is resulted from fracture damage of the micro unit cell，which leads to the macroscopic liquefaction of seabed soil.The soil liquefied rupture band method is important for the study of liquefaction failure regularity of saturated seabed soil.

renormalization group；self-similarity；seepage；fracture injury；liquefied rupture band；seepage-stress coupling

10.3969／j.issn.1006-7043.201307057

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201307057.html

TU435

A

1006-7043（2014）11-1320-07

2013-07-22.网络出版时间：2014-09-18.

国家自然科学基金资助项目（41072216）；山东省科技攻关资助项目（2014GGX104007）.

刘红军（1966-），男，教授，博士生导师；李洪江（1989-），男，硕士研究生.

李洪江，E-mail：lihongjiang55＠126.com.