Park-Ang三维损伤模型的参数确定和性能等级划分

郭进 王君杰 韩鹏 王文彪

（同济大学桥梁工程系，上海200092）

Park-Ang三维损伤模型的参数确定和性能等级划分

郭进 王君杰 韩鹏 王文彪

（同济大学桥梁工程系，上海200092）

针对Park-Ang三维损伤模型的参数取值和性能等级划分研究不足，基于试验数据，通过2轮遍历搜索，确定了参数取值；并参照已有的性能等级划分，确定了适用于Park-Ang三维损伤模型的性能等级划分标准。用一组一维试验验证了参数取值和性能等级划分对于不同加载路径的适用性；用另一组试验验证了它们对于空间受力构件的适用性。结果表明：所确定的参数和性能等级划分标准与已有的Park-Ang三维损伤模型表达式共同组成了一个完整的损伤指标，这一指标能够较好地评价不同一维加载模式或空间受力构件的损伤。

Park-Ang三维损伤模型；参数确定；性能等级；遍历搜索；加载路径

准确地评估构件在地震作用下的损伤，并对其损伤等级进行划分，这是基于性能的抗震设计方法的基本要求。地震作用下，钢筋混凝土墩柱一般是空间受力，因此建立完整的能够评价其三维损伤的模型具有重要意义。现有损伤模型都有一个共同的缺陷，即无法评价动轴力和双向弯曲作用下构件的损伤。针对这个问题，文献［1］对广泛应用的Park-Ang模型在弯矩－转角层面进行了三维拓展，使其能够考虑动轴力和双向弯曲。但是文献［1］只给出了三维拓展损伤模型的计算式，并没有指出拓展损伤模型中参数的取值和性能等级的划分。本文基于文献［1］的研究工作，在试验数据的基础上确定其参数取值和性能等级的划分标准。

1 Park-Ang损伤模型的三维拓展

Miner［2］于1945年提出了主要针对金属结构的损伤模型，此后的半个多世纪以来各国学者在该领域进行了大量的研究工作［3-6］。其中不乏适用于钢筋混凝土墩柱的广为应用的模型，例如Park等于1985年提出的变形与能量混合的损伤模型［7-8〛［9］提出了改进的Park-Ang模型，该模型在Park-Ang模型基础上做了2个改进：1）满足上下界收敛；2）考虑了不同变形幅值下相同耗能所造成的损伤不同的试验现象。

本文作者在文献［1］中对广泛应用的Park-Ang模型在弯矩－转角层面进行了三维拓展，使其能够考虑动轴力和双向弯曲。其形式如下：

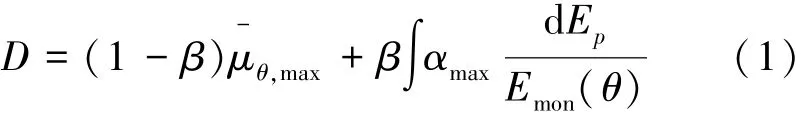
文献［1］中指出损伤模型在理论上有2个要求：

1）单调不减。钢筋混凝土构件损伤的不可逆性要求损伤值单调不减。

2）良好的预测性。损伤模型包含2部分内容：①损伤的计算式和式中参数的取值，参数的取值应有普遍的适用性；②性能状态界限值的划定。对于不同特性的构件，根据损伤表达式计算的损伤值，按照界限值判断的性能状态应该与实际结果有较好的吻合度。只有满足这一要求，才具有良好的预测性。

根据要求2），推导出如下关系式［1］：

从式（2）可以看出：β1、β2不相互独立，具有相关性，β2可由β1确定。至此，可以看出，式（1）所示的损伤模型有3个模型参数β、β1、β2，但是相互独立的参数只有2个β、β1。下面用Mo等［10］的一组试验对β、β1进行拟合。

2 参数拟合

Mo等［10］在2000年发表了钢筋混凝土悬臂柱拟静力试验的成果，共进行了9根柱的试验，均呈现弯曲破坏模式。柱净高1 650 mm，其中，水平力加载位置距离柱底1 400 mm，距离柱顶250 mm，文献［10］给出塑性铰区长度为450 mm，截面尺寸400 mm×400 mm，保护层厚度34 mm，混凝土柱回归分析所用特征参数如表1。

表1 混凝土柱回归分析所用特征参数Table 1 Characteristic parameters of the regression analysis for reinforced concrete columns

构件C1-1的弯矩－转角关系如图1所示，其中截断点是破坏点，破坏之后的加载数据不参与拟合。发生纵筋屈曲，或箍筋破坏，或纵筋破坏，或失去轴向承载能力等现象中的一个即定义为破坏。

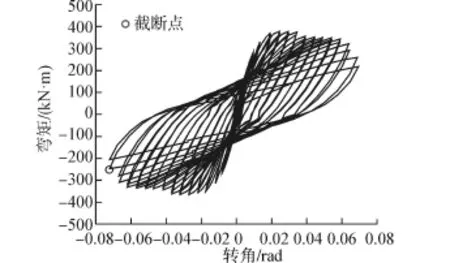
图1 构件C1-1的弯矩－转角关系Fig.1 Moment-rotation relationship for specimen C1-1

在一定取值区间内对β和β1的组合进行遍历搜索，为了减少搜索量，进行2轮搜索。第1轮搜索确定耗能项损伤系数β，第2轮搜索确定耗能修正项的指数β1。搜索间距见表2。

表2 遍历搜索所用参数取值Table 2 Parameter value for traversal search

为了评价β、β1的组合优劣性，本文采用如下述损伤值评价函数：

式中：δ为损伤偏差；Di为某β和β1取值下，第i个试件的损伤值；n为试验数目。

第1轮搜索，得到每组β、β1的损伤偏差δ。β不同取值下，各试验损伤偏差与β1之间的关系如图2。从图2可以看出，β＝0.1时，与各β1取值对应的损伤偏差均较小，因而，本文累积损伤指标中，耗能项组合系数β的取值确定为0.1，这与文献［9］研究成果中的耗能项组合系数建议值相同。

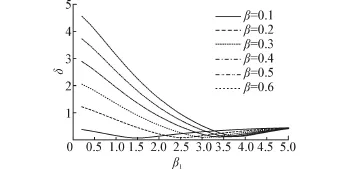
图2 第1轮搜索的损伤偏差δ与参数β1的关系Fig.2 Relationship between β1and damage deviation δ in the first round of search

在β＝0.1条件下，进行第2轮搜索，β1的搜索范围为［0.1，5.0］，步长为0.1，得到损伤偏差与参数β1之间的关系，如图3所示。从图3可以看出，β1＝1.5时，损伤偏差δ最小。因此本文取β＝0.1，β1＝1.5。

图3 第2轮搜索的损伤偏差δ与参数β1的关系Fig.3 Relationship between β1and damage deviation δ in the second round of search

由式（2）可以确定β2的取值

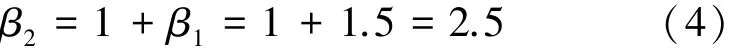
至此本文损伤模型的参数便已完全确定。

基于上述参数，运用三维Park-Ang损伤指标计算的Mo等［10］的9个试件的损伤如图4所示，破坏时各构件的损伤值如表3。

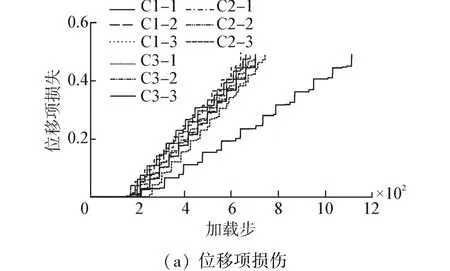
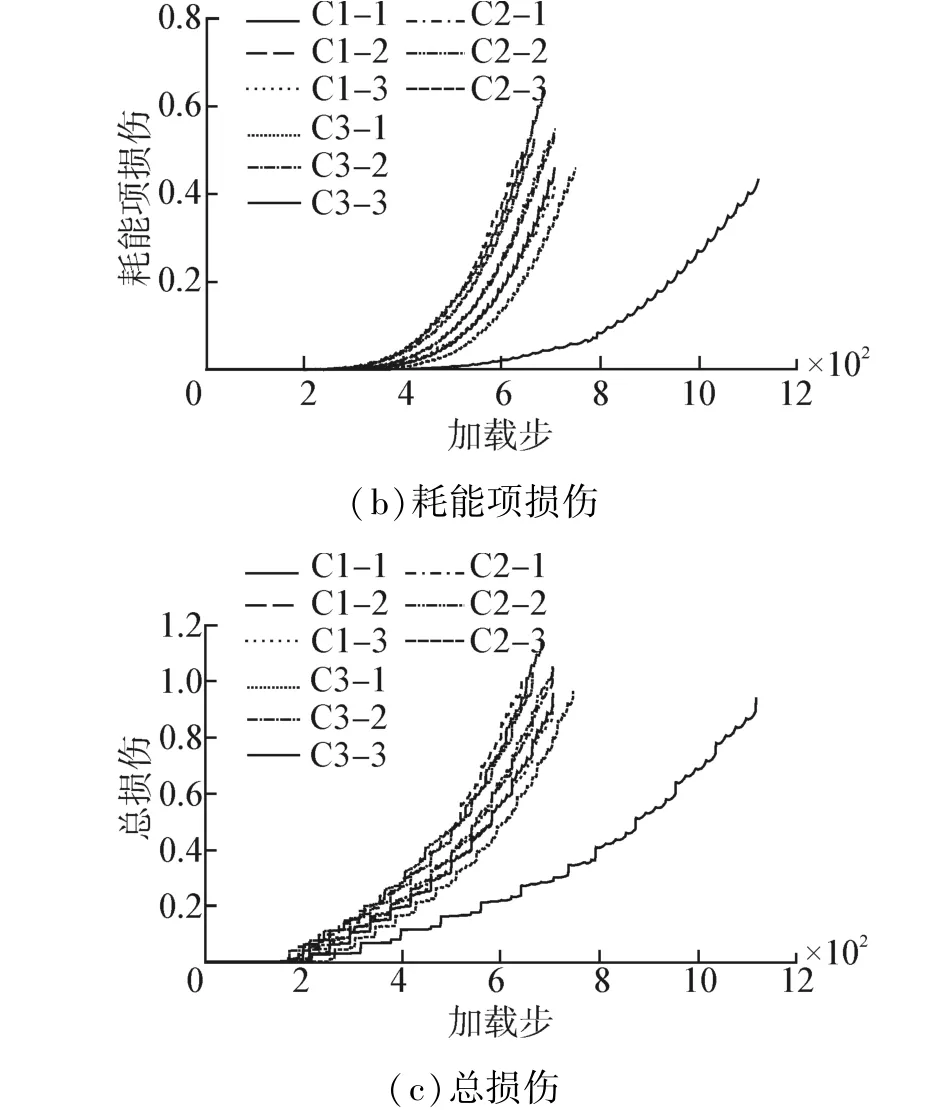
图4 三维Park-Ang损伤指标计算的Mo等［10］试验构件的损伤图Fig.4 Damage of specimens tested by Mo et al［10］using 3D Park-Ang damage model

表3 三维Park-Ang损伤指标计算的Mo等［10］试验构件的损伤值Table 3 Damage value of specimens tested by Mo et al［10］using 3D Park-Ang damage model

3 损伤等级的划分

钢筋混凝土框架结构基于性能的抗震设计允许结构在地震作用下产生一定程度的损伤，并视结构物的重要性等要求将损伤控制在可接受的范围内。因此需要较为准确地划定构件的损伤等级，这也是划定结构损伤等级的基础。同时，第1节已指出，性能等级的划分是一个完整的损伤模型必不可少的组成部分。

由于地震动本身的随机性和结构性质（如材料、几何参数）的不确定性，损伤模型各性能界限值的划分一直是各国学者的研究对象之一。关于构件累积损伤的性能等级划分，目前有多种标准。Park等［8］建议D＝0.4作为可修和不可修的损伤界限，并在1987年提出更细致的损伤划分标准［11］。

表4 Park等［11］提出的损伤等级限值与状态描述Table 4 Damage levels and state description by Park et al［11］

Stone等［12］将文献［13］的Park-Ang修正模型应用于82个圆形截面桥柱试验中，并在此基础上提出损伤划分标准，如表5。

上述Park等人在1985和1987年提出的指标，以构件具体的物理状态为标准，该等级划分方式，可在物理层面较为直观地表述构件损伤程度。但在实际操作中，该等级划分的界限表述不够严格，且不易与具体的性能指标相对应。

本文参照上述Stone和Taylor的划分方式，该方式没有将损伤等级与材料特性等指标直接对应，而是从灾后修复的角度予以划分。与上述指标相比，该指标的物理表述不够明确，但是用于直接衡量构件的抗灾变能力，具备一定的优势。

表5 Stone等［12］提出的损伤等级限值与状态描述Table 5 Damage levels and state description by Stone et al［12］

本节针对所选试验，同时计算Kunnath等［13］修正的Park-Ang损伤指标和本文指标。将与该指标界限值对应的状态，作为本文损伤指标的界限状态，取对应的损伤值作算术平均作为性能等级界限值，如表6所示。需要指出的是，由于Kunnath等［13］修正的Park-Ang指标耗能项组合系数βe的离散性较大，因此并没有根据计算公式确定βe，而是根据破坏时构件的损伤值为1来反推β的取值，即根据下式确定βe：

表6 本文的损伤界限值Table 6 Damage level limits proposed in this paper

参照Stone等［14］的修正Park-Ang指标所述损伤状态，本文损伤指标及其对应的状态表述，如表7所示。从表7可以看出，上限值接近1.00，这是9根柱子破坏时的损伤平均值，与文献［1］中确定Park-Ang三维损伤模型表达形式时设定破坏时损伤值等于1的出发点相吻合。

表7 损伤界限值与状态描述Table 7 Damage levels and state description proposed in this paper

4 一维加载的试验验证

本文选择Takemura等［14］进行的一组一维加载试验（试件编号为TP001～TP006）来建立强度退化与累积损伤的关系。该组试验6个试件的尺寸与配筋构造均完全相同，仅加载模式不同。试件为钢筋混凝土悬臂柱。截面尺寸为400 mm×400 mm，截面有效高度h0＝360 mm，加载点至地梁顶面距离L＝1 245 mm，剪跨比为3.46。混凝土强度约为35.3 MPa，纵筋采用D13钢筋，屈服强度363 MPa，全部纵筋配筋率为1.58%。箍筋采用D6钢筋屈服强度为368 MPa，箍筋间距为70 mm，体积配箍率为0.57%。试验时柱顶施加157 kN的轴压力，轴压比约为2.89%。

构件的能力为My＝191.66 kN·m，θu＝0.101 rad，EI＝1.100×1010kN·mm2。根据实验加载过程中的图片估计塑性铰区的长度lp＝400 mm。将各构件的力－位移转化为弯矩－转角关系，如图5所示。6个试件的加载路径均不相同。

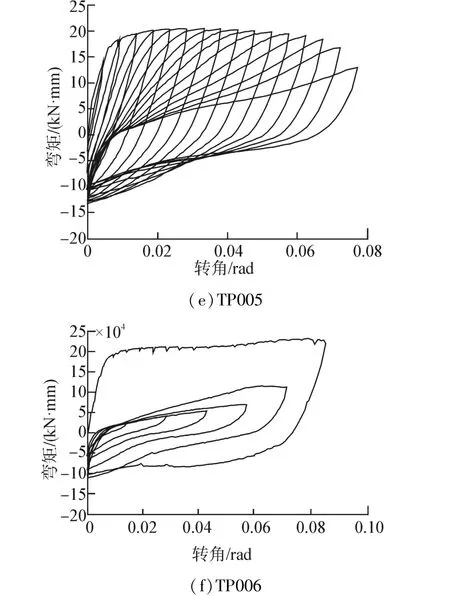
图5 TP001～TP006弯矩－转角关系Fig.5 Moment-rotation relationship for specimens TP001～TP006

基于本文提出的损伤模型和其参数，其损伤值如图6。加载终止时各构件的损伤状态如表8。

图6 TP001～TP006的损伤图Fig.6 Damage of specimens TP001～TP006

表8 TP001～TP006加载终止时的损伤状态Table 8 Damage state of specimens TP001～TP006 when loading finished

根据表7设定的性能界限值，各构件加载终止时的状态均为倒塌，这与实验结果相符。这说明本文提出的损伤模型及其参数具有较好的预测性。由于试验TP001～TP006的加载方式各异，这说明本文损伤参数和界限值能较好地用于评价不同加载模式的损伤情况。

5 空间加载的试验验证

日本川岛地震工程实验室（Kawashima Earthquake Engineering Laboratory）做了一组定轴力下柱子的弯曲试验，其加载模式包含了单向单调加载、对角加载、矩形加载、椭圆形加载、圆形加载等几种情况。该组试验测试了6个柱子，编号分别为TP-074～TP-079。其中TP-074和TP-075单向加载，其余试件是空间加载。

这6根柱子的截面是边长为400 mm的正方形，柱子从加载点至底部固结处的距离是1 350 mm。纵筋直径为13 mm，屈服屈服强度为357 MPa，配筋率为1.27%。箍筋间距直径为6 mm，屈服强度为321 MPa，体积配箍率为0.79%。混凝土强度约为29 MPa，轴压比约为3.45%。剪跨比为3.75。各个墩柱墩顶位移加载模式见图7。

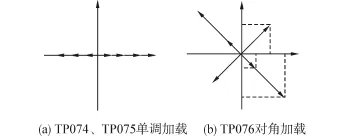
图7 试件TP074～TP079位移加载模式Fig.7 Displacement loading mode of specimens TP074～TP079

构件的能力为My＝168.075 kN·m，θu＝0.091 8 rad，EI＝1.146 3×1010kN·mm2。塑性铰区的长度lp取为208.9 mm。将试件TP074～TP079的力－位移关系转化为弯矩－转角关系，并计算其损伤，如表9所示。

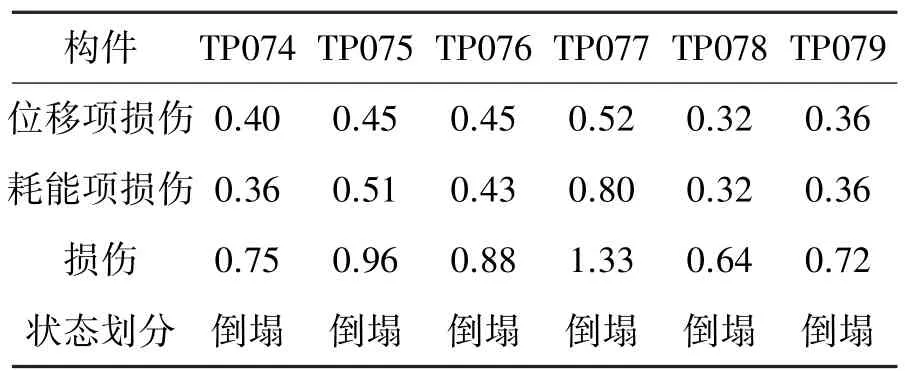
表9 TP074～TP079加载终止时的损伤状态Table 9 Damage state of specimens TP074～TP079 when loading finished

从表9可以看出，各构件的损伤值离散性比单向加载大。由于钢筋混凝土构件力学性能具有较大离散型，并且根据表7设定的性能界限值，从最终状态判定的结果来看，最终状态都是倒塌。这说明本文损伤参数和界限值对于空间加载情况也具有较好的预测性。

6 结论

本文基于实验数据，对文献［1］中三维拓展的Park-Ang损伤模型的参数进行了拟合，并对其损伤等级进行了划分，成果如下：

1）分别通过一维加载和空间加载的试验对三维损伤模型进行了验证，说明了本文给出的参数取值和等级划分能够较好地评价不同加载路径的损伤；

2）文献［1］中Park-Ang损伤模型的三维拓展形式结合本文的参数取值和性能等级划分，组成了一个能够评价三维受力构件损伤的完整指标，具有重要的工程应用价值。

基于数量更多的、具有不同特征参数（如剪跨比、轴压比、配筋率、配箍率、加载模式等）构件的试验结果，说明本文的参数和等级划分的适用范围和离散性可以作为进一步的研究方向。

［1］郭进，王君杰.Park-Ang损伤模型在弯矩－转角层面的三维拓展［J］.世界地震工程，2013（4）：141-146.GUO Jin，WANG Junjie.Three dimensional extension for Park-Ang damage model in moment-rotation level［J］.World Earthquake Engineering，2013（4）：141-146.

［2］MINER M A.Cumulative damage in fatigue［J］.Journal of Applied Mechanics，1945，12（3）：159-164.

［3］KAPPOS A J.Seismic damage indices for RC buildings：evaluation of concepts and procedures［J］.Progress in Structural Engineering and Materials，1997，1（1）：78-87.

［4］WILLIAMS M S，SEXSMITH R G.Seismic damage indices for concrete structures：a state-of-the-art review［J］.Earthquake Spectra，1995，11（2）：319-349.

［5］COSENZA E，MANFREDI G.Damage indices and damage measures［J］.Progress in Structural Engineering and Materials，2000，2（1）：50-59.

［6］COSENZA E，MANFREDI G，RAMASCO R.Use of damage functionals in earthquake engineering：a comparison between different methods［J］.Earthquake Engineering＆Structural Dynamics，1993，22（10）：855-868.

［7］PARK Y J，ANG A H S.Mechanistic seismic damage model for reinforced concrete［J］.Journal of Structural Engineering，1985，111（4）：722-739.

［8］PARK Y J，ANG A H S，WEN Y K.Seismic damage analysis of reinforced concrete buildings［J］.Journal of Structural Engineering，1985，111（4）：740-757.

［9］王东升，冯启民，王国新，等.考虑低周疲劳寿命的改进Park-Ang地震损伤模型［J］.土木工程学报，2004，37（11）：41-49.WANG Dongsheng，FENG Qimin，WANG Guoxin，et al.A modified Park-Ang seismic damage model considering lowcycle fatigue life［J］.China Civil Engineering Journal，2004，37（11）：41-49.

［10］MO Y L，WANG S J.Seismic behavior of RC columns with various tie configurations［J］.Journal of Structural Engineering，2000，126（10）：1122-1130.

［11］PARK Y J，ANG A H S，WEN Y K.Damage-limiting aseismic design of buildings［J］.Earthquake Spectra，1987，3（1）：1-26.

［12］STONE W C，TAYLOR A W.Seismic performance of circular bridge columns designed in accordance with AASHTO／CALTRANS standards［M］.Gaithersburg，MD：National Institute of Standards and Technology，1993.

［13］KUNNATH S K，REINHORN A M，ABEL J F.Computational tool for evaluation of seismic performance of reinforced concrete buildings［J］.Computers and Structures，1991，41（1）：157-173.

［14］TAKEMURA H，KAWASHIMA K.Effect of loading hysteresis on ductility capacity of reinforced concrete bridge pier［J］.Journal of Structural Engineering，1997，43A：849-858.

Parameter identification and performance classification for the three-dimensional Park-Ang damage model

GUO Jin，WANG Junjie，HAN Peng，WANG Wenbiao
（Department of Bridge Engineering，Tongji University，Shanghai 200092，China）

The selection of parameter values and definition of damage levels for the three-dimensional Park-Ang damage are not available in the existing literature.The parameters are determined based on the test data through two traversal searches.According to the existing performance levels classification method，the damage limit values for the three-dimensional Park-Ang damage model were determined.The applicability of the parameter values selection and damage levels for specimens in different loading paths is verified based on one set of one-dimensional tests.Their applicability for specimens under special force is verified based on another set of tests.The results showed that the ascertained parameters and damage levels form a complete set of damage indicators together with the expression of the existing three-dimensional Park-Ang damage model.With this damage model，damage can be accurately evaluated for structural members in different one-dimensional loading paths or spatial force.

three-dimensional Park-Ang damage model；parameter determination；performance level；traversal search；loading path

10.3969／j.issn.1006-7043.201311010

http：／／www.cnki.net／kcms／detail／23.1390.U.20140922.1645.003.html

U442.5

A

1006-7043（2014）11-1332-07

2013-11-05.网络出版时间：2014-09-22.

国家973计划资助项目（2013CB036300）；国家自然科学基金资助项目（51278373）；贵州省科技厅黔科合重大专项基金资助项目（字【2011】6014）.

郭进（1985-），男，博士研究生；王君杰（1962-），男，教授，博士生导师.

王君杰，E-mail：jjqxu＠126.com.