低重力模拟系统控制策略

朱齐丹，陈力恒，卢鸿谦

（1.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001；2.哈尔滨工业大学控制理论与制导技术研究中心，黑龙江哈尔滨150001）

低重力模拟系统控制策略

朱齐丹1，陈力恒1，卢鸿谦2

（1.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001；2.哈尔滨工业大学控制理论与制导技术研究中心，黑龙江哈尔滨150001）

为了使低重力模拟系统满足月球巡视车研发、调试的要求，系统需克服传统方法在竖直方向出现扰动时，抑制效果不好的问题，为此搭建了提供竖直方向拉力的恒张力伺服子系统。在分析关键部件工作特性的基础上，建立了范数有界参数不确定性控制对象模型，分离了标称模型与不确定性参数。根据系统的特点和巡视车测试过程中对于低重力环境的指标需求，针对性的设计了H∞控制器。通过仿真检验，控制器抑制了系统参数不确定的影响，避免了电机的机械谐振发生，并且在巡视车竖直方向加速度干扰的情况下，保证系统最大误差仅为3.4 N。

鲁棒控制；参数不确定；恒张力；低重力模拟系统；月球巡视车；控制策略

随着我国“嫦娥”探月工程的深入进行，利用巡视车对月球表面勘察、采样成为了未来的一项重要任务。为了保证巡视车动力性能可以适应月球的低重力场，需要在发射前模拟低重力环境对巡视车进行检测、调试，否则不匹配的动力性可能会破坏巡视车设备［1］，对勘探任务造成巨大影响。

在各类低重力模拟系统中，普遍存在面对竖直方向大幅扰动时，系统鲁棒性变差，甚至无法维持低重力环境的问题。例如利用气浮平台产生气体浮力抵消重力的方法，但该方法主要适用于飞行器的水平面内微重力实验［2-3］，对于巡视车实际工作时大幅颠簸无法做出性能评价。利用水中浮力与重力平衡的方法虽然可以理论上解决这一问题［4-5］，但对于巡视车防水密封性提出很高的要求，大大增加了巡视车的制造成本与难度。因此通过吊索将巡视车吊起的“悬吊法”被提出，使低重力模拟系统在机械结构上易于实现［6-7］，但由于系统缺少主动控制，面对竖直方向扰动时的抑制效果不好。所以在“悬吊法”的基础上加入双电机结构的“主动悬吊法”被提出［8-9］，然而双电机使得机械谐振点过多，导致系统带宽过窄满足不了巡视车实际测试需要；并且没有考虑系统关键参数等效弹性系数的不确定性变化，这会导致在实际工作中系统的鲁棒稳定性变差。

针对上述问题，本文在“悬吊法”的基本原理上改用单电机结构与弹簧协同工作，设计了在抑制扰动方面具有强鲁棒性优势的H∞控制器，通过仿真检验，系统工作状态平稳，控制精度满足了巡视车性能测试要求。

1 系统模型的建立

1.1 控制对象模型的建立

低重力模拟系统提供竖直方向拉力的恒张力子系统主要由弹簧、电机、减速器、抱闸、滚筒、摆杆、滑轮、拉力传感器等部分组成，其结构框图如图1。

图1 恒张力子系统结构框图Fig.1 The structure diagram of the constant tension subsystem

图1 中设吊索对巡视车拉力为T＇，巡视车地球表面所受重力为Mg，在模拟低重力环境中巡视车所受重力为Gc：

将滑轮2与摆杆视为等效摆杆，设吊索对等效摆杆的拉力为T，向上为正方向，则

由式（1）、（2）知：对Gc的控制可等价为对T的控制问题。

图1中当巡视车处于平衡状态即θ＝0时，缓冲机构利用弹簧拉伸为巡视车平衡工作点提供拉力，此时吊索对等效摆杆拉力为T0。当巡视车工作在上下颠簸的路面时，首先在电机做出反应之前，弹簧带动摆杆的摆动先抵消巡视车的部分扰动，以避免吊索张力迅速变化使得低重力系统动态误差不满足巡视车测试要求；拉力传感器测得T后与T0比较，通过控制器给电机下达指令，电机利用收放绳索补偿巡视车竖直方向位置偏移导致的T变化，使T能够稳定在T0附近，且动态误差尽量小以减少对巡视车性能测试结果的影响。

图1中弹簧张力为Ft，弹簧弹性系数为k，等效摆杆末端距离水平位置的偏移距离为xΔ，等效摆杆长度为l，等效摆杆转动惯量为J，等效摆杆工作时摆动角度为θ。在重力坐标系xgoyg中设＝等效摆杆拉力在重力坐标系为0 T[]T；摆杆坐标xboyb到xgoyg旋转矩阵为：根据胡克定律：

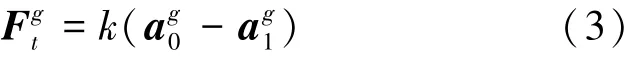
设吊索1对a1点拉力为，则＝，设向上为正方向，根据刚体定轴转动定律，对摆杆建立动力学方程：

则在平衡位置θ＝0时

设ΔT为系统工作时T距T0变化量，则

在式（5）中令等效弹性系数和等效质量分别为

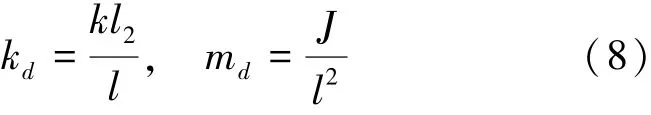
将式（6）～（8）代入式（5），得

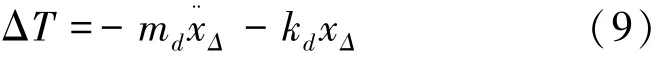
因此使T能够稳定在T0，且动态误差尽量小的控制目标可等价为：使ΔT稳定在0，且动态误差尽量小。

设xd为巡视车竖直方向的位移量，xu为电机收放吊索的位移量，l＇平衡状态下等效摆杆末端到巡视车的吊索长度，由图1吊索长度建立等式：整理可得：

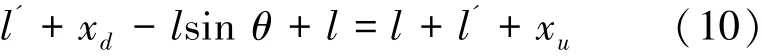
设电机对吊索收放速度为x·u，滚筒半径为r，为了方便电机对吊索进行位置控制，将交流力矩电机直驱系统工作调节在速率模式。可通过实验利用基于频率响应的模型参数辨识法，获得交流力矩电机从u到x·u的等效控制传递函数［9］：

为了方便后续的控制器设计，采用机理建模获取控制对象状态空间表达式，取x1＝xu，x2＝xu，x3＝x¨u，x4＝xd，x5＝xd，d＝x¨d，y＝ΔT，联立式（9）、（11）、（12），得：

其中：

1.2 含参数不确定性控制对象模型的建立

将k＝3 500 N／m，l1＝0.22 m，l2＝0.1 m，l＝0.23 m，J＝0.45 kg·m2代入式（8），可以得到kd＝1 552 N／m，md＝8.5 kg，实际系统中md的变化可忽略，而kd会产生ω0＝5%的波动，取巡视车加速度幅值为0.7 m／s2，频率为5 Hz时，拉力误差如图2。

图2 开环拉力误差Fig.2 Tension error in the open loop

可见巡视车竖直方向加速度及不确定性对控制吊索拉力恒定带来很大困难，为使控制器克服系统含有的参数不确定性，需建立含参数不确定的控制模型。

建立含参数不确定性控制模型主要有建立多面体系统和建立范数有界参数不确定系统2种方法。多面体系统对于参数分析是一种很好的途径，然而在控制设计上并没有好的方法［10］。而范数有界模型处理方法则可以有效的与控制器设计结合，因此采用范数有界模型处理参数不确定性。

其中：

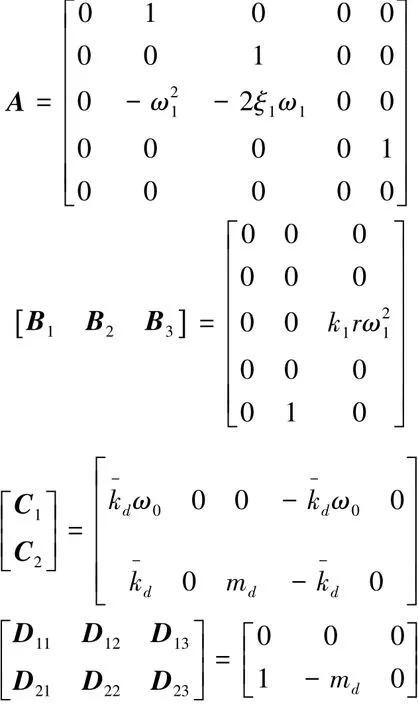
为了方便分析式（14）可用图3来表示，通过引入输入项ω与输出项z1，将不确定部分与系统标称模型分离，使得控制器在对系统性能做出改善的同时可以对不确定参数变化时的系统响应的变化做出抑制。将各参数数值0.1 m，ξ1＝0.3，kd＝1 552 N／m，md＝8.5 kg代入式（14），并将系统化为最小实现：

图3 含范数有界参数不确定性控制对象模型Fig.3 The controlled object model of norm bounded parameter uncertainty

2 控制器策略的选择与设计

2.1 控制策略的选择

针对系统面临的巡视车竖直方向加速度的干扰，电机部分机械谐振问题，缓冲机构参数不确定，控制策略选择上需以结合系统不确定性和外部扰动的抑制为重点确定控制器类型。

H∞控制是近年来在工业实际中应用较广的一种控制策略［11］，它可以将外部扰动与本身模型的不确定性转化为同一形式，并通过传递函数Hωz（s）将其被调输出的H∞范数最小为基本思想，使得在抑制扰动及不确定性问题上拥有很好的效果；H∞控制器在求解过程中利用小增益定理保证闭环系统的稳定性，因此通过H∞控制器综合出的系统往往具有良好的鲁棒稳定性，所以H∞控制成为了低重力模拟系统控制器设计的首选。并且Matlab软件为H∞控制提供了专门的函数，使得控制器在求解过程中，摆脱了繁杂的公式计算，简化了控制器的设计。

2.2 H∞控制器的设计

将控制系统实现框图如图4转化为H∞控制的标准结构如图5所示，K为待求的控制器，z为待设计的系统被调输出，P为系统广义控制对象，P由系统标称模型和加权函数组成，首先设计它的结构框图如图6，根据系统存在抑制参数不确定性、电机的高频谐振及外部干扰上的性能需求，选取了被调输出：z1为不确定性输出，z2为控制电压的被调输出，z3为吊索拉力变化的被调输出；相应的加权函数上选取：wd为干扰的加权函数，wu为对控制输入的加权函数，wf为吊索张力变化加权函数。加权函数的选取将直接决定系统能否满足月球巡视车测试时的要求。

图4 控制系统实现框图Fig.4 The block diagram of control system

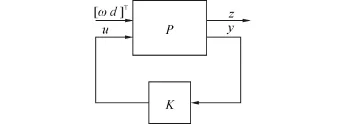
图5 H∞控制结标准结构Fig.5 The standard structure of the H∞controller

图6 恒张力伺服系统广义控制对象PFig.6 The generalized control object P of the constant tension servo system

加权函数wd用来模拟干扰的输入，为了使控制器能抑制干扰最严重的情况，wd取巡视车工作时竖直方向加速度幅值最大值，即wd＝0.7。

加权函数wf作用是在巡视车竖直方向加速度频率段内即f≤5 Hz，惩罚巡视车干扰对吊索拉力变化量影响，使得d到y的幅频特性在f≤5 Hz尽量小，而对工作频段外幅频特性可能的升高不做限制，因此设计wf为低通滤波器形状传递函数：wf＝

加权函数wu用来惩罚控制输入u的高频信号，以避免执行机构发生饱和，而对u的低频信号不做限制，因此wu设计为高通滤波器形状的传递函数，结合系统带宽可实现性及机械谐振频率点，将其转折频率设置为100 rad／s。为了保证尽量保证H∞最优指标γ≤1，以确保综合出的控制器使系统满足小增益定理［10］保证系统的鲁棒稳定，对wu的增益进行调试，确定

利用Matlab提供的hinflmi函数，可以通过编程求得此时H∞最优指标γ＝0.935 4，满足小增益定理，控制器K的Bode图如图7。

图7 控制器K的Bode图Fig.7 The Bode diagram of the controller K

由图7知，控制器在低频段增益较大，以抑制巡视车工作时带来的干扰。在300 rad／s附近出现明显的陷波特性，与电机谐振峰值处频率相近，与限制控制器带宽方法结合，共同抑制机械谐振对系统的影响。控制器带宽与文献［9］相比，得到了明显增大，减少了控制器的保守性。

为了检验系统鲁棒稳定性，利用wcgain函数得到不确定参数对闭环系统影响最严重时的参数值kd＝1 629.6 N／m，并将其代入闭环系统状态矩阵A＇中，计算A＇特征值为

因此可验证控制器使得系统鲁棒稳定。

3 控制器鲁棒性仿真检验

巡视车竖直方向加速度模型可表示为x¨d＝ Asin（2πft），其中｜A｜≤0.7 ms2，频率f≤5 Hz。为了保证巡视车性能测试时的准确性，要求低重力模拟系统的动态误差｜ΔT｜在5 N以内。在Matlab软件里为了检验系统在实际工作中的鲁棒性，仿真中加入模拟拉力传感器的噪声模块，传感器采样频率600 Hz，方差为0.01N2。取干扰最严重的情况，即A＝0.7m／s2，f＝5 Hz，仿真时间为10 s，仿真结果如图8所示。

图8表明在干扰最严重情况下所设计的控制器使系统保持稳定。在图8（a）中｜ΔT｜≤3.4 N，控制精度得到了很好的保证。图8（b）表明面对高频扰动时，电机的输入电压不足0.8 V，而电机的工作电压范围为－10～＋10 V，因此干扰对于电机工作负担很轻，减轻了电机的磨损。图8（c）在干扰频率最高时，绳索收放速度最大为0.05 m／s，电机输出未出现幅值“堵塞”现象，表明电机可以跟上巡视车对系统的扰动。

由图9对比可知，对于不确定性Δ的变动，系统保持稳定，且ΔT变化几乎没有受到影响，表明控制器很好地抑制了不确定性参数变化对系统的影响，因此系统具有良好的鲁棒性。

图8 干扰最严重时系统关键信号的响应Fig.8 The key signal responses of the height interference

图9 kd的变动时吊索拉力变化Fig.9 The sling tension changes when kdchanges

图10 扫频模式下系统关键信号响应Fig.10 The key signal system response in the frequency sweep mode

取巡视车工作在指标A＝0.7 m／s2时，对系统扫频，频率范围为巡视车工作时竖直方向加速度频率变化范围0.1～5 Hz，仿真时间10 s。由图10（a）可知，在巡视车工作的加速度频率范围内，吊索拉力最大动态误差为3.4 N，满足了巡视车测试对与低重力模拟系统的要求。由图10（b）可知，控制电压在各频率段处于工作电压范围内，保证了电机正常工作，并且输入电压在高频段变小，验证了弹簧吸收巡视车的高频扰动的作用，减轻电机在高频段的工作压力。

4 结束语

对于传统低重力模拟方式在面对巡视车竖直方向大幅颠簸时，低重力效果差、精度变低、不稳定的问题。本文针对性的建立了控制对象模型，并实现了参数不确定问题的分离；对于带宽有限及干扰抑制的要求，设计了具有强鲁棒性优势的H∞控制器；在仿真检验中，控制器不仅抑制了巡视车竖直方向大幅度颠簸对于稳定性以及精度的影响，并且保证了参数不确定性下的系统鲁棒性；通过对于控制输入的监控，该控制器可以确保系统的可实现性；在扫频模拟巡视车加速度干扰的条件下，系统的最大误差不超过3.4 N。

由于本文没有考虑系统内部存在的摩擦，吊索谐振等因素，使得实际物体和理论模型仍然存在差别，未来可以结合上述因素对控制器进行进一步的完善，并在实验条件允许下搭建实际系统，可以为月球巡视车的性能调试提供更大的帮助。

［1］肖福根，叶培建.月球探测工程中的月球环境问题［J］.航天器环境工程，2006，23（1）：1-3.XIAO Fugen，YE Peijian.Issues about lunar environment in lunar exploration project［J］.Spacecraft Environment Engineering，2006，23（1）：1-3.

［2］齐乃明，张文辉，高九州，等.空间微重力环境地面模拟试验方法综述［J］.航天控制，2011，29（3）：95-100.QI Naiming，ZHANG Wenhui，GAO Jiuzhou，et al.The primary discussion for the ground simulation system of spatial microgravity［J］.Airspace Control，2011，29（3）：95-100.

［3］ISOBE T，NAGASAKA K，YAMAMOTO S.A new approach to kinematic control of simple manipulators［J］.IEEE Transactions on Systems，Man and Cybernetics，1992，22（5）：1116-1124.

［4］姚燕生，梅涛.空间操作的地面模拟方法-水浮法［J］.机械工程学报，2008，44（3）：182-188.YAO Yansheng，MEI Tao.Simulation method of space operation on the ground-buoyancy method［J］.Chinese Journal of Mechanical Engineering，2008，44（3）：182-188.

［5］姚燕生.三维重力补偿方法与空间浮游目标模拟实验装置研究［D］.合肥：中国科学技术大学，2006：56-80.YAO Yansheng.Research on 3-D gravity compensation and equipment of space floating objective simulation［D］.Hefei：U-niversity of Science and Technology of China，2006：56-80

［6］SATO Y，EJIRI A，IIDA Y，et al.Micro-G emulation system using constant-tension suspension for a space manipulator［C］／／Robotics and Automation，1991.Sacramento，America，1991：1893-1900.

［7］WHITE G，XU Y.An active vertical-direction gravity compensation system［J］.IEEE Transactions on Instrumentation and Measurement，1994，43（6）：786-792.

［8］王连明.低重力模拟系统控制算法的研究［D］.哈尔滨：哈尔滨工业大学，2010：10-30.WANG Lianming.Research on control algorithm of microgravity simulating system［D］.Harbin：Harbin Institute of Technology，2010：10-30.

［9］王乐.低重力模拟器吊索张力控制算法研究［D］.哈尔滨：哈尔滨工业大学，2011：11-20.WANG Le.Control algorithm on the sling tension of low-gravity simulating system［D］.Harbin：Harbin Institute of Technology，2011：11-20.

［10］刘志康，姚郁.线性鲁棒控制［M］.北京：科学出版社，2013：277-300.

［11］俞立.鲁棒控制-线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002：44-59.

The control strategy of low gravity simulation system

ZHU Qidan1，CHEN Liheng1，LU Hongqian2
（1.College of Automation，Harbin Engineering University，Harbin 150001，China；2.Center for Control Theory and Guidance Technology，Harbin Institute of Technology，Harbin 150001，China）

In order to make the low gravity simulation system meet the research and debugging of a lunar rover，the system needs to overcome the problem that the system cannot work well when the disturbance is in vertical direction.A constant tension servo system for providing vertical tension is set up.The working characteristics of key components are analyzed and the mathematical model of the key components is established，which includes the normbounded parameter uncertainty.The nominal model and the uncertainty parameter were separated.According to the characteristics of the system and the index requirements of the lunar rover testing process for low gravity environment，the H∞controller of the system is designed for this purpose.It is verified that the controller solves the problem of the parameter uncertainty and avoids the mechanical resonance of the motor.The system ensured that the error is less than 3.4 N under the interference of the vertical acceleration of the lunar rover.

robust controller；parameter uncertainty；constant tension；low gravity simulation；lunar rover；control strategy

10.3969／j.issn.1006-7043.201309039

http：／／www.cnki.net／kcms／detail／23.1390.U.20140925.1517.001.html

TP273

A

1006-7043（2014）11-1384-06

2013-09-11.网络出版时间：2014-09-25.

国家自然科学基金资助项目（61175089，61203255，61021002）.

朱齐丹（1963-），男，教授，博士生导师.

朱齐丹，E-mail：zhuqidan＠hrbeu.edu.cn.