一快速有效地计算肥大型船体运动的方法
黄明汉,邹志利,张文忠,张庆河
一快速有效地计算肥大型船体运动的方法
黄明汉1,2,3,邹志利3,张文忠1,张庆河2
(1中交天津港湾工程研究院有限公司中国交建海岸工程水动力重点实验室,天津300222;2天津大学建筑工程学院,天津300072;3大连理工大学海岸和近海工程国家重点实验室,
辽宁大连116024)
文章对船体的水动力和运动提出了一个快速有效的计算方法。该方法考虑了船体周围流场的三维效应,既适用于细长型船体,也适用于肥大的船型。该方法的出发点是将船体剖面用具有相等面积的等效矩形代替,并将流场划分为船底与水底之间的内场和船侧面之外的外场。对内场,采用简单的解析解;对外场,由于剖面是矩形的,所以可采用在船体水面周线上分布源汇的简单的源汇分布法。对内外场进行耦合匹配进行求解。通过与三维源汇方法计算的结果比较,验证了文中计算的快速性和有效性。
波浪力;船体运动;肥大型船体;源汇分布法
1 引言
近年来,随着人类对海洋资源开发利用及国际间贸易往来的规模日益扩大,海上交通运输也日益频繁,所以港内船舶运动问题的研究一直是重要研究课题。其研究对船体和港口的安全性及港内安全作业情况具有重要意义。由外海传来的波浪会使船舶做6个自由度的运动,包括纵荡、横荡、垂荡、横摇、纵摇和艏摇。对波幅不是很大的情况,有时却会使船体产生较大幅度运动,严重的会导致港内作业不能正常进行,会危及到船体和港口的安全。因此,研究港内船体在波浪中的运动对船舶正常作业及安全靠泊都具有重要意义。研究波浪中船体运动的方法有切片法和三维源汇方法,其中三维源汇方法是一比较成熟的方法。然而三维源汇方法[1-4]由于剖分网格多、占用计算机内存大,计算耗时长,难以满足工程快速计算的需要。由于经济的飞速发展,细长型船体不能满足当前生活和生产的需求,越来越多的出现超大型船体以及肥大型船体。因此,需要发展更为简单高效的计算港内波浪与船体作用问题的方法。
2 波浪中船体运动简单高效的计算方法
将Lean和Bowers等[5]提出的仅适用于细长型船体的方法扩展到一般三维船体波浪中运动的计算。Lean等给出的计算模型是对船体横向剖分单元,并把横向剖分单元的每一剖面用具有相等面积和相同吃水的等效矩形代替,将流动分为船底面和水底之间矩形区域的内场、船体侧面以外的外场。内场流动假设为沿船宽方向的二维流动,外场采用将速度势沿水深作傅立叶展开并在水线面周线上布置源汇来确定。由于采用了这些简化,所以该方法计算效率高。黄明汉和邹志利[6-7]给出了该方法的推导和在多物体耦合计算上的拓展及应用分析。但由于该方法对内场只沿船体横向剖分,忽略了船体纵向的流动,所以在处理肥大型船体问题上这种方法就不再适用。本文所提出的方法克服了以上问题,将Lean等的方法扩展应用于考虑一般三维流动,即对船体横向和纵向同时剖分。
2.1 速度势的分解和定解条件
为了计算船体水动力问题,建立如图1所示的坐标系。该坐标系oxyz固结在船体上,取o点位于船体重心G处,x轴平行于船长方向,z轴向上。取β为波向角,船迎浪时β取0°。
在波浪与船体相互作用的研究中,流体介质在绝大部分情况下都可以认为是均匀、不可压缩和无粘性的理想流体。考虑入射波为规则波,采用线性理论,在频域内求解。船舶在波浪中做6个自由度的摇荡运动,位移为:

式中:Re表示取实部,j=1,2,…,6对应于纵荡、横荡、垂荡、横摇、纵摇和艏摇,ζj为第j模态下的运动幅值,由于其为复数,所以还包含了运动的相位。定义流场中速度势的梯度为流场中该点速度的负值:


图1 坐标系的描述Fig.1 Description of coordinates
式中:V=u,v,()w,并把速度势写成空间分量和时间分量分离的形式:

将速度势空间分量Φ可分解为:

式中:在外场:φ0是入射势,φj是船做第j模式运动时的辐射势,φ70是绕射势;在内场:φuj是船做第j模式运动时的内场辐射势,φu7是绕射势引起的内场速度势。ζj是船做第j模式运动时的运动幅值,这里为了书写方便把内场和外场的辐射势和绕射势写成同一个表达式φj和φu7,即增加一个编号j=7。设入射波是单向的规则波,其速度势为:

式中:ζ0和ω分别为入射波波幅和圆频率,g为重力加速度,k0是波数,满足的色散关系ω2=gk0tanhk0h,h是水深。
在频域内,根据线性势流理论,内外场的辐射势和绕射势应该满足控制方程和边界条件,其φj和φuj满足的定解条件是:

式中:υ=ω2/g,r2=x2+y2,R2=x2+y2+z2,S0是船体的湿表面,n(j为物面上某点在局部坐标系中的广义法向矢量,为物体表面单位法向矢量(指向流体外部),n( x,y,z),D为船体吃水,条件[M]是船体内外场速度势的在交界面S′上的匹配条件。
2.2 内场和外场的划分及计算网格
下面首先给出本计算模型内外场的划分方法。该方法分别沿船横向(船宽方向)和纵向(船长方向)将船体进行剖分,见图2。在船体剖分时,首先把船体沿横向剖分为n个截面,每个截面形成上下对称的2个节点,所以编号是关于船体纵轴(x轴)上下对称的。即1对n+1,2对n+2,…,n对2n,在水线面周线上形成对称的2n个网格点,周线上有2n个单元。纵向剖分的网格点也采用与横向剖分相同的2n个网格点,但纵向剖分采用连接关于船横轴(y轴)两个纵向对称的网格节点来实现,如图2所示,这样纵向剖分也有n个截面及周线上2n个单元。但横纵剖的节点编号顺序是不一样的,如图2所示。

图2 物体水面周线纵向和横向同时剖分Fig.2 Grid distribution along the contour of body water surface
对横向和纵向剖分所得到的船体剖面用具有相等面积和相同吃水的等效矩形代替,如图3和图4所示。将船体周围流动分为船底面和水底之间的内场、船体侧面以外的外场。

图3 船横剖面(虚线)和其计算中的代替剖面(实线)Fig.3 Ship cross section and equivalent section in calculations

图4 船纵剖面(虚线)及其计算中的代替剖面(实线)Fig 4 Ship longitudinal section and equivalent section in calculations
对于矩形船体这一特殊船型,其横向和纵向单元节点就不再重合,如图5所示。纵向剖分n1个截面,每个截面有2个左右对称的节点,对应两侧边界有2n1个单元;横向剖分n-n1个截面,对应两侧边界有2(n-n1)个单元,其节点编号也按上下对称或左右对称排列,如图5所示。
通过以上方法的处理使得本方法不仅适用于细长船体,也可适用于具有较肥大船艏船艉的船型。对于港口内或近岸水域船舶,船底和水底之间间隙相对水深一般较小,所以对内场的流动可采用简单的方法处理,以解析解表达。对外场,由于对船体剖面采用了矩形进行近似,所以也可采用简单的办法处理,即可将计算流场速度势的格林函数沿水深作本征函数展开,这样仅需要在船体水面周线上布置源汇,使得通常的三维源汇分布法需要求解源汇在整个船体的分布转化为仅需要求解源汇在船体水面周线上的分布,这样可以大大减少计算量。
2.3 内场速度势的确定
由于船体同时进行横向剖分和纵向剖分,内场的速度势将由横向剖分速度势和纵向剖分速度势加权叠加得到,这样就可以将其与外场速度势在内外场交界面上进行匹配求解。通过横向剖分和纵向剖分速度势Φa和Φb可以确定内场总的速度势φ为:

上式只适用于船底面速度∂ξ/∂t不为零的情况(即船体做垂荡、横摇和纵摇的情况),对∂ξ/∂t=0的情况(即船纵荡、横荡和艏摇及绕射的情况),以上加权叠加不再适用。但数值计算表明,对速度势也需要采用类似的叠加。这将在下面给出统一处理。

图5 矩形物体水面周线网格划分Fig 5 Grid distribution along the contour of rectangular body water surface
由于人为的将三维流动分解成两个垂向二维流动,这样对于物体尺度长宽比接近时会引入误差,其横向和纵向速度势叠加并不等于总的速度势。对于这一误差,可以通过对以上加权所得到的内场速度势进行修正,我们取修正系数L2/L2+B2()及qa和qb,下面针对模型验证的计算结果表明,选取这样的修正系数所得的计算结果与三维源汇的计算结果符合。这样总的内场速度势及横向速度势和纵向速度势可以写为:

2.4 外场速度势的确定
外场速度势可采用源汇分布法来表达,这种方法基于把船体剖面用等效矩形代替,即可将计算流场速度势的格林函数沿水深作傅立叶展开,这样仅需要在船水面周线上布置源汇。于是外场速度势的可以表示为

式中:Γ为物体水面处的周线,点p代表场点水平坐标p=(x,y),点q为源点水平坐标q=(xq,yq),σj0(q)和σji(q)代表当船体进行j模态摇荡运动时船体水面周线上q点处的源强,是第一类汉克尔函数)是变型第二类贝塞尔函数分别满足关系式k0tanhk0h=ω2/g和kitankih=-ω2/g。源强σj0(q)和σji(q)可通过内外场速度势代入物面条件[S]和匹配条件[M]中求解出。
2.5 运动方程的求解
在流体作用力已知的条件下,利用刚体运动的一般理论,在微幅运动的条件下可建立起船体在波浪上的运动方程:

式中:mij为船体的广义质量,Xj是在j模态下的瞬时位移。以上六个联立方程形成方程组,求解该方程组可得每个船体的运动响应。
本文中附加质量μii、阻尼系数λii(下标i对应运动模态)、波浪干扰力Fi(下标i对应力的方向)、周期T的统一按下式作无因次处理:

式中:V表示排水体积,S表示物体水线面面积。本文图表中无因次处理均按上式表达,图中不再作说明。
3 模型验证
为了验证以上数值模型,下面将分析计算结果与三维源汇方法计算的计算圆型浮体、椭圆型浮体的结果进行比较。
3.1 圆型浮体的计算
本节通过计算圆型浮体与三维源汇方法的结果比较,来验证本方法的有效性。其中计算的圆型浮体的主尺度,见表1。本方法在圆型浮体水面周线上剖分120个单元,即在图2中n取60,横向剖分和纵向剖分共计算240个单元。而三维源汇方法在圆型浮体周线上取的单元数也是120个,其侧面单元720个,底面单元720个,共计算1 440个单元,见图6。坐标系取图1中单体坐标系,波浪45°入射,水深为13 m,分别采用本方法、横剖方法和三维源汇方法计算圆型浮体的附加质量、阻尼系数、波浪干扰力和运动响应,如图7-10所示。
从图7中,可以看出圆形浮体的附加质量在各个方向上本方法和三维源汇方法计算结果符合较好,而横剖方法由于仅横向剖分单元,仅横荡计算结果与其他两个方法计算结果一致。说明横剖方法的横荡计算结果与三维源汇方法计算结果的误差较小,但在其他方向上计算误差较大。所以本方法由于通过对浮体横向和纵向同时剖分,克服了横剖方法处理肥大型浮体的不足。同理,可以从图8、图9和图10中看出,横剖方法的横荡计算结果误差较小,在其他方向上误差较大,而本方法和三维源汇方法计算结果符合较好。这是因为横剖方法认为流场沿浮体纵向变化较小,浮体周围流场的求解只在浮体各横剖面内进行。而对于这种较肥大的浮体,浮体纵向的流场变化是不可以忽略的,所以横剖方法计算圆型浮体是不准确的。本方法正是考虑到横剖方法不能很好地计算这类较肥大的浮体,所以通过对浮体同时横向剖分和纵向剖分,通过一定的加权叠加,得到浮体周围的三维流场。
下面从计算效率上来进行分析。本方法和三维源汇方法都是在同一电脑上计算的,电脑配置是Intel Core 2 Duo CPU T8100 2.1 GHz 2.09 GHz 1.99 GB的内存。本方法计算45个频率的规则波用时1分钟22秒,三维源汇方法计算45个频率的规则波用时19分钟10秒。从计算用时来看,本方法与三维源汇方法相比,计算快,效率高。

图6 圆型浮体侧面和底面的三维源汇方法的单元划分Fig.6 Grid distribution along the bottom and side of circluar floating body by three-dimensional source-sink distribution method

表1 圆型浮体的主尺度Tab.1 Floating body details

表2 椭圆型浮体A的主尺度Tab.2 Floating body A details

表4 椭圆型浮体C的主尺度Tab.4 Floating body C details

表3 椭圆型浮体B的主尺度Tab.3 Floating body B details

图7 圆型浮体的附加质量Fig.7 Added mass of circluar floating body


图8 圆型浮体的阻尼系数Fig.8 Damping coefficients of circluar floating body

图9 圆型浮体的波浪干扰力Fig.9 Wave exciting force of circluar floating body


图10 圆型浮体的运动响应Fig.10 Responses of circluar floating body
3.2 椭圆型浮体的计算
上一小节计算的是特殊圆型浮体,其中浮体长和浮体宽比L/B=1:1。本节将计算三个椭圆型浮体,其中浮体长和浮体宽比L/B=分别是4:1、3:1和2:1,这三个椭圆型浮体A、浮体B和浮体C的主尺度,如表2、表3和表4。坐标系取图2.1中单物体坐标系,波浪入射角度均为45°,水深为13 m,分别计算了三个椭圆型浮体的的附加质量、阻尼系数、波浪干扰力和运动响应,并且给出了与三维源汇方法计算结果的比较,如图11-14,横坐标和纵坐标的无因次处理见2.6.3节。本方法在三个椭圆型浮体水面周线上都剖分120个单元,即在图2中n取60,横向剖分和纵向剖分共计算240个单元。
从图11-14可以看出,对纵荡、横荡和艏摇,本方法和三维源汇的水动力系数,波浪干扰力和运动响应计算结果吻合得较好,误差在2%以内。对垂荡、横摇和纵摇,本方法和三维源汇的水动力系数,波浪干扰力和运动响应计算结果有一定误差,但是趋势是一致的。其中,对垂荡,本方法与三维源汇的结果在大小上相差不大,有5%左右的误差。对横摇,在浮体长宽比较大的时候,误差较小。当浮体长度和浮体宽度比逐渐变小,并且接近于1时,误差也逐渐增加,最大误差在20%左右。对纵摇,与横摇方向的情况正好相反,物体的长宽比较大时误差较大,长宽比接近1时误差较小。

图11 椭圆型浮体的附加质量Fig.11 Added mass of elliptical floating body

图12 椭圆型浮体的阻尼系数Fig.12 Damping coefficients of elliptical floating body
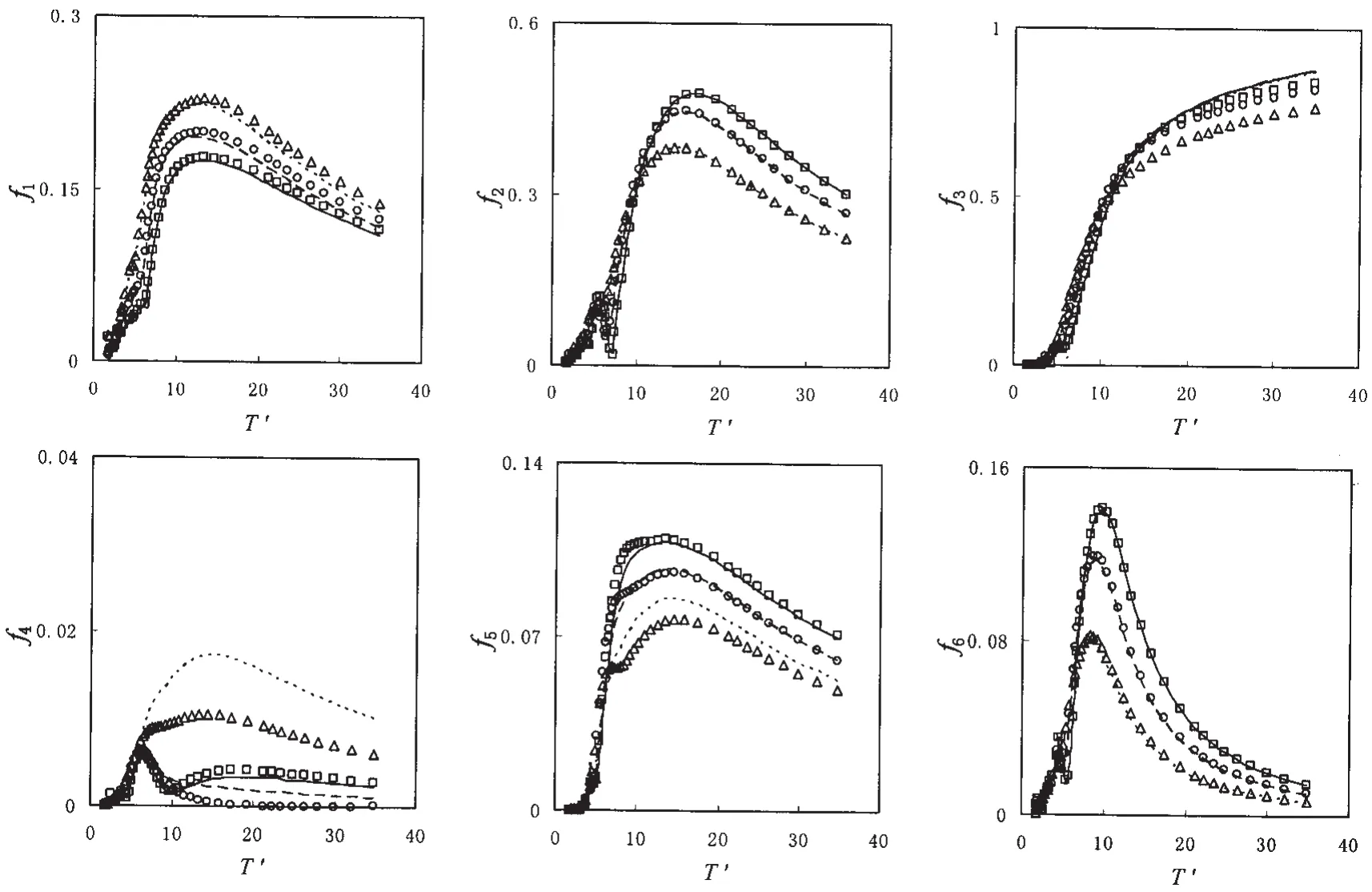
图13 椭圆型浮体的波浪干扰力Fig.13 Wave exciting force of elliptical floating body

图14 椭圆型浮体的运动响应Fig.14 Responses of elliptical floating body
4 结论
由于同时采用横向剖分和纵向剖分,使得本方法可以应用于任意形状船体,即不仅适用于细长船体,也可适用于具有较肥大船艏船艉的船型。在算例中,本方法通过计算圆型浮体、椭圆型浮体与三维源汇方法计算结果的比较,说明方法中横剖和纵剖的加权系数公式是合适的。虽然本方法与三维源汇方法的计算结果横摇和纵摇的计算结果有一定误差,但比三维源汇方法剖分单元简单,计算的单元数少,同时也大大减少了计算时间,所以对于这一误差在工程实际中是可以接受的。
[1]Faltinsen O M,Michelsen F C.Motions of large structure in waves at zero Froude number[C]//In International Symposium on the Dynamics of Marine Vehicles and Structures in Waves.London,1974:91-106.
[2]戴遗山,贺五洲.简单Green函数法求解三维水动力系数[J].中国造船,1986(2):3-17.
[3]刘应中,缪国平.船舶在波浪上的运动理论[M].上海:上海交通大学出版社,1987:133-150.
[4]戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.
[5]Lean G H,Bowers E C,Spencer J M A.Quayship:A computer model of a ship against a quay in the presence of waves[M]. Oxon:HR Wallingford,1990.
[6]黄明汉,邹志利.波浪中多船多墩柱受力和运动的快速计算方法[J].船舶力学,2010,14(11):1227-1240. Huang Minghan,Zou Zhili.A simple and efficient calculating method for multiple ships and piers in waves[J].Journal of Mechanics,2010,14(11):1227-1240.
[7]Huang Minghan,Zou Zhili.A simple and efficient method for the coupled motions of multiple bodies[J].Journal of Ship Mechanics,2012,16(6):617-631.
A simple and efficient method for the fat ship in waves
HUANG Ming-han1,2,3,ZOU Zhi-li3,ZHANG Wen-zhong1,ZHANG Qing-he2
(1 CCCC-Key Hydrodynamic Laboratory for Coastal Engineering,Tianjin Port Engineering Institute Ltd.of CCCC. Tianjin 300222,China;2 School of Civil Engineering,Tianjin University,Tianjin 300072,China;3 State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)
This paper presents a simple and efficient calculation method for the ship motions in waves.The method is suitable for the slender ship and the fat ship to consider the three-dimensional flow field around the ship.The starting point of method is approximating the ship section by a rectangle with the same area as that of the original ship section.Then,the flow field is divided into inner domain below the ship bottom and the outer domain beside ship hull.The velocity potential in inner domain is given by an analytic solution,the velocity potential in outer domain is expressed by a source-sink distribution along the contour of ship water area.The two potential solutions are matched at the interface of two domains.This method is validated using the results for the three-dimensional source-sink distribution method.
wave forces;ship motions;fat ship;three-dimensional source-sink distribution method
U662.2
A
10.3969/j.issn.1007-7294.2014.07.004
1007-7294(2014)07-0760-11
2014-03-10
大连理工大学海岸和近海工程国家重点实验室开放课题基金资助项目(LP1409)
黄明汉(1981-),男,博士,工程师,E-mail:huangminghan@tpei.com.cn;
邹志利(1958-),男,大连理工大学教授,博士生导师,E-mail:zlzou@dlut.edu.cn。

