3-RPS型并联机构运动正解的研究①
任文博, 颜兵兵, 殷宝麟, 帅俊峰
(佳木斯大学机械工程学院,黑龙江佳木斯 154007)
0 引言
并联机构(Parallel Mechanism,简称 PM)[1~3],可以定义为动平台和定平台通过至少两个独立的运动链相连接,机构具有两个或两个以上自由度,且以并联方式驱动的一种闭环机构.与串联机器人相比具有无累积误差、负载力大、工作空间小,并且结构简单,动态响应好等特点[4~6],而被学者广泛研究.
机构的运动学分析包括两种问题,即运动学正解和运动学反解.运动学正解(即已知输入杆长参数求出运动平台的位置和姿态)是解决机构速度、加速度以及其他的受力分析、工作空间分析和机构综合等问题的基础[3,4],而运动学正解却包含非线性方程组而十分复杂.求解正解通常采用解析法和数值法,数值法多采用Newton-Raphson法、杆长修正法、同伦连续法等等[7~9],但是这种方法不一定能得到运动学正解的全部解,而且对初值的要求较高,解析法包括矢量代数法、几何法、矩阵法、对偶矩阵法、螺旋代数法、四元素代数法等等[10~12].
本文对3-RPS型并联机构进行运动学正解应用几何解析法进行了求解,得到全部的位置解,并给出对应空间图形,验证实数解的正确性.
1 建立坐标系及约束方程
3-RPS型并联机构如图1所示,由三条结构相同的运动支链连接运动平台与基座.其中第i运动支链(i=1,2,3)与基座Bi点处通过转动副Ri连接,与运动平台Mi点处通过球面副Si连接,Ri与Si间通过主动移动副Pi连接.设定基座坐标系OB-xByBzB,其中OB位于基座形状中心,xB轴、yB轴处于基座平面内.设定基座坐标系OM-xMyMzM,其中OM位于基座形状中心,xM轴、yM轴处于运动平台平面内.设定OBBi与xB轴夹角为φBi,且Ri的轴线与 OBBi垂直,OMMi与 xM轴夹角为 φMi..
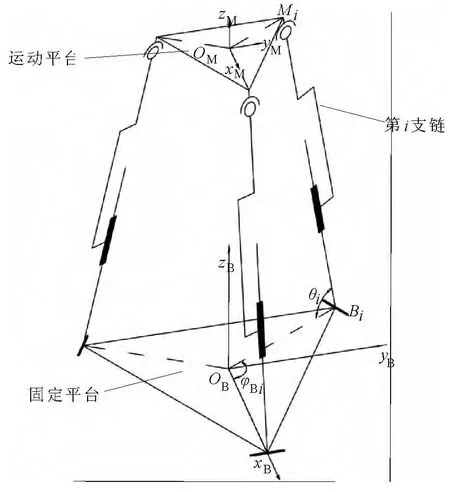
图1 3-RPS型并联机构
若基座半径为RB,运动平台半径为RM,设定BiMi=li,BiMi与 OBBi间夹角为 θi,则 Bi点在 OB-xByBzB中的坐标可表示为
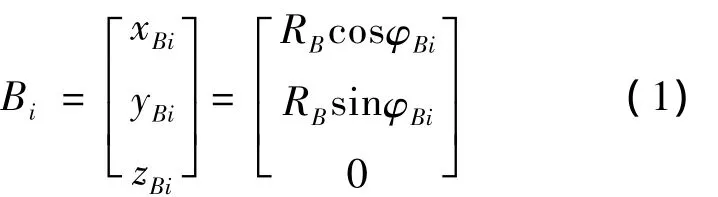
Mi点在OB-xByBzB中的坐标可表示为
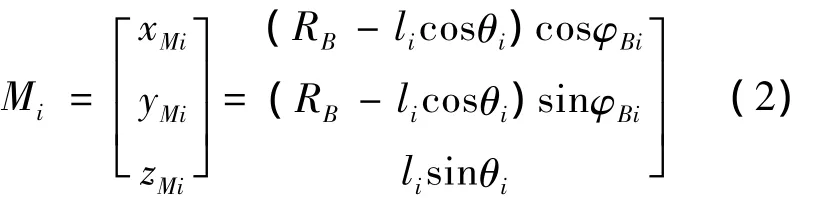
由于几何封闭关系可知,MjMk任意两点间距离不变,其中下标(j,k)=(1,2),(2,3),(1,3),即
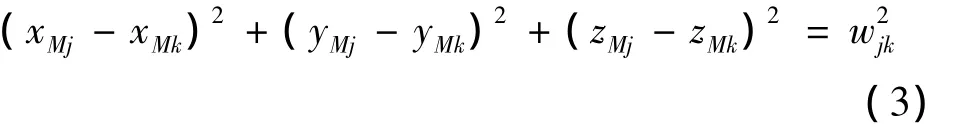
式中wjk为BjBk任意两点间距离可表示为
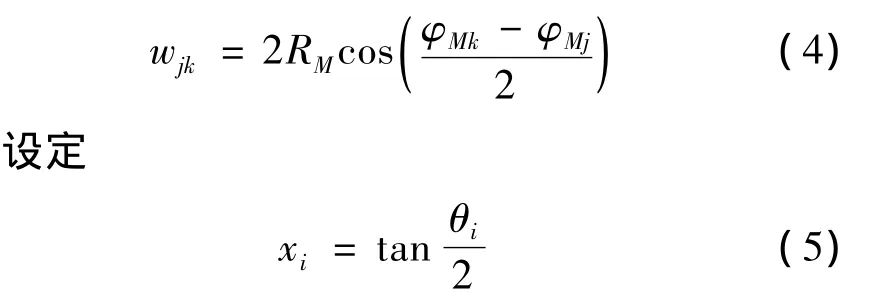

式(6)中的各项系数分别为
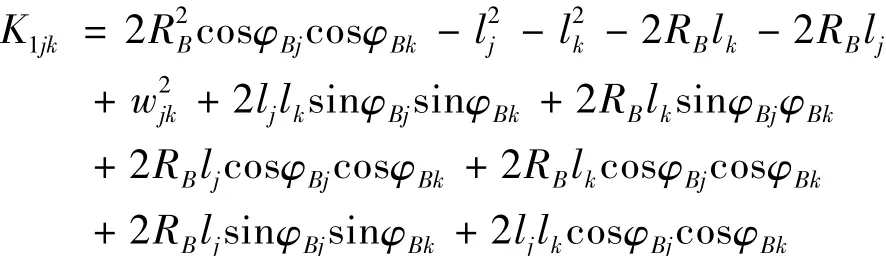

通过解方程组(6)可求得x1,x2,x3的符号解,将结果代入式(5)得θ1,θ2和θ3,进一步代入式(2)可求得动平台上各球铰在固定坐标系的坐标以及动坐标系的回转变换矩阵.
2 数值实例
若3-RPS型并联机构的结构参数如下:RB=0.1m,RM=0.05m,l1=0.24m,l2=0.18m,l3=0.2m,φBi= φMi=(i-1).将已知量带入方程(5),求得16组解,其中12组实数解,4组复数解,所得结果如表1.
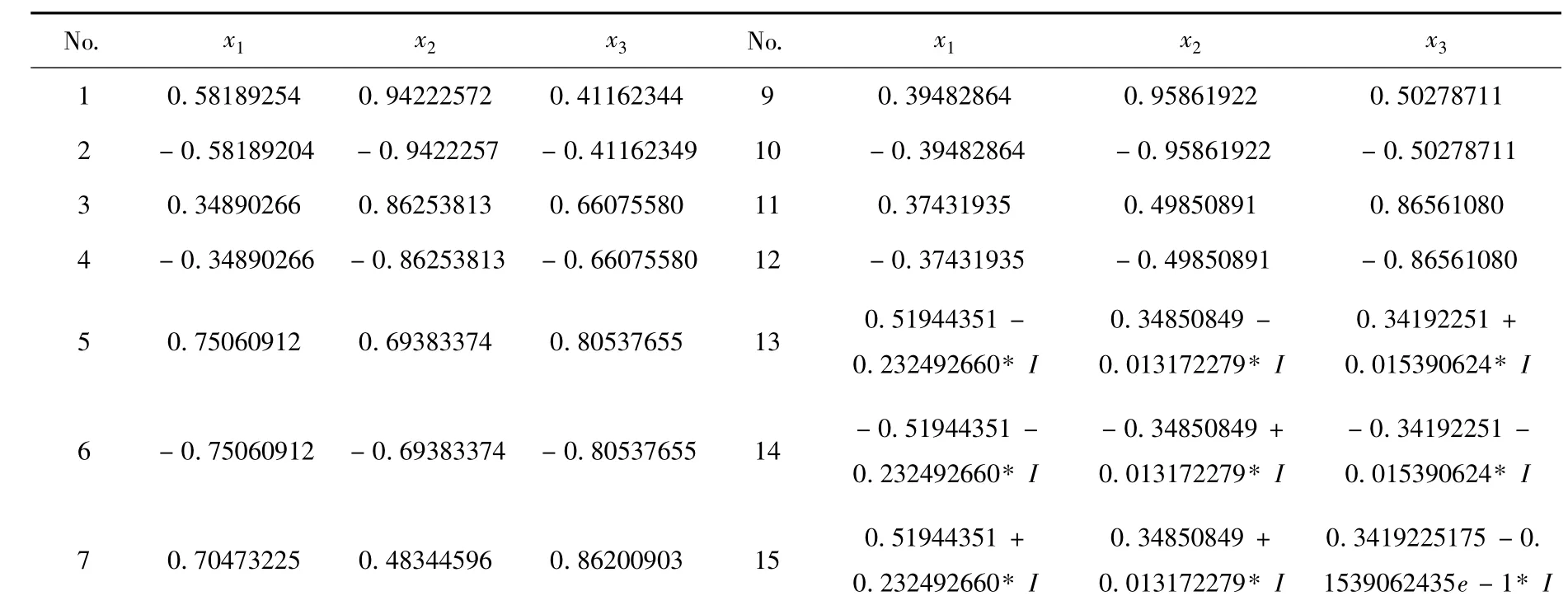
表1 非线性方程组的全部解
表2给出了其中12组实数解对应的机构第i运动支链与OBBi间的夹角θi.
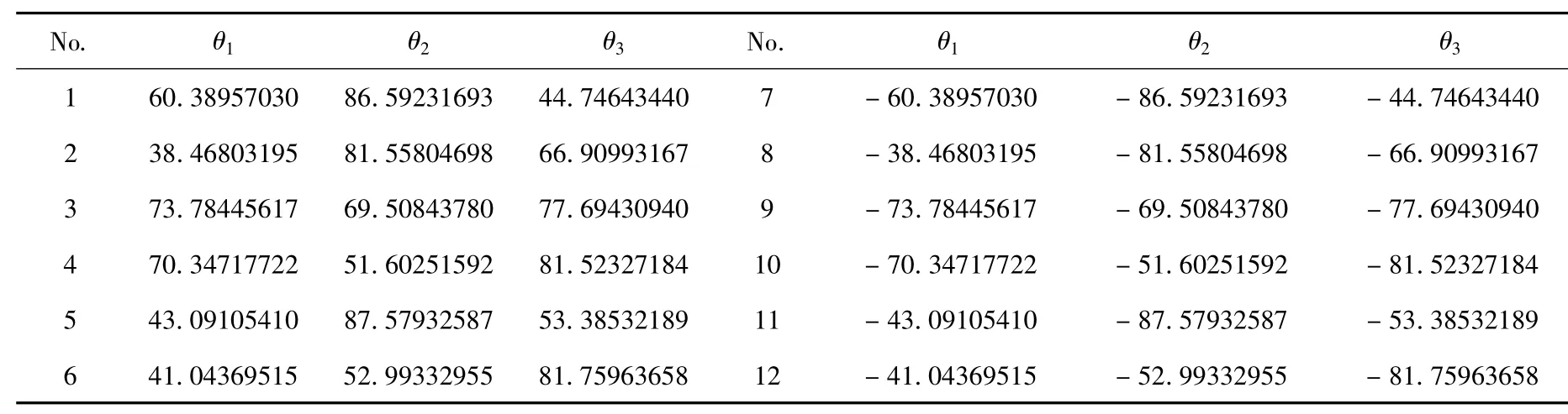
表2 并联机构运动学正解实数解(度)
由表1,表2可知16组解中有12组实数解,对应于其中的6组解的运动平台位于固定的上方,而对应于另外的6组解的运动平台位于固定平台的下方.前6组实数解对应空间图形,如图2(a)至(f)所示.
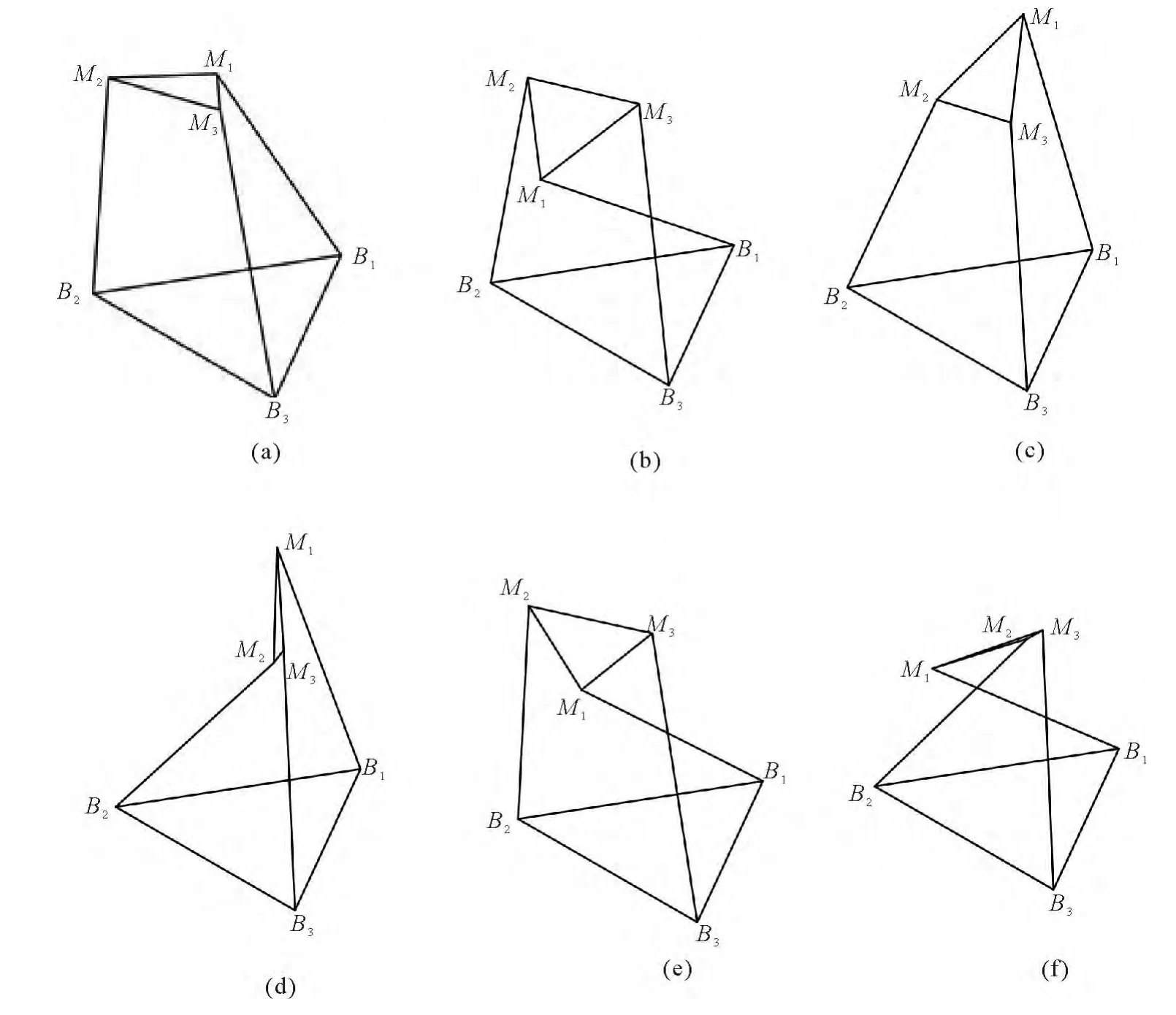
图2 部分实数解对应的机构空间图形
3 结论
由几何封闭关系建立了3-RPS型并联机构运动学正解方程,对所建立的非线性方程组进行了求解,获得运动学正解方程全部16组解,其中实数解12组,复数解4组,并针对所求得的部分实数解进行了空间图形验证.结果表明,针对3-RPS型并联机构所建立的运动学正解方程组求解方法精确、可靠.
[1]Murthy V,Waldron K J.Position Kinematics of the Generalized Lobster Arm and Its Series- Parallel Dual[J].Journal of Mechanical Design,1992,114:406.
[2]Stewart D A.Platform with 6- DOE Proc[J].On Institution of Mechanical Engineering.1965,18(1):371-386.
[3]Bo.nev I.The Tme Origins of Parallel Robots[J].The Parallel Mechanisms Information Center.2002.
[4]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社.2006.
[5]黄真,丁华锋.机构的结构类型综合综述[J].燕山大学学报,2003,27(3):189-191.
[6]刘宏伟,马质璞.3-PRS并联机构运动分析及仿真[J].机械设计与制造,2012,(1):211-215.
[7]韩先国,陈五一,陈鼎昌.基于路径跟踪原理求解6-SPS并联机构位置正解[J].北京航空航天大学学报,2002(6):370-372.
[8]李树军,王阴,王晓光.3-RPS并联机器人机构位置正解的杆长逼近法[J].东北大学学报(自然科学版),2001,22(3):285-287.
[9]韩方元,赵丁选,李天宇.3-RPS并联机构正解快速数值算法[J].农业机械学报,2011,42(4):229-233.
[10]刘宏伟,马质璞.3-PRS并联机构运动分析及仿真[J].机械设计与制造,2012,(1):211-215.
[11]Warldron K J,Raghavan M,Roth B.Kinematics of a Hybrid Series- Parallel Manipulation System[J].ASME Journal of Dynamic Systems,Measurement and Control,1989,111(2):211-221.
[12]Hashimoto Minoru,Imamura Yuichi.Kinematic Analysis and Design of a 3 DOF Parallel Mechanism for a Passive Compliant Wrist of Manipulators[J].Transactions of the Japan Society of Mechanical Engineers,1998,C64:2 116-2123.
[13]Pfreundschun G H,KhmerV,ThomasG S.Design and Control of a 3 DOF In- parallel Actuated Manipulator[C].Proceedings of IEEE International Conference on Robotics and Automation,1991,2:1 659-1664.

