均质土体中部分埋入桩纵向振动响应研究①
张智卿, 秦锐夫
(浙江树人大学城建学院,浙江杭州 310015)
0 引言
桩基纵向振动理论是桩基抗震、防震设计,动力机器基础设计和动力试桩的理论基础.近几十年来,学者们以桩周土体力学模型的建立为切入点,采用各种理论方法研究了动态竖向荷载作用下桩基的振动特性.王奎华[1]采用广义Voigt模型模拟桩周土体,研究了粘弹性桩的纵向振动性状.Militano[2]利用平面土模型,在时域内研究了瞬态扭转和纵向荷载作用下单桩的动力响应问题.阙仁波等[3],郑长杰等[4]基于连续介质模型模拟桩周土体,分别研究了实心桩和管桩的纵向振动问题.余俊等[5],王小岗[6]将桩土体视为饱和多孔介质,分别研究了饱和地基以及横观各向同性饱和地基中桩的纵向振动特性.然而,以上研究问题的主要对象为完全埋入式桩基.
值得注意的是,上述研究问题的主要对象为完全埋入式桩基.然而,部分埋入式桩基已在道路,桥梁和近海平台等大型工程中得到了广泛的应用,关于该问题的研究目前主要集中在部分埋入单桩的自由振动特性和群桩纵向振动特性.李炳求等[7]采用特征值搜索法得出部分埋入单桩的自振频率和振型.钟锐等[8]在考虑土体非线性的前提下,研究了部分埋入群桩的纵向振动特性.
迄今为止,关于部分埋入桩完整性分析方面的研究仍相对不足.余云燕等[9]基于回传射线矩阵法,研究了部分埋入变模量桩的动力响应问题.然而,该研究采用的弹簧和阻尼参数难以直接与工程实际参数相匹配.因此,本文基于单相土体的运动方程,采用解析的方法研究均质土体中部分埋入桩的纵向振动响应问题.
1 基本假设及定解问题
计算模型如图1所示,桩身沿着垂直方向分为完全埋入地基土体的桩段1和未埋入地基土体的桩段2.为了建立适合该问题的数学模型,现假设如下:(1)桩段1周围土体为均质、各向同性线性粘弹性体,其材料阻尼采用滞回阻尼形式;,地基土层上表面为自由边界;(2)桩为弹性、垂直、圆形均匀截面桩,桩身底部为弹性边界,桩与周围土体完全连续接触;(3)桩土系统初始处于静止状态.
忽略土体纵向位移沿深度方向梯度时,土体在瞬态纵向激励力作用下的控制方程可以表示为:
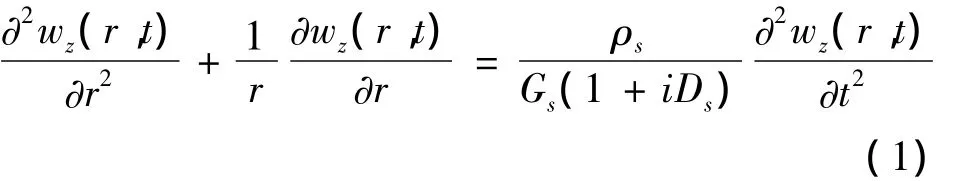
式中:wz(r,t)表示土体纵向振动位移;Gs,Ds和 ρs分别表示土体的剪切模量,阻尼系数和密度.
由于桩土体系初始为静止状态,对式(1)进行拉普拉斯变换可得:
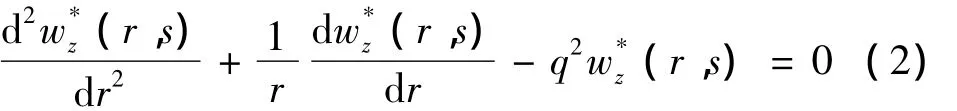
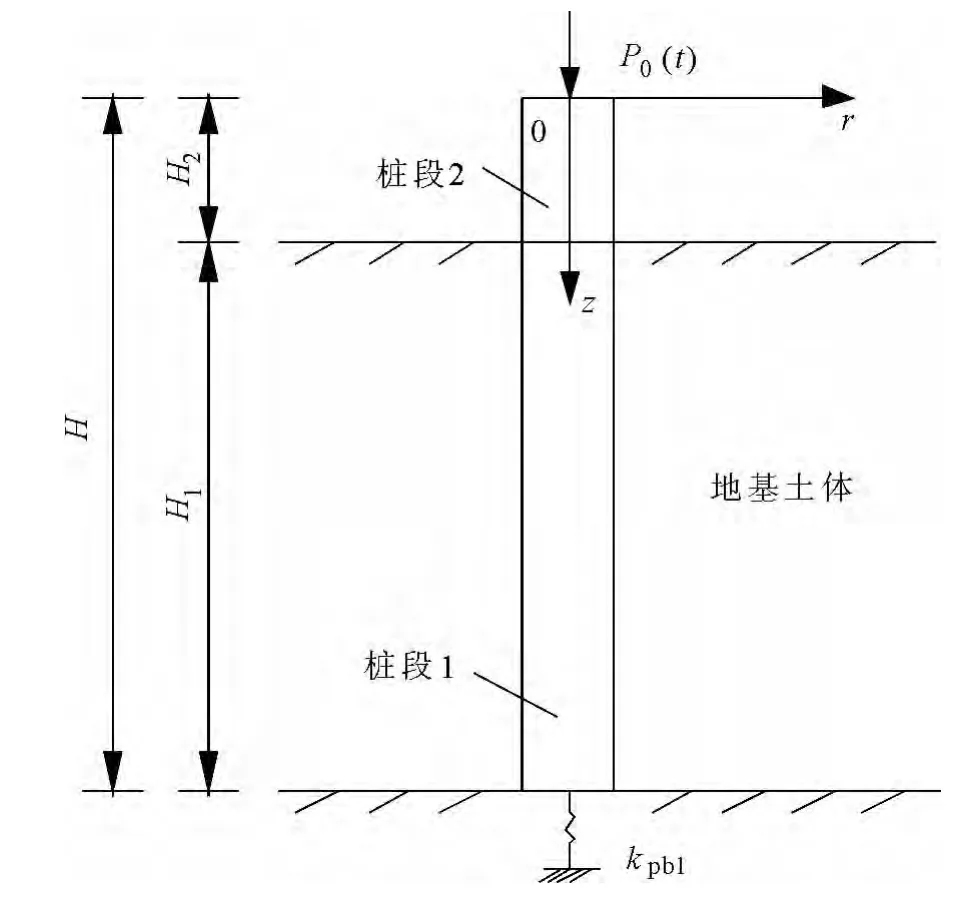
图1 桩土动力相互作用示意图
鉴于桩土系统初始静止,经过拉普拉斯变换后桩段1和桩段2动力平衡方程可以分别表示为:

式中:Ep,ρp和r0分别表示桩的弹性模量,质量密度和半径分别表示拉氏变换后桩段1和2的纵向位移表示拉氏变换后桩周土体作用在桩身的侧壁切应力.
桩段1拉氏变换后的边界条件可以写为(采用局部坐标表示):

桩段2拉氏变换后的边界条件(采用局部坐标表示):

式中:H2表示桩段2的长度;kpb2表示桩段1顶部作用于桩段2底部的支撑系数;P*0(s)表示拉氏变换后作用于桩顶的竖向力.
桩土接触面两侧的衔接条件:

2 部分埋入桩纵向振动问题求解
2.1 土体纵向振动解
方程(2)解的可以表示为:
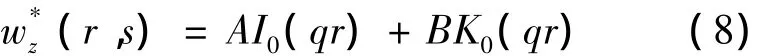
式中:I1(qr)和K1(qr)分别为一阶第一类和第二类修正的贝塞尔函数.由土层无限远处土体的应力和位移衰减为零,可得A=0,则方程(8)可以进一步表示为:

桩土接触面处的侧壁切应力可以表示为:
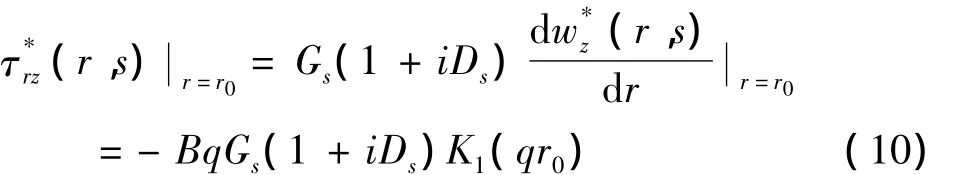
2.2 桩纵向振动问题求解
利用桩土接触面的位移衔接条件式(7),将式(9)和(10)代入式(3)中,可得:

方程(11)的解可以表示为:
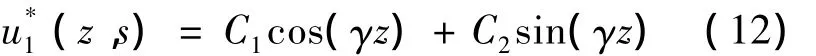
式中:

将式(12)代入边界条件(5)中可以得到C1和C2,则桩段1顶部阻抗函数可以进一步表示为:
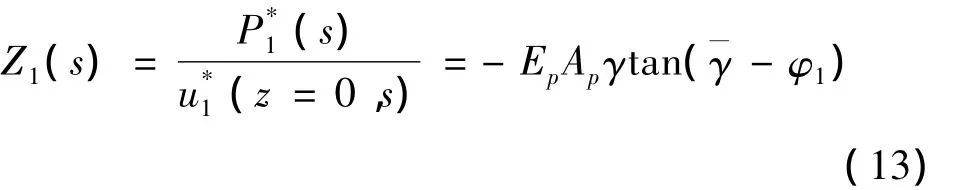
方程(4)的解可以表示为:

式中:κ =(- ρps2/Ep)1/2
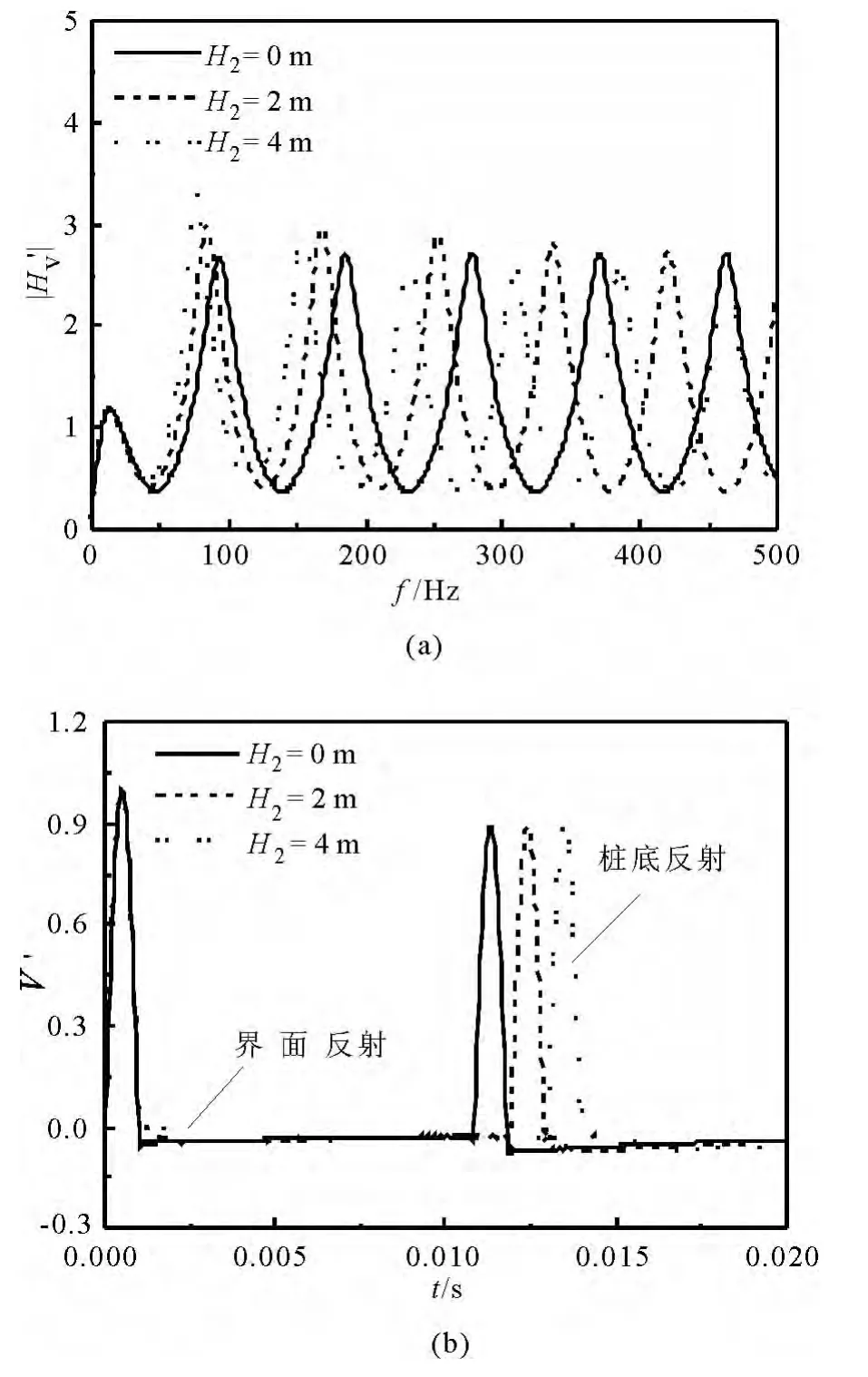
图2 桩段2长度变化对桩顶速度导纳和速度时域响应影响(H1=20m,Gs=21×07Pa)
根据阻抗函数递推原理,桩段1顶部阻抗与桩段2底部支撑系数相等,即kpb2=Z1(s).然后,将式(14)带入边界条件式(6)可以得到D1和D2,则桩顶阻抗函数可以进一步表示为:
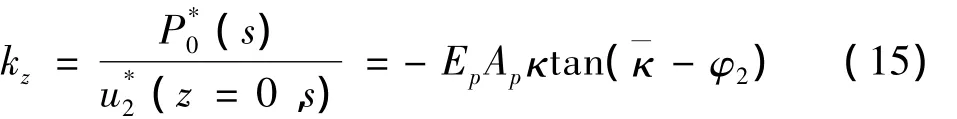
令s=iω,可以在频域内得到桩顶速度响应函数(或称为桩顶速度导纳):


式中:θ= ωTc,t=t/Tc和T=T0/Tc分别表示无量纲频率,时间和脉冲宽度;Tc=H/Vp表示弹性纵波从桩顶传递到桩底经历的时间.
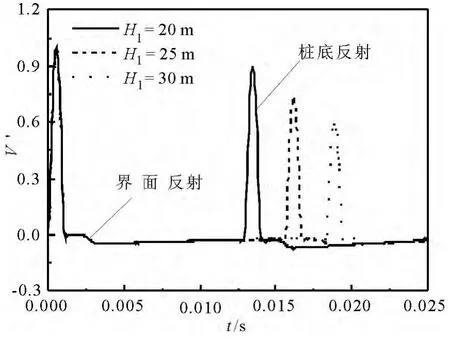
图3 桩段1长度变化对桩顶速度时域响应影响(H2=4m,Gs=2×107Pa)
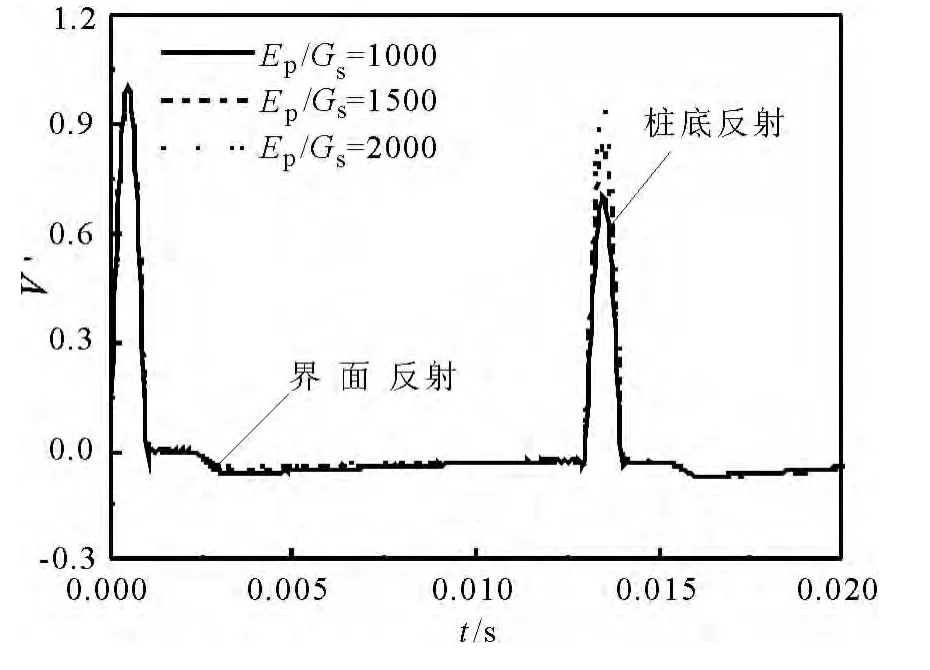
图4 桩土模量比变化对桩顶速度时域响应影响(H1=20m,H2=4m)
3 数值计算与讨论
下面将通过数值计算研究主要参数对桩顶速度导纳和速度时域响应的影响,土体及桩的常用参数取为:ρs=1600kg/m3,r0=1.0m,ρp=2500kg/m3,Vp=3700m/s,μ =0.25,Ds=0.02,kpb1=4Gsr0/(1- μ).
桩段2长度变化对桩顶速度导纳和速度时域响应的影响如图2所示.由图2(a)可见,当H2为0(即完全埋入桩)时,速度导纳曲线上除第1阶共振峰外,以后各阶共振峰幅值相等;随着H2的增大,各阶共振频率逐渐减小,存在大峰夹小峰的现象,这与缺陷桩响应曲线类似,表明速度导纳曲线无法应用于部分埋入桩的完整性分析之中,因此下文中将不再研究部分埋入桩的速度导纳响应变化特征.由图2(b)可以看出,部分埋入桩桩段分界面处存在着一定程度的界面反射信号,且该信号不存在2次反射现象.随着H2的增大,由于纵波传播距离的增大,界面和桩底反射信号对应的时间也相应延后,而桩底反射信号幅值基本上未发生改变,这表明入射脉冲能量在上部桩段耗散地很少.
图3反映了桩段1长度变化对桩顶速度时域响应的影响.由图3可见,桩段分界面处的反射信号与H1大小无关,而随着H1的增大,入射脉冲在下部桩土体系中产生了更多的耗散,导致桩底反射信号的幅值逐渐减小.
图4反映了固定桩身弹性模量时,桩土模量比变化对桩顶速度时域响应的影响.由图4可见,随着桩土模量比大范围地增大(即土体剪切模量减小),桩段分界面处的反射信号的幅值有着略微的减小,因此在实际工程中可以不考虑土体性质变化对界面反射信号的影响.此外,随着桩土模量比的增大,桩底反射信号幅值有着明显地增大,这与完全埋入桩的变化规律相同.
4 结论
(1)桩段2长度对桩顶速度导纳响应有着明显的影响,随着的增大,导纳曲线的变化规律与缺陷桩响应曲线类似,因此速度导纳曲线无法应用于部分埋入桩的完整性分析之中.
(2)随着桩段2长度的增大,桩段界面和桩底反射信号对应的时间相应延后,桩底反射信号幅值基本上未发生改变.桩段1长度变化与桩段分界面处的反射信号无关,且随着H1的增大,桩底反射信号的幅值逐渐减小.
(3)部分埋入桩桩段分界面处存在着一定程度的界面反射信号,该信号不存在2次反射现象,且受到桩周土体性质变化的影响很小.因此,在实际工程中可以忽略土体性质变化对界面反射信号的影响,同时需要注意防止此类信号作为缺陷信号的误判.
(4)桩土模量比变化对桩底反射信号幅值的影响与完全埋入桩的变化规律一致,随着桩土模量比的增大,桩底反射信号幅值有着明显地增大.
[1]王奎华.成层广义Voigt地基中粘弹性桩纵向振动分析与应用[J].浙江大学学报(工学版),2002,36(5):565-571.
[2]G.Militano,R.K.N.D.Rajapakse.Dynamic Response of a Pile in a Multi-layered Soil to Transient Torsional and Axial Loading[J].Geotechnique,1999,49(1):91- 109.
[3]阙仁波,王奎华,祝春林.考虑土体轴对称波动时变模量桩的纵向振动特性[J].振动工程学报,2010,23(1):94-100.
[4]郑长杰,丁选明,刘汉龙,等.考虑土体三维波动效应的现浇大直径管桩纵向振动响应解析解[J].岩土工程学报,2013,35(12):2247-2254.
[5]余俊,尚守平,任慧,等.饱和土中桩竖向振动响应分析[J].工程力学,2008,25(10):187-193.
[6]王小岗.层状横观各向同性饱和地基中桩基的纵向耦合振动[J].土木工程学报,2011,44(6):87-97.
[7]李炳求,郑镇燮,李光范,等.部分埋入弹性地基的变截面桩自由振动[J].岩土工程学报,1999,21(5):609-613.
[8]钟锐,黄茂松,任青,等.考虑土体非线性的部分埋入群桩竖向振动分析[J].同济大学学报(自然科学版),2011,39(12):1760-1766.
[9]余云燕,余莉芬.均质土中部分埋入变模量桩的波动响应研究[J].振动工程学报,2010,23(2):200-205.

