箍筋约束高强混凝土轴压力学性能试验研究①
魏公涛
(同济大学建筑工程系,上海 200092)
0 引言
从1903年considere发现螺旋箍筋可以有效约束混凝土开始,箍筋约束混凝土的研究已有一百多年的历史.1929年 Richart[1]根据螺旋箍筋约束圆柱体试件的试验结果提出了箍筋约束对峰值强度的影响公式,其后 kent&Park[2]、Sargin[3]等人纷纷进行了试验研究并提出了箍筋约束效应的经验模型;20 世纪 80 年代,Sheikh[4]、Mander[5]等人提出有效约束系数来考虑有效约束面积,从而统一了不同配箍形式和截面形式的影响;80年代中期以后,Yong[6]、Cusson[7]和 Saatcioglu[8]等人对于箍筋约束高强混凝土进行了研究,并提出了一些模型.国内的研究始于20世纪80年代,张秀琴、过镇海[9]等人进行了相关试验,并提出了约束模型;90年代后期以后,关萍[10]、史庆轩[11]等人对于高强混凝土的箍筋约束进行试验和理论研究.通过诸多的研究,箍筋约束可以明显的提高混凝土的轴压力学性能,包括峰值强度和延性,尤其对于下降段延性较差的高强混凝土,采用箍筋约束来提高其延性具有重要的意义.
随着对于混凝土材料及结构的研究,一方面,混凝土材料及结构的非线性被越来越深入的认识,并且随着有限元理论和计算机技术的发展,复杂结构的非线性分析成为现实,从而实现了对混凝土材料更充分的利用;另一方面,随着结构分析越来越精细化和材料性能的充分利用,随机性的影响体现的越来越明显,深入认识混凝土材料的随机性及其在结构力学分析中的涨落对于充分利用混凝土强度和合理设计结构有着深远的影响.
1 试验概况
本试验旨在研究箍筋约束对于混凝土单轴受压力学性能的影响,包括对峰值强度和延性的提高以及对应力应变全曲线随机性的影响.试件截面为150mm*150mm,高度为400mm,箍筋内侧距试件外边缘为18mm,箍筋形式为普通方箍,直径为6mm,强度为HRB400,沿试件周边均匀配置8根纵筋,直径为12mm,强度为HRB335,试件截面示意图见图1.

图1 截面示意图
试件配箍情况列于表1.

表1 试件配箍表
备注:L,M,H:低、中、高配箍率试件,核心混凝土取为箍筋内侧部分.

图2 轴压试验照片
本试验在MTS815液压伺服试验机上进行,试验照片及压坏试件照片分别见图2和(a)高配箍率试件(b)中等配箍率试件(c)素混凝土试件

图3 试件压坏照片
图3,试验中素混凝土试件在出现裂缝后突然破坏,承载力迅速降低,一条斜向主裂缝几乎贯通整个试件,见图3(c),而配箍试件则会在箍筋的约束下承载力逐渐下降,最后出现较明显剪切变形,见图3(a)(b).试验中配箍试件会出现两个承载峰值,第一个峰值达到后保护层开始出现裂缝、剥落,此部分混凝土承载力迅速降低导致整个试件承载力下降,此时核心混凝土在箍筋约束下承载力依旧在上升,出现第二个承载峰值,此时核心混凝土承载力亦达到峰值.从试验现象来看,箍筋约束,即使是约束效率最低的普通方箍,对于后续延性的提高也很明显.试验后期部分箍筋被拉断,纵筋被压屈,见图4.

图4 破坏试件细部照片
2 试验结果及分析
2.1 核心混凝土应力应变全曲线计算方法
配箍试件由于配有箍筋,对于混凝土有约束作用,故可以得到完整的全曲线.试件应变见下式:
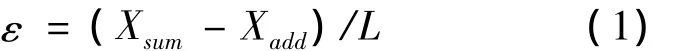
其中,Xsum为试验机总位移,Xadd为试验机附加位移,L为试件高度,均为400mm高.
核心混凝土应力计算见下式:
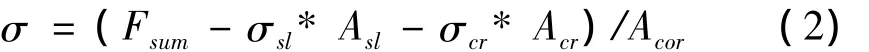
其中,Fsum为试件承受的总荷载,σsl,Asl为分别为纵筋应力和纵筋总面积,σcr,Acr为分别为混凝土保护层应力和保护层面积,Acor为核心混凝土面积.
2.2 素混凝土试验结果
本试验测试了四个素混凝土试件的全曲线指标,四个素混凝土试件尺寸均为150*150*400,在MTS815液压伺服试验机上进行轴压,得到峰值强度和峰值点应变列于表2.
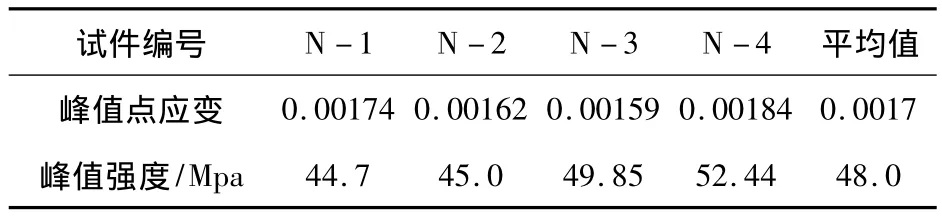
表2 素混凝土试验结果
将表2中参数均值代入全曲线方程中得到素混凝土全曲线参数,平均全曲线见图5.公式(3)中保护层采用此全曲线.
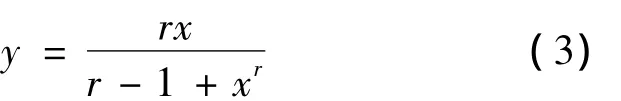
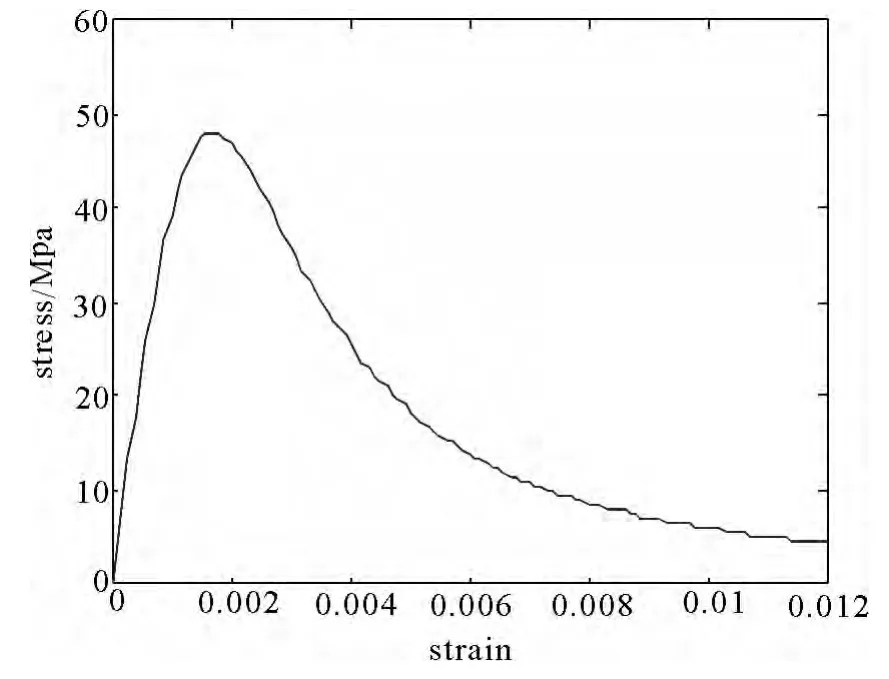
图5 素混凝土应力应变全曲线
2.3 低、中、高配箍率试件结果及分析
本试验得到5个低配箍率试件结果,5个中配箍率试件结果,7个高配箍率试件结果,根据2.1节中的公式得到核心混凝土全曲线见图6.
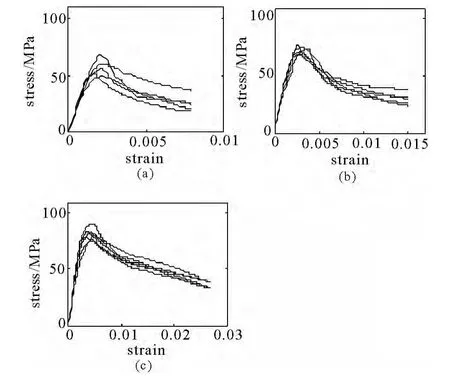
图6 约束混凝土试验全曲线
求得平均全曲线见图7,并将全曲线关键参数的约束影响结果示于表3和图8.
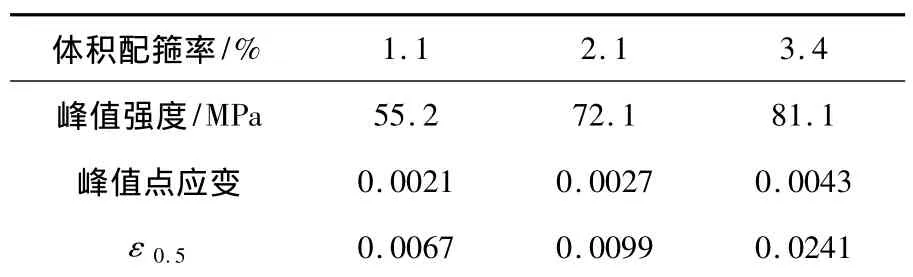
表3 箍筋约束对于全曲线关键参数影响表
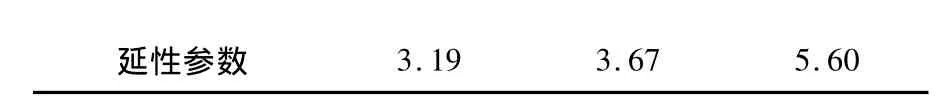
注:ε0.5:下降段降到50% 峰值强度时对应的应变;延性参数表达式为 ε0.5/εcc.
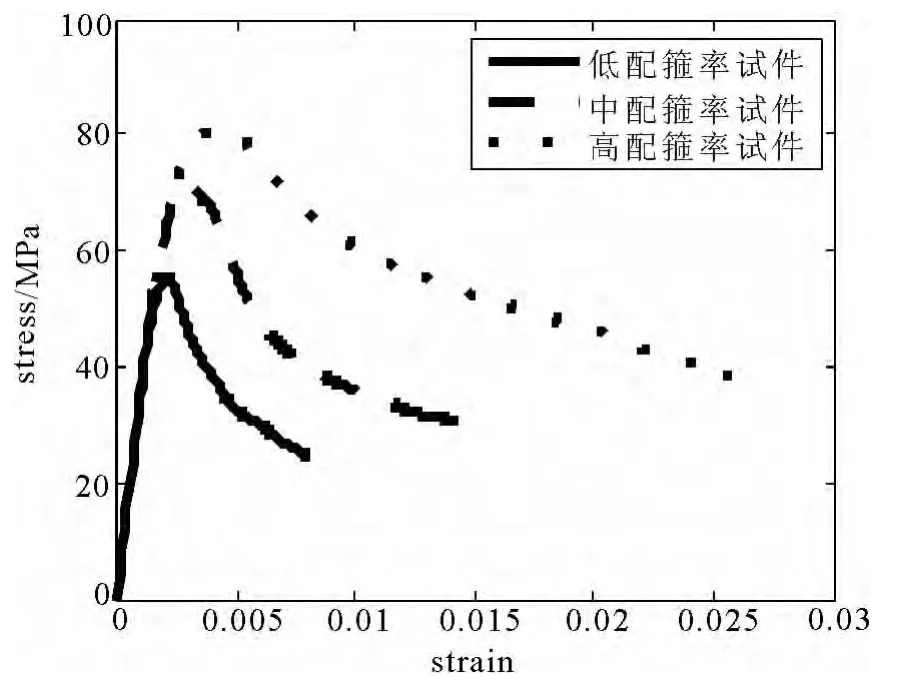
图7 不同配箍率试件全曲线
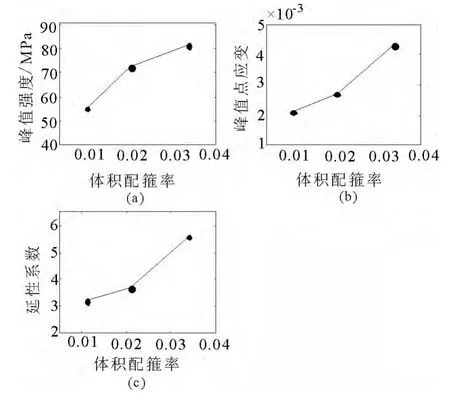
图8 全曲线关键参数受约束影响趋势图
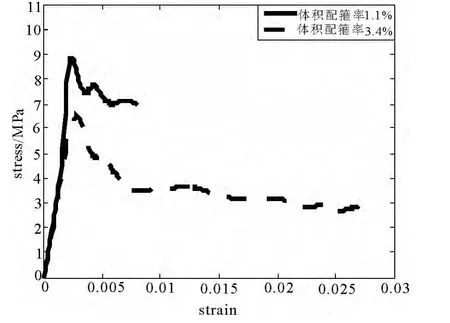
图9 应力标准差-应变图
得到试验结果的应力标准差-应变曲线见图9.
从图7、表3和图8中可以明显看到,箍筋约束对于高强混凝土力学性能的提高非常明显,当配箍率从1.1%提高到3.4%时,峰值强度提高了47%,延性提高了76%,这说明利用箍筋约束改善高强混凝土延性是可行的.
从图6中可以看出箍筋约束对于试验结果的离散性影响也十分明显,随着应变增大,离散性减小,说明随着箍筋约束变强,混凝土材料本身的随机性减小;从图9中看出,当配箍率从1.1%提高到3.4%时,其峰值从 8.95MPa 降低到 6.52Mpa,且后续段高配箍率试件的离散性明显小于低配箍率试件.从直观上分析,箍筋约束阻止了素混凝土试验中一出现微裂缝便迅速贯穿为较大裂缝的行为,使裂缝出现更为均匀,进而逐渐形成一条斜向的剪切带,这种延性破坏模式比脆性破坏模式随机性更小.
3 结论
(1)箍筋约束能明显的提升高强混凝土的力学性能,包括峰值强度和延性,而延性的提高对于高强混凝土而言具有重要意义.
(2)箍筋约束可以明显减小混凝土力学性能的随机性,全曲线下降段处在一个随约束增大而变窄的带状区域.
[1]F.E.Richart,A.Brandtzaegand R.L.Brown.The Failure of Plain and Spirally Reinforced Concrete in Compression[J].University of Illinois Engineering Experimental Station,Bulletin,NO.190,1929,74pp.
[2]D.C.Kent and R.Park.Flexural Members with Confined Concrete[J].Journal of Structural Division,1971,97(ST7):1969-1990.
[3]M.Sargin,S.K.Ghosh and V.K.Hander.Effects of Lateral Reinforcement upon Strength and Deformation of Concrete[J].Magazine of Concrete Research,1971,23(75-76):99-110.
[4]Sheikh S.A.,Uzumeri S.M.Analytical Model for Concrete Confinement in Tied Columns[J].Journal of Structural Division,ASCE,1982,108(ST102):2703-2722.
[5]Mander,Priestley M.J.N.and R.Park.Theoretical Stress-Strain Model for Confined Concrete[J].Journal of Structural engineering,1988,114(8):1804-1826.
[6]Yong Y.K.,Nour M.G.and Nawy E.G.Behavior of Laterally Confined High- Strength Concrete under Axial Loads[J].Struct.Engrg.,ASCE,1988,114(2):332- 351.
[7]Cusson D.and Paultre P..Stress- Strain Model for Confined High- Strength concrete[J].Struct.Engrg.,ASCE,1995,121(3):468– 477.
[8]Saatcioglu M.and Razvi S.R.Confinement Modelfor High-Strength Concete[J].J.Struct.Engin.,ASCE,1999,125(3):281-289.
[9]张秀琴,过镇海,王传志.反复荷载下箍筋约束混凝土的应力应变全曲线方程[J].工业建筑,1985,12:16-20.
[10]关萍,王清湘,赵国藩.高强约束混凝土应力-应变本构关系的试验研究[J].工业建筑,1997,27(11):26-29.
[11]史庆轩,杨坤,刘维亚,张兴虎,姜维山.高强箍筋约束高强混凝土轴心受压力学性能试验研究[J].工程力学,2012,29(1):141-149.

