某变曲率摩擦摆隔震支座设计与有限元分析①
徐 壮, 黄俊俊, 黄林根
(1.同济大学结构工程与防灾研究所,上海 200092;2.上海通亿橡塑制品有限公司,上海 201705;3.上海市政工程设计研究总院,上海 200092)
0 引言
Zayas等人[1]于1985年首次提出摩擦摆隔震支座.由于此种支座具有很好的自复位能力,摩擦摆隔震技术在桥梁工程中得到了广泛应用.传统的球面摩擦摆隔震支座由于其滑动曲面为球面,球摆在自复位运动过程中其曲率半径为一固定值,导致支座的隔震周期也为一确定常数.而在近断层常伴有长周期脉冲形地震波,这样容易与隔震结构发生低频共振[2].为克服这一缺陷,使支座的隔震周期随着球摆的水平滑动位移不断改变,避免共振现象的发生.有学者研制出变曲率摩擦摆隔震支座,将支座原有球形滑动曲面改进设计为变曲率滑动曲面,它的曲率半径在支座的整个水平滑动范围内并非定值.
2000年,Praneshl和Sinha研发出变频摆隔震支座(VFPI)[3,4],并将其与摩擦摆支座(FPB)和纯摩擦滑移隔震系统(FP)进行了对比研究,验证了它对减轻结构扭转耦合效应和近断层脉冲式地面运动下的结构响应是非常有效的[2].卢炼元等[5]探讨了支座高度和摩擦系数等参数对变曲率隔震支座隔震效果的影响,并进行了试验验证.目前对变曲率摩擦摆隔震支座只针对特定支座的定量试验研究,对不同参数对其耗能能力的影响规律及其自复位能力的定性研究尚不够全面.针对上述情况,本文分析了曲面函数方程不同参数变化对变曲率滑动曲面的影响.并将某特定球面摩擦摆支座改进为变曲率摩擦摆支座,对比了不同曲率变化程度的变曲率摩擦摆支座和球面摩擦摆支座在低周反复荷载作用下的滞回性能.
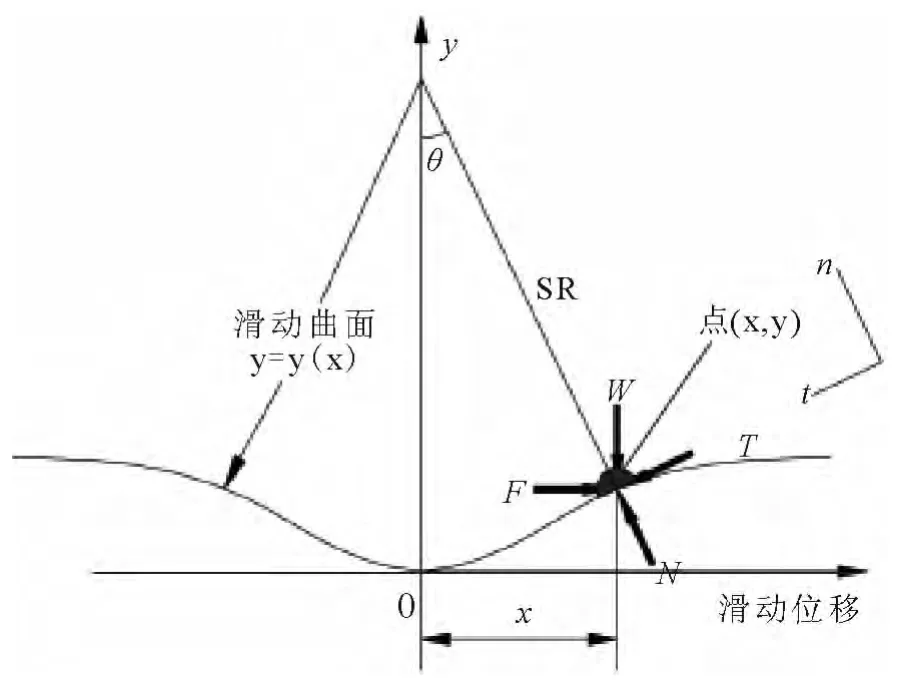
图1 支座滑动曲面示意图
1 变曲率滑动曲面方程及参数分析
支座滑动曲面示意图如图1所示,VFPI的滑动曲率半径是一个随支座球摆水平滑动位移变化的连续函数.其滑动面的曲面函数由椭圆方程转化而来,表示为[6]

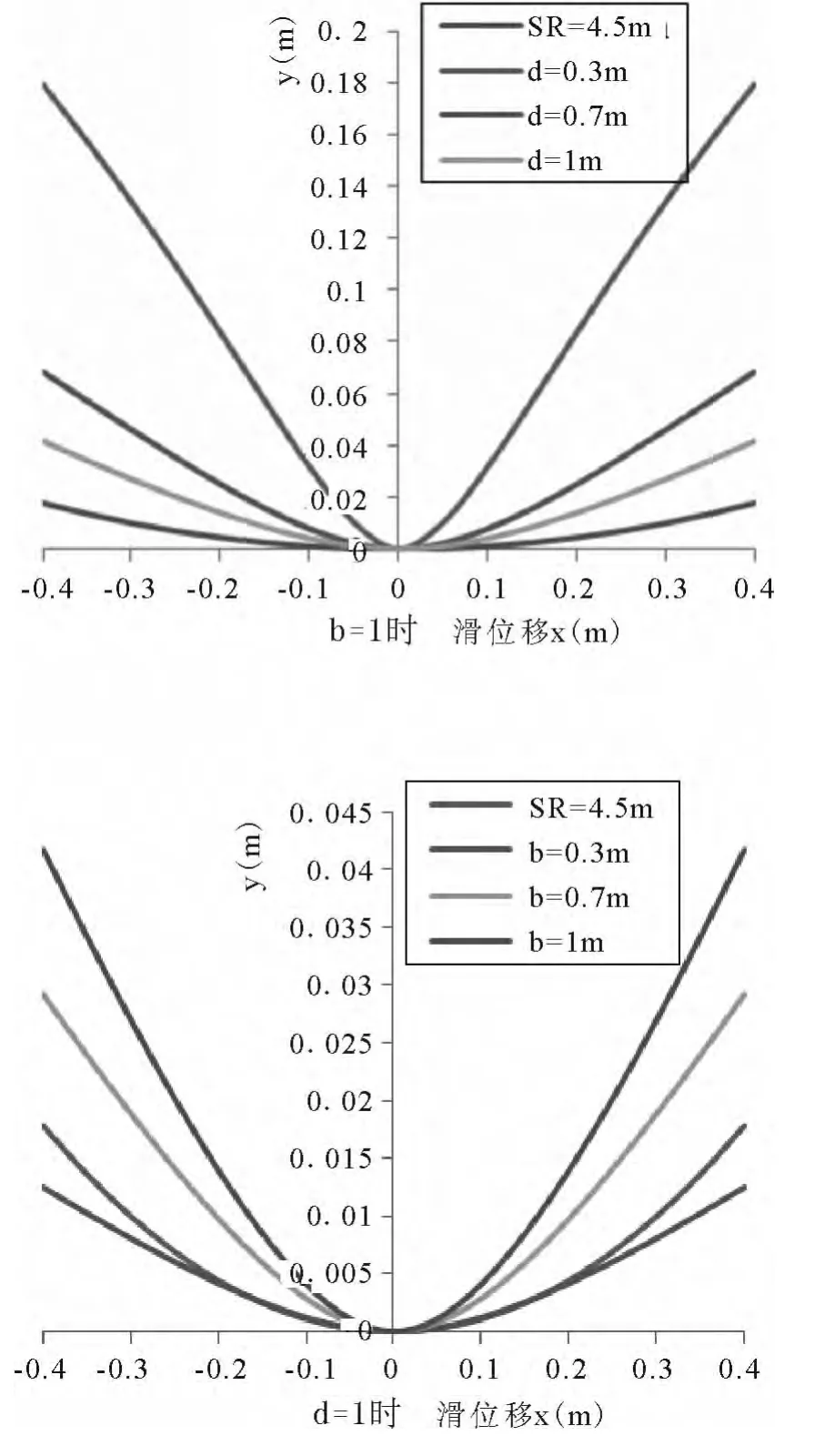
图2 VFPI曲面函数与球面函数对比图
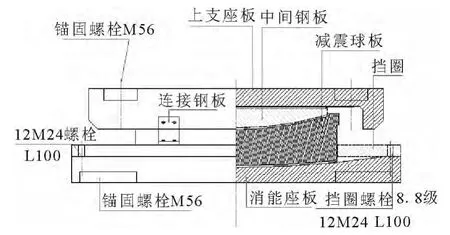
图3 球面摩擦摆隔震支座剖面图
式(1)中b,d是和支座水平滑动位移相关的常数.将式(1)曲线方程绕y轴旋转360°即形成滑动曲面.为了解曲面参数b,d变化时VFPI滑动曲面的变化情况,绘制了VFPI曲面函数和球面半径为4.5m的球面函数的对比图,如图2所示.由图2可知,b变小或d变大会使滑动曲面变化更平缓,更接近于球面.

图4 b,d参数变化时y(x)曲线图
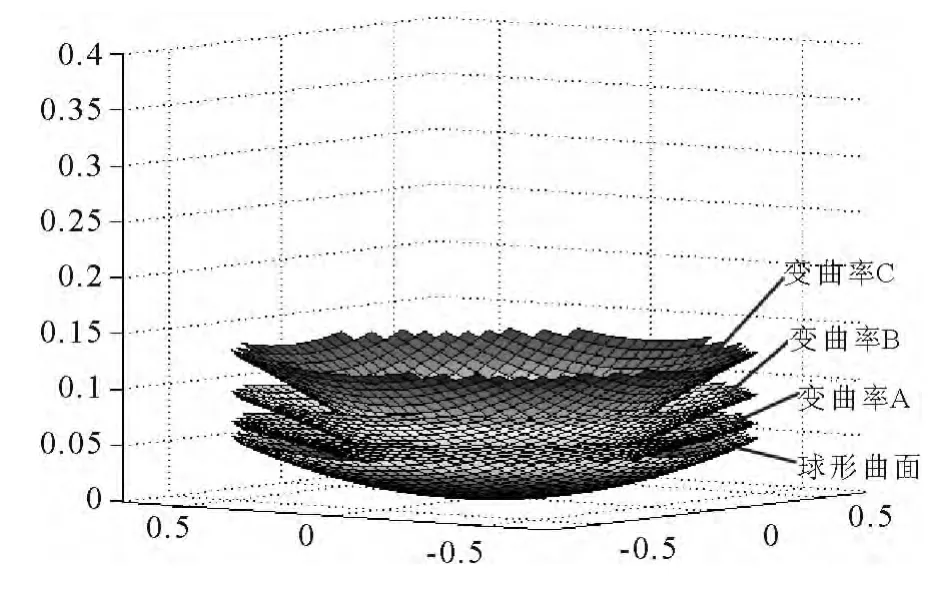
图5 三种变曲率滑动曲面与球形曲面的三维对比图

图6 变曲率摩擦摆隔震支座模型示意图
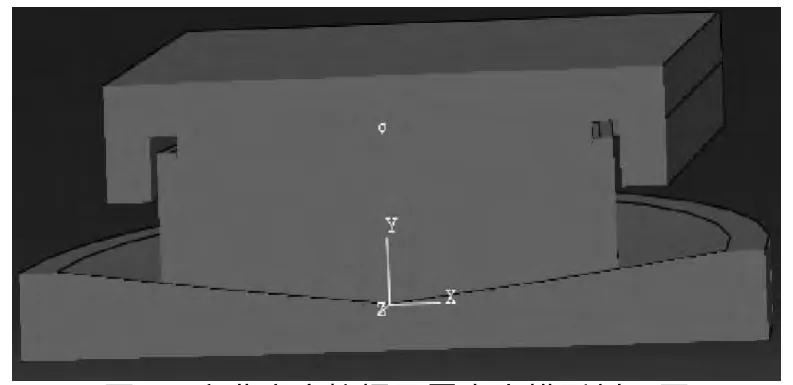
图7 变曲率摩擦摆隔震支座模型剖面图
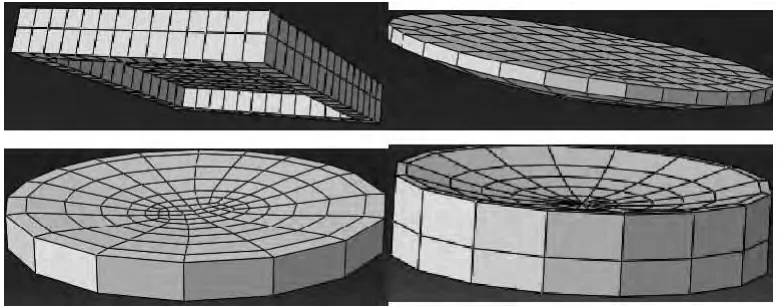
图8 采用C3D8I网格划分示意图
2 变曲率摩擦摆隔震支座设计
上海通亿橡塑制品有限公司生产了一种球面摩擦摆隔震支座,支座剖面图如图3所示.该支座的特点是当水平力远小于设计最大水平力时,限位螺栓和挡圈发挥作用,使球摆在消能座板内固定不动;当水平力接近甚至超过设计最大水平力时,限位螺栓依次被剪断,限位螺栓和挡圈失效,此后减震球摆在消能座板内来回摆动摩擦耗能.这样实现了摩擦摆支座在地震作用下的多道抗震防线作用.

图9 竖向荷载和水平位移加载时间历程
该球面摆支座的减震球摆和消能座板的滑动曲面均为半径为4.5m的球面,其水平滑动位移限值为0.2m,减震球摆、消能座板与聚乙烯板之间的摩擦系数为0.05.现将其改为变曲率摩擦摆隔震支座,即将滑动曲面为球面的减震球摆和消能座板改为变曲率滑动曲面.结合图1所示滑动曲面示意图,支座的曲率中心坐标为(0,4.5),假设滑动曲面任意一点到曲率中心的距离为 SR,则 SR=(m).当滑动曲面为球面,滑移量为 x=0.2 或-0.2m 时,y=0.00445m.现提出3种变曲率滑动曲面设计方案,要求当减震球摆的水平滑动位移达到设计的限值,即x=0.2 或-0.2m 时,y分别为 0.015m(变曲率A)、0.02m(变曲率 B)和0.03m(变曲率 C).
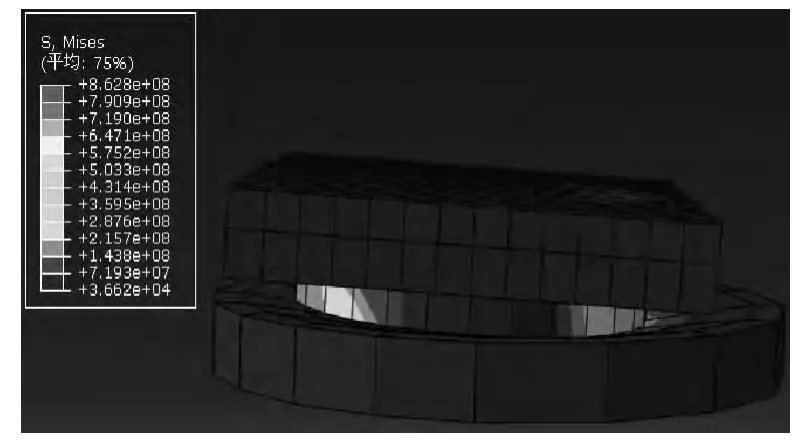
图10 支座水平滑移200mm时MISES应力云图
调整式(1)中的b,d值,可以实现上述3种方案的设计要求.现仅以变曲率B加以说明,如图4所示.从图4可以看出:当x=0.2或x=-0.2时,有3条曲线的y值在0.02附近,我们希望滑动曲面尽量接近于球面,这样可以节省支座的材料用量.经试算,当 b=0.5,d=0.5 时,式(1)变为

(2)上式中,当x=0.2或x=-0.2时,y=0.020843,接近0.02.因此式(2)即为该支座所求的变曲率滑动曲线方程,变曲率滑动曲面由式(2)方程绕y轴旋转360°而成.3种变曲率滑动曲面与球形曲面的三维对比图如图5所示.
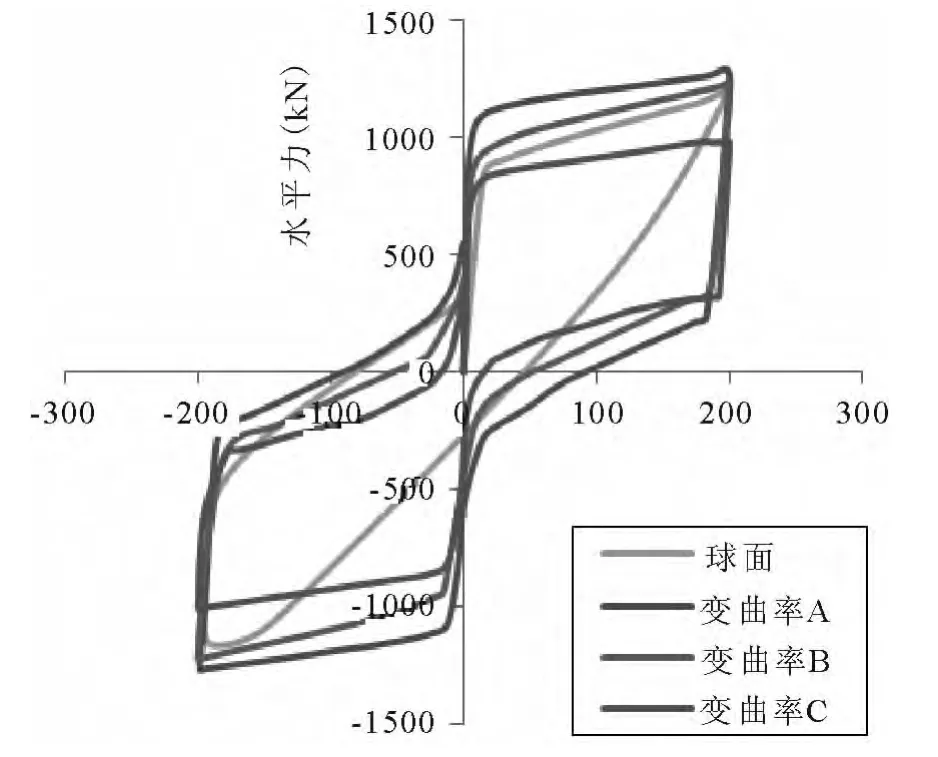
图11 不同曲率变化程度摩擦隔震支座和球面支座滞回曲线对比图
3 变曲率摩擦摆隔震支座有限元分析
3.1 ABAQUS有限元模型建立
为了研究不同变曲率程度的摩擦摆隔震支座在低周反复荷载作用下的滞回耗能能力,采用ABAQUS对上述3种不同变曲率程度的摩擦摆支座进行了数值仿真分析,为便于比较,增加了1个球面摩擦摆支座的模拟.4个支座的初始曲率半径均为4.5m,设计位移均为200mm,各个隔震支座的曲面参数如表1所示.
当支座减震球摆在消能座板内来回摆动时,限位螺栓和挡圈已失效,建模时将其略去.支座的模型示意图和剖面图(变曲率A)如图6和图7所示.支座材料为 ZG270-500,屈服强度为270MPa,极限强度为500MPa.弹性模量取2.1×105MPa,泊松比υ=0.3.由于支座各组件形状复杂导致有限元模型网格划分困难和分析不易收敛等问题,整个模型采用8结点线性六面体非协调单元(C3D8I),各组件单元网格划分图如图8所示.
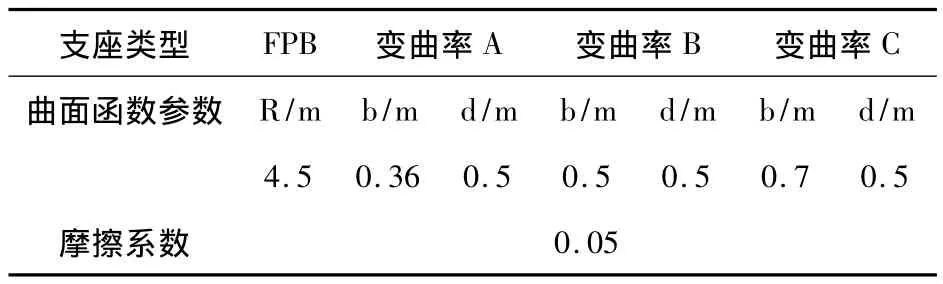
表1 摩擦摆隔震支座滑动曲面参数
支座各组件的表面之间采用接触连接,接触面的法向行为采用硬接触,并勾选“允许接触后分离”选项;接触面的切向行为遵循库伦摩擦定律,取摩擦系数为0.05.整个模拟过程设置为2个分析步:第1步:施加竖向荷载使各接触面发生接触,时间步长为1s;第2步:保持竖向荷载不变的情况下,施加水平简谐位移激励,时间步长为2s.竖向荷载恒定为W=20000kN,第2步中水平向简谐位移激励设为:D=Asin(πt),其中A为振幅(取A=0.2m,即支座的设计位移)简谐位移激励持时2s(一个周期).竖向荷载和水平位移加载时间历程如图9所示.
3.2 数值模拟结果分析
支座水平滑移达到设计位移200mm时,支座的MISES应力云图如图10所示.从应力云图可以看出:支座在滑移过程中,除个别单元的应力超过允许应力外,大部分单元应力都小于允许应力.因此,支座能够安全工作.3种不同变曲率方案摩擦支座和球面支座在水平简谐位移激励下的滞回曲线对比见图11.从图10可以看出:变曲率摩擦摆支座和球面支座的滞回曲线均较饱满,且变曲率支座的滞回饱满程度更高.当支座位移达到设计位移200mm时,变曲率A、变曲率B、变曲率C和球面的滞回环面积分别为454983kN·mm,372462kN·mm,277394kN·mm,和240992kN·mm,变曲率A、变曲率B和变曲率C支座的滞回耗能分别球是球面支座的 1.89、1.55 和1.15 倍.
4 结论
通过对滑动曲面方程的参数分析以及对不同曲率变化程度的摩擦摆隔震支座和球面支座的数值模拟,可以得出如下结论:
(1)调整滑动曲面方程中参数值,可以使所求滑动曲面满足实际工程中支座所需的任意滑动曲面要求.
(2)变曲率摩擦摆支座滞回曲线饱满,具有良好的滞回性能.且与球面支座相比,具有更强的耗能能力.
(3)通过调整方程参数,选择合适的变曲率滑动曲面方程,可以使变曲率摩擦摆隔震支座的滞回耗能达到最佳,可用于指导实际工程中支座滑动曲面的设计.
[1]Zayas V,Low S,Mahin S.The FPS Earthquake Resisting System Experimental Report[R].California:University of California at-Berkeley,1987.
[2]邓雪松,龚健,周云.变曲率摩擦摆隔震支座理论分析与数值模拟[J].土木建筑与环境工程,2011,33(1):50-58.
[3]Pranesh M,Sinha R.VFPI:An Isolation Devicefor SeimicDesign[J].Earthquake Engineering andStructural Dynamics,2000,29:603-627.
[4]Pranesh M,Sinha R.A Seismic Design of Structure Equipment Systems Using Variable Frequency Pendulum Isolator[J].Nuclear Engineeringand Design,2004,231:129-139.
[5]王建.变曲率滑动隔震防制近断层震波之实验与分析[D].高雄:国立高雄第一科技大学,2006.
[6]Pranesh M,Sinha R.Behavior of Torsionally Coupled Structures with Variable Frequency Pendulum Isolator[J].Structural Engineering,2004,130(7):1041-1054.

