解信赖域子问题的分段Hermite插值法

于海波，王希云，李 亮(太原科技大学，太原 030024)

信赖域算法是求解非线性优化问题的一类重要的数值计算方法，信赖域算法以其较强的适定性和全局收敛性受到最优化研究者们的广泛关注，一直以来是非线性规划的研究热点。对于求解如下无约束优化问题[1]，信赖域算法是一种重要的数值方法。

考虑无约束优化问题：

minF(x),x∈Rn

(1)

其中F(x)∶Rn→R是目标函数，二次连续可微，x∈Rn为待求变量。

信赖域方法的关键是每次迭代时都要求解下面形式的信赖域子问题：

(2)

其中g∈Rn为目标函数在当前迭代点的梯度，B∈Rn×n为目标函数在当前迭代点的Hessian矩阵或其近似，△∈R为信赖域半径，δ∈Rn为待求变量。当△变化时，上述信赖域子问题(2)的解δ*就形成一条空间曲线，称为最优曲线[2]。

基于信赖域子问题精确求解方法的思想，得到最优曲线的参数方程如下：

δ=-(B+μI)-g(μ≥0)

(3)

定义函数y=f(μ)=‖δ‖2=‖-(B+μI)-1g‖2，(μ≥0).则信赖域子问题的解δ*为：

当μ=0时，解δ*=-B-1g；当μ>0时，通过求解一元非线性方程：

f(μ)-△=‖-(B+μI)-1g‖2-△=0

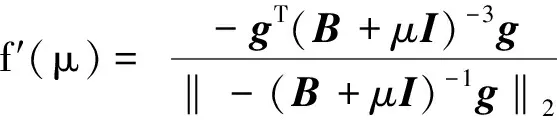
分段割线法的思想是在B正定的前提下，利用函数f(μ)的单调减性，当给定的信赖域半径△≥‖B-1g‖2时，令μ=μ0=0，得到子问题的最优解δ*=-B-1g；当给定的信赖域半径△<‖B-1g‖2时，以适当的步长不断增大μ，从而缩小函数f(μ)的值，最终找到一个最小的正整数m，使得f(μm)-△≤0，得到方程f(μ)-△=0的有根区间[μm-1,μm].通过对节点[μk,f(μk)]，(k=0,1,…,m)进行线性插值构造m条直线，连接所有直线构成分段割线，最后在插值点[μm-1,f(μm-1)]和[μm,f(μm)]之间利用线性插值构造的线性函数代替f(μ)来求解方程f(μ)-△=0的根μ*，从而求得子问题的解δ*=-(B+μ*I)-1g.

分段割线法的缺点是：在节点处分段线性插值函数一般不具有光滑性，出现尖点，并且与函数f(μ)的误差较大。

为了克服分段割线法的上述缺陷，本文利用分段三次Hermite插值函数在节点处光滑，且与被插值函数的误差较小的优点，提出了一种求解信赖域子问题的分段Hermite插值法。

1 分段三次Hermite插值法的思想

分段Hermite插值法的思想是在分段割线法的基础上，通过对节点[μk,f(μk)]，(k=0,1,…,m)进行三次Hermite插值构造m条曲线，每条曲线的方程记为Hk(μ)，(k=0,1,…,m).连接所有曲线构成分段三次Hermite曲线，最后在插值点[μm-1,f(μm-1)]和[μm,f(μm)]之间利用三次Hermite插值构造的三次插值函数H(μ)近似代替f(μ)来求解方程f(μ)-△=0的根μ*，从而求得子问题的最优解δ*=-(B+μ*I)-1g.采用这种方法构造的曲线，能够有效的避免分段割线法在节点处曲线为尖点，不光滑的缺点，进而提高了子问题(2)的解的精度。

2 分段三次Hermite曲线路径的性质分析

分段三次Hermite插值，分段线性插值及函数f(μ)的几何意义如图1所示：

图1 分段三次Hermite插值，分段线性插值及函数f(μ)的图示

从图像可以看出，分段三次Hermite插值曲线更加逼近函数f(μ).

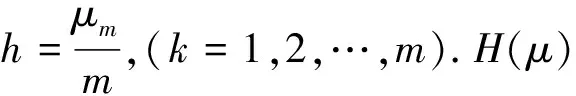
由此，可得下列结论：

定理2.1对函数f(μ)利用分段三次Hermite插值法所构造的分段曲线Γ为：

其中:

(k=1,2,…,m),则H(μ)满足：

(1)H(μ)关于μ为连续单调减函数。

(2)对任意给定的信赖域半径△<‖-B-1g‖2，一定存在μm，使得:

H(μm)-△≤0

证明：(1)由引理2.1的结论可知，H(μ)关于μ为连续单调减函数。

(2)利用(1)的结论可知结论(2)成立，证毕。

定理2.1表明，对于任意给定的信赖域半径△<‖-B-1g‖2，方程H(μm)-△=0的根存在且唯一。

下面给出本文算法3.1和信赖域算法3.2的一般框架。

3 算法框架

算法3.1(分段三次Hermite插值法)：

步0给定梯度g，正定矩阵B，信赖域半径△，适当步长h.

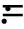
步2计算f(μk)及f′(μk)，μk=μk-1+h.在插值节点[μk-1,f(μk-1)]和[μk,f(μk)]之间使用三次Hermite插值的方法构造曲线Hk(μ)，形成分段曲线Γ.

注：步0中选取的步长h越小，由算法3.1求得的信赖域子问题(2)的解δ*就越精确。

算法3.2(非单调信赖域方法)[5]：

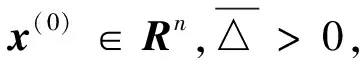
步1如果‖▽F(x(k))‖2≤ε，则算法终止，得到(1)的解x(k).否则，转步2；

步2运用算法3.1求解信赖域子问题(2)得到解δk，‖δ(k)‖2≤△k，且满足:

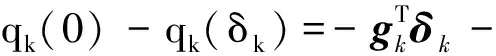
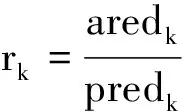
其中:aredk=Fl(k)-F[x(k)+δ(k)]

步4如果rk≥η，转步5；否则取λk为{1,β,β2,…}中使得下式成立的最大数：

令x(k+1)=x(k)+λkδ(k)，△k+1∈[c1‖δ(k)‖2,c2‖δ(k)‖2]，转步6；

步5令x(k+1)=x(k)+δ(k)，△k+1∈[‖δ(k)‖2,c3‖δ(k)‖2]；

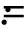
算法中Bk+1的产生可用BFGS公式。

4 数值结果

本文首先选取两个测试函数Function1和Function2，运用算法3.1对信赖域子问题进行数值实验，然后再利用算法3.2对从文献[6]和[7]中选取的无约束优化测试函数进行求解，并与采用分段割线法求解信赖域子问题的非单调信赖域算法进行了比较。

对于测试函数Function1和Function2，给定步长h=1，选取不同的信赖域半径△，利用MATLAB数学软件，采用本文算法3.1对测试函数进行数值实验，并将实验结果与分段割线算法进行比较，相关数值结果见表1和表2，其中SSD表示分段割线法，HCL表示本文算法3.1，fSSD表示分段割线法求得的测试函数最优解的数值解，fHCL表示分段三次Hermite插值法求得的测试函数最优解的数值解。fSSD-fHCL表示两者的差值，则该差值越大，表明分段三次Hermite插值法越好。

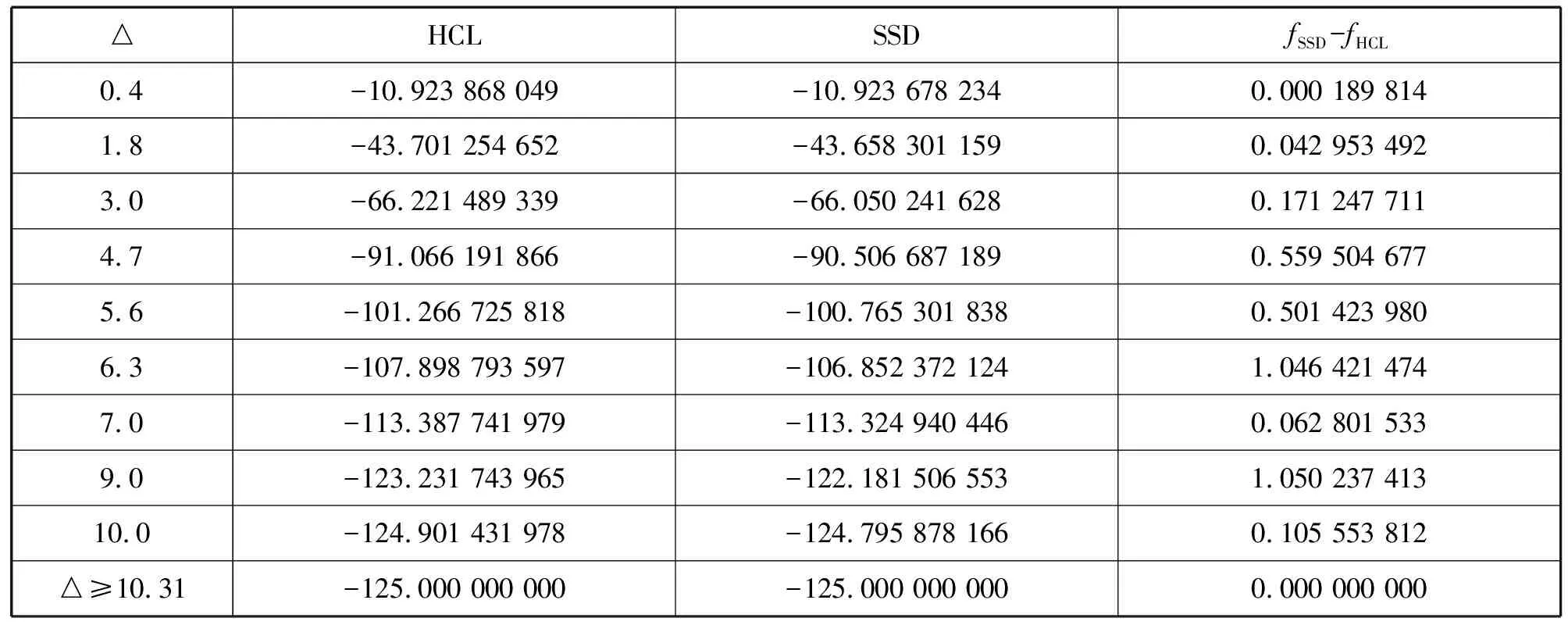
表1 Function1数值结果

从表1和表2的数值结果可以看出，当信赖域半径△≥‖B-1g‖2时，分段三次Hermite插值法与分段割线法求得的测试函数的最优解的数值结果相同(事实上，此时为牛顿算法)；当信赖域半径△≤‖B-1g‖2时，分段三次Hermite插值法的结果要优于分段割线法。因此，分段三次Hermite插值法的求解精度更高，能够更好的逼近函数f(μ)，是一种很好的求解信赖域子问题的精确解法。其中测试函数Function1的牛顿步‖B-1g‖2=10.31，Function2的牛顿步‖B-1g‖2=10.05.

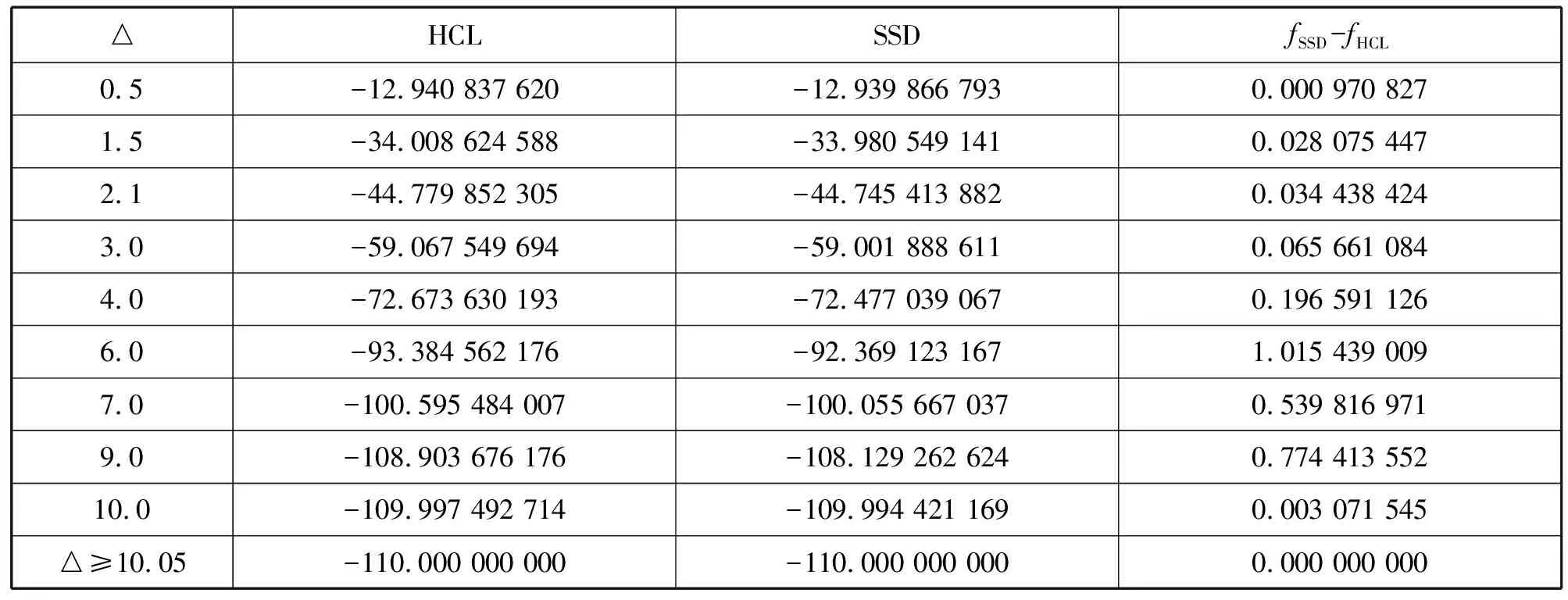
表2 Function2数值结果

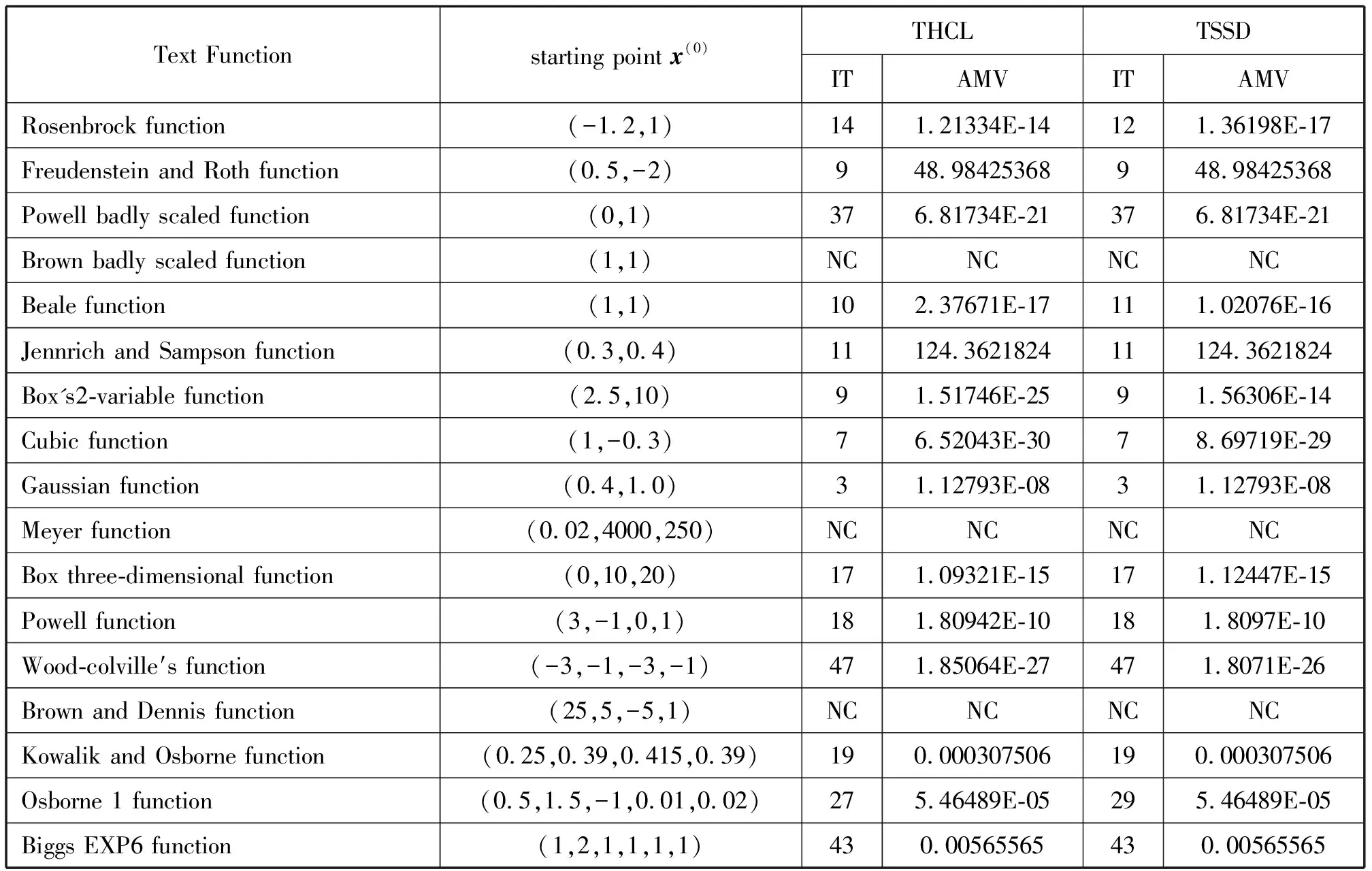
表3 Test Function数值结果

从表3的实验结果可以看出，对于不同的测试函数，采用算法THCL与算法TSSD，在满足终止条件‖▽F(x(k))‖2≤ε的前提下，对给定的初始点x(0)，两者计算所需的迭代次数及数值最优解都十分接近。总体来说，利用算法THCL求得的测试函数的最优解的数值结果要优于算法TSSD.

数值实验及理论分析都表明，运用本文提出的分段三次Hermite插值法求解信赖域子问题是有效且可行的。对于无约束优化问题，能够较好的结合非单调信赖域算法计算其最优解。

参考文献：

[1] 李亮，王希云.解信赖域子问题的分段割线法[J].太原科技大学学报，2013，34(5)：393-397.

[2] 徐成贤，陈志平，李乃成.近代优化方法[M].北京：科学出版社，2002.

[3] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，2010.

[4] FRITSCH F N，CARLSON R E.Monotone piecewise cubic interpolation[J].SIAM J Numer Anal，1980，17(1):238-246.

[5] 姚升保，施保昌.一类带线搜索的非单调信赖域算法[J].数学杂志，2003(3)：290-294.

[6] DENNIS J E，MEI H H W.Two new unconstrained optimization algorithms which use function and gradient values[J].Journal of Optimization Theory and Application，1979，28:453-482.

[7] MORE J J，GARBOW B S，HILLSTROM K E.Testing unconstrained optimization software[J].ACM Trans Math Software,1981，1(1/2)：17.

[8] 任玉杰.数值分析及其MATLAB实现[M].北京：高等教育出版社，2007.

[9] 李董辉，童小娇，万中.数值最优化算法与理论[M].北京：科学出版社，2010.