基于改进微粒群算法的单点信控交叉口配时优化

苏长慧，夏桂梅 (太原科技大学，太原 030024)

单点交叉口信号控制是我国城市各种交通信号控制的基础，也是我国目前主要的交通信号控制手段[1]，且交通信号控制的实质是交通的信号配时优化[2]。本文针对城市道路交叉口的交通流量特性，提出了单点交叉口的多目标定时控制优化方法，并与F.Webster近似公式的定时控制进行比较。仿真实验证明，由一种求解约束优化问题的微粒群算法来求解单点交叉口的多目标定时控制优化方法得到的信号配时方案更优，更适合于城市道路的单点交叉口的信号配时优化。

1 单交叉口信号配时优化模型的描述

交叉口信号控制包括评价指标[3]包含通行能力、停车次数和排队长度、时间延误、运营成本及噪声尾气排放等等，这些目标因素中道路的通行能力、时间延误、车辆的停车次数和排队长度是所有目标因素的基本量，其他的均可通过基本量导出[4]所以，本文选取时间延误、车辆的停车次数和道路的通行能力这三个目标因素建立模型，并进行交叉口的信号配时优化控制。

停车次数[5]：交叉口的车辆总停车次数为：

(1)

延误时间[6]：本文的总延误时间计算公式采用Webster延误时间的计算公式：

(2)

其中，c是信号周期，gi是相位i的有效绿灯时间，qi是相位i的交通流量(pcu/h)，yi是相位i的交通流量与饱和流量之比。

总的通行能力[7]：在现有道路条件下和交通管制下，车辆以能够接受的行车速度，单位时间内一条道路或道路的某一截面所能通过的最大车辆数，其单位是pcu/h.为了满足模型的最小值形式，计算信号交叉口的通行能力时，交通流量取其相反值。

(3)

其中：Si为相位i的饱和流量(pcu/h).

由于一天中的交通流量处于不断变化的状态，所以对于不同的交通状态，相应的交叉口信号配时控制应该随之变化。因此根据不同的交通需求，调节以上三个公式对应的权重系数，使交叉口的信号配时能达到最优。权重系数[8]如下：

(4)

2 单交叉口信号配时优化模型的建立

本文采用典型的四相位单点交叉口作为例子。交叉口包括南、北、东、西四个方向，每个方向都有直行、左转、右转三个方向的交通流。

图1 交叉口示意图

相位信号配时方案见图：

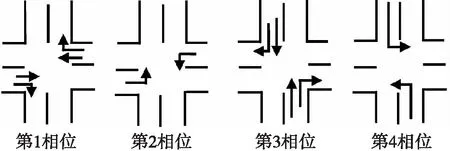
图2 典型的四相位图

把通行能力最大化，总延误时间和车辆的停车次数最小化作为优化目标，利用实时变化的权重系数，依照实际道路的交通流量数据来建立目标函数：

(5)

s.t.

其中，i是交叉口的相序；gmin是第i相位的最小有效绿灯时间，s；gmax是第i相位的最大有效绿灯时间，s；li是第相位的损失时间，s；cmax是最大周期时间，s.

为了避免饱和度过大或过小在上述模型中我们给出了道路交叉口饱和度k=cyi/gi的约束条件，且本文设定了最大饱和度和最小饱和度参数0.95和0.75，它们是可变的。

3 一种解决约束优化问题的微粒群算法

根据文献[9]的原理：一种解决约束优化问题的微粒群算法是专门针对约束优化问题而言的，是在标准微粒群算法的位置和速度更新公式(6)的基础上进行改进的。

(6)

改进算法为了让t+1代的微粒更靠近全局最优值，把t+1代不满足约束条件的微粒xi(t+1)用映射点xc代替。映射点xc是在由pi(t)、xi(t)和pg(t)所构成的形心的连线上选取的，形心的计算公式为式(7)。若xc不在可行域内，则用公式 (8)、(9)产生重新映射点，到映射点落在可行域内为止。公式如下：

xc=[pi(t)+xi(t)+pg(t)]/3

(7)

xr1=λ1xr1+(1-λ1)pg

(8)

xr2=λ2pg+(1-λ2)xr2

(9)

初始的xr1，xr2的计算公式为：

其中，i代表微粒；t代表迭代次数；g代表每一代中的最优微粒；pi代表历史最优位置；pg表示所有微粒的最优位置；xc表示形心位置；xr1是xc和pg连线上的某一位置；xr2是pg和2pg-xc连线上的某一位置；c1，c2是学习因子；w是惯性权重；rand()，Rand()是[0，1]内的随机数。算法步骤：

1)参数的设置及初始化；

2)计算每个微粒的适应度；

3)根据公式(6)更新每个微粒速度，更新每个微粒新局部最优值Pi和新全局最优值Pg；

4)判断速度是否超出Vmax，若超出，去边界值。判断每个微粒是否满足约束条件，若满足，则转步7)，否则转步5)；

5)根据公式(7)计算形心位置，判断是否满足约束条件。若满足，则转步7)，否则根据公式计算xr1、xr2；

6)根据公式(8)、(9)计算xr1、xr2判断是否满足约束条件。若都不满足，转步6)，否则若其中之一或都满足，则转步7)；

7)若未达到结束条件，返回步2).

4 仿真实例

以典型的四相位单点交叉口为例，对交叉口相位的有效绿灯时间进行配时优化。交叉口流量流向如表1所示[10]：

算法参数设置：种群规模20，最大迭代次数500次，最大评价数10 000，惯性权重wmax=0.9，wmin=0.4 ，加速因子c1=c2=1.8.

交叉口各相位的最小有效绿灯时间和最大有效绿灯时间分别为10 s和90 s，最大周期为180 s，总的损失时间为24 s.

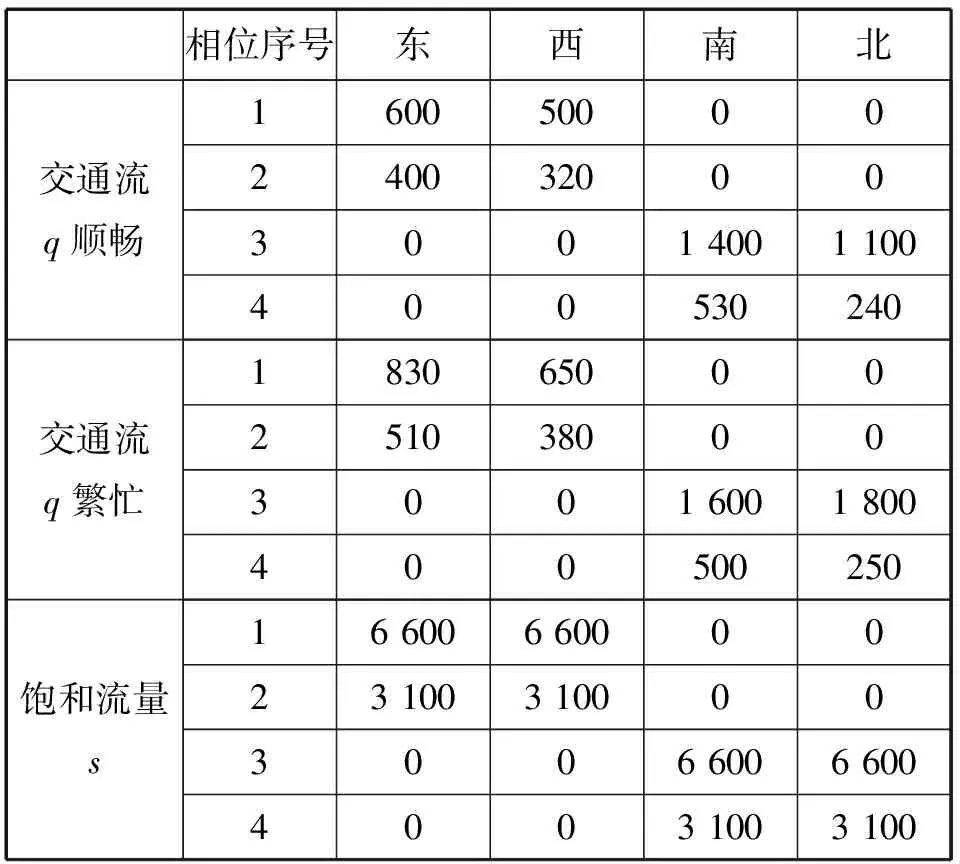
表1 交通状态顺畅、繁忙时各方向交通流数据

采用Webster算法和一种求解约束优化问题的微粒群算法求解模型，得信号配时优化方案，计算结果见表2.

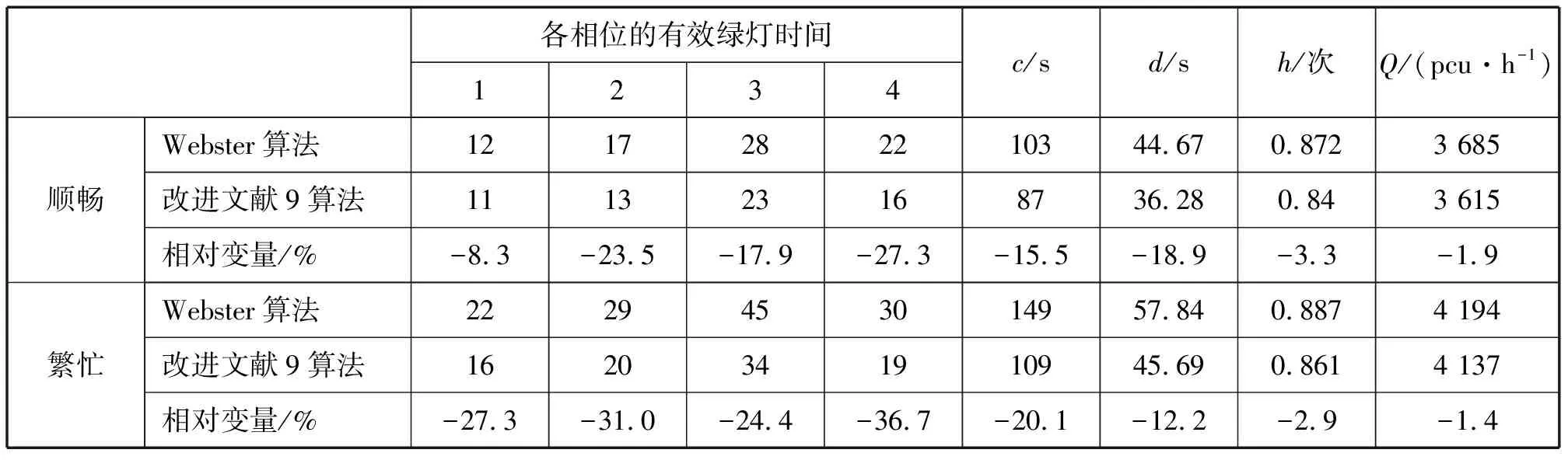
表2 两种算法的实验结果

文章采用改进的文献9算法求解模型，得到新的信号配时方案，并与传统的Webster算法进行比较。由表2可知：

(1)在交通处于顺畅状态的情况下，与Webster算法相比较，改进算法的总延误降低了18.9%；停车次数减少了3.3%；周期减小了15.5%；通行能力降低了1.9%.

(2)在交通处于繁忙状态的情况下，与Webster算法相比较，改进算法的总延误降低了12.2%；停车次数减少了2.9%；周期减小了20.1%；通行能力降低了1.4%.

由此可见，不论是在交通顺畅还是繁忙时，改进算法使得总延误时间和车辆的停车次都有明显的下降；并且由案例知，在损失时间一定时，周期的减小，会使得道路的理论通行能力有所下降，所以改进算法使得道路的通行能力略有下降。这说明改进算法求解信号配时方案是有效可行的，而且证明改进算法得到的信号配时方案更优，更能满足交通流量的实际需要，能够更好的进行信号控制优化。

5 结束语

本文以典型的城市四相位单点交叉路口为例，把总延误时间、车辆的停车次数的最小化和道路的通行能力的最大化作为目标函数，利用改进算法对函数模型进行求解，得到信号配时方案，并对单交叉口的信号配时优化进行控制。仿真结果证明，改进算法是有效的和可行的，且与传统的Webster算法进行比较，改进算法更能有效的在各种状态下减少总延误时间和车辆的停车次数，提高道路的通行能力。

同时与Webster算法的结果相比较，改进算法使得在绿灯时间到达的车辆，以适当的速度，较少的延误时间，较少的停车次数通过交叉口；改进算法使得交叉口的通行能力也得到有效的改善。这说明根据实际的交通流规律，由改进算法得到的信号配时优化方案更合理，更适合于单点交叉口的交通控制需求。

参考文献：

[1] 李卫平.智能交通技术应用 [M].北京：人民交通出版社，2006.

[2] 隋亚刚，李正熙，刘小明，等.城市智能交通控制理论与应用 [M].北京：中国水利水电出版社，2006.

[3] 张本，商蕾，高孝洪.基于遗传算法的交叉口信号配时多目标优化[J].武汉理工大学学报，2010，34(4)：845-848.

[4] 刘金明.基于多目标规划的城市道路交叉口信号配时研究 [D].北京：北京交通大学，2011.

[5] 顾怀中，王炜.交叉口交通信号配时模拟退火全局优化算法 [J].东南大学学报，1998(3)：68-72.

[6] 尹宏宾，徐建闽.道路交通控制技术 [M].广州：华南理工大学出版社，2001.

[7] 杨佩昆，吴兵.交通管理与控制[M].北京：人民交通出版社，2003.

[8] 廖诗琪，汪云龙.单点交叉口交通信号配时模型及遗传算法[J].公路与汽运，2012(5)：45-48.

[9] 孙超利，谭瑛，潘正祥，曾建潮.一种求解约束优化问题的微粒群算法 [J].太原科技大学学报，2010，31(6)：453-457.

[10] 曹娟娟，邵维.基于改进粒子群算法的多目标单交叉口信号优化控制 [J].长沙大学学报，2012，26(2)：69-71.