基于属性熵和加权余弦相似度的离群算法
刘爱琴,荀亚玲 (太原科技大学计算机学院,太原 030024)
离群数据挖掘是数据挖掘领域中的一个重要分支,其目的是找出隐含在海量数据中的相对稀疏而孤立的异常数据模式。离群数据挖掘有着广泛的应用,例如网络非法入侵检测及天文学上新星体发现等[1]。
目前,很多数据的维数非常高,有的甚至高达上百维,如何提高高维数据离群挖掘的效率是目前研究的一个重点。在高维数据空间中,数据的稀疏性意味着每个点都可以看作离群数据,因此传统的基于统计的、基于分类的、基于距离以及基于聚类等方法的离群数据挖掘算法不再能有效发现离群数据[2]。当前用于高维离群检测的方法有基于信息理论的、基于余弦相似度、基于子空间的、基于基尼指标的、基于属性相关性分析等算法。基于信息理论的离群挖掘算法通过分析数据集的信息熵来进行离群挖掘,此类算法基于这样的假设:离群点增加了数据集的不规则性。典型的算法有基于信息熵的快速贪婪算法[3]和信息熵度量的离群数据挖掘算法[4]和基于信息熵的相对离群点的检测方法等[5]。ANNA K使用余弦相似度来度量高维数据中的离群对象,也是一种比较有效的方法[6]。所谓子空间技术是针对全空间而言的。在数据的所有属性中,选取若干维属性所组成的数据空间为子空间。离群挖掘即找到容易识别离群点的子空间,子空间技术对高维数据效率很高。AGARWAL C等提出一种基于子空间的离群数据挖掘算法[7],该算法的基本思想是首先将高维数据投影到低维子空间,然后在子空间中考察数据的行为,并利用遗传算法搜索稀疏子空间,把稀疏子空间中的数据定义为离群数据,但搜索子空间的进化算法是随机搜索算法,并不能确保搜索到所有的异常子空间,算法的完备性和准确性无法得到保证。ZHANG J F等利用概念格作为子空间描述工具,提出了一种低维子空间离群数据挖掘方法,并利用概念格和稠密度系数提高了算法的正确性和完备性[8]。王磊等利用属性相关性分析思想,删除了高维数据集中的冗余属性,并结合并行运算及微粒群算法,提高了离群检测的准确性和效率[9]。石岩等人在属性相关分析的基础上,采用基尼指标作为离群度量因子,挖掘出不同离群程度的数据点[10]。
1 相关研究
为了提高高维离群检测的精度,倪巍伟等人将子空间和信息熵的概念相结合,提出了基于局部信息熵的加权子空间离群点检测算法(SPOD)[11]。其相关的概念定义如下:
假设数据集D=(O,A),对象集O={o1,o2,…om},属性集A={A1,…Ad},对象o∈O关于属性Ai的值记为∏Ai(o).
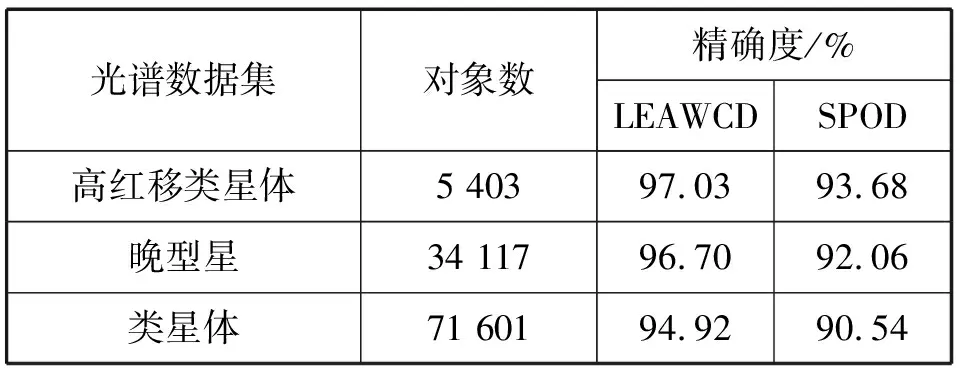
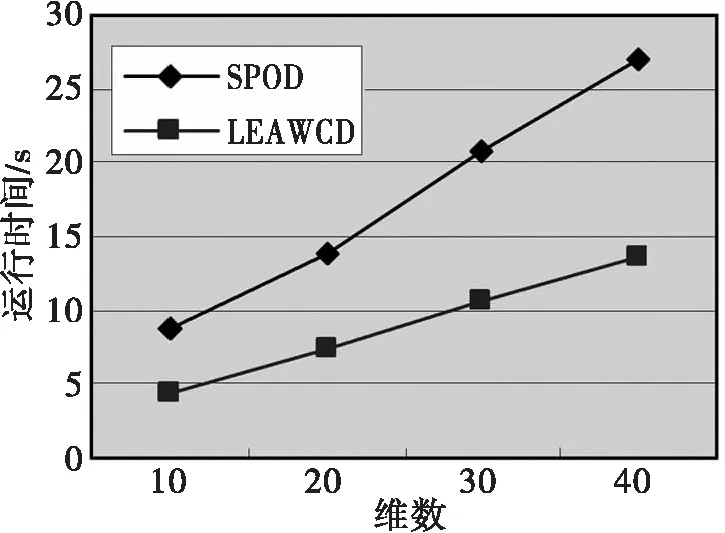
定义1(对象o的k-距离)。存在对象p∈O,使得至少有k个对象p′∈O满足dist(o,p′)≤dist(o,p′),并且最多有k-1个对象p′∈O满足dist(o,p′) 定义2(对象o的k-邻域)。对象o的k-邻域是其邻居对象的集合,即: δ=Nk(o)={q∈O|dist(o,q)≤k-dist(o)} (1) 定义3(局部属性熵)。对o∈O,Ai∈A,对象o关于属性Ai的局部信息熵定义为: (2) 其中: dmax=max{dist(∏Ai(o),∏Ai(q))|q∈Nk(o)} dmin=min{dist(∏Ai(o),∏Ai(q))|q∈Nk(o)} SPOD算法是一种检测精度较高的离群挖掘算法,但存在以下不足:(1)依据局部属性熵而设置的属性权重为一固定值,并不能反映属性本身的离群程度,且需要人为设置;(2)需两次计算每个对象的k-邻域。首次计算各对象的k-邻域δ其目的是最终确定每个对象各个属性在该邻域δ内的权重参数ω.其后将会根据权重ω再次计算每个对象的k-邻域δ′,并计算加权密度等,检测基于邻域δ′的局部离群点。计算邻域是SPOD算法中最耗时的一个步骤,其时间复杂度为:O(d×m2).两次计算邻域直接造成算法运行时间变长,运算效率降低。此外,k-邻域δ′及加权密度等相关量的计算是基于权重参数ω进行的,而权重ω是根据另一不同的邻域k-邻域δ内的离群属性而设置的,因此邻域δ′及其相关量的计算理论上并不是完全必要和合理的。 本文给出一种基于属性熵和加权余弦相似度的离群数据挖掘算法LEAWCD.该算法首先根据局部属性熵分析每个对象各个属性在k-邻域δ内的属性偏离度,并据此自动设置相应的属性权向量;然后使用对高维数据更有效的加权余弦相似度来度量各对象的离群程度,从而实现各对象在k-邻域δ内的局部离群点检测。 在SPOD算法中,若对象o关于属性Ai的局部属性熵大于其k-邻域δ内各对象关于Ai的属性熵均值,则将属性Ai视为对象o在k-邻域δ内的离群属性。文中引入属性偏离度来进一步判断和衡量属性离群的程度。 定义4(对象o的局部属性偏离度)。对象o关于属性Ai的局部属性偏离度定义为: (3) 其中:分子 LEAAi(o)为对象o关于属性Ai的局部属性熵,分母为对象o的k-邻域δ内所有对象关于属性Ai的局部属性熵均值。当deviateLevel(o,Ai)大于1时,表明属性Ai为对象o在k-邻域δ内的离群属性,且其值越大,说明该属性离群的程度越高。 在文献[11]中,将不同属性分别赋以不同的权值。对于离群属性设置为一固定的权重λ(λ>1),而非离群属性权重设为1.由于权重λ的值需要人为设置,因此挖掘结果易受人为因素影响,且固定的权重值无法精确反映属性离群的程度。本文使用属性权向量对不同属性的权重进行定义。 (4) 而 其中,当deviateLevel(o,Ai)>1时,根据属性偏离度的定义,属性Ai为离群属性。此时权重参数不再需要人工设置,而是设定为该属性的属性偏离度,以直接反映该离群属性的离群程度。deviateLevel(o,Ai)≤1时,属性Ai为非离群属性,仍保持权值1不变。 (5) (6) 参照文献[6],对象的局部加权离群因子定义如下: (7) ω1KOF用于度量对象的局部离群程度,计算所有对象的ω1KOF,并按升序排列,离群因子最小的n个对象就是所求的局部离群点。 输入:数据集D,邻域对象数k,离群点个数n. 输出:离群点集 2.运用式(6),计算每个对象在其k-邻域δ内的加权中值向量,并用式(7)确定每个对象的局部加权离群因子ω1KOF; 3.依据局部加权离群因子ω1KOF采用快速排序法将各对象按升序排序; 4.输出前n个对象,即为所求离群点集。 在PentiumIII-1.0G CPU,256M内存,Windows XP操作系统,DBMS为ORACLE9i环境下,用Visual C++6.0实现了SPOD和LEAWCD算法。实验中采用国家天文台提供的晚型星、高红移类星体以及类星体三个天体光谱数据集。 (1)算法的精确度比较 为了验证LEAWCD算法的正确性,选取SPOD[11]算法作为比较算法。其中,这三个数据集的维数为44维,两种算法需共同设置的参数为邻域中点数目k=7;另外,SPOD算法还需设置离群属性权重λ=1.5. 表1 算法的检测精确度比较 (2)算法对数据集维度的伸缩性 为了测试算法对数据集维度的伸缩性,在高红移类星体光谱数据中分别取维数为10、20、30、40维对SPOD和LEAWCD算法的运算效率进行比较。实验中,除维数外,其余参数的设置与测试算法精确度的实验相同。由图可知,在不同维度下,LEAWCD算法的运行时间基本上为SPOD算法的一半。这是因为对于这两个算法,计算邻域都是最耗时的步骤,其复杂度为O(d×m2).在SPOD算法中,需要两次计算k-邻域,而在本文算法中,仅需计算一次k-邻域,因此本文LEAWCD算法其运行时间大约为SPOD算法的一半。 图1 算法对数据集维数的伸缩性 目前的离群数据挖掘算法应用到高维数据时会出现“维灾难”,效率较低。LEAWCD算法通过属性偏离度自动设置权重,并使用对高维有效的加权余弦相似度来度量各对象的离群程度,实现了高维离群点检测。理论分析和实验结果表明,LEAWCD算法在减少用户依赖,缩短运行时间,提高检测精度上具有较明显优势。 参考文献: [1] 薛安荣,鞠时光,何伟华,等.局部离群点挖掘算法研究[J].计算机学报,2007,30(8):1-9. [2] ARINDAM B,VIPIN K.Anomaly detection:a survey[J].ACM Computing Surveys (CSUR),2009,41(3):1-58. [3] HE Z Y,XU X F,DENG S H.A fast greedy algorithm for outlier mining[C]∥Proceedings of PAKDD′2006(LNAD918).Singapore:NTU,2006:567-576. [4] 张贺,蔡江辉,张继福.信息熵度量的离群数据挖掘算法[J].智能系统学报,2010,5(2):150-157. [5] 于绍越,商琳.基于信息熵的相对离群点的检测方法:ENBROD[J].南京大学学报,2008,44(2):212-218. [6] ANNA K.A fast outlier detection strategy for distributed high-dimensional data sets with mixed attributes[J].Data Mining and Knowledge Discovery,2010(20):259-289. [7] AGARWAL C,YU P S.An effective and efficient algorithm for high-dimensional outlier detection[J].The International Journal on Very Large Data Bases,2005,14(2):211-221. [8] ZHANG J F,JIANG Y Y,CHANG KAI H,et al.A concept lattice based outlier mining method in low dimensional subspaces[J].Pattern Recognition Letters,2009,30 (15):1434-1439. [9] 王磊,张继福.基于属性相关分析的离群数据并行挖掘算法[J].太原科技大学学报,2011,32(5):364-368. [10] 石岩,刘爱琴,张继福.一种基于基尼指标的高维数据离群挖掘算法[J].太原科技大学学报,2013,34(3):161-165. [11] 倪巍伟,陈耿,陆介平,等.基于局部信息熵的加权子空间离群点检测算法[J].计算机研究与发展,2008,45(7):1189-1192.2 基于属性熵和加权余弦相似度的离群数据挖掘算法
2.1 局部加权离群度量因子的计算




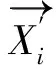
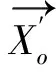

2.2 算法的描述


3 实验
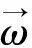
4 结束语

