导管桨-舵系统水动力性能研究

许颂捷，王贵彪，王 伟

（1.浙江海洋学院水产学院，浙江舟山 316022；2.浙江省海洋水产研究所，浙江舟山 316021；3.浙江海洋学院船舶与海洋工程学院，浙江舟山 316022）

布置于船体尾部的螺旋桨与舵，由于位置接近容易造成相互间的干扰，这种互扰可能造成螺旋桨的推进效率降低、舵表面产生空泡、噪声等问题，进而影响船舶的快速性与操作性[1]。目前，国内外许多研究者已经对这种干扰做了深入研究，沈兴荣等[2]较早运用CFD方法对桨-舵系统进行研究，针对桨-舵之间的间距进行详细研究，分析间距大小对于舵表面压力的影响，并对舵表面空泡位置进行预测。何苗等[3]运用包含两个升力体的面元法理论，对桨-舵系统进行定常与非定常的水动力性能预报，取得良好精度。王展智等[4]以四桨两舵作为研究对象，重点研究了舵体的位置变化对螺旋桨水动力性能的影响。

目前，对于桨-舵干扰问题研究绝大多数针对普通螺旋桨，对于导管桨-舵干扰的水动力性能研究依然较少。由此，本文以42 m拖网渔船对应的导管桨-舵系统为研究对象，运用ANSYS-Fluent软件对导管桨敞水特性进行预报，并与实验结果进行比较分析，验证数值方法的可靠性。在此基础上，对导管桨-舵系统进行数值模拟，并分析转舵角对导管桨-舵系统的影响规律。

1 CFD基本理论及数值计算模型

1.1 CFD基本理论

连续性方程和 RANS 方程如式(1)和(2)所示。式中为雷诺平均速度，u′i为脉动速度，而为雷诺应力。

RNG k-ε湍流模型通过修该湍流粘度，考虑了平均流动中的旋转及旋流流动情况[5]，因而本文选用RNG k-ε湍流模型来处理螺旋桨的旋转运动问题。其关于k与ε的输运基本方程如式(3)、(4)所示，其详细的推导过程和参数选取可参见文献[6]。

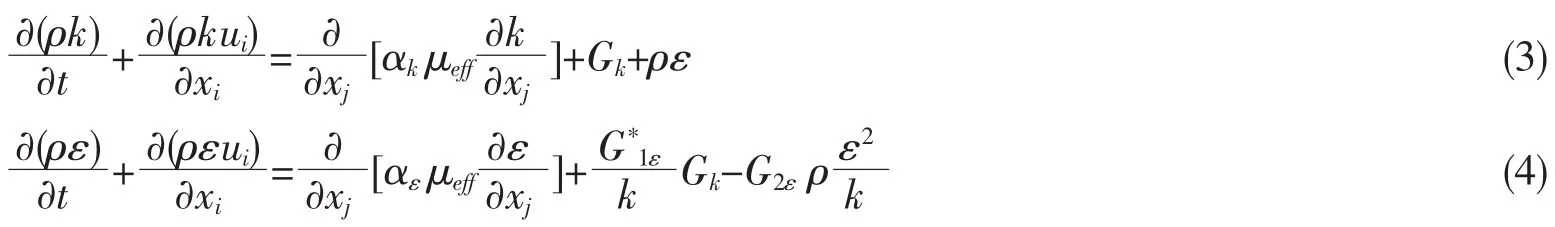
1.2 数值计算模型

42 m拖网渔船的导管螺旋桨与舵尺寸见表1，舵杆距桨轴中心线为1.3 m，其参数如表1所示。在Gambit前处理中以12.5的缩尺比建立的几何模型，并导入ANSYS-ICEM中，如图1所示。

表1 导管桨、舵几何参数Tab.1 Geometry parameters of ducted propeller and rudder

计算域设置如图3所示，由2个子域组成，分别是包含导管内壁的螺旋桨域、导管外壁至远场的整个流场域。进口设置于桨前2.5D（导管直径）处；出口设置于桨后9D处；整个远场区域直径取6D。在ANSYS-ICEM中全部采用结构网格划分桨-舵系统的网格，网格总数147万，如图2与3所示。

边界条件的设置如图4所示：在入口设置为速度入口；出口设置为压力出口；螺旋桨区域设置为旋转域；导管外壁的整个流场设置为静止域；对于静止域以及旋转区域的交界面采用interface来处理；舵壁面则设置为速度无滑移壁面。

图1 导管桨-舵系统三维模型Fig.1 3D model of propellerrudder system

图2 导管桨-舵系统表面网格Fig.2 Mesh of propeller-rudder system

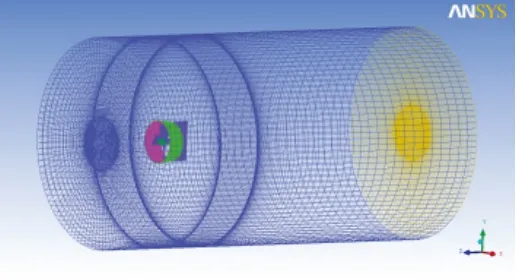
图3 导管桨-舵系统计算域网格Fig.3 Mesh of calculation domain

图4 计算域边界条件设置图Fig.4 Calculation domain of propeller-rudder system

2 计算结果与分析

2.1 导管桨敞水性能计算结果验证

图5 导管桨敞水性能曲线Fig.5 Open water performance curves of ducted popeuer

计算采用RNG k-ε湍流模型，同时采用尺度化壁面函数来处理近壁面并考虑壁面粗糙度的影响，数值离散则采用二阶迎风差分格式，螺旋桨区域采用MRF法绕Z轴正向旋转。对导管桨进速系数分为0.3、0.5、0.7、0.8、0.9，并根据J=VA/nD推算出各进速系数对应的流速度，其中转速恒为n=10 r/s。计算得到的敞水性能曲线与是试验结果的比较如图5所示。

图5中横坐标为进速系数J=VA/nD；纵坐标为总推力系数Kt=（Td+Tj）/ρn2D4；导管推力系数 Ktn=Td/ρn2D4；扭矩系数 Kq=Q/ρn2D5；推进效率 η=JKt/2πKq。Td为导管上的推力，Tj为螺旋桨上的推力，n为转速，ρ为水的密度，D为螺旋桨直径。

由图5可知，数值计算结果与试验结果的特征曲线的变化趋势基本一致，推力系数Kt、Ktn及扭矩系数Kq随着进速系数J增大而减小；J=0.8附近为整个推进效率的“拐点”位置。此外，所有水动力特征系数的计算值与试验值吻合较好，相对误差均在10%以内，导管推力系数相对误差为4.37%，最大误差为J=0.9时的Kt的9.72%。这说明文中所选用的数值方法适合导管桨敞水性能的求解，可用于导管桨-舵系统的预报与分析。

2.2 导管桨-舵系统数值结果分析

对于整个导管桨-舵系统而言，舵体产生的推力或阻力均会影响整个桨系统甚至至船体的效率。因此在分析整个系统的推力、敞水效率时需要考虑舵叶部分的推力，即按照下式计算：

式中：Td为导管上的推力，Tj为螺旋桨上的推力，Tr则为舵体上的推力。

具体计算结果如图6所示：导管桨敞水与导管桨-舵系统数值计算得到的特征曲线的变化趋势基本一致。由于舵的存在，导管的推力系数较敞水有所下降，而螺旋桨的扭矩系数和推系数均比敞水时大，其中扭矩系数幅度均值约5.2%。而计入舵后的导管桨的效率值较之敞水效率有所减小，但都在J=0.8位置出现“拐点”。

对于渔船而言，低速为其主要工况，故选取J=0.3的拖网工况研究舵的存在对导管桨桨后流场的影响。由桨后流场轨迹线图可以发现：受舵的影响，桨后区域流体质点的运动轨迹发生明显变化，桨后尾流旋转消失，呈现出沿着舵体表面向上下延伸的现象。

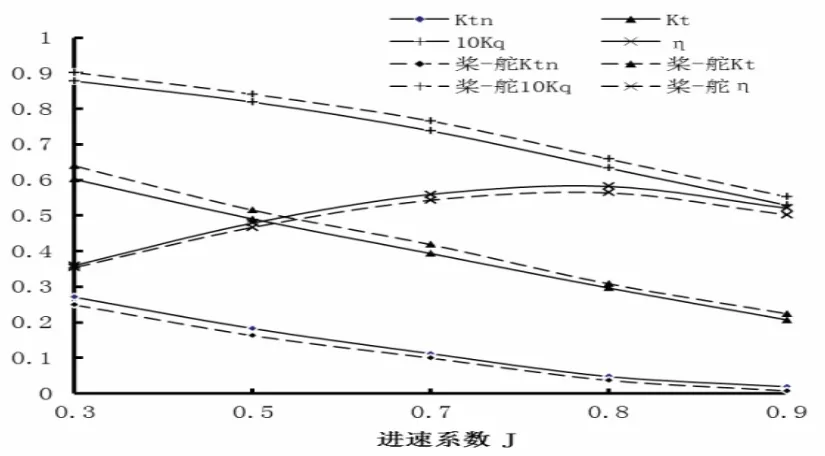
图6 数值计算得到的带与不带舵的敞水性能曲线Fig.6 Open water performance curves of numericalsimulation(with and without rudder)

图7 桨后流场轨迹线图Fig.7 Streamline behind ducted-propeller

图8为拖网工况J=0.3时，Z=-0.067 m平面（位于导管与舵之间）与Z=-0.22 m平面（位于舵后）处的轴向速度分布图。

由（8-a）与（8-b）可知，导管内外壁处轴向速度呈现层状分布现象，但无舵情况下此现象更为明显；在有舵情况下，导管内桨叶区域速度分布向上下拉伸。由（8-c）与（8-d）可知，舵的存在致使流场发生显著变化，舵体的左侧面下方及右侧面上方出现呈中心对称状的加速域与减速域。

图8 桨后轴向速度分布图Fig.8 Axial velocity profile behind propeller

2.3 舵转角对导管桨水动力性能影响

渔船在航行中，为避免偏离预定的航线，需要通过转舵方式来保持船舶的航向。因此，分别选取左转舵工况下舵角分别为 8°、15°、30°、45°进行水动力性能分析。仅对几何模型进行修改，保持网格划分、求解参数等设置与原先一致。

具体计算结果如图9所示。从图中我们可以发现：当舵角不断增大，整个系统的推进效率随之减小；同时随着转舵角增大，推进效率的下降速率加快。

3 结论

本文对粘性流场中导管桨-舵系统展开了水动力性能研究，通过上述的分析，可以得出以下结论：

（1）由于舵的影响，螺旋桨的扭矩系数及推力系数有所增大，然而导管的推力系数却呈现出减小趋势。

（2）考虑舵以后，导管桨的尾流场与敞水时变化非常明显：桨后尾流旋转消失，呈现出沿舵两舷侧向上下方向延伸现象；所取Z=-0.22的舵后截面，速度分布与导管桨敞水时分布差异明显。

（3）左转舵工况下，随着舵角增大，整个系统的推进效率随之减小；同时随着转舵角增大，推进效率的下降速率加快。

然而，本文仅仅初步地探讨了采用CFD软件计算了导管桨和舵系统的水动力性能，对计算结果的分析还不够深入。在今后的工作中，应对存在问题的地方加以改善，并将船体对导管桨-舵系统水动力性能的影响加以考虑。

图9 不同舵角下桨-舵系统效率比较图Fig.9 Efficiency of propeller-rudder system at different angle

[1]黄 胜.桨舵干扰的理论与实验研究[M].哈尔滨:哈尔滨工程大学出版社,2007.

[2]沈兴荣,冯学梅,蔡荣泉.均流中大型集装箱船桨舵干扰粘性流场的数值计算研究[J].船舶力学,2009,13(4):540-550.

[3]何 苗,黄 胜,王 超,等.桨舵系统非定常水动力性能预报方法研究[J].华中科技大学学报:自然科学版,2011,39(10):41-45.

[4]王展智,熊 鹰,姜治芳.舵的布置对螺旋桨水动力性能的影响[J].华中科技大学学报:自然科学版,2012,40(8):53-56.

[5]ANSYS FLUENT User's Guide.Fluent Inc.,2011.

[6]王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.