基于滑模控制的ROV深度方向轨迹跟踪研究

杨俭健，付宗国

（1.浙江海洋学院船舶与海洋工程学院，浙江舟山 316022;2.浙江海洋学院水产学院，浙江舟山 316022）

随着科学技术的显著提高，潜水器在水下探索的范围变得越来越大。在海洋开发过程中，水下机器人将在海洋环境的探测与建模、海洋目标的水下探测与识别、定位与传输等方面发挥重要的作用[1]。如何有效控制水下机器人的运动和姿态是值得思考和研究的。

水下机器人的控制系统具有强非线性、强耦合、时变以及多自由度的特点[2]。由于水动力系数的不确定性和复杂性以及涌流环境的变化性，人们很难得到精确的控制模型。因此，这些因素导致了小型ROV在深度方向的运动控制提供了一定的难度。

然而，很多学者在水下机器人的深度控制方面做了大量的研究工作，并总结了许多行之有效的控制策略。主要有如下的几个方面：熊华胜等[3]引入了鲁棒控制策略，该控制器在减轻或克服水下机器人运动模型的不确定性，严重非线性和外界干扰等方面具有明显的效果，具有很好的动态性能，系统的鲁棒性强，但是系统反应时间过长，难以实现实时控制。HONG等[4]对自治水下潜器设计了一个深度控制器设计，该控制器采用了双回路控制方案，克服了角度倾斜的问题。该控制器对于系统提供了良好的稳定性，但双回路的控制方案比较难控制。ZANOLI等[5]提出了基于PID和模糊控制的不同控制方案解决位置反应中超调量的减少的问题，两种方案相比较显示了控制方案的优越性。BESSA等[6]研究了对于在建模不精确和外部干扰的情况下，基于滑模控制策略和加强由对不确定性（干扰）补偿的一种自适应模糊算法被提出。用李雅普洛夫稳定性定理和Barbalat法则来分析证明闭环系统的稳定性和收敛性，呈现的数值结果为了阐述控制系统性能。SOYLU等[7]对于水下机器人的轨迹控制提出了一个无颤振滑模控制器。YUH[8]对水下机器人的运动控制运用神经网络控制理论，得出该方法是有效的，但是系统的稳定性却无法保证。HEALEY等[9]对于水下机器人的运动控制问题设计了一个滑动模态控制器，结果表明该方法对于系统的参数以及环境参数的变化具有良好的鲁棒性，但属于离线控制。

而本文是在前面学者的研究基础上，针对未知海流等外界干扰，系统不确定性信息对小型ROV深度控制造成不利影响，用滑模变结构控制的方法设计了深度控制器来完成水下机器人的位置轨迹的跟踪，从而对水下机器人实现理论上的定位。

1 小型ROV深度方向运动数学模型的建立

本文研究的是水下机器人垂直面的深度控制问题，可以把水下机器人的六自由度数学模型[10]进行相应的简化从而得到垂直面上的动力学方程。

在简化过程中，作出以下假设：

（1）水下机器人在垂直方向的运动过程中，速度较低。水下机器人在执行定深任务时，不发生运动状态间的耦合，各运动状态之间是相互独立的。

（2）考虑到水下机器人本身的对称性，为了使模型简化，采用线性模型，忽略非线性水动力项，不考虑水平面和垂直面间的耦合，将坐标原点取在水下机器人的重心处就可以得到垂直面线性动力学方程组[11]:

考虑到一般水下机器人在垂直方向上只有一个推进器，且在垂向轴线上没有纵倾角的控制，所以水下机器人在垂向运动时纵倾角变化可以忽略。因此，我们只考虑垂直方向上的单个方程可以简化为如下形式：

其中z为垂直方向上的位移，U为基准速度，Tz为垂向的推力。具体的各个参数可以参考文献[11]因此，我们可以得到各个参数，在式（4）中取 m=17.25 kg，Zw˙=-0.0215 kg，Zw=-566.8722 Ns2/m2，Zww=-73.1629 Ns2/m4。

2 滑模变结构控制器的设计

根据前面所简化的数学模型式(4)，假设U=1时，系统的数学模型可以写为如下形式：

式中x1表示的是深度，d(x,t)为所加的外部干扰，把设定的参数代入到式（5）得:f(x,t)=-32.8144x2-4.2352，b(x,t)=1，若外部干扰为 d(x,t)=2sin(t)。

2.1 在理想情况下的滑模反演控制器的设计

定义1位置误差：z1=x1-zd（zd为指令信号）

通过控制律的设计，使得系统满足了李雅普诺夫稳定性理论条件，z1和z2是以指数形式渐进稳定的，从而保证了系统具有全局意义下指数的渐进稳定性。

2.2 在有干扰下的滑模自适应反演控制器的设计

假设位置指令为Yd，控制器设计如下：

对于位置跟踪，跟踪误差为：z1=Y-Yd

定义9切换函数为：σ=k1z1+z2(k1＞0)

由于控制器采用3F的上界，当F为未知时，易造成斗振。

将控制器表达式（17）代入到表达式（16）可以得到：

式（23）保证跟踪误差在有限时间内收敛为零，并保证滑模切换函数σ最终有界稳定，实际控制量可以保证σ收敛到原点附近的一个小领域内，满足所需的滑动模态。

通过控制律的设计，使得系统满足了李雅普诺夫稳定性理论条件，z1和z2是以指数形式渐进稳定的，从而保证了系统具有全局意义下指数的渐进稳定性。

3 仿真研究

在这里取指令信号zd=sin(6πt)，图1控制器的控制律取c1=90，c2=300；图2控制器的控制律c1=300，c2=300。初始状态x(0)=［00 ］。通过MATLAB-SIMULINK进行仿真[12]从而得到的位置轨迹跟踪曲线如图1、2 所示：

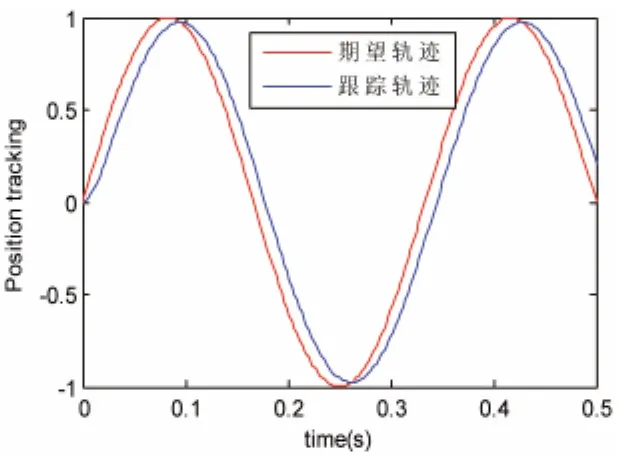
图1 控制律c1=90，c2=300Fig.1 Control law c1=90，c2=300

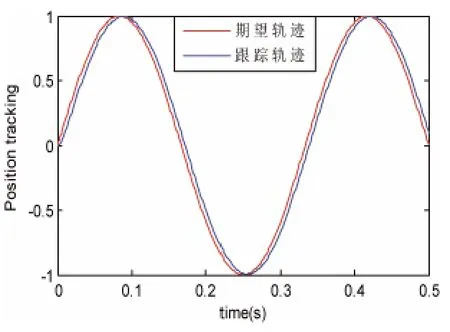
图2 控制律c1=300，c2=300Fig.2 Control law c1=300，c2=300

（1）当控制律c2一定时，随着控制律c1的增大，实际的位置跟踪轨迹无限接近于所期望的轨迹，系统的跟踪性能越好。表明在理想状态下，本文所设计的滑模反演控制器是合适的。

（2）当c1一定时，随着c2的增大，也符合结论1的规律。

取指令信号 Yd=sin(2πt)，F(t)=2sin(t)，Am=-8.4704，Bm=-32.8144；用控制律式（17）取F¯=2，β=1.5；图 3 控制器的控制律取 c1=70，k1=50，h=20。初始状态x(0)=[0 0]。通过MATLAB-SIMULINK进行仿真[12]从而得到的位置轨迹跟踪曲线如图3所示：

（3）取控制器的控制律c1=70，k1=50，h=20得到的位置跟踪轨迹与期望轨迹具有一定的重合度，表明针对有干扰的情况下，所设计的控制器具有良好的跟踪性能。但是由于控制律较多，不能像在理想状态下对控制律进行一定的分析。故只取一对合适的控制律来进行跟踪。

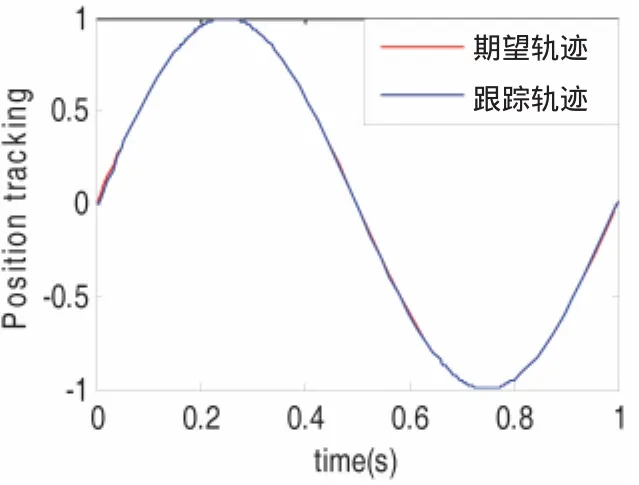
图3 控制律c1=70,k1=50,h=20Fig.3 Control law c1=70,k1=50,h=20

4 结束语

本文针对水下机器人的深度控制进行了一定的分析，在垂直面内建立模型并简化。将系统外界干扰看作为一个广义的外界干扰，使用自适应规则进行上界估计，并在此基础上，从Lyapunov稳定性原理出发，逐步反演设计出滑模变结构控制器。由仿真结果表明，该方案分别在理想和有干扰的情况下设计的滑模控制器具有良好的轨迹跟踪的效果，符合设计的要求。系统的跟踪精度有所提高，并具有更高的鲁棒性。因此，本文在理论上为水下机器人在深度方向的轨迹跟踪控制提供了新的思路。

[1]程婷婷,罗 均,唐智杰,等.自治水下机器人深度的动态Terminal滑模控制的研究[J].机械工程师,2010(9):6-8.

[2]王一云,严卫生,高 剑,等.基于滑模变结构控制滤波的水下机器人水平面轨迹跟踪控制 [J].计算机测量与控制,2013,21(2):382-385.

[3]熊华胜.自治水下机器人深度的鲁棒控制仿真[J].计算机仿真,2007(3):156-159.

[4]HONG E Y,GEOK H,CHITRE M.Depth Control of an Autonomous Underwater Vehicle,STARFISH[J].OCEANS,2010.

[5]ZANOLI S M,CONTE G.Remotely operated vehicle depth control[J].Control Engineering Practice,2003(11):453-459.

[6]BESSA W M,DUTRA M S,KREUZER E.Depth control of remotely operated underwater vehicles using an adaptive fuzzy sliding mode controller[J].Robotics and Autonomous Systems,2008(56):670-677.

[7]SOYLU S,BUCKHAM B J,PODHORODESKI R P.A chattering-free sliding-mode controller for underwater vehicles with fault-tolerant infinity-norm thrust allocation[J].Ocean Engineering,2008(35):1 647-1 659.

[8]YUH J.A Neural Net Controller for Underwater Robotic Vehicles[J].IEEE Journal Engineering,1990,15(3):161-166.

[9]HEALEY A,LIENARD D.Multivariable Sliding mode Control for Autonomous Diving and Steering of Unmanned Underwater Vehicles[J].IEEE Journal of Oceanic Engineering,1993,18(3):327-339.

[10]李殿璞.船舶运动与建模[M].北京:国防工业出版社,2008.

[11]胡传亮.水下机器人动力学建模及定深控制研究[D].武汉:华中科技大学,2007:37-38.

[12]李 颖.Simulink动态系统建模与仿真[M].第2版.西安:西安电子科技大学出版社,2009.

[13]高 剑,徐德民,严卫生.基于自适应反演滑模控制的AUV水平面动力定位方法[J].机械科学与技术,2007(6):738-740.