可变聚类无标度网络上的谣言免疫策略

何郁郁， 邹艳丽， 许旋风， 郑 京

（广西师范大学电子工程学院，广西桂林 541004）

可变聚类无标度网络上的谣言免疫策略

何郁郁， 邹艳丽*， 许旋风， 郑 京

（广西师范大学电子工程学院，广西桂林 541004）

提出一种聚类免疫策略，使用改进的经典谣言传播模型，在可变聚类无标度网络上研究其免疫效果.研究发现，聚类免疫的效果随着网络聚类系数的增加而变好.在不同聚类系数下，比较目标免疫、介数免疫、紧密度免疫和聚类免疫的免疫效果发现，无论网络的聚类特性如何，介数免疫始终是几种免疫策略中效果最好的，当网络聚类系数较大时，聚类免疫的效果超过紧密度免疫接近目标免疫，进一步增大网络的聚类系数，聚类免疫的效果超过目标免疫而接近介数免疫.

聚类系数；免疫；谣言传播模型；可变聚类无标度网络

0 引言

谣言，指的是没有相应事实基础、却被捏造出来并通过一定手段推动传播的言论.当有害的谣言在社会网中传播时，能引起人们的恐慌，给社会带来经济损失.因特网的普及和发展，在给人们带来便利的同时，也加速了谣言的传播.最近网络谣言的传播已给社会秩序带来了严重的影响.因此寻找一种能抑制谣言在社会网中传播的机制，变得越来越重要.

Daley和Kendall［1］于1964年首先提出谣言传播的数学模型（DK模型），而后Maki和Thomson［2］在此基础上提出MT模型.但DK模型和MT模型的缺点是都没有考虑网络的拓扑结构.Zanette［3－4］最早在复杂网络上建立谣言传播模型，并在小世界网络中得出了谣言传播存在临界值的结论.Moerno［5］等人发展了DK模型，同时把由计算机仿真与通过数学分析方法得出的结论进行比较［6］.Anurag Singh［7－8］对Moerno的模型进行修改，将免疫人群进一步分为接受但不传播谣言和拒绝且不传播谣言两类，并以此模型为基础，对小世界网络和无标度网上的随机免疫和目标免疫进行研究.

前人对复杂建模进行了大量研究［9－13］，发现现实世界中许多网络既具有幂律度分布，又具有高聚类性质.而WS小世界网络虽具有高聚类、短平均路径性质，但网络度分布却不服从幂律分布；BA网络虽具有幂律分布，但其网络聚类系数却很低.因此Holme［14］等人提出了一种聚类系数可变的无标度网络模型，该模型可生成同时具有幂律度分布和较高聚类系数的网络.

免疫是控制谣言在网络中传播的有效方法.潘灶烽［15］等人研究了谣言在可变聚类系数无标度网络上的传播过程，发现通过增大网络聚类系数可以有效地抑制谣言传播.受此启发，提出一种新的聚类免疫方法，然后使用改进的SIR模型，在可变聚类系数无标度网络上研究抑制谣言传播的效果.通过改变网络的聚类系数，分析聚类免疫效果与网络聚类特性的关系，并对聚类免疫和其他几种免疫策略的免疫效果进行了比较.

1 网络模型及谣言模型

1.1 可变聚类系数无标度网络模型

研究谣言传播和免疫采用的网络模型是聚类系数可调的无标度网络模型，该模型是Holme等人为了补充小世界网络和无标度网络的不足而提出的.该模型通过对BA网络的生成规则进行修改，可以得到同时具有幂律度分布和较高聚类系数的网络.

可变聚类系数无标度网络的生成法则为：初始时，网络有m0＝m＋1个全连接的节点，之后每个时步网络新增一个与网络有m条连边的新节点i．节点i先采用与BA网络模型相同的优先连接法则，和网络中已存在的节点j做一次优先连接．为了增加网络的聚类，接下来节点i将以概率pt随机地与节点j的邻居做三角连接，如果节点j的所有邻居都已经和节点i相连，那么节点i将会以1－pt的概率做优先连接，直到m条连边都添加完，网络再添加下一个新节点.

通过分析可以发现，可变聚类系数无标度网络的聚类系数主要与三角连接概率pt有关．当概率pt增加时，网络新增节点做三角连接的概率增加，节点邻居互为邻居的概率增大，从而网络整体聚类系数增加.而当pt为0时，可变聚类网络则退化为BA网络.

1.2 谣言传播模型

经典的SIR谣言传播模型是将所有的人群分为三类：无知个体（Ignorants）、传播者（Spreaders）和免疫者（Stiflers）.其中，无知人群是指容易受信息影响的人群，传播者是指散播谣言的人群，而免疫者是指听过谣言但对谣言传播失去兴趣的人群.Anurag Singh等［7］对经典模型进行修改，将免疫者又进一步分为两类：一类是接受谣言但没兴趣传播的人群；另一类是拒绝谣言人群（对谣言不感兴趣不接受，此类可视为传播模型中的免疫人群）.假设网络中共有N个节点，每个节点都可能具有：无知、传播、接收但不传播和拒绝且不传播，这四种状态中的其中一种.谣言传播过程为：当一个传播者与一个处于无知状态的节点相连时，此无知节点可能会以λ的概率变成一个传播者，也可能以α的概率变为一个接受但不传播谣言的免疫者，还可能以δ的概率变为一个拒绝且不传播谣言的免疫者；但一个传播者与一个处于传播状态或免疫状态的节点相连时，那个主动发起谣言传播的节点会以γ的概率变成一个接受但不传播谣言的免疫者．在此，1－δ可以认为是谣言的可信度，δ越大，1－δ越小，表示谣言听起来越不可信，因此无知者拒绝谣言的可能性越大．参数λ、α和δ满足λ＋α＋δ≤1．

定义I（t）、S（t）、Racc（t）和Rrej（t）分别代表在t时刻，无知节点、传播节点、接受但不传播的免疫节点和拒绝且不传播的免疫节点的数量占总人口的比例.显然有I（t）＋S（t）＋Racc（t）＋Rrej（t）＝1．〈k〉表示网络的平均度，此模型的平均场方程为［7］

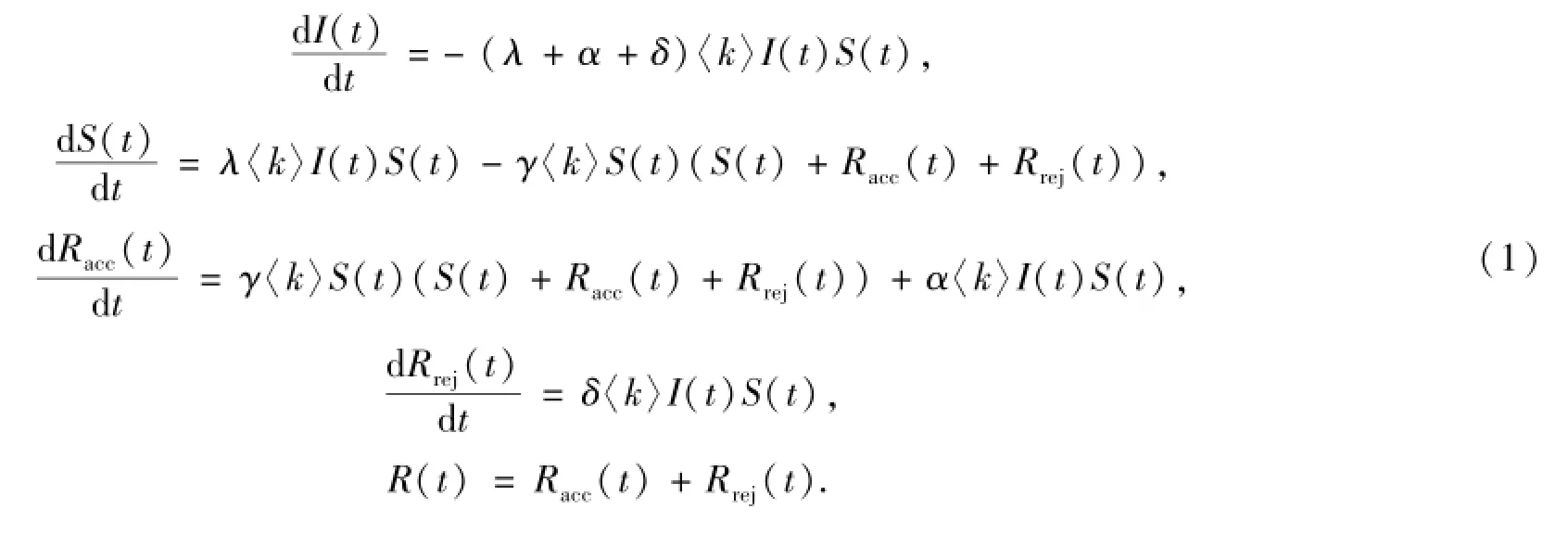
2 免疫策略

免疫是控制谣言在网络中散布的有效方法，而根据网络的特性选择有效免疫策略对于控制谣言的散布可以起到事半功倍的效果.在这里，假设网络规模为N，免疫人口比例为g，则在初始时，网络中有g×N个节点处于免疫状态.

2.1 已有的免疫策略

常用的免疫策略有随机免疫、目标免疫、邻居免疫［16］、节点介数免疫、紧密度免疫等［20］.最近还有学者研究了通过K核分解的方法去寻找网络中最具影响力的节点［17－20］.我们计算发现，研究的可变聚类网络中，应用K核分解方法得到网络中节点的核数值均为m，因此该方法不能区分这类网络中节点的重要性，所以暂不考虑K核免疫.下面介绍本文研究的几种免疫策略.

1）目标免疫 由于在无标度网络中，目标免疫优于邻居免疫、邻居免疫优于随机免疫［8］，所以只研究目标免疫.目标免疫是指对网络中大度节点进行免疫，使用此免疫方法时，需要对网络节点按照度的大小进行降序排列，然后选取排在前面的g×N个节点进行免疫.

2）节点介数免疫 节点介数是指网络中通过该节点的最短路径条数［21］.介数主要用于衡量节点在信息传播中的重要性.节点介数免疫法是先求出网络中每个节点的介数，然后对网络中的节点按照介数的大小进行降序排列，选取排在前面的g×N个节点进行免疫.

3）紧密度免疫 节点i的紧密度定义为该节点到网络中其余N－1个节点的最短路径和的倒数.节点紧密度主要用于刻画节点到其它节点的难易程度［20］.紧密度免疫是指对网络中的节点按照其紧密度大小进行降序排列，选取排在前面的g×N个节点进行免疫.

2.2 聚类免疫

本文主要在可变聚类系数无标度网络上研究谣言的免疫策略.文献［15］的研究表明，增大聚类系数可以有效地抑制谣言传播，由此可见，网络的聚类系数可能和免疫效果之间存在一定的关系，因此，提出一种聚类免疫法.

网络上一个节点的聚类系数是指该节点的邻居间互为邻居的概率.假设网络中的一个节点i有ki个邻居，那么这些邻居间最多可能有ki（ki－1）／2条边，而这ki个节点间实际存在的边数为Ei，那么节点i的聚类系数定义为［21］

聚类免疫策略为：将网络中节点按照聚类系数大小进行降序排列，选取排在前面的g×N个节点进行免疫.

3 仿真实验结果

按照1.1的生成规则生成一个节点个数N＝2 000的可变聚类网络.令网络中的每个节点都处于无知、传播、接受但不传播和拒绝且不传播四种状态中的一种状态，采用1.2节描述的Anurag Singh等提出的谣言传播模型，在t＝0时刻，在网络中随机选择一个节点作为传播者，然后根据不同免疫策略，选择g×N个节点作为免疫节点（状态为拒绝且不传播谣言），剩下的全为无知节点．t＝1时，谣言开始传播，令I（t）、S（t）、Racc（t）和Rrej（t）分别表示在t时刻，无知节点、传播节点、接受但不传播的免疫节点和拒绝且不传播的免疫节点的数量占总人口的比例．谣言模型参数设置为λ＝0.25、α＝0、δ＝0、γ＝0.25．传播结束后，网络中接受但不传播谣言的节点比例Racc（t）是网络5次生成、每次生成100次实验的平均值.

谣言模型中参数α和δ设置为零，是为了避免当传播者与无知者接触时，无知者变成Racc态和Rrej态的情况．当传播过程结束后，网络中Rrej态节点全为初始时的免疫节点；而Racc态节点，则全由传播者与传播者或免疫者接触后变化而成，这时得到的Racc节点比例更能充分体现免疫对谣言传播造成的影响.

3.1 聚类免疫效果和聚类系数的关系

三角连接概率pt取值的大小直接影响网络的聚类系数．当网络初始节点m0＝3，每新增一个节点增加连边数m＝2时，网络平均度〈k〉≈4；当网络初始节点数m0＝7，每新增一个节点增加连边数m＝6时，网络平均度〈k〉≈12．图1分别画出了网络平均度在〈k〉≈4和〈k〉≈12时，不同pt对应的网络聚类系数．由图1可见，在网络连接较稀疏时，改变pt可以在较大范围里调解网络的聚类系数；当网络连接较密时，改变pt，网络的聚类系数变化范围不大.

那么对聚类特性不同的网络，提出的聚类免疫效果会有什么不同呢？图2为网络平均度分别为〈k〉≈4和〈k〉≈12时，采用聚类免疫策略，谣言传播结束后，网络中接受但不传播谣言的节点比例Racc随初始免疫节点比例g的变化.

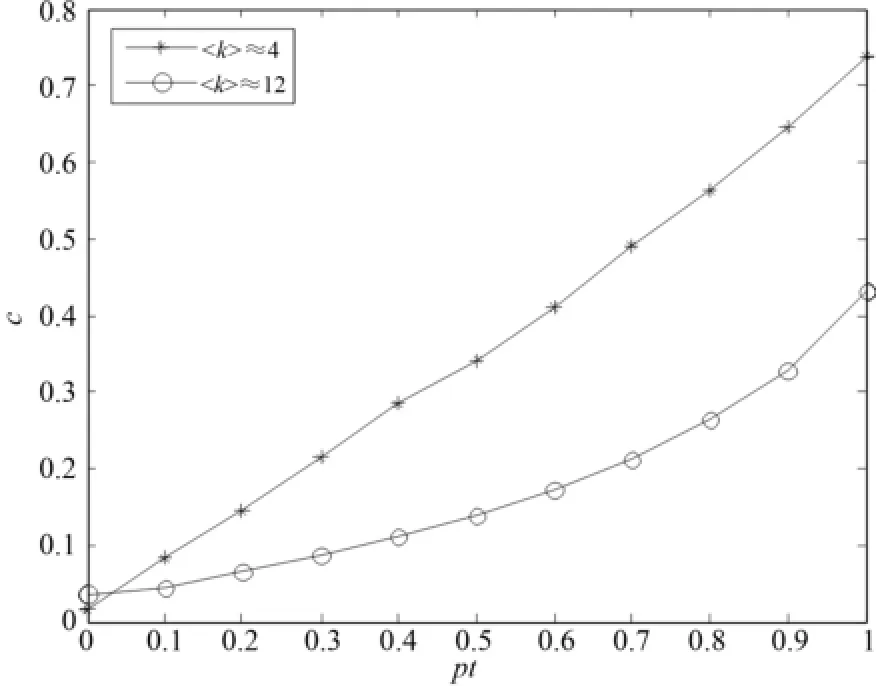
图1 不同三角连接概率下网络聚类系数Fig.1 Network clustering coefficient with different triangle connection probability

图2 不同网络平均度下接受但不传播谣言节点比例Racc随聚类免疫比例g的变化Fig.2 Proportion of Racc Node that accept but do not spread rumors as functions of clustering immune proportion g in networks with different average degree

由图2可知，当网络平均度〈k〉≈4时，聚类免疫效果随网络聚类系数的增加而增强．当pt＝0时，网络聚类系数为0.016 094，聚类免疫临界gc≈0.55；而当pt增大到0.9时，网络聚类系数为0.643 386，聚类免疫临界gc≈0.05，可见在连接较稀疏的可变聚类无标度网络上，聚类免疫临界值随网络聚类系数的增加而减小．但当网络平均度〈k〉≈12时，pt在取值范围［0，0.7］内得到的免疫效果几乎相同，免疫临界值gc≈0.85；而当pt＝0.9时，免疫效果虽有所改善，但免疫临界值也接近0.7.因此当可变聚类网络平均度较小，网络连接较稀疏时，聚类免疫效果随聚类系数增加而增强，免疫有效；当平均度较大时，聚类免疫失效.

3.2 聚类免疫和其它免疫效果比较

由于聚类免疫在连接较稀疏的网络上有效，我们在平均度约为4的可变聚类网络上对聚类免疫、介数免疫、目标免疫和紧密度免疫等几种免疫方法的效果进行比较.我们分别做出了pt取值为0、0.1、0.3、0.5、0.7和0.9时，几种免疫策略的效果图，如图3所示.由图3（a）可见，当pt＝0时，可变聚类网络恢复为BA无标度网络，其聚类系数较小约为0.016，此时聚类免疫效果比其他几种免疫策略效果差；但随着pt的增大，网络聚类系数的增加，聚类免疫的效果变得越来越好，当pt≥0.3时，聚类免疫的效果已经超过紧密度免疫接近目标免疫；当pt≥0.5时，聚类免疫的效果已经超过目标免疫；当pt≥0.7时，聚类免疫的效果已经接近介数免疫；进一步增大聚类系数，我们发现当pt≥0.9时，网络上聚类免疫、目标免疫和介数免疫的效果几乎相同，紧密度免疫效果较差.因此通过在可变聚类系数网络上对几种免疫策略的对比，我们发现无论聚类系数如何，介数免疫始终是最好的，目标免疫次之，当网络聚类特性较强时，可采用聚类免疫.

4 结论

提出一种聚类免疫策略，并使用改进的经典谣言传播模型，在可变聚类系数无标度网络上研究该免疫策略的有效性.研究发现，当网络连接较稀疏、网络平均度较小时，聚类免疫的效果随着网络聚类系数的增加而增强；当网络连接较紧密，网络平均度较大时，聚类免疫失效.接着我们对网络连接较稀疏时，不同聚类系数下，聚类免疫、介数免疫、目标免疫和紧密度免疫这几种免疫策略的效果进行了比较.比较研究发现，无论网络聚类特性如何，介数免疫始终是四种免疫方法中最好的，当聚类系数较大时，聚类免疫的效果超过紧密度免疫和目标免疫而接近介数免疫.因此聚类免疫适用于连接较稀疏，聚类系数较大的无标度网络.本文的研究对于如何在高聚类网络中选择免疫策略，避免谣言大规模传播具有一定的指导意义.

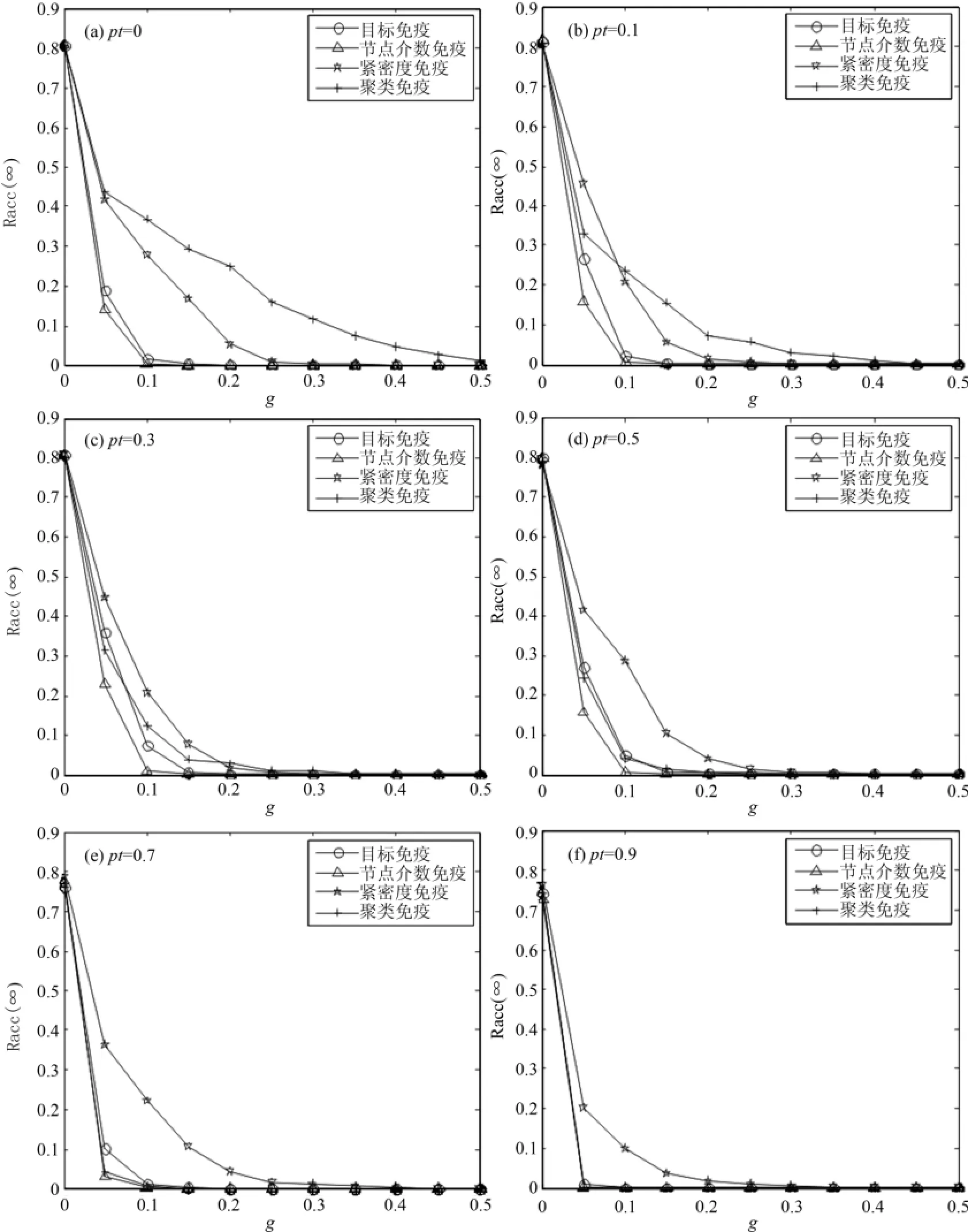
图3 不同网络聚类系数下，几种免疫策略的效果Fig.3 Effects of immunization strategies in networks with different clustering coefficient

［1］ Daley D J，Gani J.Epidemic modelling：An introduction［M］.Cambridge，UK：Cambridge University Press，2001：9－30.

［2］ Maki D P，Thomson M.Mathematical models and applications：With emphasis on the social，life，and management sciences［M］.New Jersey：Prentice—Hall（Englewood Cliffs，N J），1973：23－100.

［3］ Zanette D H.Critical behavior of propagation on small-world networks［J］.Physical Review E，2001，64（5）：1－4.

［4］ Zanette D H.Dynamics of rumor propagation on small-world networks［J］.Physical Review E，2002，65（4）：1－9.

［5］ Moreno Y，Nekovee M，Pacheco A F.Dynamics of rumor spreading in complex networks［J］.Physical Review E，2004，69（6）：1－7.

［6］ 张芳，司广亚，罗批.谣言传播模型研究综述［J］.复杂系统与复杂性科学，2009，6（4）：1－11.

［7］ Singh A，Singh Y N.Rumor spreading and inoculation of nodes in complex networks［C］∥Proceedings of the 21st International Conference Companion on World Wide Web，New York，USA，ACM，2012：675－678.

［8］ Singh A，Kumar R，Singh Y N.Rumor dynamics with acceptability factor and inoculation of nodes in scale free networks［C］∥Eighth International Conference on Signal Image Technology and Internet Based Systems，IEEE，2012：798－804.

［9］ Newman M E J.The structure and function of complex networks［J］.SIAM Review，2003，45（2）：167－256.

［10］ 周涛，柏文洁，汪秉宏，刘之景，严钢.复杂网络研究概述［J］.物理，2005，34（1）：31－36.

［11］ Boccaletti S，Latora V，Moreno Y，Chavez M，Hwang D U.Complex networks：Structure and dynamics［J］.Physics Reports，2006，424（4－5）：175－308.

［12］ Tang Shengxue，Chen Li，Huang Jiaoying.Modeling and identification of associated complex networks［J］.Chinese J Comput Phys，2012，29（2）：308－316.

［13］ Qiao Jian，Fan Ying，Li Guoying.Cause analysis of growing and non-growing scale-free networks［J］.Chinese J Comput Phys，2013，30（2）：309－316.

［14］ Holme P，Kim B J.Growing scale-free networks with tunable clustering［J］.Physical Review E，2002，65（2）：1－4.

［15］ 潘灶烽，汪小帆，李翔.可变聚类系数无标度网络上的谣言传播仿真研究［J］.系统仿真学报，2006，18（8）：2346－2348.

［16］ Cohen R，Havlin S，Avraham D B.Efficient immunization strategies for computer networks and populations［J］.Physical Review Letters，2003，91（24）：1－4.

［17］ Kitsak M，Gallos L K，Havlin S，Liljeros F，Muchnik L，Stanley H E，Makes H A.Identification of influential spreaders in complex networks［J］.Nature Physics，2010，6：888－893.

［18］ Liu J G，Ren Z M，Guo Q.Ranking the spreading influence in complex nerwork［J］.Physica A，2013，392（18）：4154－4159.

［19］ 任卓明，刘建国，邵凤，胡兆龙，郭强.复杂网络中最小K－核节点的传播能力分析［J］.物理学报，2013，62（10）：1－6.

［20］ 胡庆成，尹龑燊，马鹏斐，高旸，张勇，邢春晓.一种新的网络传播中最有影响力的节点发现方法［J］.物理学报，2013，62（14）：1－11.

［21］ 汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.第一版.北京：清华大学出版社，2006：72－97.

Immunity of Rumor on Scale-free Network with Tunable Clustering

HE Yuyu， ZOU Yanli， XU Xuanfeng， ZHENG Jing
（College of Electronic Engineering，Guangxi Normal University，Guilin 541004，China）

We present a cluster immunization strategy and study its immune effect on scale-free network with tunable clustering in a modified classic rumor propagation model.Study shows that effect of cluster immunization becomes better with increasing of network clustering coefficient.Severalimmunizationstrategiesincludingtargetimmunization，betweennessimmunization，closeness immunization and cluster immunization are compared.It shows that betweenness immunization is always the best regardless of network clustering.As a network clustering coefficient is relatively great，effect of cluster immunization is better than that of closeness immunization and close to target immunization.With further increasing network clustering coefficient，cluster immunization exceeds target immunization and approaches to betweenness immunization.

cluster coefficient；immunity；rumor spreading model；scale-free network with tunable clustering

date： 2013－11－15；Revised date： 2014－01－28

TP391

A

2013－11－15；

2014－01－28基金项目：国家自然科学基金（11062001，11165003）资助项目作者简介：何郁郁（1988－），女，硕士生，主要从事复杂网络上的信息传播及免疫策略研究

*通讯作者：邹艳丽（1972－），女，教授，博士，从事复杂网络理论及其应用研究，E-mail：zouyanli72＠163.com

1001-246X（2014）06-0751-06