海南高职院校数学教师专业发展现状——以公办和民办高职院教师为例
杨秀桃,夏 英
(1.海口经济学院基础课部;2.海南工商职业学院基础课部,海南 海口570203)
引 言
为了解海南高职院校数学教师专业发展状况,以及公办与民办学院对数学教师培训投入力度情况,我们选择海南9所高职院校所有一线数学教师进行了问卷调查。本次调查研究目的:了解海南高职院校数学教师专业发展基本状况、数学教师提高业务水平途径、他们对多媒体现代化教学利用及对多媒体需求情况;通过公办与民办学院相关数据列联表分析,试图发现学校性质对其为数学教师提供教学条件、业务培训机会以及参与指导数学建模竞赛机会是否存在明显差异,以便为高职院校数学教师提供良好教学平台提供实证依据。
一 基本情况概述
2013年4月-6月,调查组通过发电子邮件或邮寄问卷方式,发放问卷52份,回收49份,有效问卷49份;公办高职院校发放问卷31份,回收31份,有效问卷31份;民办高职院校发放问卷21份,回收18份,有效问卷18份;问卷调查采用全面调查方式。先通过电子邮件与海南所有11所高职院校数学建模负责人联系,了解一线数学教师人数,再按照份额,通过电子邮件或邮寄方式将问卷调查表发送到相应高职院校。调查表填写均由被调查数学教师在课题组问卷调查指导书指导下完成。调查内容分两部分:被调查者基本情况和教师专业发展内在结构(教育信念、专业能力、专业态度与动机),其中部分问题结果缺失,已在具体问题分析过程中作了说明。
二 统计与分析工具
本文运用统计分析软件 SPSS16.0进行统计、检验、制表及制图。主要采用列联分析方法结合图形分析具体问题[1],同时进行卡方(Chisquare test)检验和输出列联系数指标(Contingency coefficient)。其中卡方检验是用于独立性检验,检验两个类别(行、列)变量之间是否相互独立;列联系数指标用于说明两个类别变量之间相关性程度。卡方检验标准是给定显著性水平值(一般取0.05),当值(卡方统计量概率值)小于值,则表示两个类别变量之间相关性显著;若值大于或等于值,则表示两个变量之间相关不显著,即可认为两个变量相互独立。当两个类别变量相关时,Contingency coefficient系数值越接近1,表示两个类别变量之间相关性越强;越接近0,表示两个类别变量之间相关性越弱(即独立性越强)。
三 调查内容与分析
(一)数学教师基本情况
公办与民办高职院校数学教师基本情况主要包括男女性别分布(见表1)、年龄分布(见表2)、学历分布(见表3)、毕业院校类型分布(见表4)、所学专业分布(见表5)、职称分布(见表6)、工作量情况分布(见表7)等[2]。

表1 男女性别分布状况
表1显示:在海南高职公办学校抽样人数中,男女比例约为1∶1;在海南高职民办学校抽样人数中,男女比例约为1∶2。两者相比,海南民办高职院校女教师比例比公办女教师比例多10.5%。
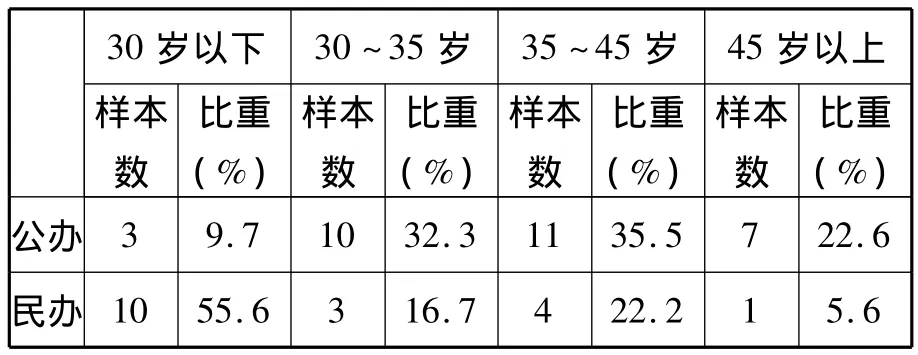
表2 年龄分布状况
表2显示:海南高职公办院校数学教师年龄在35~45岁和45岁以上这两个年龄段者居多,占58.1%;而民办高职院校教师年龄主要集中在35岁以下,占72.3%。公办高职院校30岁以下教师仅占9.7%;而民办高职院校30岁以下教师占 55.6%,多 45.9%。
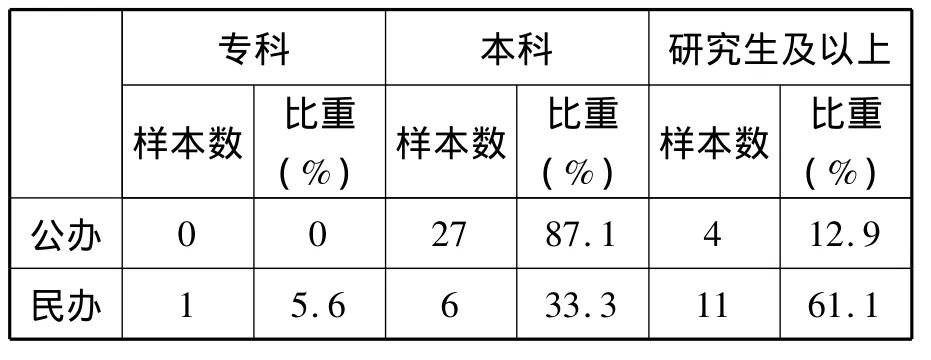
表3 文化程度分布状况
表3显示:海南高职公办院校数学教师学历主要以本科为主,占87.1%,本科生与研究生人数比例为7∶1;而民办高职院校教师学历主要以研究生为主,占61.1%,本科生与研究生人数比例为1∶2。

表4 毕业学校类型分布状况
表4显示:绝大多数数学教师是师范毕业,而工科、综合类院校毕业数学教师偏少,两类学校差别不大。
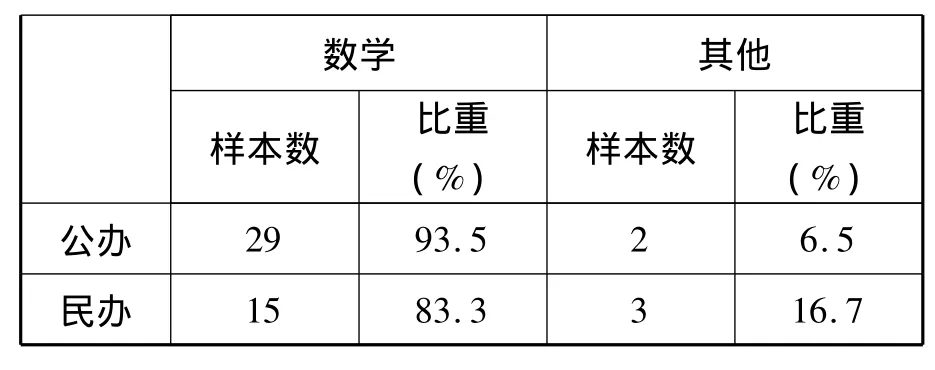
表5 所学专业类型分布状况
表5显示:绝大多数数学教师是学数学专业的,数学专业毕业教师人数比例占对应抽样总数的93.5%和83.3%;而其他专业转行当数学教师者偏少。公办高职院校与民办高职院校相比,转行当数学教师者比例为1∶3。

表6 职称分布状况
表6显示:海南公办高职院校与民办高职院校初、中、高级职称结构比例分别为:3∶14∶14,7∶10∶1;公办高职院校高级职称占近一半,中级职称也占近一半,初级职称者极少;而民办高职院校高级职称仅占5.6%,中级职称以下占94.5%。这表明,公办高职数学教师职称结构比较合理,已形成很好教学梯队;而民办高职数学教师职称结构极不合理,缺乏高职称教师学术带头人。
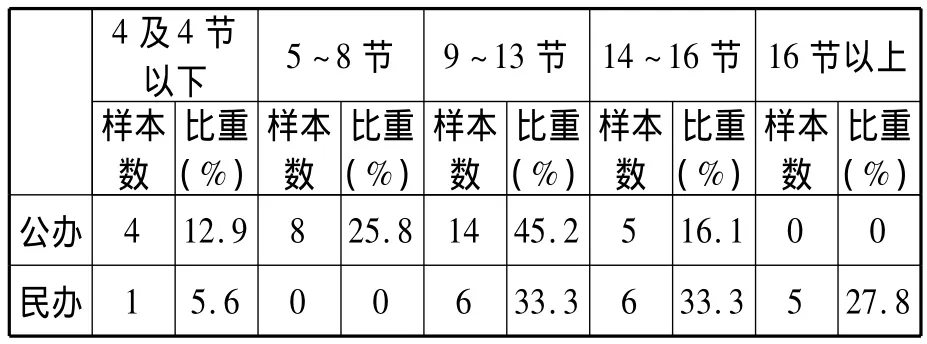
表7 周工作量分布状况
表7显示:海南公办高职院校数学教师周工作量在8节以下者占38.7%,8~12节者占45.2%;而民办高职院校数学教师周工作量在8节以下者占5.6%,8~12节者占33.3%,12节以上者占61.1%。这表明,民办高职数学教师周工作量远高于公办高职数学教师周工作量。
(二)高职数学教师专业发展内在结构
这一部分主要调查海南高职数学教师教育信念、专业能力、专业态度与动机三个方面,设计了12个问题。下面调查数据分析是以学校类型(公办、民办)和所有相关选题进行列联分析,并进行Pearson检验得出是否相互关联的结果。
1.教育信念
在“教育信念”这个环节上,设计了两个体现数学教育观的问题(问题8、9),是为了解高职数学课程地位与作用。
(1)高职数学课程地位
问题8是了解高职数学课程地位,该题下面有“很重要”、“一般”、“重要”、“不清楚”4个选项(列联分析结果见图1)。

图1 高职数学课程地位
图1显示:海南公办、民办高职院校数学教师中,认为数学课程很重要、一般、不重要、不清楚的比例分别为:7∶2∶0∶1,5∶4∶1∶0。这表明,绝大多数高职院校数学教师对自己的教学岗位很重视。公办高职数学教师认为数学课程重要者多近2成,认为不重要者少1成,而定位模糊,不清楚者却高出1成。
理论上,我们假设学校性质与数学课程的高职地位相互独立,通过卡方检验得到:Pearson卡方统计量值,x2=6.832,概率值 p=0.077 >0.05,因此接受该假设,认为学校性质与数学课程的高职地位独立,即没有明显相关性。若考虑显著性水平为 α =0.1,概率值 p=0.077 <0.1,则拒绝该假设,在显著性水平为0.1前提下,认为学校性质与数学课程的高职地位不相互独立,即有较明显相关性。
(2)高职数学课程主要作用
问题9是了解高职数学课程主要作用,该题下面有“训练学生逻辑思维能力(i=1)”、“为学生学习专业知识作准备(i=2)”、“为学生毕业后进一步学习作准备(i=3)”、“培养学生良好的心理素质和思想素质(i=4)”4个选项(列联分析结果见图2)。

图2 高职数学课程主要作用
图2显示:绝大多数教师赞同数学课可以训练学生逻辑思维能力;3成以上数学教师认为数学课程的主要作用是为学生学习专业做准备。公办高职教师中近3成认同数学课为学生毕业后进一步学习做准备;而民办高职教师中2成多认同数学课可培养学生良好心理素质和思想素质。说明民办教师重视学生心理素质培养,而公办教师重视学生未来职业素质培养。
理论上,我们假设学校性质与高职数学课程的主要作用两两独立,通过列联表分析的卡方检验得到[3]:
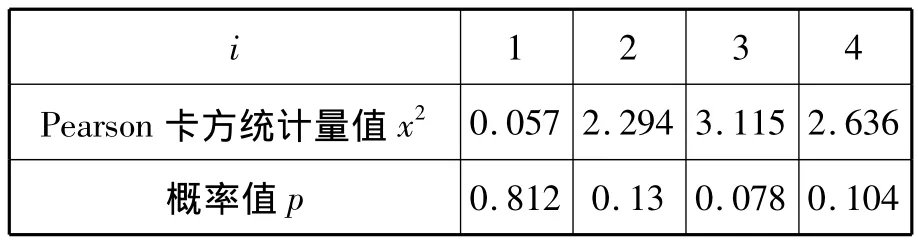
i 1 2 3 4 Pearson卡方统计量值x2 0.057 2.294 3.115 2.636概率值p 0.812 0.13 0.078 0.104
其中的概率值 pi>0.05,(i=1,2,3,4),因此接受该假设,认为学校性质与高职数学课程的主要作用两两独立,即相关性不显著。
2.专业能力
在“专业能力”这个环节上,设计了四个体现应用现代教育技术能力、数学应用能力问题(问题10~15),是为了解高职数学教师专业水平。
(1)采用多媒体辅助教学情况
问题10是为了解高职数学教师多媒体辅助教学情况,有“经常”、“偶尔”、“不用”3个选项(列联分析结果见图3)。
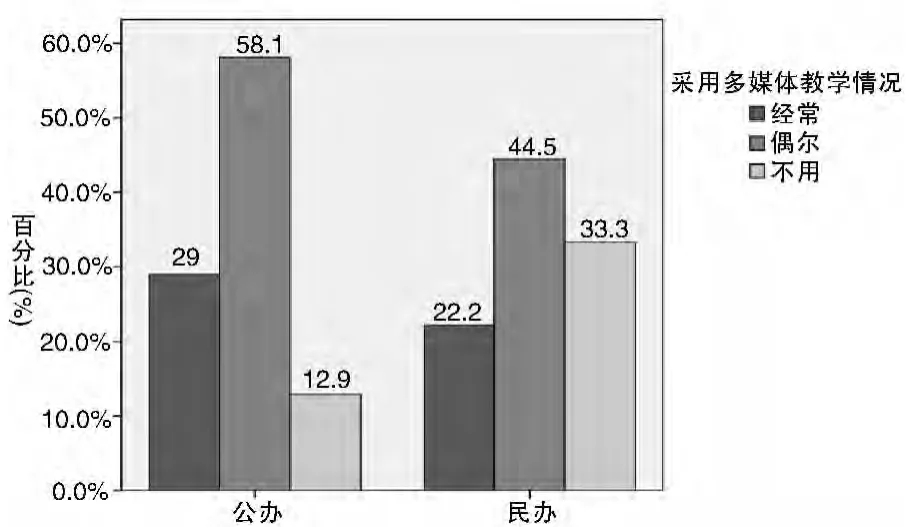
图3 运用多媒体辅助教学情况
图3显示:在采用多媒体教学情况调查中,58.1%公办高职院校数学教师偶尔使用多媒体教学,经常使用者占29%;而民办高职院校数学教师偶尔使用多媒体者占44.4%,经常使用者占22.2%。在不适用者中,民办高职院校数学教师比例比公办教师比例多20.4%。
理论上,我们假设学校性质与多媒体使用情况相互独立,通过卡方检验得到:Pearson卡方统计量值 x2=2.926,概率值 p=0.232 >0。05,因此接受该假设,认为学校性质与多媒体使用情况独立,即没有明显相关性。
(2)不使用多媒体辅助教学原因
问题11是为了解高职数学教师不采用多媒体辅助教学原因,有“本人不会”、“本人会,但学校不能提供多媒体设备”、“数学课程没有必要使用”3个选项。
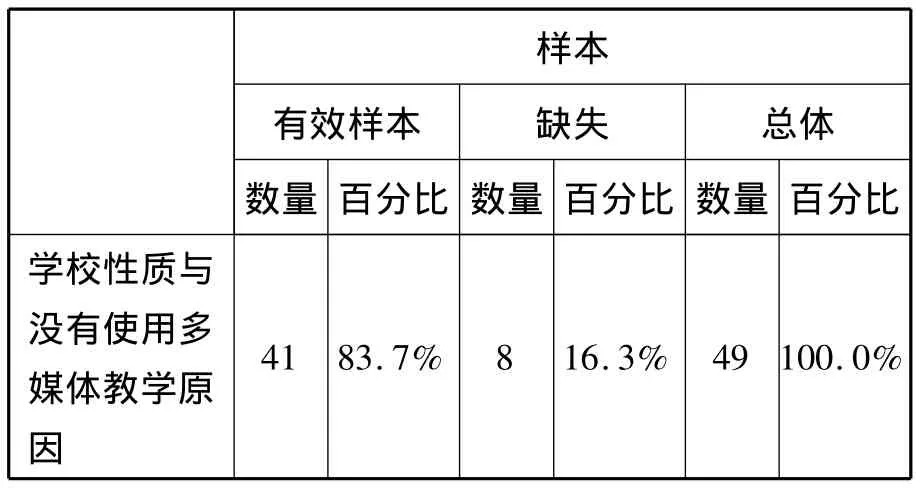
样本有效样本 缺失 总体数量 百分比 数量 百分比 数量 百分比学校性质与没有使用多媒体教学原因41 83.7% 8 16.3% 49 100.0%
说明:在回收问卷中,8份问卷针对不使用多媒体教学这个问题回答缺失。经过剔除缺失样本数据,得到图4中列联分析结果:
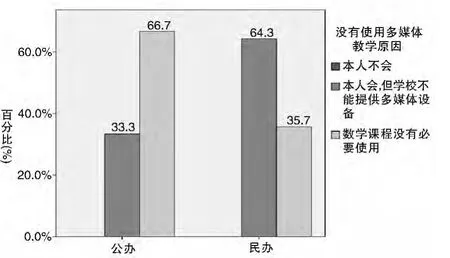
图4 不使用多媒体辅助教学原因
图4显示:在不使用多媒体教学原因调查中,所有高职数学教师都具备多媒体教学基本素养,但由于学校教学条件限制,导致64.3%的民办高职院校数学教师不能使用多媒体进行教学,比公办教师高出近一倍;而公办高职院校数学教师占66.7%,认为数学课程没有必要使用多媒体教学。
理论上,我们假设学校性质与没有使用多媒体教学原因相互独立,通过卡方检验得到:Pearson卡方统计量值x2=3.568,概率值p=0.058>0.05,因此接受该假设,认为学校性质与没有使用多媒体教学原因相互独立,即没有明显相关性。若考虑显著性水平为α=0.1,概率值p=0.058<0.1,则拒绝该假设,在显著性水平为0.1前提下,认为学校性质与没有使用多媒体教学原因不相互独立,即有较明显相关性。
(3)开设数学建模选修课
问卷第2题、第12题是了解调查对象年龄和开设数学建模选修课能力情况(列联分析结果见图5)。
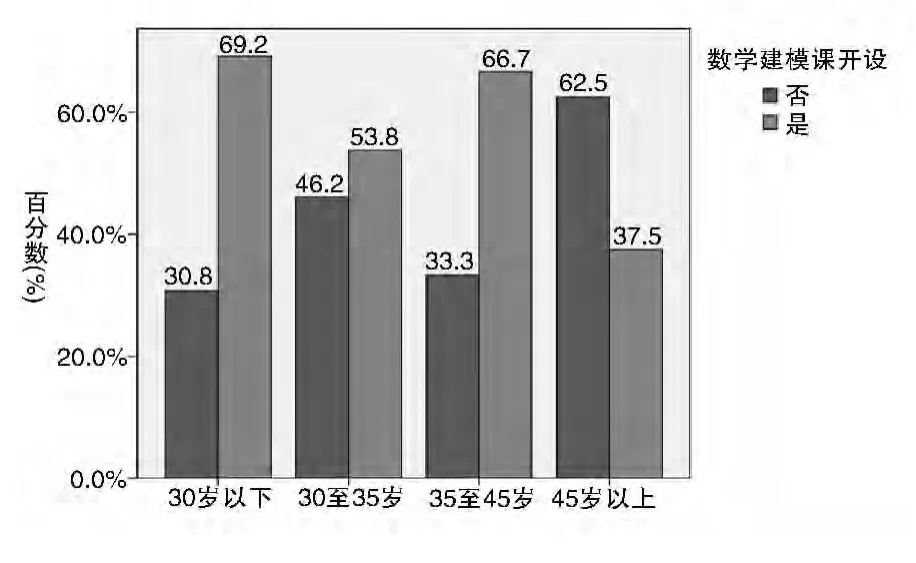
图5 开设数学建模选修课情况
图5显示:开设数学建模课主体是45岁以下教师,45岁以上教师中不开设数学建模选修课者占 62.5%。
理论上,我们假设年龄段与是否开设数学建模选修课相互独立,通过卡方检验得到:Pearson卡方统计量值 x2=2.601,概率值 p=0.457 >0.05,因此接受该假设,认为年龄段与是否开设数学建模选修课相互独立,即没有明显相关性。
(4)未开设数学建模选修课原因
问卷13题是“您开设过数学建模课程吗?如答案为否,原因是什么?”共有“学校未开设数学建模选修课程”、“学校已开设,但本人未学过”、“曾经学过,但开设难度大”3个选项(列联分析结果见图6)。
图6显示:公办高职院校数学教师中75%属于学校开设了数学建模选修课,但本人因未学过,没有参与选修课授课。民办院校中,75%的数学教师曾经学过数学建模课,但因为建模知识涵盖面大,开设难度不小,所以无法参与。

图6 未开设数学建模选修课原因
理论上,我们假设学校类型与没有开设数学建模课原因相互独立,通过卡方检验得到:Pearson卡方统计量值x2=6.731,概率值p=0.035<0.05,因此拒绝该假设,认为学校类型与没有开设数学建模课原因不相互独立,即有显著相关性,列联系数 Contingency Coefficient=0.502。
(5)指导数学建模活动能力
问卷14题调查了被调查对象参与数学建模活动指导次数,分别从学校性质(i=1)、性别(i=2)两个角度切入分析(列联分析结果见表8-1与表8-2)。

表8 -1 不同学校性质参与数学建模活动指导次数
表8-1显示:公办高职院校数学教师中近一半不参与数学建模活动指导,比民办院校数学教师不参与率低37.3%;大部分参与数学教师都指导了2~3次。
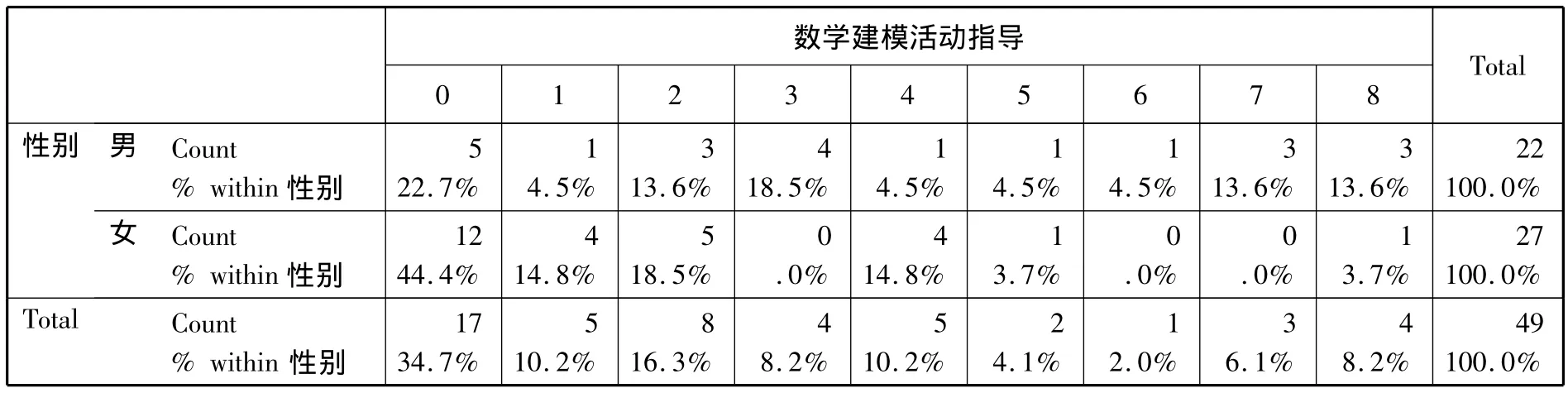
表8 -2 不同性别参与数学建模活动指导次数
表8-2显示:高职院校数学男教师中仅有22.7%不参与数学建模活动指导,而数学女教师不参与率高达44.4%。男教师参与7~8次者达到27.2%,而女教师参与5次以上者仅7.4%。
理论上,我们假设学校性质、教师性别分别与建模能力相互独立,通过列联表分析的卡方检验得到:
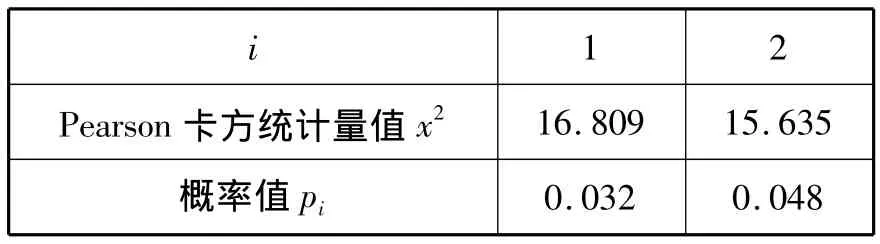
i 1 2 Pearson卡方统计量值x2 16.809 15.635概率值pi 0.032 0.048
其中概率值 pi<0.05,(i=1,2),因此拒绝该假设,认为学校性质、教师性别分别与建模能力相互不独立,即相关性显著,且列联系数Contingency Coefficient分别为:0.505,0.492。
(6)参加数学建模骨干教师培训次数
问卷15题调查了被调查对象参加数学建模骨干教师培训次数(列联分析结果见表9)。

表9 参加数学建模骨干教师培训次数
表9显示:民办高职院校数学教师没有获得培训机会比例为72.2%;公办高职院校数学教师中没有得到参加数学建模骨干教师培训机会为64.5%。公办院校比民办院校得到培训机会高出7.7%,而且公办院校得到多次培训机会比民办院校高出4.1%。
理论上,我们假设学校性质与培训机会相互独立,通过卡方检验得到:Pearson卡方统计量值x2=1.473,概率值 p=0.689 >0.05,因此接受该假设,认为学校性质与培训机会相互独立,即相关性不显著。
3.专业态度与动机
在“专业态度与动机”这个环节,设计了3个问题(问题16~18),是为了解高职数学教师从事数学教学原因、数学教学感受、教学能力自评。
(1)从事数学教学原因
问题16是了解高职数学教师从事数学教学原因,该题有“喜欢数学”、“不喜欢,受专业限制”、“缺数学教师”、“其他”4个选项(列联分析结果见图7)。
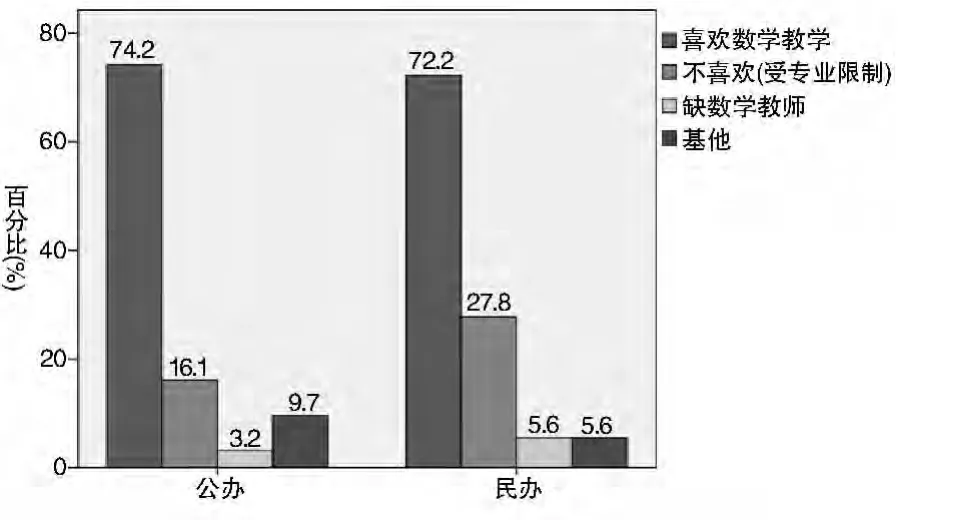
图7 从事数学教学的原因
图7显示:海南高职院校数学教师中,绝大多数教学动机都是喜欢数学教学,两类型学院比例相当。不喜欢数学教学,受到专业限制者,民办院校所占比例比公办院校所占比例多11.7%;这表明,绝大多数数学教师教学动机正确,但仍有近3成教师对目前从事数学教学工作缺乏强烈教学动机。
理论上,我们假设学校性质与从事数学教学工作各原因两两独立,通过列联表分析卡方检验得到:
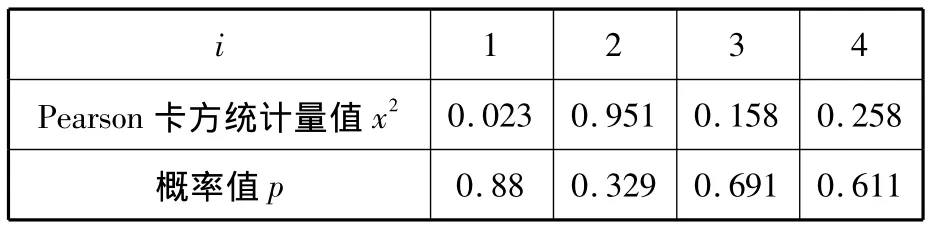
i 1 2 3 4 Pearson卡方统计量值x2 0.023 0.951 0.158 0.258概率值p 0.88 0.329 0.691 0.611
其中概率值 pi>0.05,(i=1,2,3,4),因此接受该假设,认为学校性质与从事数学教学工作各原因两两独立,即相关性不显著。
(2)数学教学感受
问题17是了解高职数学教师从事数学教学的感受,该题有“有成就感”、“有充实感”、“有压力”、“有失落感”、“很无奈”、“其它”6个选项(列联分析结果见图8)。

图8 从事数学教学感受
图8显示:在教师专业态度分析中,有成就感、有充实感者不及1/3,有失落感、很无奈者接近1/3。民办高职院校数学教师失落感、无奈感高于公办高职院校数学教师近1~2成。这说明,高职院校数学教师自我专业认同感不够强烈。
理论上,我们假设学校性质与授课感受两两独立,通过列联表分析卡方检验得到:
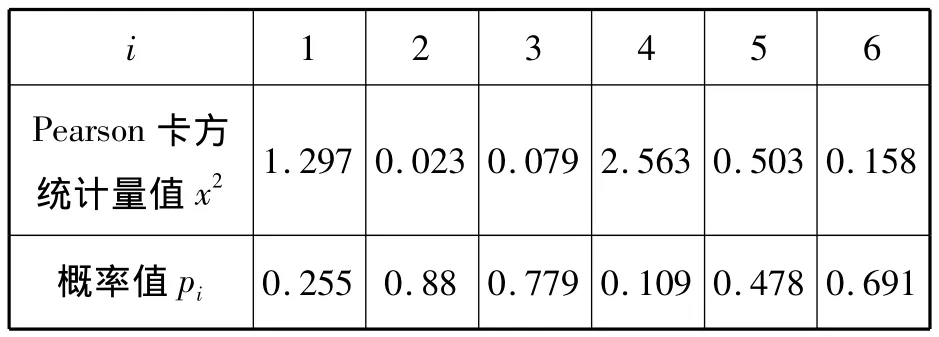
i 1 2 3 4 5 6 Pearson卡方统计量值x2 1.297 0.023 0.079 2.563 0.503 0.158概率值pi 0.255 0.88 0.779 0.109 0.478 0.691
其中概率值 pi>0.05,(i=1,2,…,6),因此接受该假设,认为学校性质与授课感受两两独立,即相关性不显著。
(3)数学教学自评
问题18是了解高职数学教师教学能力自评,该题有“很好”、“较好”、“一般”3个选项(列联分析结果见图9)。

图9 教学能力自评
图9显示:在教学能力自评中,自评很好、较好、一般者占公、民办高职院校数学教师比例分别为:1∶13∶5,1∶6∶3,基本呈现正态分布。民办高职院校数学教师教学自评能力一般者比例高于公办高职院校数学教师近1成。
理论上,我们假设学校性质与教学能力自评相互独立,通过卡方检验得到:Pearson卡方统计量值 x2=0.796,概率值 p=0.672 >0.05,因此接受该假设,认为学校性质与数学教学能力自评相互独立,即没有明显相关性[4]。
四 分析与结论
本次调查一个重要结论是:公办与民办高职院校发展规模虽然有差异,但两个类型在毕业学校类型、所学专业类型、教育信念、从事教学动机与感受、教学能力自评这五方面不存在明显差异。这就意味着数学教师在教学岗位上素养、教学动机、感受与学校性质无关。本次调查结果显示的不同情况有:
(一)在基本概况方面的年龄、学历、职称、周工作量上差别较大。公办高职院校数学教师年龄搭配合理,学历以本科为主,高级职称占主体地位,已形成良好师资梯队,且周工作量在8节以下;民办高职院校数学教师青年教师居多,学历以硕士研究生为主,高级职称较少,无法形成良好教学梯队。
(二)在高职数学教师专业发展内在结构上,不使用多媒体辅助教学原因、未开设数学建模选修课原因、指导数学建模活动能力、参加数学建模骨干教师培训次数等方面差别较大。民办高职院校硬件水平跟不上,师资力量薄弱,培训投入不足,导致民办高职院校没有充足多媒体设备提供给数学教学,同时外出培训机会也很少,导致教师业务水平提升很慢,加上没有良好师资队伍传帮带,所以整体数学教学水平不如公办院校高。
[1]王保进.英文视窗版SPSS与行为科学研究[M].北京:北京大学出版社,2007.
[2]王子舟,方允章.福建村民知识能力及图书馆的利用[M].北京:国家图书馆出版社,2010.
[3]夏怡凡.SPSS统计分析精要与实例详解[M].北京:电子工业出版社,2010.
[4]吴明隆.问卷统计分析实务——SPSS操作与应用[M].重庆:重庆大学出版社,2010.

