一类线性方程组奇异边值问题的谱配置方法

蔡伟云，王天军，殷艳红

（河南科技大学数学与统计学院，河南 洛阳 471023）

一类线性方程组奇异边值问题的谱配置方法

蔡伟云，王天军，殷艳红

（河南科技大学数学与统计学院，河南 洛阳 471023）

对常微分方程组奇异边值问题进行了正则化处理，利用Legendre-Gauss-Lobatto节点为配置点，用Legendre谱配置法求其数值解，逼近方程组的正确解。数值例子说明求解该类问题的具体方法和步骤。数值实验结果证明了所提算法格式的有效性和高精度。

常微分方程组；奇异边值问题；Legendre配点法；Legendre-Gauss-Lobatto节点

0 引言

常微分方程（组）奇异边值问题是在多个科学领域经常出现的一类情况［1－3］。最近，一些作者针对不同类型方程（组）的奇异边值问题提出了不同的数值方法［4－10］。文献［5］给出了单个方程具有正则型奇异点边值问题的谱配置方法。而文献［4］考虑如下方程组奇异边值问题

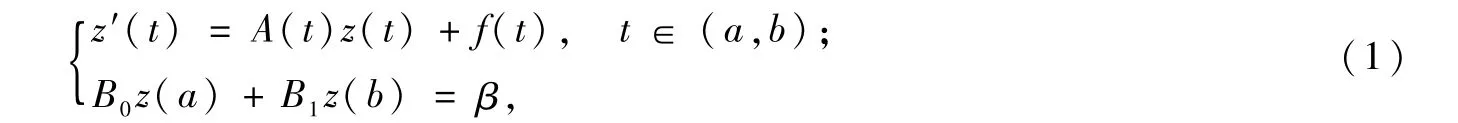
的分段m次插值多项式逼近，其中，z为n维列向量，A（t）为已知n×n矩阵函数，f（t）为已知n维列向量，且可有正则型奇点。然而，目前针对方程组奇异问题的Legendre谱配置法的相关文献鲜见。另一方面，高阶方程可通过降阶方法化为一阶方程组求解。所以，研究方程组的谱配置法是非常有意义的。本文考虑上述模型问题的谱配置法，以期获得高精度的数值解，也为高阶方程的求解提供高精度数值方法。

1 线性方程组奇异边值问题的数值方法

1.1 一阶微分矩阵

记LN（x）（－1≤x≤1）为N次Legendre多项式。x0＝－1；xN＝1；xm（1≤m≤N－1）是N（x）＝0的根［11］。以xi为节点的Lagrange插值基函数为：

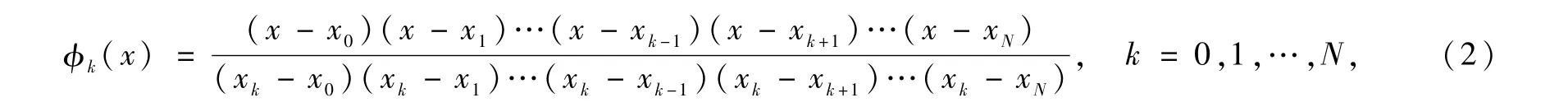
满足：

引理 令D＝（dkj）（N＋1）×（N＋1），称D为一阶微分矩阵。则有［11－13］：

1.2 线性方程组奇异边值问题的算法格式

为方便起见，记∂tz1＝d z1／d t。考虑如下方程组边界奇点情形：

其中，a＝80；k＝16；c＝（a／k）kek；z＝（z1（t），z2（t））T。问题（4）可化为下面等价问题：

为利用Legendre-Gauss-Lobatto节点为配置点求式（5）的数值解，作变换问题（5）化为：

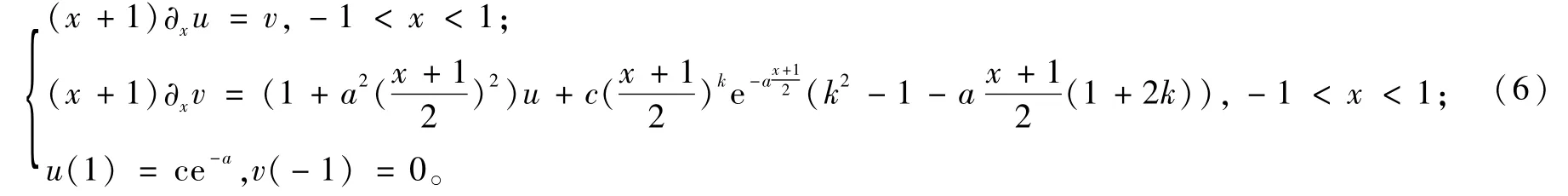
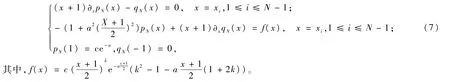
由式（3），式（7）等价的表示为：

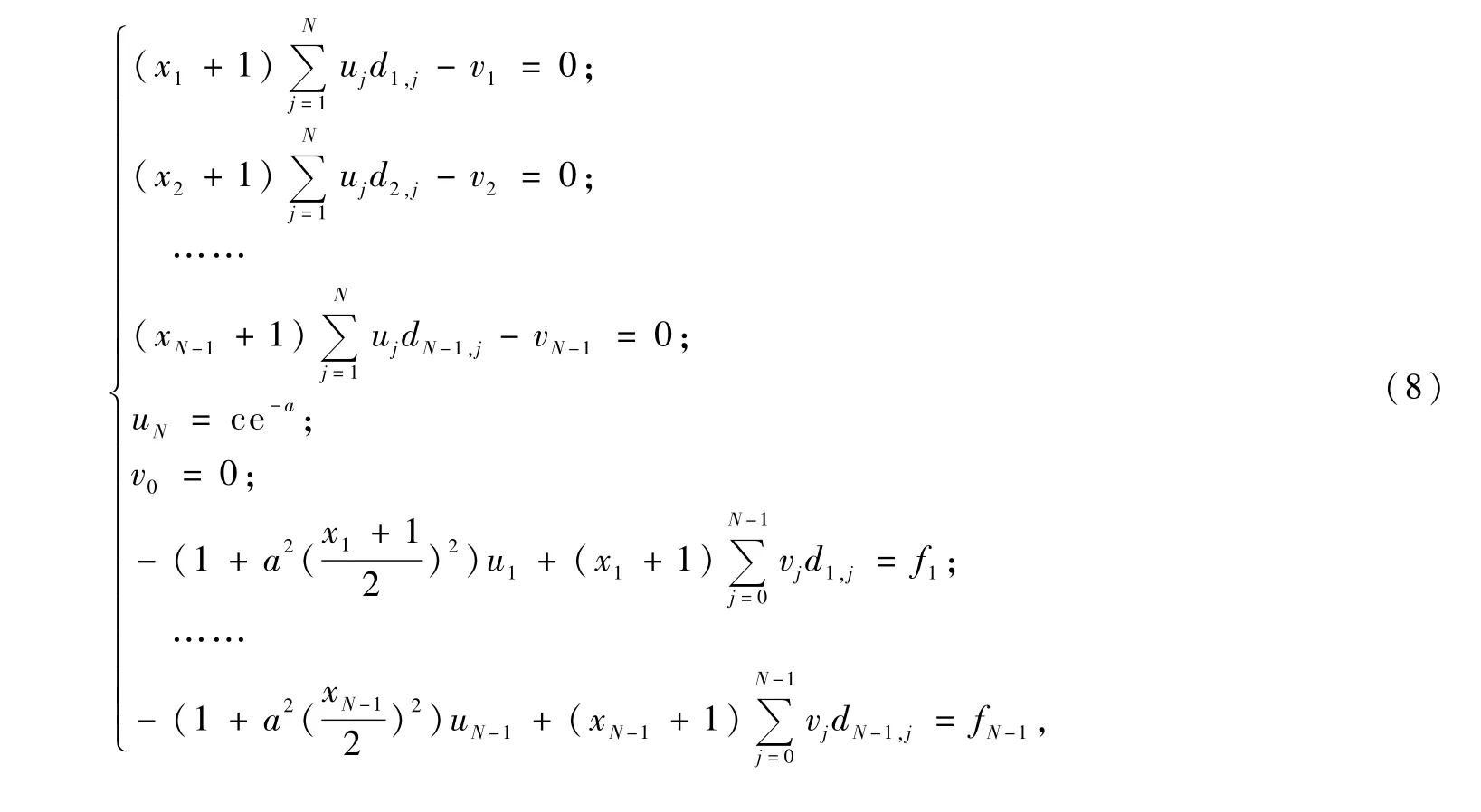
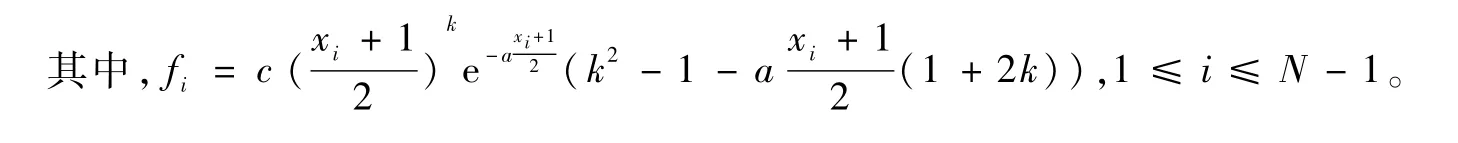
2 数值结果

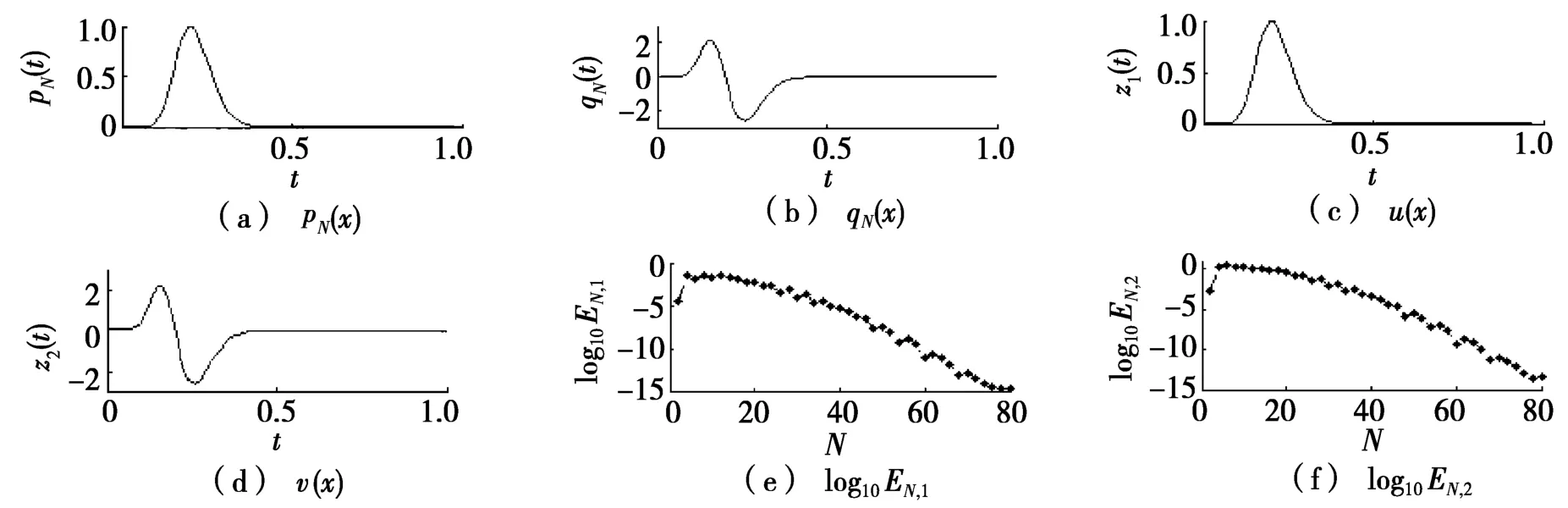
图1 问题（6）的两个分量的近似解、正确解及其数值误差

3 结论

由于p-阶微分算子的条件数为O（N2p）（N为配点个数）［14］，所以，可以将高阶方程通过降阶方法降为一阶微分方程组求解。本文针对一类线性常微分方程组奇异边值问题用Legendre-谱配置方法数值求解，为高阶方程的求解提供方便。比如只需要计算一阶微分矩阵，避免计算高阶微分矩阵，这样就改善了微分矩阵的条件数，在实际计算中节省大量工作，充分体现了所提算法的优势。尽管本文仅考虑了一个线性模型问题，但所用方法与不动点迭代等方法结合，对非线性方程组的求解同样适用。另外，这里所用方法适用于正则型边界奇点情形，对于非正则型奇点的常微分方程组奇异边值问题数值方法有待今后进一步探讨。

［1］ O’Regan D.Theory of Singular Boundary Value Problems［M］.Singapore：World Scientific Press，1994.

［2］ Zhang Y.Positive Solutions of Singular Sub-linear Emden-Fowler Boundary Value Problems［J］.JMath Anal App l，1994，185：215－222.

［3］ Wei Z L.A Class of Fourth Order Singular Boundary Value Problems［J］.Appl Math Comput V，2004，153（3）：865－884.

［4］ 陈誌敏.常微分方程组奇异边值问题的数值方法［J］.湖北工业大学学报，2008，23（4）：81－83.

［5］ 王天军.一类线性奇异边值问题的谱配置方法［J］.河南科技大学学报：自然科学版，2013，34（6）：75－78.

［6］ A lipanah A，Razzaghi M，Dehghan M.The Pseudospectral Legendre Method for a Class of Singular Boundary Value Problems Arising in Physiology［J］.Journal of Vibration and Control，2010，16（1）：3－10.

［7］ Temsah R S.Spectral for Some Singularly Perturbed Third Order Ordinary Differential Equations［J］.Numer Algor，2008，47：63－80.

［8］ 阮宗利，李维国.一类线性奇异边值问题的区间分段求解［J］.科学技术与工程，2010，10（20）：4896－4899.

［9］ Knmar M.A Second Order Spline Finite Difference Method for Singular Two Point Boundary Value Problems［J］.Appl Math and Comput，2003，142：283－290.

［10］ Ravi A S V，Reddy K Y N.The Method of Inner Boundary Condition for Singular Boundary Value Problems［J］.Appl Math and Comput，2003，139：429－436.

［11］ Shen J，Tang T，Wang L L.Spectral Methods：A lgorithms，Analysis and Applications［M］.Berlin Heidelberg：Springer-Verlag，2011.

［12］ 王天军，殷政伟.Legendre-Gauss-Lobatto节点的一个注记［J］.河南科技大学学报：自然科学版，2012，33（1）：71－74.

［13］ Yin Y H，Sun A，Wang T J.Spectral Collocation Methods for a Class Of Nonlinear Singular Boundary Value Problems［C］／／Proceedings of the 2013 International Conference on Advanced Mechatronic Systems.Luoyang，2013.

［14］ Wang L L，M ichael D S，Zhao X D.AWell-conditioned Collocation Method Using Pseudospectral Integeration Matrix［J］. Numerical Analysis，2013，arXiv：1305.2041.

O241.81

A

1672－6871（2014）05－0087－03

国家自然科学基金项目（11371123，11171227）；河南省教育厅自然科学基金项目（14B11021）；河南科技大学博士基金项目（09001263）

蔡伟云（1982－），女，河南荥阳人，硕士生；王天军（1963－），男，河南息县人，副教授，博士，硕士生导师，研究方向为偏微分方程数值解.

2014－03－21