一种新的混沌图像加密算法设计

韩双霜，闵乐泉，韩丹丹

（1.北京科技大学a.自动化学院；b.数理学院，北京 100083；2.武警北京指挥学院信息管理中心，北京 100012）

一种新的混沌图像加密算法设计

韩双霜1a，2，闵乐泉1a，1b，韩丹丹1a

（1.北京科技大学a.自动化学院；b.数理学院，北京 100083；2.武警北京指挥学院信息管理中心，北京 100012）

基于修正版的Marotto定理提出了一种新的2维离散混沌映射。通过一个实数域到整数域的变换将该映射产生的混沌流转换成二进制伪随机序列。在此基础上结合二维非等长Arnold变换设计了数字图像加密算法，该算法具有类似一次一密的功能。对该算法的密钥空间、密钥敏感性、统计特性和抗干扰能力进行仿真分析。研究结果表明：该加密算法可以达到较好的加解密效果，可以满足商业网络安全通讯的需求。

Marotto定理；图像加密；非等长Arnold变换

0 引言

随着计算机和网络技术的发展，图像信息成为人们进行信息交流的重要手段，如何安全地传送图像信息成为一个迫切需要解决的问题［1］。常用的图像加密算法主要有像素空间位置置乱、图像灰度变换以及两者相结合的方法。较常用的置乱算法包括Arnold变换、幻方变换、Hilbert变换、Gray码变换和亚仿射变换等［2－5］。其中，Arnold变换由于简单且具有周期性的优点，在图像加密中得到了广泛应用。但它仅适合正方形图像的置乱。针对这一不足，文献［6］提出了适用高宽不等图像置乱的二维不等长Arnold变换。

混沌作为一种特有的非线性动力学现象，具有良好的伪随机特性、轨道的不可预测性以及对初始状态极端敏感性。混沌密码学为信息安全保障提供了新的工具。目前，应用于图像加密中的离散混沌系统主要是采用对常见系统进行扩展、改进或复合［7－9］，直接利用混沌判据构造新混沌的比较少。本文基于史玉明和陈光荣提出的修正版Marotto定理［10］构造了一个新的二维离散混沌映射，在此基础上结合二维非等长Arnold变换设计了一个数字图像加密算法，能够对灰度图像成功加密且实现了无失真解密。相关的安全性分析和仿真实验表明：该加密算法安全性较高，可满足商业网络安全通讯的需求。

1 预备知识

在本节中先介绍一下修正版的Marotto定理，以便于后面的证明。

定理1［10］设z∈ℝn为映射f：ℝn→ℝn的一个不动点。假设：

（Ⅰ）f在z的某领域内连续可微且Df（z）的所有特征值之绝对值大于1，从而存在一个正常数r和ℝn的一个范数，使得f在之下在上扩张，其中

（Ⅱ）z是f的返回扩张不动点，即存在点x0∈Br（z）及正整数m，使fm（x0）＝z，（x0≠z），其中，Br（z）是空间以z为中心的闭球；是空间以z为中心的开球，且f在x0，x1，…，xm－1的某邻域内连续可微且满足det Df（xj）≠0（0≤j≤m－1），其中，xj＝f（xj－1），0≤j≤m－1。

则系统在Li-Yorke意义下是混沌的。

2 图像加密算法

2.1 新二维离散混沌映射

基于定理1，本文构造了一个新的二维离散映射，

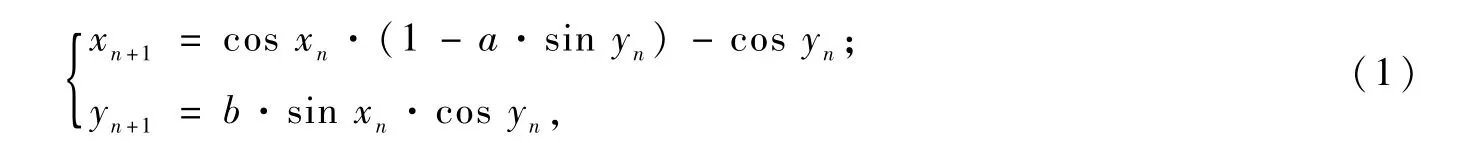
其中，参数分别为a＝3，b＝5。下面证明该映射是混沌映射。

证明可以看出z＝（0，0）T为该离散映射的一个不动点，且对于一个r0＞0，映射（1）在Br0（z）上连续可微，对任一点X＝（xn，yn）T其Jacobi矩阵的表达式为：

代入z得到两个特征值λ1，2＝±3.873i，即所有特征值的绝对值均大于1，满足定理1中的（1）。

下面证明f在Br（z）内有返回扩张不动点。设存在正整数m＝2及一点x0＝（x，y）T使得f2（x0）＝0，x1＝f（x0）≠0。即

综上所述该映射满足定理1，即映射在Li-Yorke意义下是混沌的。证毕。

在a＝3，b＝5，x0＝0.5，y0＝0.1时能产生混沌轨道，其迭代轨迹如图1所示。

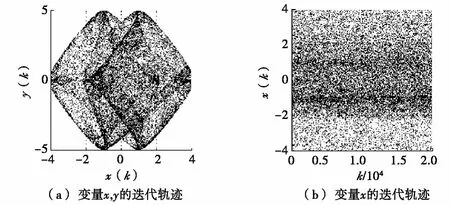
图1 混沌映射的迭代轨迹

2.2 算法描述

设要加密的图像为I＝｛I（i，j）｝，其中I（i，j）为空间坐标（i，j）处的像素灰度值，图像大小为m×n，设定一个可逆变换A，该算法中的密钥集为加密方案中的参数为m1，n1，a1， a2，该加密算法的框架如图2所示。下面将详细描述该算法实现过程。

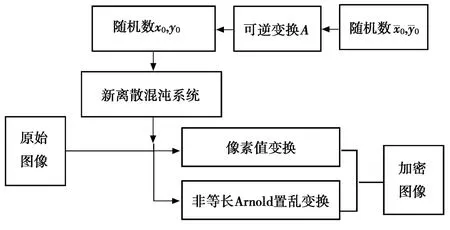
图2 加密算法框架

2.2.1 置乱变换

步骤1：选取A为可逆矩阵

步骤2：以x0，y0作为初始条件，利用系统（1）迭代一定次数后生成混沌序列｛x（k），

步骤3：将图像进行2×2分块，得到P1，P2，P3，P4（编号按行优先的顺序编排，如图3所示）。

步骤4：以其中的图像子块P1为例，其图像大小为m1×n1。选取迭代第m1次后得到的序列x（m1）、y（m1）和常数a1、a2做处理产生b1和r1，其中，b1＝abs（round（x（m1）×a1）），r1＝abs（round（y（m1）×a2））。利用二维非等长Arnold置换k1次得到P′1。其余子块按类似方法置乱，得到P′2，P′3，P′4。

图3 图像分块示意图

步骤5：将图像P′1，P′2，P′3，P′4拼合后按步骤4中的方法再进行一次置乱后，得到密文图像I′。

2.2.2 像素值变换

利用表达式I′b（i，j）＝t（i，j）⊕I′（i，j）完成像素值变换，其中，I′（i，j）为密文图像I′的灰度值，t（i，j）是由系统（1）在步骤（2）中产生的混沌序列，经过一个实数域到整数域的变换得到，其中，X（k）＝k1x（k）＋k2y（k），K1＝

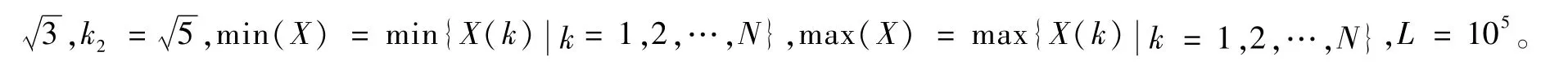
2.3 仿真分析

3 算法的安全性分析

3.1 密钥敏感性分析

为了使图像能抵抗差分攻击，加密图像必须对密钥敏感性较高。数值模拟显示，本算法对密钥集中的9个参数的敏感程度均达到10－15，即攻击者对密钥的尝试攻击即使密钥值有10－15的微扰，想破解原图像也几乎不可能成功。图5a为原图像，图5b～图5 f为密钥集中选取5个密钥分别进行10－15的微扰时所得的解密图像，从中识别不出原图像。

图4 加密方案仿真图

图5 错误密钥解密图

3.2 密钥空间分析

为抵抗穷举攻击，图像加密方案的密钥空间应尽可能的大。通过对密钥密感性测试的数值模拟表明，本算法对密钥集中的9个密钥来说，密钥空间已经达到10235＞2448。若将算法中所涉及的其他一些常数设计为密钥，则密钥空间可进一步增大。

3.3 统计分析

3.3.1 统计直方图

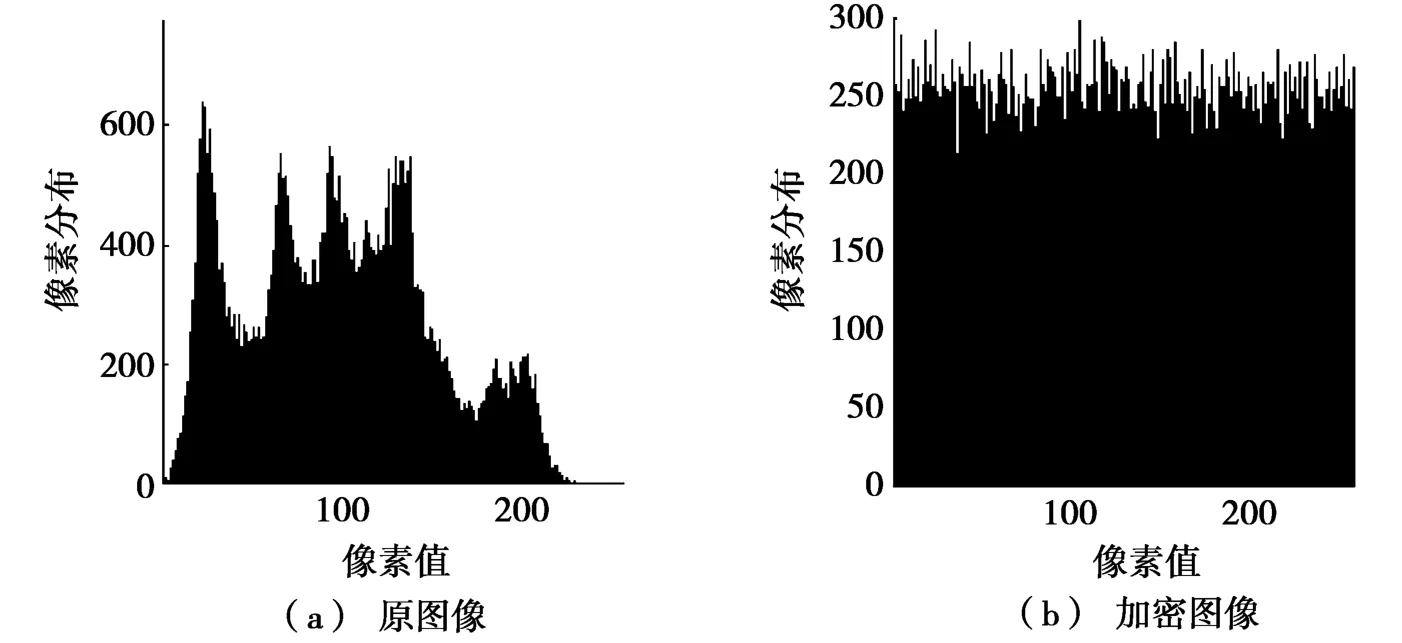
图6 直方图分析

图6a和图6b分别为原图像及加密图像的统计直方图，横坐标代表256个灰度级，纵坐标代表所有像素取每个灰度级的频数。由图6可以看出：两者有很大区别，并且加密图像的直方图分布的比原图像均匀，概率分布接近等概率分布，增加了破译的难度。

3.3.2 相邻像素的相关性

图7为对角方向原始图像和加密后图像相邻像素的相关关系。由图7可看出：原始图像像素间的相关性呈线性结构关系，而加密后图像像素间的相关性呈随机的对应关系。计算原图像和加密图像像素间的相关系数也可发现：原图的相邻像素高度相关，而加密后图像相邻相关系数接近为零，已基本不相关。

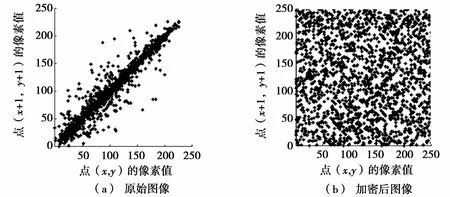
图7 对角方向相邻像素相关性

4 结论

本文基于修正版的Marotto定理，构造了一个新的二维混沌映射。在此基础上结合二维非等长Arnold变换设计了一个数字图像加密方案。仿真结果表明：该算法可以实现对灰度图像的加解密，并且有较好的效果。对算法的安全性分析表明：该算法密钥空间大、密钥敏感性高且统计特性较好。下一步的工作重点将放在对加密算法进行优化，尤其是由控制密钥来进行图像分块的实现以及提高抗干扰能力上。

［1］ 孙燮华.数学图像处理原理与算法［M］.北京：机械工业出版社，2010：35－40.

［2］Deng X P，Zhao D M.Color Component 3D Arnold Transform for Polychromatic Pattern Recognition［J］.Optics Communications，2011，284（24）：5623－5629.

［3］ Yen E，Lin L H.Rubik’s Cube Watermark Technology for Grayscale Images［J］.Expert Systems with Applications，2010，37（6）：4033－4039.

［4］ Joshi M，Shakher C，Singh K.Image Encryption Using Radial Hilbert Transform Filter Bank as an Additional Key in the Modified Double Random Fractional Fourier Encoding Architecture［J］.Optics and Lasers in Engineering，2010，48（5）：605－615.

［5］ 卢斌，王冰.基于改进亚仿射变换的图像信息隐藏算法［J］.计算机工程，2011，37（11）：164－166.

［6］ 邵利平，覃征，高洪江，等.二维非等长图像置乱变换［J］.电子学报，2007，35（7）：1290－1294.

［7］ Kanso A，Ghebleh M.A Novel Image Encryption Algorithm Based on a 3D Chaotic Map［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17（7）：2943－2959.

［8］ Wu Y，Noonan J P，Yang G L，et al.Image Encryption Using the Two-dimensional Logistic Chaotic Map［J］.Journal of Electronic Imaging，2012，21（1）：013014.

［9］ Wang X，Teng L，Qin X.A Novel Color Image Encryption Algorithm Based on Chaos［J］.Signal Processing，2012，92（4）：1101－1108.

［10］ Shi Y M，Chen G R.Discrete Chaos in Banach Spaces［J］.Science in China，Series A：Mathematics，Physics，Astronomy，2005，48（2）：222－238.

TN918

A

1672－6871（2014）05－0037－05

国家自然科学基金项目（61074192，61170037）

韩双霜（1982－），女，安徽颍上人，博士生；闵乐泉（1951－），男，北京人，教授，博士，博士生导师，主要研究方向为住处安全、图像处理.

2013－05－14