Black-Scholes定价模型

李培峦，张增援

（河南科技大学数学与统计学院，河南 洛阳 471023）

Black-Scholes定价模型

李培峦，张增援

（河南科技大学数学与统计学院，河南 洛阳 471023）

研究连续时间衍生品的定价，建立Black-Scholes定价模型，给出了Black-Scholes微分方程的推导过程以及基于鞅方法的Black-Scholes公式。结合欧式期权的定价公式给出了避险参数的表达式及意义。

金融衍生工具；Black-Scholes模型；欧式期权；避险参数

0 引言

随着全球经济的发展，金融衍生工具的品种日益复杂和多样化，加上衍生工具的高风险性，通过模型研究衍生工具显得尤为重要。1973年，Fischer Black和Myron Scholes利用无风险投资理论和随机微分方程理论，得到了著名的Black-Scholes随机偏微分方程［1］，并利用相应的边界条件和概率方法得到了欧式看涨（跌）期权价格的计算公式。Black-Scholes方程的推导方法是定义期权价格的基础，相关的方法较多［2－3］，大部分都是用布朗运动入手，结合偏微分方程的边值理论，但过程较复杂，本文完全采用偏微分方程的理论来推导Black-Scholes方程，过程较简单，并推导了基于鞅方法的Black-Scholes公式，还结合欧式期权的定价公式介绍避险参数的表达式及意义。

Black-Scholes方程是一个连续时间衍生品的定价模型。为了从偏微分方程入手讨论Black-Scholes定价公式，首先要对市场做如下假设：

（Ⅰ）基础资产不支付红利，且其价格服从几何布朗运动，即基础资产（以下均假设基础资产为股票）的价格满足随机微分方程：

其中，μ、σ为常数。

（Ⅱ）市场是完全的、无套利的；可以无限制的卖空；市场无摩擦，即无税收成本、无交易成本。

（Ⅲ）无风险利率是一个常数，且任何期限的借贷利率都相等。

（Ⅳ）基础资产可以以任何数量在任何连续的时间交易。

在这些假设条件下，可以推导出衍生品价格满足的偏微分方程的Black-Scholes微分方程，结合边界条件可以求出衍生品的价格。

1 Black-Scholes微分方程的推导

引理1［2－3］令f（t，St）是关于t和随机过程St的二次可微函数，d St＝αtd t＋σtd Wt（t≥0），漂移项αt和扩散项σt都有很好的性质。则

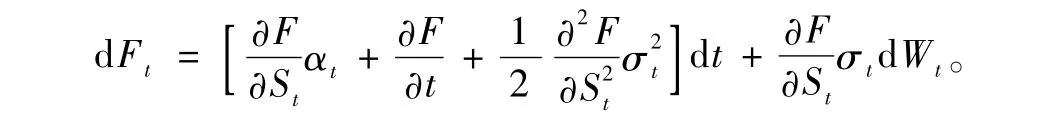
证明下面给出Black-Scholes微分方程的完全利用偏微分理论的推导过程。

用T表示衍生品的期限，f（t，St）表示衍生品t时刻的价格。假设函数f（·，·）具有连续的二阶偏导数，由Itô引理可得：

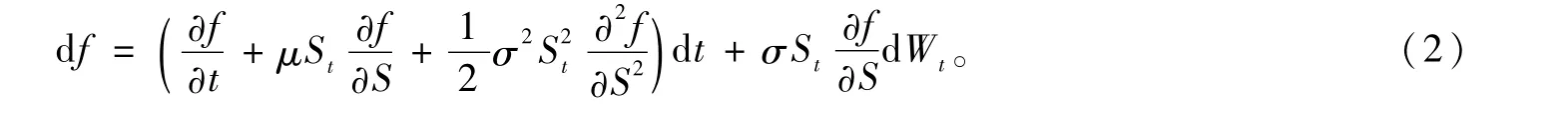
由式（1）和式（2）可以构建一个无风险组合π以消去d Wt项。假设持有－1单位的衍生品单位的股票，则t时刻组合π的价格为：

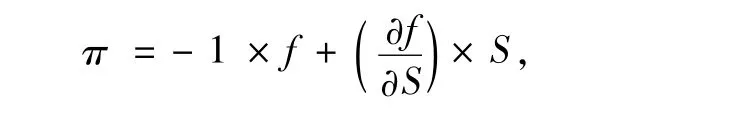
两边求微分可得：

将式（1）和式（2）代入式（3）可得：

整理可得：

从式（4）可以看到：组合π价格的变化仅与时间有关，与市场的状态无关，因此π是无风险组合。故

由式（4）和式（5）可得：

整理可得：

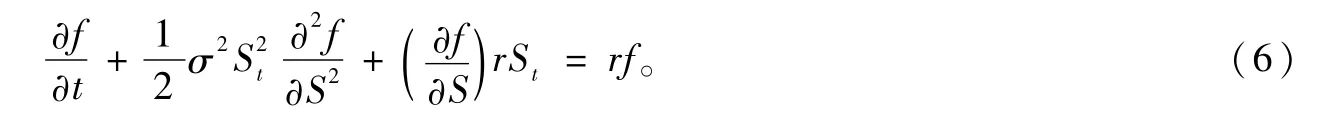
等式（6）就是Black-Scholes微分方程。

基于Black-Scholes微分方程的推导过程，可以得到以下两个推论：

推论1式（1）中的μ和σ可以度量股票的收益和风险。

证明将式（1）差分，得到：

其中，△St＝St＋△t－St；△Wt＝Wt＋△t－Wt。因△Wt～N（0，△t），所以基于t时刻的信息集F Ft对式（7）两边求条件期望可得所以，μ的含义是股票的连续收益率。同理，求△St基于F Ft的条件方差可得所以，σ的含义是收益率的（瞬时）标准差。故μ和σ分别度量了股票的收益和风险。

推论2欧式看涨期权满足的边界条件为：f（T，ST）＝max｛ST－K，0｝，解Black-Scholes微分方程就得到标准欧式期权的价格：

例1 一个1年期欧式看涨期权，其标的资产为一只公开交易的普通股票，已知：a.股票现价为122元；b.股票年收益标准差为0.2；c.ln（股票现价／执行价现价）＝0.2。利用Black-Scholes期权定价公式计算该期权的价格。

解 利用Black-Scholes期权定价公式可得：

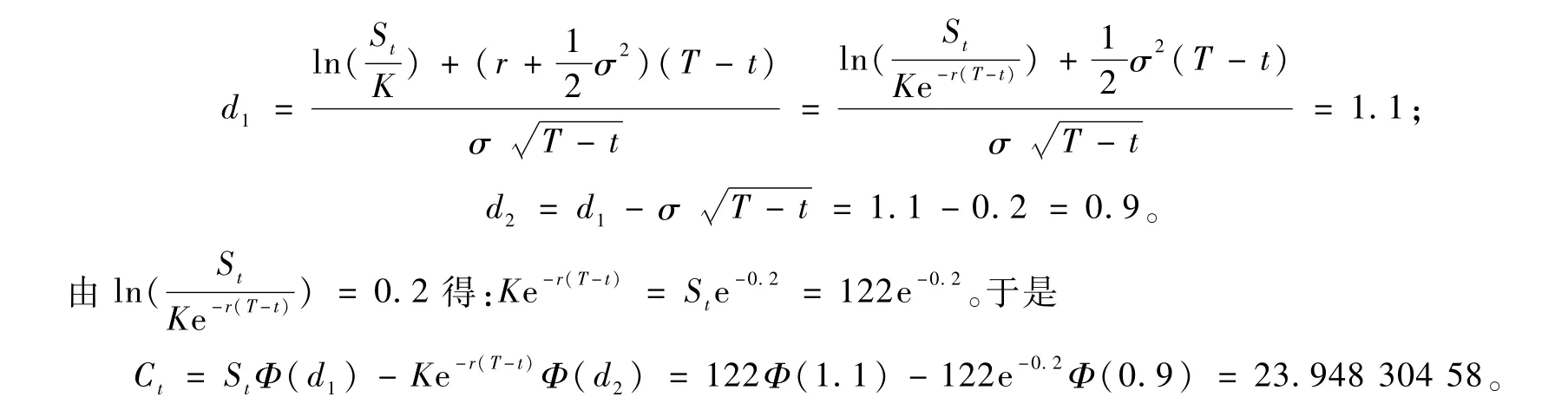
从Black-Scholes微分方程及其推导过程，还可以知道组合π是动态的。由π的定义可以看出：π的价格是随时间变化的，组合中的系数也是随时间变化的，这表明套期保值［4－5］是一个动态的过程。

假设式（1）只涉及一个d Wt项，这表明市场是由一个布朗运动驱动的，也就是说市场只有一个“风险源”。如果衍生品设计多个风险，如随机利率的股票期权的定价中涉及到两个风险，需要用d W1t和d W2t描述其对价格的影响。这样的模型称为双因素模型。衍生品价格满足的微分方程的推导中将用到二维的Itô引理，但推导的思路与单因素的情形相同。

如果基础资产支付红利，其价格满足的随机微分方程变为：

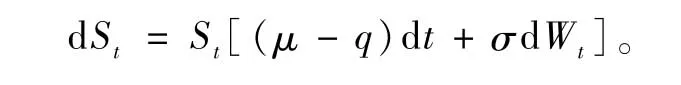
与式（6）的推导类似，可以推导出衍生品价格满足的微分方程：

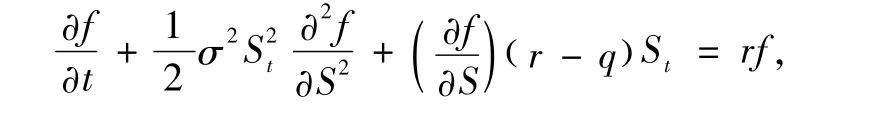
其中，q为股票的红利率。

2 基于鞅方法的Black-Scholes公式

随机偏微分方程的求解非常麻烦，有时甚至根本求不出具体的解，所以需要考虑一种简单的方法求解衍生品的定价公式，下面给出基于鞅方法的Black-Scholes公式。

定理1 在Black-Scholes模型的假设下，市场存在唯一的风险中性概率测度Q，且T时刻到期的衍生品在t时刻的价格可以表示为：

其中，XT为在衍生品到期时的支付额。

证明 建立贴现的基础资产价格过程：

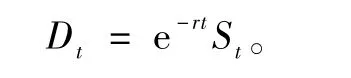
通过Girsanov定理［6］，找到风险中性概率测度Q，使得Dt是一个Q鞅。通过求解式（1）可得客观概率测度下：

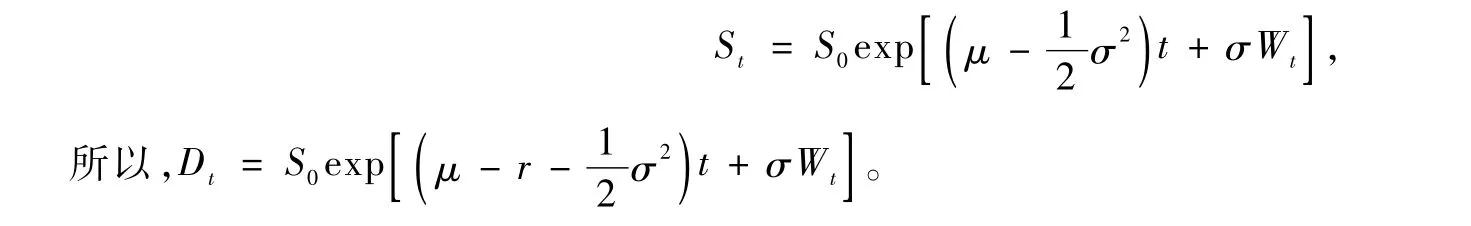
由Girsanov定理，可以找到概率测度Q，使得：

定义过程Vt和Et由条件期望的塔性质［7］可知Et是一个Q鞅。

由鞅表示定理可知：存在一个F Ft可料过程φt（称φt是F Ft可料过程，如果φt是F Ft可测的，其中使得：d Et＝φtd Dt。

设：ψt＝Et－φtDt。因此，如果在t时刻持有φt单位的基础资产和ψt单位的无风险资产（其价格为Bt＝ert），则t时刻组合的价格为：

并且，d Vt＝φtd St＋ψtd Bt，所以该策略是自融资的，其资产组合在t时刻的价格等于衍生品t时刻的价格，即：

由式（11）可以较容易地得到式（8）。事实上，对欧式看涨期权式（11）可写为：ct＝e－r（T－t）EQ［max（ST－K，0）］。不失一般性，求解c0。因ST在Q下服从对数正态分布，因此在Q下服从对数正态分布

设事件A＝｛ST＞K｝，则

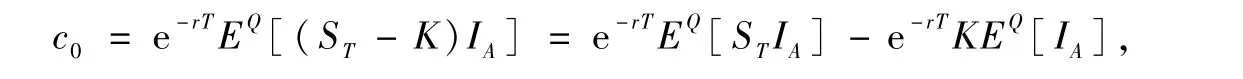
其中，IA为A的示性函数。在已知ST分布的情况下计算表达式中的两个期望是不难的。证毕。

可以看出，鞅方法将前面求解Black-Scholes微分方程的复杂过程变为简单的求随机变量的数学期望，这正是鞅方法的优势所在。

3 “希腊字母”及其意义

随着金融的高速发展，期权的定价理论得到了很好的发展，期权理论已趋向成熟，期权在实务中的应用也日趋频繁。虽然期权是一个很好的避险工具，但是期权的应用本身也会引发一定的风险，那么一个现实的问题就是：怎样降低由于期权的应用而引发的风险。希腊字母是衍生品的常用避险参数的总称［8－10］。这些避险参数度量了衍生品价格对各变量的敏感性，也引起了学者的关注［10－15］。本文结合欧式期权的定价公式，利用偏微分方程的方法重点介绍3种避险参数的表达式及意义。

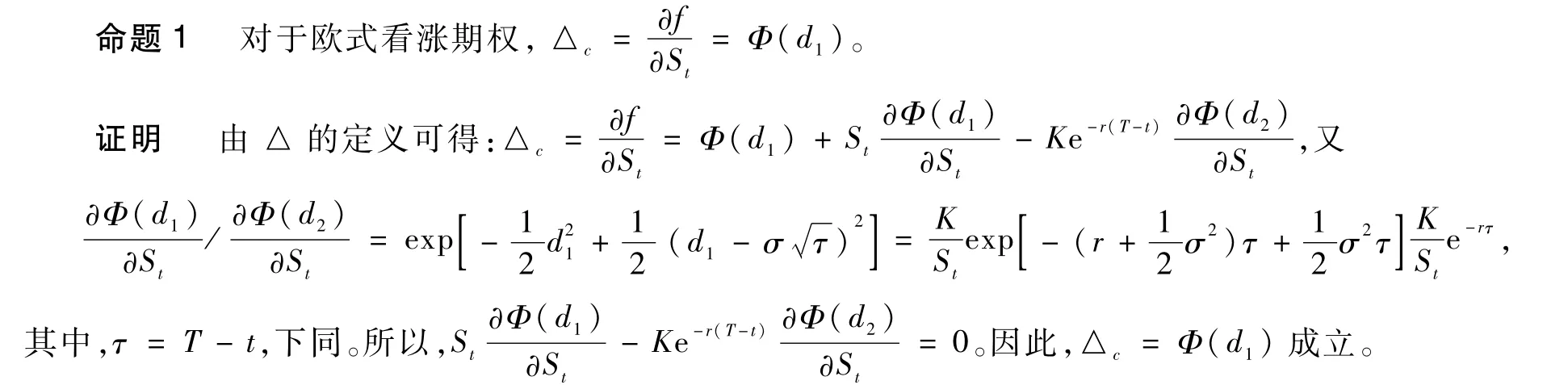
在实务中，△度量了基础资产价格波动对衍生品价格的影响，因此△是对资产价格敏感性的度量。由于每个资产都有△（基础资产本身的△＝1），因此通过调整资产组合中各个资产的权重，可能达到各单一资产按投资比例加权的△值为0，此时称资产组合处于△中立状态。这意味着基础资产价格的变动导致资产组合价格的该变量为0。△中立状态是风险管理者消除基础资产价格风险的最佳状态。

Γ度量了基础资产价格的变化对△的影响，即度量了衍生品价格与基础资产价格之间的凹凸性。如果某个时刻投资者处于△中立状态，当基础资产价格变化时，资产组合新的加权△的值可能不为0。Γ给出了如何重新回到△中立状态的方法。事实上，如果Γ＜0，则基础资产价格的上升将使得资产组合的△＜0，因此需要增加组合中有正△值资产的头寸以重新达到组合的△＝0。

v度量了基础资产价格波动性的变化对衍生品价格的影响。资产组合的v较小意味着资产组合的价格对基础资产价格波动率的变化不敏感。因此，对v较小的资产组合而言，没有必要花费较大的成本获得σs的准确值；反之，若组合的v较大，有必要获得σs较准确的信息。波动率σs不能直接观察到，通常情况下，σs是基于基础资产价格的历史数据估计出来的，这样得到的σs称为历史的波动率。另一种获得σs的方法是基于某个定价公式，如Black-Scholes期权定价公式，将被定价的价格用其市场价格代替，反解出σs，这样得到的σs称为隐含的波动率。两种方法哪种更好视具体情况而定。

［1］ Black F，Scholes M.The Pricing of Options and Corporate Liabilities［J］.JPol Econ，1973，81：637－659.

［2］ 胡支军.标的资产服从一般Itô随机过程的期权定价模型［J］.贵州大学学报：自然科学版，2003，20（1）：20－23.

［3］ 夏茜.伊藤过程的随机序及其应用［D］.武汉：华中科技大学，2011.

［4］ Stein-Erik F，Snorre L.Optimal Hedging Strategies for Multi-Period Guarantees in the Presence of Transaction Costs：A Stochastic Programm ing Approach［J］.European Journal of Operational Research，2008，185（3）：1680－1689.

［5］ Nele V，M ichèle V.A Locally Risk-M inimizing Hedging Strategy for Unit-Linked Life Insurance Contracts in a Lévy Process Financial Market［J］.Mathematics and Economics，2008，42（3）：1128－1137.

［6］ 闫海峰，陈春生.随机积分的Girsanov定理及其在期权定价中的应用［J］.河南师范大学学报：自然科学版，2003，30（1）：123，128.

［7］ 魏艳华，李艳颍，王丙参.条件期望的性质及求法［J］.牡丹江大学学报，2009，18（9）：116－117.

［8］ Domenico D G.Delta Hedging Strategies Comparison［J］.European Journal of Operational Research，2008，185（3）：1615－1631.

［9］ John C H.Options，Futures and Other Derivative［M］.Beijing：Huaxia Press，2000.

［10］ M iklavz M.Discrete-time Delta Hedging and the Black-Scholes Model with Transaction Costs［J］.Math Meth Oper Res，2006，64：227－236.

［11］ 武文娜，周圣武，黎伟.分数布朗运动下支付红利的亚式期权定价［J］.河南科技大学学报：自然科学版，2012，33（4）：100－104.

［12］ 陈兰兰.衍生品交易平台交易机制研究［J］.北方工业大学学报，2013，25（2）：14－20.

［13］ 毛月华.国际金融衍生品交易制度分析［J］.现代商业，2013（15）：40－41.

［14］ 冷菲.完善企业金融衍生品管理的设想［J］.冶金经济与管理，2013（3）：47－48.

［15］ 李培峦，张增援.离散化衍生品的定价［J］.河南科技大学学报：自然科学版，2013，34（6）：79－82.

O175

A

1672－6871（2014）05－0082－05

国家自然科学基金项目（11001274，11101126，11261010）；中国博士后基金项目（20110491249）；河南省教育厅科技重点研究项目（12B110006）；河南科技大学青年基金项目（2012QN010）；河南科技大学自然科学领域创新能力培育基金项目（2013ZCX020）

李培峦（1979－），男，河南鹤壁人，副教授，博士后，主要从事应用数学方面的研究.

2013－10－14