垂直交点APIT定位改进算法

杨凌云， 冯友宏

（安徽师范大学物理与电子信息学院，安徽芜湖 241000）

垂直交点APIT定位改进算法

杨凌云， 冯友宏

（安徽师范大学物理与电子信息学院，安徽芜湖 241000）

针对APIT算法存在的问题，提出了一种新的判断未知节点位置的方法。首先选择3个任意组合的锚节点，通过任意一个锚节点对另外两个锚节点所在直线作垂线得到垂直交点，通过比较这个锚节点到交点的距离和它与未知节点的距离的关系，初步判断未知节点位置，同时，通过加权质心定位算法得到未知节点的精确估计值。Matlab仿真结果表明，改进后的算法相比较经典APIT算法在定位精度上有了很大提高。

APIT；垂直；交点；加权；质心算法

0 引 言

无线传感器网络是一种基于低成本、低损耗的自组织无线定位网络，能够实现恶劣环境下的信息采集和跟踪工作［1］。在无线传感器网络中，网络内传感器节点的自身定位是一项非常关键的技术，定位精确的高低直接影响着整个网络在以后工作中的定位跟踪能力。节点自身定位方法一

般分为基于距离的定位算法和距离无关的定位算法两大类［2］，后者因为不需要知道自己与锚节点的角度、距离等信息，而通过信息连通度等信息估计出节点位置信息，这种定位方法因为需要传递的信息少，能很好地节约节点能力，实现较长的工作时间而得到广泛应用和研究，比较常见的与距离无关的定位算法有：dv-hop、质心定位［3］、APIT定位［4］等。其中质心定位算法是一个粗定位算法［5］，APIT算法在节点连通度比较大的情况下定位精度较高［6］，后来就有人把质心定位与APIT结合［7］，提出了基于APIT的质心定位算法。文中针对这种算法的APIT算法在定位过程中的一些问题，在基于APIT的质心定位算法的基础上提出了改进措施，提高了APIT的定位精度。

1 APIT算法

1.1 PIT测试

在能够通信的范围内，找出所有能够与未知节点通信的锚节点，任意选取其中的3个节点，判断未知节点是否在这3个节点组成的三角形内部，如果再进行下一步定位运算，如果不在三角形内部，则丢弃这个三角形。判断是否在三角形内部的方法如果未知节点朝某个方向发生移动，是否是同时远离或者同时接近这3个锚节点，如果是，则未知节点在三角形外面，如果同时有接近和远离的节点，则在三角形里面［8］。

在实际应用中，节点的移动是非常缓慢的，或者说在一定条件下可以近似地认为我们的很多无线传感器网络是一个静态网络，节点是静止的。针对静态无线传感器网络，文献［4］提出可以根据未知节点的邻居节点是否同时远离和接近三角形节点来判断未知节点是否在三角形内部的近似PIT算法（简称in-out算法）。

静态无线传感器网络中的近似PIT测试是APIT算法的核心，判断的正确与否直接关系着未知节点定位的精确度。但是在这种算法中，未知节点的邻居节点的分布是一个随机分布，它们之间的距离可大可小，方向可左可右，特别是靠近三角形某一边时，对选取不同的邻居节点，得到的结论可能就会不同，从而造成较大误差。为此，文中根据三角形中垂线的一些特征，可以粗略估计未知节点位置信息［9］，提出一种新的未知节点判断方法，可以相对准确地判断出未知节点的位置。

1.2 定位算法

如果找到由3个以上锚节点组成的三角形的未知节点，就可以对未知节点进行定位，假设一般情况下未知节点仅可以接收到已知锚节点的位置和发出时的能量值和接收到的能量，那么根据通用的能量传递公式［10］，能量的传递与距离的平方是成反比例的关系，即

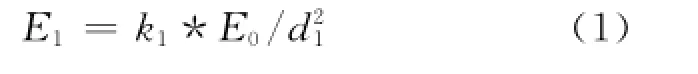
式中：E1——到达未知节点的能量；

E0——锚节点发送时刻的能量；

d1——未知节点与锚节点的距离；

k1——常数，它与信号波长、传输环境等信息有关，特定的条件下为一常数。

通过能量比值可以得到相对精确的距离值。在求锚节点包围的未知节点的位置信息时，常见到的就是网格扫描算法和质心定位算法。在网格扫描算法中，网格的精度直接关系着定位精度，所以很容易出现位置估计不足的问题［11］。在质心定位算法的基础上加入相应权值，可以得到较为精确的估计值［12］，文中提出加权质心定位算法，加入与能量有关的加权因子，可以得到更为精确的位置估计值。

2 算法改进

这里提出一种新的基于APIT的改进算法

NP-APIT算法，首先根据三角形垂直分割线的特征［13－14］，提出一种新的in-out判别方法，然后对质心定位算法加入与能量有关的权值估计，提出APIT算法的估计精度。

2.1 in-out算法改进

定理1 如果一个点位于三角形的内部，那么该点与任意三角形的上点位于另外两个点位于的直线的划分的平面的一侧，如图1所示。

图1 D点在三角形内部

图中，如果D点位于三角形ABC内部，BC所在直线把平面划分两部分，那么A点和D点一定在直线的同一边，同样可以证明，B点与D点的关系、C点与D点的关系也成立。

证明 图1中，D点为未知节点，A点、B点和C点为已知锚节点，假设在D点能接收到3个锚节点分别发送过来的各自坐标信息和能量信息，那么由式（1）可得，通过接收到的能量值与锚节点发送时的能量进行比值，可以得到两者之间的距离，即可以得到未知节点分别到3个锚节点距离为：

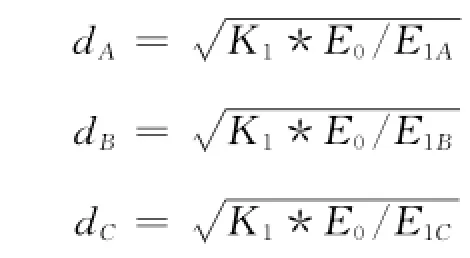
过未知节点D作BC的垂直平分线，与BC的交点为E，根据数学直线计算公式很容易求出E点坐标与锚节点B和C之间的位置关系，得到E点坐标。如果A点与D点在同一平面内，那么D点到A点的距离dA一定小于AE的值，如果dA大于AE的值，则A点和D点在不同的平面上。同样的方法可以判断B点、C点与D点的关系，从而得出D点是在ABC所组成的三角形内部，那么它到某一个锚节点的距离一定小于它到另外两个锚节点所在直线的垂直交点的距离。

定理2 如果一个点位于三角形的外部，那么至少有一个三角形的顶点与未知节点分别位于另外两点所在直线划分的平面。

D点在三角形外部如图2所示。

图2 D点在三角形外部

证明 图中，A点和D点分别位于BC所在直线划分的两个平面上，B点也和D点在AC所在直线划分的两个平面上，而C点与D点在AB划分的同一平面内。我们只需要证明只要有一个点与D点不同面就可以证明D点在ABC组成的三角形外。

对于图2中未知节点位于三角形外面的情况，如果说D点位于离三角形比较近的地方（由D点所作三角形一个边的垂直平分线正好位于三角形的两顶点之间，图1中E的位置），那么上述方法很容易判断，但是如果所作垂线的交点在连线的外部，那么根据接收到的信息就有可能判断不出来或者出现判断错误的情况。我们的方法是，先假设未知节点是在三角形内部的，这样利用直线公式，很容易计算出F的位置，F点与真正的垂直交点E是三角形的顶点C的对称（CF＝CE），如果AF＜AD的值，D点在三角形外，反之在三角形内。同样的方法可以另外两边。

具体说明如下：

1）图2给出了三角形中两个点与D点不在一个平面的情况，它具有一定代表性。通过不断实验发现，在判断中可能出现3个锚节点中的一个锚节点、两个锚节点甚至3个锚节点与未知节点不在直线所划分的同一平面内，可以推导得出同样的结论。

2）在位置判断过程中，如果未知节点在离三角形外不远处的位置，有可能出现三角形的某一个节点的误判，但只会出现本来在两个节点在不同平面内，结果误判的情况，但这不会影响整个判断结论，另外两个节点肯定会判断出来的，图2中的情况就是一个有可能出现一边误判，但不会影响最终结果的情况。

3）对于未知节点可能在三角形某一个边所在直线的情况，未知节点在三角形外部时，我们取的交点其实是一个对折过去的虚交点，可以很好地区分未知节点在两个锚节点中间某个位置还是外侧。定理2同样适用。

2.2 加权质心定位

对于已知未知节点位于由已知锚节点组成的三角形内部的节点，采用质心加权的方法来估计未知节点的未知，同时，把未知节点一定在3个垂直交点所组成的三角形内作为约束条件，来进一步精确未知节点。

加权垂直平分节点组成的约束区间如图3所示。

图3 加权垂直平分节点组成的约束区间

在图1中，分析了锚节点三角形内部未知节点与其中一个边的位置关系，找到了其中的过未知节点的垂直平分交点，同样的方法可以找到另外两边的垂直平分交点，把这三点连接起来构成新的三角形，而未知节点D一定在这个新三角形内部阴影部分（见图3），这就缩小了选择的范围。在对锚节点进行加权质心加权的同时，满足约束条件的点才符合我们要求的估计值。

同时对三角形质心加权定位估计值为：

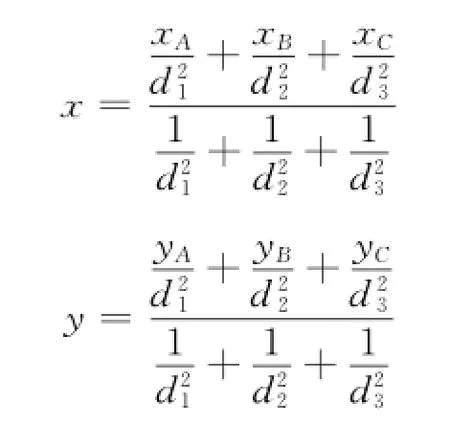
这里设三角形的3个点分别是A点坐标（xA，yA）、B点坐标（xB，yB）和C点坐标（xC，yC），未知节点到这3个锚节点的距离分别为dA，dB，dC。因为距离的平方与初始能力和接收能量成正比例关系，所以权值实际上是E0／Ei，E0为初始能量值，Ei为接收到的能量值。实验证明，对能量进行加权（即对距离的平方进行加权）比简单的对距离进行加权可以得到更高的准确度。

3 算法仿真

采用Matlab对上面两种算法进行仿真分析，并在40m×40m的环境中进行测试，对不同锚节点、不同的通信半径下，通过两种不同的算法对未知节点进行位置估计的误差进行比较，如图4所示。

图4 定位误差随着通信距离的变化图

图4中的通信半径的变化范围为10～30m。可以看到，改进的基于垂直交点算法几乎在每个不同的通信范围下，都可以得到更低的而且相对稳定的定位误差，误差减少为APIT误差的20%左右，同时，因为测试的区域范围是40m的一个正方形，可以看到在锚节点通信距离大于20m后变化趋于平稳，所以，并不是锚节点的通信距离越大越好，合适的通信距离既可以节约成本，也可以得到很好的定位效果。

定位误差随着锚节点个数的变化如图5所示。

图5 定位误差随着锚节点个数的变化图

图5中锚节点的个数是从20个开始仿真的，每次增加5个锚节点，通过仿真可以看到，改进后的NP-APIT算法的误差几乎下降到APIT算法的40%左右，而且误差值相对稳定。综上所述，改进的NP-APIT算法的误差将比APIT算法减少了定位误差，有效提高了定位精度。

4 结 语

在静止无线传感器网络中，针对APIT算法中的in-out判断方法和质心定位算法进行了改进，提出了通过对加权垂直分割节点到锚节点距离和未知节点到锚节点距离的比较，来判断一个锚节点和未知节点是否同在两个锚节点形成的直线所划分的同一个平面内来进行未知节点的inout判断，同时在位置估计中，采用了加权质心定位和未知节点一定在垂直分割点形成的三角形中的约束条件，有效提高了定位精度。

［1］孙利民，李建中，陈渝，等.无线传感器网络［M］.北京：清华大学出版社，2005：151-152.

［2］Niculescu D，Nath B.DV based positioning in ad hoc networks［J］.Journal of Tele-communication Systems，2003，22（4）：267-280.

［3］Bulusu N，Heidemann J，Estrin D.GPS-less low cost outdoor localization for very small devices［J］.IEEE Personal Communications Magazine，2000，7（5）：28-34.

［4］He Tian，Huang Chengdu，Blum B M，et al.Range-free localization schemes in large scale sensor networks［C］／／Proceedings of the 9th Annual International Conference on Mobile Computing and Networking，USA：MOBICOM′2003，San Diego，CA，2003：81-95.

［5］Rout C S，Krishna S H，Vivekchand S R C.Hydrogen and ethanol sensors based on ZnO nano wires and nanotubes［J］.Chemical Physics Letter，2006， 418：586-590.

［6］徐小玲，张福强，李少彪.基于APIT的无线传感器网络质心算法研究［J］.传感器与微系统，2011，7（30）：57-63.

［7］陈维克，李文锋，首珩，等.基于RSSI的无线传感器网络加权质心定位算法［J］.武汉理工大学学报，2006，30（2）：265-268.

［8］冯秀芳，崔秀锋，祈会波，等.无线传感网络中基于移动锚节点的APIT的改进定位算法［J］.传感技术学报，2011，24（2）：269-274.

［9］杨骥，刘锋.无线传感器网络基于中垂线分割的APIT的改进定位算法［J］.传感技术学报，2008，21（8）：1453-1457.

［10］Li D，Hu Y H.Energy based collaborat ive source localizat ion using acoust ic micro-sensor array［J］.Journal EUROS IP Applied Signal Processing，2003（4）：321-337.

［11］姚艳，禹继国，郭强.基于网格扫描的无线传感器网络定位算法［J］.计算机工程，2012，38（9）：86-89.

［12］周彦，文宝，李建勋.无线传感器网络节点近点加权质心定位方法［J］.计算机工程与应用，2012，48（1）：87-89.

［13］万国峰，钟俊.基于三角形理论的无线传感器网络定位算法［J］.计算机应用研究，2013，1（7）：249-251.

［14］杨凌云，冯友宏.一种新的无线传感器网络半动态分簇路由协议［J］.长春工业大学学报：自然科学版，2010，30（1）：48-51.

A modified APIT localization algorithm based on perpendicular intersection features

YANG Ling－yun， FENG You-hong

（The College of Physics and Electronic Information，Anhui Normal University，Wuhu 241000，China）

To overcome the flaws in APIT algorithm，a new method to identify the unknown nodes is put forward.First，three random anchor nodes are chosen，and then the perpendicular intersection is obtained，where the vertical through any one node goes to the line of other two nodes.By comparing the distance of the node to the intersection with the one to the unknown node，the location of the unknown node can be determined.The position of the node can be calculated with the centroid algorithm.Matlab simulation results show that the modified APIT algorithm is with higher precision than that of classic one.

APIT；perpendicular；intersection；weighting；centroid algorithm.

TP 393

A

1674-1374（2014）01-0096-05

2013-11-21

安徽省高校自然科学基金（KJ2010B350）；国家“863”电动汽车重大专项基金（2011AA11216A）

杨凌云（1983－），女，汉族，河南周口人，安徽师范大学讲师，主要从事无线网络方向研究，E-mail：lingyun716＠126.com.＊通讯作者：冯友宏（1979－），男，汉族，安徽池州人，安徽师范大学副教授，主要从事无线网络方向研究，E-mail：yhfeng0215＠126.com.