固定频率分配问题的综述*

佈仁巴图

(内蒙古大学数学科学学院，内蒙古呼和浩特010021)

固定频率分配问题的综述*

佈仁巴图

(内蒙古大学数学科学学院，内蒙古呼和浩特010021)

本文对固定频率分配问题进行了简单的介绍，叙述了固定频率分配问题中所考虑的干扰因素、数学模型，并且讨论了固定频率分配问题的一些典型的算法。

固定频率分配;干扰因素;算法

1 引言

无限电频率是一种有限的资源，随着移动通信网络的飞速发展，移动通信设备已经成为了人们在日常生活中不可缺少的通讯工具。根据联合国有关机构调查，在2014年初，手机用户超过70亿，目前世界71亿人口中68亿手机用户。根据工业与信息化部网站数据显示，随着服务能力持续提升，截至2014年中国大陆手机用户已经超过了14.77亿。高速增长的用户数量，即频率使用需求量与有限的频率资源之间的矛盾越来越激烈。如何将有限的频率资源合理的分配面临着一个新的挑战。所以研究频率分配问题是一个非常有意义的工作。

频率分配问题是一种典型的NP－Complete组合优化问题，而固定频率分配问题是最典型的、最常用的一类频率分配问题。过去常用的频率分配算法有:启发式算法、图形着色算法等等。这些算法求解频率分配问题时，花费时间较长，效果也不太理想。近年来，随着利用计算机模仿人类电脑、生命进化过程、生物群体行为、物理现象的智能技术和智能算法的发展，出现一些智能优化算法来解决频率分配问题。如遗传算法、禁忌搜索算法、模拟退火算法、蚁群算法、粒子群优化算等等。

2 频率分配问题的相关知识

2.1 固定频率分配问题的简介

这是典型的一种频率分配方式。是在固定的频率集合下，将服务区域被分成多个蜂窝小区，根据每个小区的频率使用数据需求和电磁干扰约束对各个小区进行分配频率，使求得总干扰数最小化的分配方案。

2.2 频率复用

频率复用的原理是源于无线电波传播路径损耗特性的，即如果两个小区之间距离足够大，那么用于一个小区的频率可以在另一个小区上同时复用，这样可以提高频率的利用率。

2.3 电磁干扰约束

由于电磁波在传播过程中，遇到相同或相近的电磁波时，出现一些电磁干扰。在频率分配问题中主要考虑的干扰有:同频干扰、邻频干扰、同址干扰、互调干扰。

(1)同频干扰约束(Co－Channel－Constraints.简称CCC)

在分配频率时，在距离较近的两个或多个小区内同时不能分配相同的频率，必须在干扰范围以外的小区内可以同时分配同样的频率。

(2)邻频干扰约束(Adjacent－Channel－Constraints.简称ACC)

在给两个邻近小区分配频率时，必须满足所要分配的频率间隔大于或等于某一个预先知道的特定值。也就是说间隔较小的两个或多个频率不能分配给较近的小区。

(3)同址干扰约束(Co－site－Channel－Constraints.简称CSC)

对于给某一个小区内分配频率时，也需要满足所分配的频率间隔大于或等于某一个预先知道的特点值。也就是说间隔较小的两个或多个频率不能分配给同一个小区。

(4)三阶互调干扰约束(Third－Order－Interception－Constraints.简称TOIC)，互调干扰是指分配某一个小区的频率fi和频率fj经过非线性作用后出现的新频率fk，接近或相同本小区或者相邻小区的频率时产生的干扰。可以分为二阶互调干扰、三阶互调干扰等等。其中三阶互调干扰是最严重的互调干扰。

由频率fi和频率fj产生的二阶、三阶、四阶互调干扰下产生的新频率(或产生物)可以定义如下:

(ⅰ)由频率fi和频率fj产生的二阶互调产生物:fi±fj;

(ⅱ)由频率fi和频率fj产生的三阶互调产生物:fi± 2fj，2fi±fj，fj－2fi，2fj－fi;

(ⅲ)由频率fi和频率fj产生的四阶互调产生物:2fi± 2fj，3fi±fj，3fj±fi，fi－3fj，fj－3fi。

3 固定频率分配问题的数学模型

1982年A.Gamst和W.Rave提出了频率分配问题的经典数学模型，在该模型中构造了一个兼容矩阵C，假设小区的个数为N，则这个兼容矩阵就是一个N×N维的对称矩阵，即形式为:

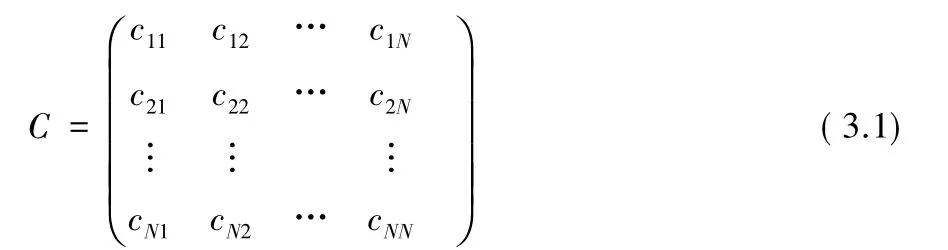
其中矩阵C的元素cij表示分配给小区i和小区j的频率最小频率间隔，cij=0表示小区i和小区j可以复用频率，对角元素cij(i=j)表示小区i(或小区j)的同址干扰约束，即小区i(或小区j)中频率之间所需要的最小间隔。除了兼容矩阵之外还需要构建各小区所需要的频率个数向量D，即形式为:

其中需求向量D的元素di，表示第i小区的频率需求个数。

数学模型1:

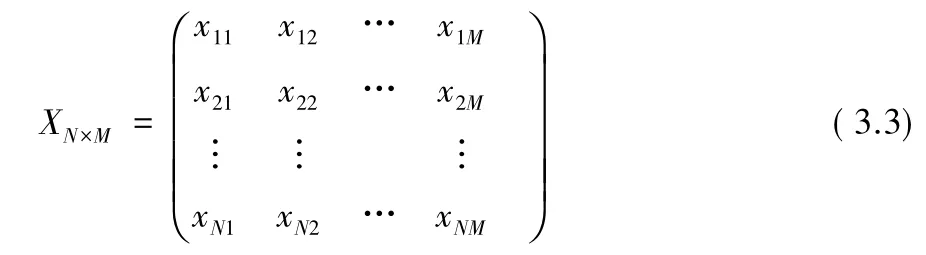
其中

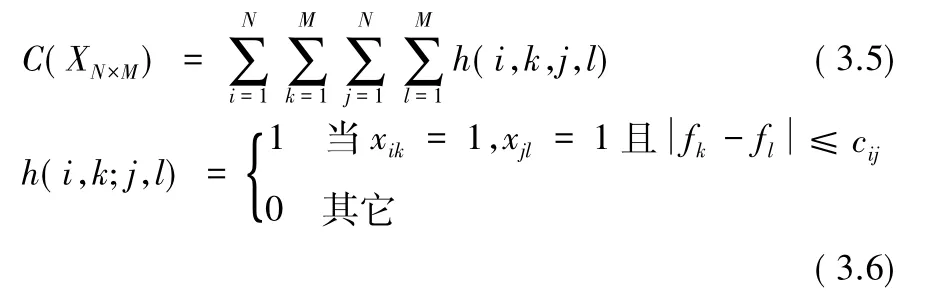
则，固定频率分配策略的数学模型为:

s．t

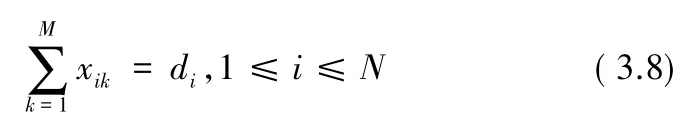
数学模型2:

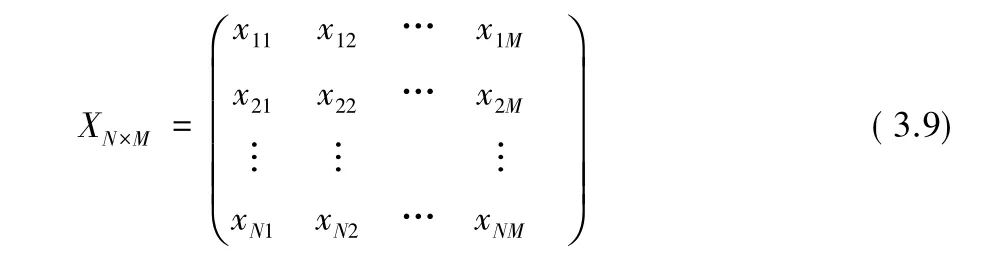
其中

小区i的需求约束可以描述为:

小区i的同址干扰(CSC)约束可以描述为

小区i与小区j的同频干扰(CCC)、邻频干扰(ACC)约束可以描述为:

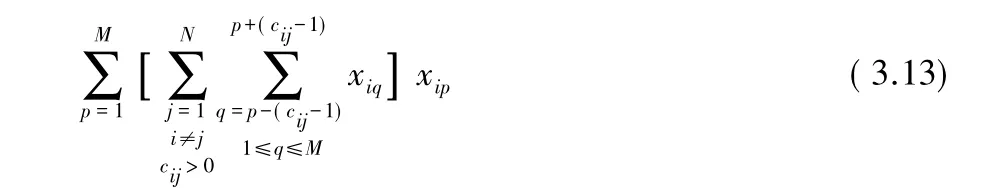
则，电磁兼容约束函数为:

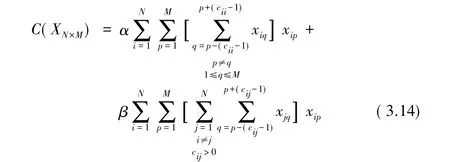
(其中α+β=1)则，固定频率分配策略的数学模型为:

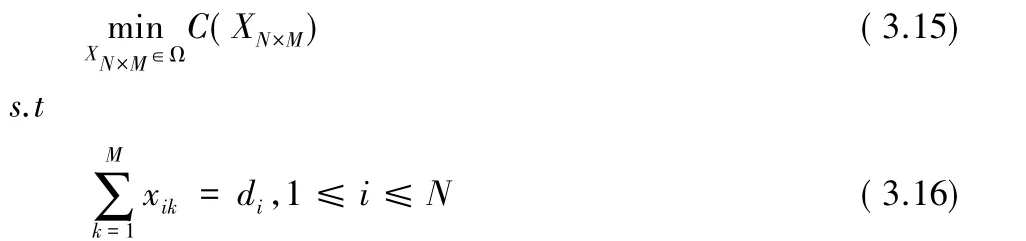
4 固定频率分配问题的算法研究

4.1 启发式算法(Heuristic－Algorithm.简称HA)

4.1.1 频率穷举搜索算法(Frequency－Exhaust－Algorithm.简称FEA)

从小区列表的顶部开始，将当前频率分配给当前小区，如果频率不与已分配好的频率发生冲突，则将该频率分配给当前小区，否则试探下一个频率是否合适，直到所有频率全部试探完毕。

4.1.2 需求穷举搜索算法(Requirement－Exhaust－Algorithm.简称REA)

将从第一个频率开始，将当前频率按小区列表的顺序逐一进行试探性地分配，如果当前频率能够对已经分配好的频率不产生干扰，则将该频率分配给当前小区。否则继续试探下一个小区是否适合，直至所有小区试探完毕。

4.1.3 后向回溯算法(After－the－Backtracking－Algorithm.简称ATBA)

后向回溯是最简单的穷举搜索算法，小区被顺序分配频率.首先从频率集合D中取出频率fk分配给小区i，即fik=1 .然后检查已经分配频率的小区j，j＜i是否有违反约束的情况发生.如果没有违反，则接着进行下一个小区的频率分配，这一步骤称为前向移动。如果有违反，则从频率集合中取出下一个频率分配给小区i，即fik+1=1，如果频率集合D中所有的频率都不能满足所有约束，则回溯一步，对前一个小区i－1重新进行频率分配。

4.1.4 前向检测算法(Former－to－the－Backtracking－Algorithm.简称FTTBA)

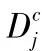
4.2 智能算法(Intelligent－Algorithm.简称IA)

4.2.1 遗传算法(Genetic－Algorithm.简称GA)

遗传算法是20世纪70年代由美国密执安(Michigan)大学约翰·霍兰德(John.Holland)教授提出的一种模拟生物在自然环境中的遗传和进化过程而形成的自适应的全局优化概率搜索算法，

遗传算法求解固定频率分配问题时，首先对实际的频率分配问题进行编码，解决频率分配问题时常用的编码方式有:二进编码、最小间隔编码、实数编码。

让后产生初始种群进行交叉、变异操作，最后对个别个体进行局部寻优。

4.2.2 蚁群算法(Ant－Colony－Algorithm.简称ACA)

蚁群算法是由意大利学者马克·多里戈(Marco Dorigo)在1991年提出的模仿群体在寻找食物或寻找回巢的路径时，根据它们前面蚂蚁留下的化学物质，称之为“信息激素(Pheromone)”作为信息，寻找信息素浓度较大的路径的群体行为的一种优化算法。

蚁群算法求解固定频率分配问题时，首先需要构造有N个顶点，每对顶点之间有M条边的多边图G。假设系统有q只蚂蚁，则每一只蚂蚁走过多边图G的路径代表一种频率分配方案。

4.2.3 粒子群算法(Particle－Swarm－Algorithm.简称PSA)

粒子群算法是1995年由美国心理学家肯尼迪(James Kennedy)和电气工程师埃伯哈特(Russell Eberhart)提出的一种模仿鸟群寻觅食物行为的智能算法。

粒子群算法求解固定频率分配问题时，首先将每一种频率分配方案类比于搜索空间的一个无质量、无体积、有速度的粒子。然后随机的选择初始种群，进行迭代，在每次迭代中每一个粒子往历史局部最优解Pbest方向飞行。

4.2.4 模拟退火算法(Simulated－Annealing－Algorithm.简称SAA)

模拟退火算法是由米特罗波利斯(Metropolis)在1953提出的一种优化算法，在1983年柯克帕特里克(Kirkpatrick)将模拟退火算法成功地应用在组合优化问题领域。

5 总结和展望

本文从固定频率分配策略中主要考虑的电磁干扰约束、数学模型、典型的算法等几个方面对固定频率分配问题进行了总结。固定频率分配问题是频率分配问题的一类典型的、过去常用的频率分配策略。由于在实际通信网络中，每个小区的频率使用需求是随着时间、空间等因素发生变化的。然而固定频率分配策略中所讨论的小区频率需求是固定的。为了克服固定频率分配策略对频率使用需求的时间和空间变化缺乏自适应性的缺，出现了点动态频率分配策略、混合频率分配策略等新的频率分配策略。目前频率分配问题的大部分算法都集中在固定频率分配问题的研究，研究动态频率分配、混合频率分配策略的算法很少。

［1］孙媛媛.基于遗传算法的GSM网络频率规划优化研究与应用［D］.北京邮电大学，2008.

［2］W Gamst，Rave.On Frequency Assignment in Mobile Automatic Telephone Systems［J］.In.Proc.GIOBLECOM，1982，82:309－315.

［3］赵秋红，肖依永.基于单点搜索的元启发式算法［M］.北京:科学出版社，2013.

［4］古邦伦.电磁频谱管理中的频率分配技术研究［D］.国防科学技术大学，2006.

［5］郭文志，陈国龙.离散粒子群优化算法及其应用［M］.北京:清华大学出版社，2012.

［7］韦景俐.离无线电网络规划中的频率规划研究［D］.北京邮电大学，2012.

［8］范晓光.频率分配算法适用性研究.［D］解放军信息工程大学，2010:2－37.

［9］高亚男.有效的优化算法在频率分配上的应用［D］.新疆大学，2010:21－43.

［10］石飞.GSM无线网络优化中的有效的频率分配方法的研究［D］.新疆大学，2012:21－43.

［11］何迪.基于选择性变异技术的频率分配方法［D］.新疆大学，2011:1－39，55－67.

［12］玄光男，程润伟.遗传算法与工程优化［M］.北京:清华大学出版社，1999.

Fixed Frequency Assignment Problem

Burenbatu
(School of Mathematical Sciences，Inner Mongolia University;Hohhot 010021)

In this paper，the fixed frequency assignment problem has carried on the simple introduction，describes the interference factors of fixed frequency assignment problem，mathematical model，and discusses the fixed frequency assignment problem of some typical algorithms.

fixed frequency assignment problem;interference constraints;algorithm

TN925

A

1004－1869(2014)02－0033－04

2014－04－12

佈仁巴图(1987－)，男，蒙族，内蒙古锡林郭勒人，2011级硕士研究生。