四直升机协调吊挂系统模型跟踪非线性控制

宋彦国，王焕瑾

(南京航空航天大学航空宇航学院，210016 南京)

四直升机协调吊挂系统模型跟踪非线性控制

宋彦国，王焕瑾

(南京航空航天大学航空宇航学院，210016 南京)

基于直升机控制输入逆解的方法，研究了多直升机吊挂系统的控制问题.多直升机协调吊挂系统在外载荷的影响下每一架直升机具有不同的稳定性和响应形式，根据直升机气动力模型和飞行动力学模型，提出基于直升机空气动力学逆的控制输入逆解非线性模型跟踪控制器设计方法.该控制方法的显著优势是能直接处理吊索力反馈，保证多直升机吊挂系统中每一架直升机具有相同的控制律并能有效抑制吊索力扰动，且使每一架直升机具有相同的稳定性和响应特点.仿真结果证明了四直升机的协调吊挂非线性控制方法的可行性和正确性.

多直升机;非线性控制;模型跟踪;飞行动力学;吊挂载荷

当前对重型直升机的需求变得越来越迫切，但是体积重量的增加导致重型直升机的复杂性成倍的增加，经济性显著减低［1－2］.对于重型载荷垂直运输的一种可替代的方案是使用多架直升机协调运送重型货物［3－4］.

早期多直升机的协调吊挂飞行动力学特性的研究局限于悬停/小速度飞行的定常状态［5］，采用线性化模型分析多直升机协调吊挂系统的增稳増控系统.文献［6］研究了多直升机协调吊挂系统的手动操纵模式，飞行员给出的飞行品质评价为不可接受.文献［7］提出了非线性方法对多直升机吊挂系统的降阶模型进行非线性控制，并对非线性控制器的性能进行了评估.文献［8］采用线性二次型高斯/回路传递复现(LQG/LTR)技术设计了多直升机吊挂系统的鲁棒稳定控制器.文献［9－12］采用基于反馈线性化的非线性控制器设计技术以增强多直升机协调吊挂系统的稳定性，同时简化飞行员的操纵负荷.文献［13－14］为飞行员提供辅助设施保证载荷运输的稳定控制.文献［15－16］采用前馈反馈相结合的自适应控制方案，实现吊挂载荷的稳定运输并减少吊挂载荷的摆动.文献［17］在控制系统中引入吊索的角度反馈来提高直升机的飞行品质.

多直升机吊挂载荷系统的吊索力可以直接测量，但是在控制器设计过程中缺少吊索力与舵机的传递关系，因此前述方法都没有在控制器中直接综合考虑可测量的吊索力，而可测量的吊索力是显著影响直升机飞行品质的重要因素，直接反馈对提高吊挂直升机的飞行品质至关重要，本文提出了吊索力直接反馈非线性逆控制方法.

1 四直升机协调吊挂系统非线性飞行动力学

为了进行多直升机协调吊挂系统控制与航电系统设计，建立了四架UH60直升机协调吊挂系统的非线性飞行动力学模型，建模中考虑了非线性直升机飞行动力学模型，非线性六自由度载荷动力学模型，他们通过弹性吊索紧耦合在一起，所有动力学模块顺序协同工作，图1为四直升机协调吊挂系统的配置形式示意图，图2～5为自然直升机和协调吊挂系统中每一架直升机随着飞行速度增加的特征根分布情况.

图1 四直升机吊挂系统示意图

图2 直升机1与无吊挂直升机根轨迹

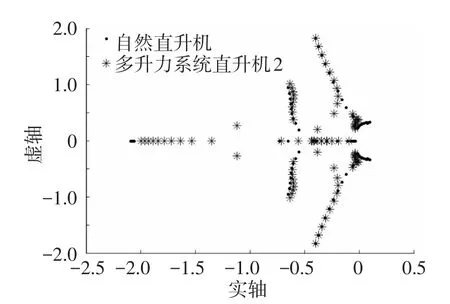
图3 直升机2与无吊挂直升机根轨迹

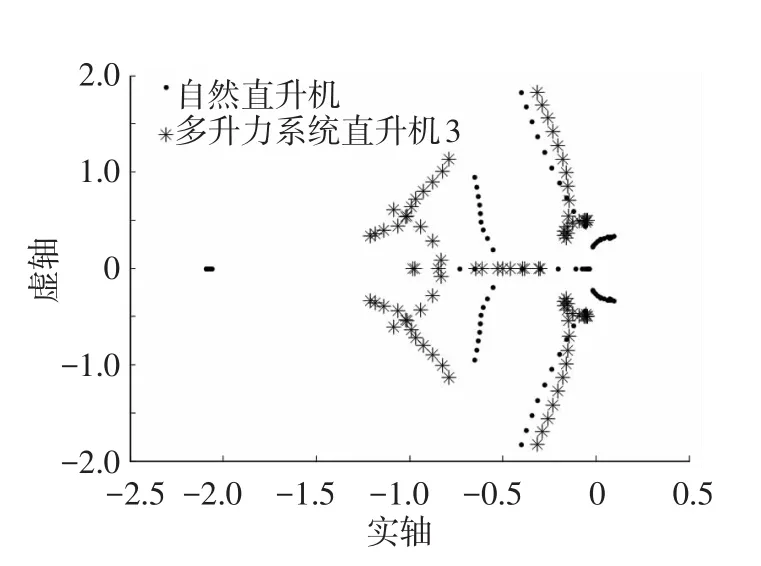
图4 直升机3与无吊挂直升机根轨迹

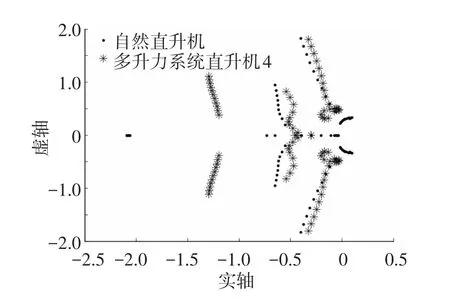
图5 直升机4与无吊挂直升机根轨迹

由图1～5可得如下结论:

1)系统中的直升机吊挂形式不同、位置不同、每一架直升机的稳定性不同;

2)每一架直升机的稳定性随着飞行速度的增加特征根变化明显;

3)每一架直升机的时域响应特点明显不同，这对多直升机的协调控制提出了挑战.

需要强调的是，特征根的分布与载荷重量、直升机分布、飞行状态密切相关，因此特征根的分布并非一成不变，这就要求控制系统的设计应具有很强的鲁棒性，同时应考虑:

1)控制器应当使每一架直升机具有相同的稳定性、时域响应，简化协同控制难度;

2)弹性吊索的外力影响了每一架直升机的特性，如果控制器中直接采用的吊索力反馈控制能很好的消除这种不确定性，同时控制器也具备了外挂载荷摆动抑制的能力.

2 控制输入逆解控制

2.1 控制策略

基于控制输入直接解方法的出发点类似于飞行员对直升机的控制过程，将直升机视为一个真实的物理对象，当飞行员期望控制直升机到达一个期望的状态时，他们根据当前的飞行状态给定控制输入，并能不断的修正控制输入，使直升机达到指定的期望状态.直升机飞行动力学模型可以写为

式中:X，Y，Z，L，M，N 为体轴系外力和外力矩;u，v，w，p，q，r，φ，θ，ψ 分别为体轴系速度，角速率和欧拉角;带有下标的M和I为直升机惯性系数.

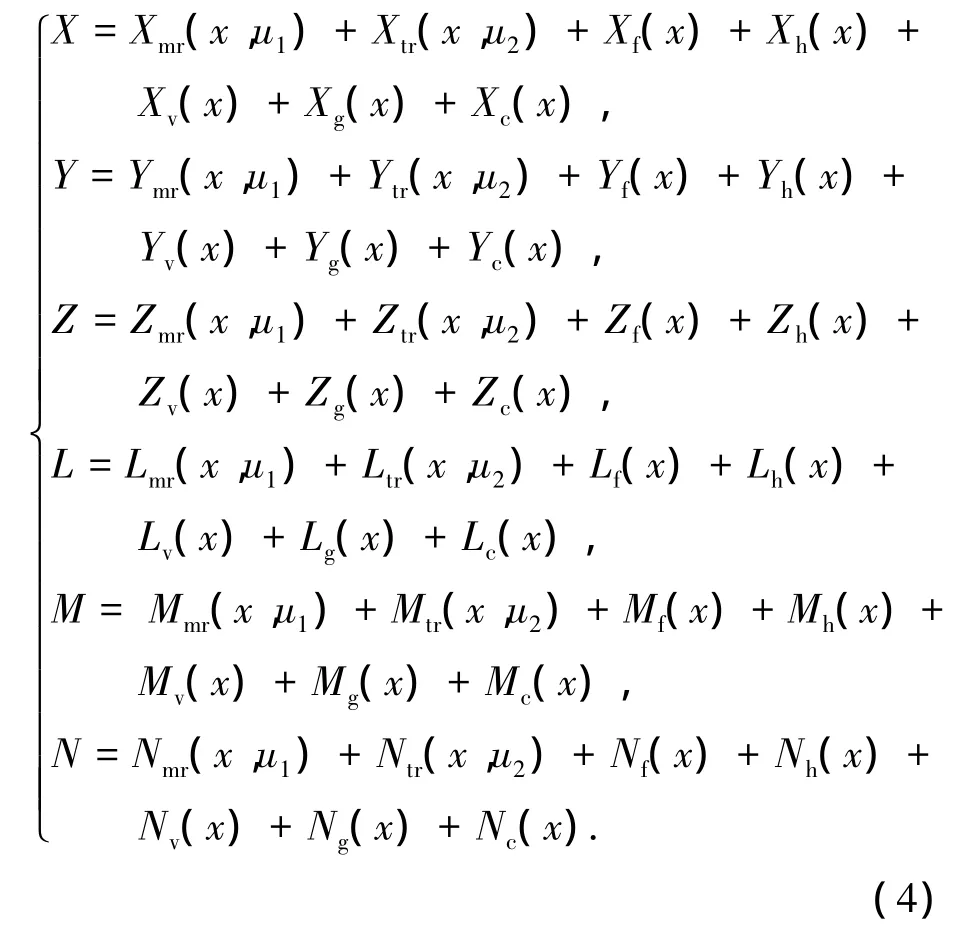
式中:x 为飞行状态;控制输入 u1=［θ1c，θ1s，θ0］分别为旋翼的纵横向周期变距和总距;u2=［θ0tr］为尾桨距;下标分别代表:mr为旋翼、tr为尾桨、f代表机身、h为水平尾翼、v为垂尾、g代表重力，c为弹性吊索.

方程(4)中除了主旋翼和尾桨外，其他空气动力学部件所产生的空气动力与飞行状态有关.因此只要基于直升机飞行状态反馈，就可以获得直升机机身、尾翼、起落架等部件在当前状态下的空气动力.式(4)中吊索力矢量可以通过直升机吊钩传感器直接测定.

如果期望指令为高度与欧拉角［Zr，φr，θr，ψr］，下标r表示期望，通过二阶指令滤波器可以获得，通过式(3)获得，如果将期望指令代入式(1)～(2)右侧，并且将与操纵量不相关的空气动力移到方程的右侧，可以得到如下的方程:

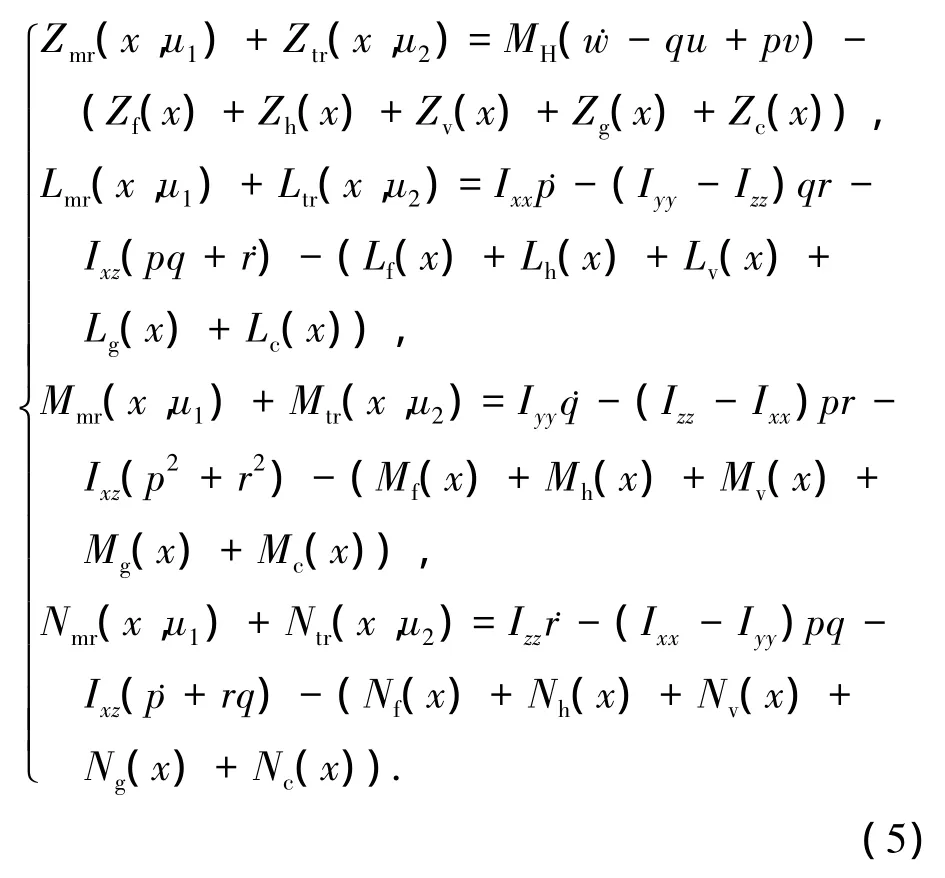
上述方程右侧已知，物理意义是:根据当前的飞行状态，要实现期望的飞行状态而需要的外力矢量，由旋翼和尾桨产生;如果能根据外力矢量求出直升机的操纵量的大小，即可实现期望的直升机飞行状态.将已知操纵量和当前飞行状态求取旋翼和尾桨的空气动力视为正向过程，那么可以将已知期望旋翼尾桨产生的空气动力和当前的飞行状态求取操纵量大小视为控制输入逆解.

将方程(5)代入方程(1)～(2)，可以得到下式:

容易验证下式是上式的解:

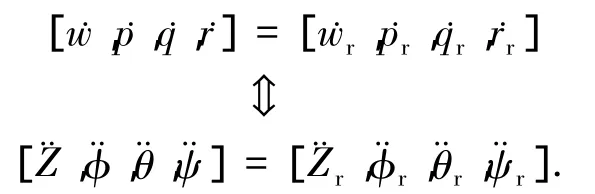
上式将直升机这一复杂非线性飞行控制问题转化为一个线性系统.下一步是如何根据期望状态和当前飞行状态进行旋翼尾桨控制输入求解，建立非线性逆模型.

2.2 控制输入逆解

本文所采用的空气动力学模型详见文献［18］.首先，分析主旋翼的气动力和力矩，在体轴系中主旋翼的力可以表示为

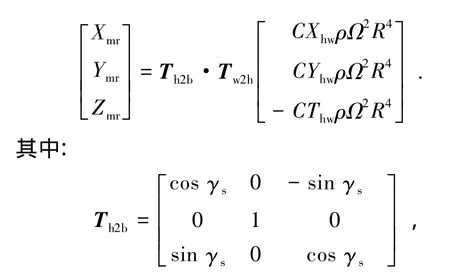
是体轴系与桨毂构造轴系的变换矩阵，γs为桨轴前倾角，Tb2h=Th2bT，是反变换矩阵;

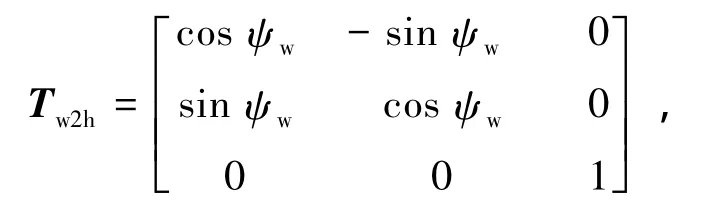
是桨毂构造轴系与桨毂风轴系之间的变换矩阵，ψw为旋翼侧滑角，Th2w=Tw2hT，是反变换矩阵;ρ，Ω，R分别为空气密度，旋翼转速和旋翼半径;CXhw，CYhw为旋翼旋转平面内力系数，其主要由旋翼升力与挥舞运动一阶谐波的乘积和旋翼型阻与诱导阻力构成，旋转平面内力可以近似为

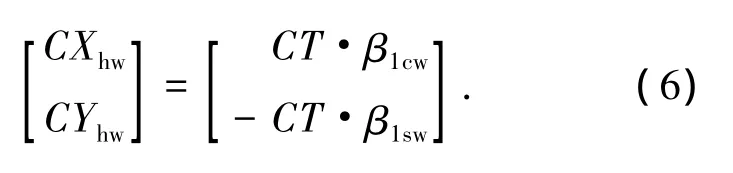
式中:β1cw，β1sw为风轴系旋翼挥舞角，CT为旋翼拉力系数.

旋翼的空气动力可以表示为

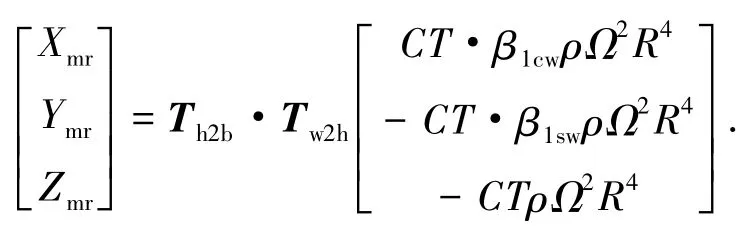
旋翼产生的空气动力力矩表示为

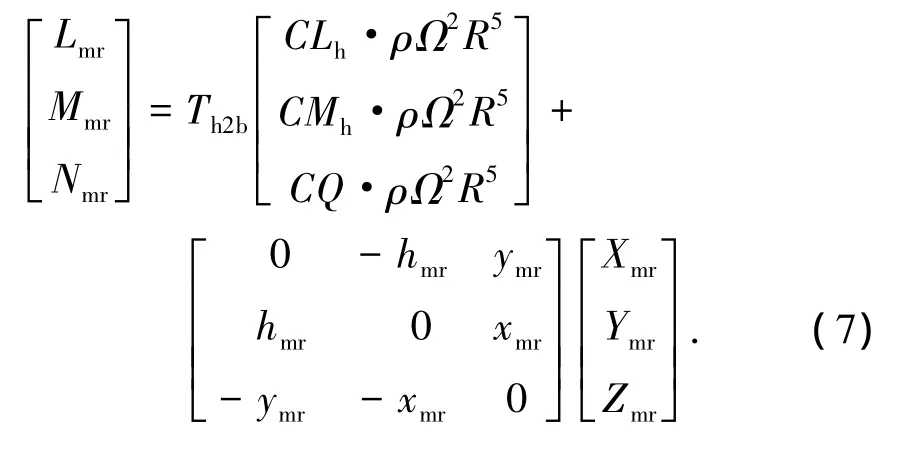
式中:xmr，ymr，hmr为旋翼位置坐标;CLh，CMh，CQ为在桨毂构造轴系内旋翼的滚转力矩、俯仰力矩以及扭矩系数，其中CLh，CMh主要由旋翼扭矩的贡献和旋翼刚度所引起的桨毂力矩两部分组成，第一部分是由于桨盘平面相对于旋翼轴的倾斜导致旋翼扭矩在滚转和俯仰方向产生投影，可以表示为

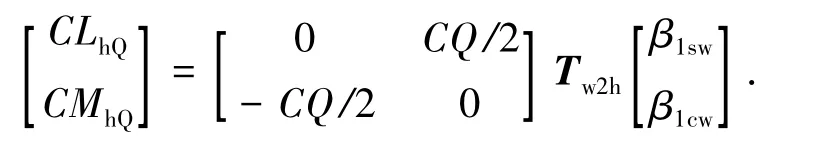
由于旋翼的刚度影响(挥舞角外伸)同样产生滚转、俯仰桨毂力矩，旋翼刚度引起的桨毂力矩可以表示为

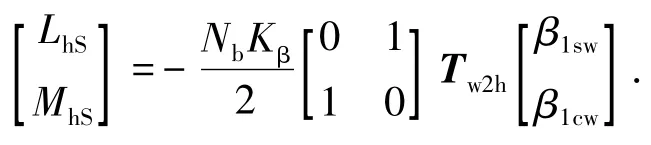
式中Nb，Kβ分别为桨叶片数和旋翼中心等效弹簧刚度.

根据主旋翼的空气动力和力矩，忽略尾桨挥舞，参考主旋翼的力和力矩，尾桨的力和力矩可以写为

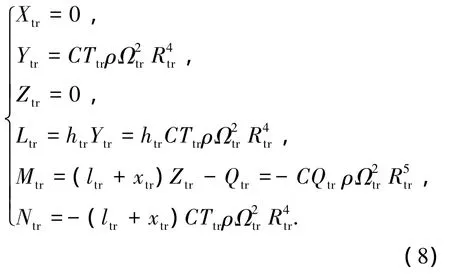
合并式(6)～(8)，得到主旋翼、尾桨的空气动力和力矩表达式，

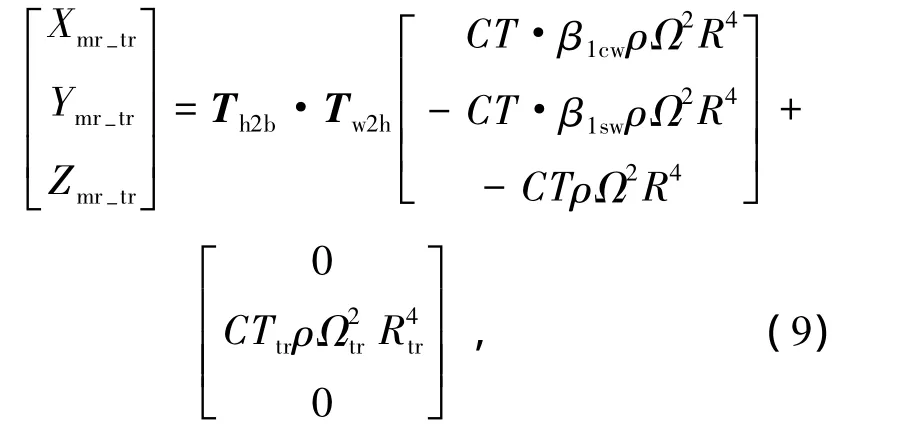
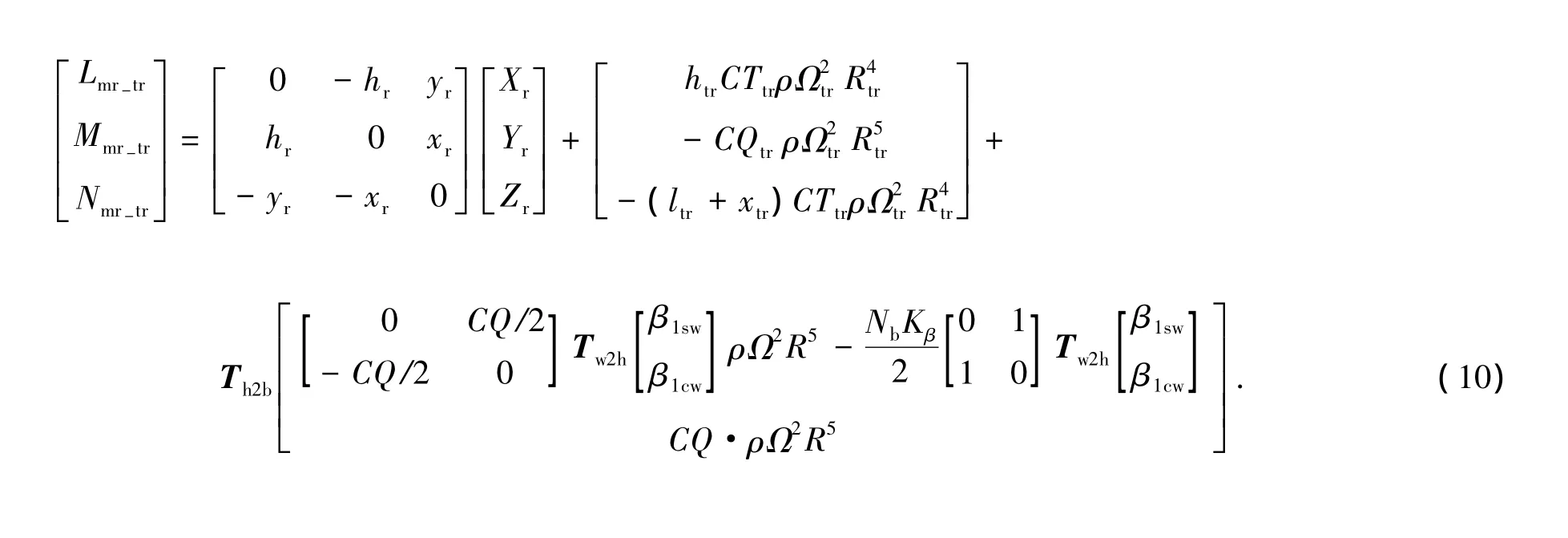
它们也是式(5)左侧的解析表达形式，由于式(5)的右侧已知，所以式(9)～(10)左侧已知.式(9)～(10)中并不显含控制输入，且未知数的数量大于方程的数量，对于控制量的求解既要保证精度，又要保证数值稳定性，因此在控制量求解过程中根据直升机自身飞行动力学的特点，规划控制量的求解方法.为了能够求解 θ0，θ1s，θ1c，θ0tr，其中的系数 CT，CQ，CTtr，CQtr，β1sw，β1cw，必须首先求解.根据式(9)中Zmr-tr的表达式，由主旋翼贡献，因此可以求出旋翼的升力系数CT，由CT可以求旋翼入流λ0，由旋翼入流可以求旋翼扭矩系数CQ，已知旋翼扭矩系数后，通过Xmr-trYmr-tr，获得˜β1sw˜β1cw的估计 值，根据 Nmr-tr求解CTtr，以此求解尾桨入流、尾桨的扭矩系数，通过Lmr-trMmr-tr求解β1swβ1cw的值，到此式(9)～(10)中系数都已可求解，再根据旋翼、尾桨空气动力模型求解 θ0，θ1s，θ1c，θ0tr.

1)旋翼入流.根据Zmr-tr的表达式，可以求解旋翼的升力系数CT，根据直升机前飞的动量理论，无量纲旋翼入流和旋翼的升力可以表示为

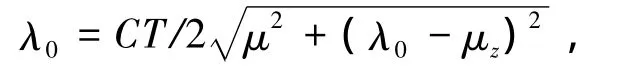
式中:μ =Vcos αd/ΩR，μz=Vsin αd/ΩR，αd为桨盘迎角，通过上式迭代求解即可得到旋翼入流.

2)旋翼扭矩.旋翼的扭矩通过对桨盘平面内的力进行积分获得，旋翼扭矩的表达式可以写为

式中CXhw可以通过式(9)的Xmr-tr来获得，通过CT可以求解CQ.

3)尾桨输入求解.当求得主旋翼的扭矩系数CQ后，根据式(10)中Nmr-tr的表达式，求解尾桨的拉力系数CTtr，类似于主旋翼入流的求解方法可求解尾桨的入流λ0tr.尾桨的拉力系数可以写为

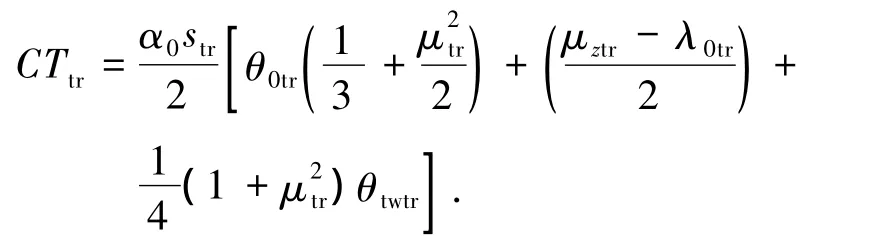
根据上式，尾桨的输入θ0tr可以求解得到，根据主旋翼的扭矩系数CQ的求解方法，求解尾桨的扭矩系数CQtr.

4)主旋翼输入的求解.最后通过式(10)中Lmr-trMmr-tr表达式，求解两个未知的旋翼挥舞系数β1sw和 β1cw，根据［β1sβ1c］T= Tw2h［1β1swβ1cw］T，将这两个挥舞系数变换到桨毂构造轴系中.联立旋翼的准定常挥舞运动方程和旋翼拉力系数方程，即可以求解旋翼的总距和纵、横向周期变距.挥舞运动方程以及旋翼的拉力系数方程可以表示为

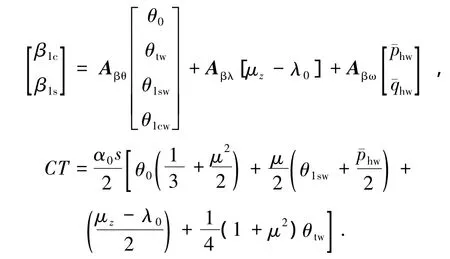
旋翼挥舞运动方程中的系数矩阵的具体形式可以参考文献［18］，通过上述的3个独立的线性方程组可以求解主旋翼在桨毂风轴系中的3个操纵量，利用 [ θ1sθ1c]T=Tw2h［θ1swθ1cw］T.将桨毂风轴系中的操纵量转换到桨毂轴系中，得到最终的旋翼操纵量.

3 显模型跟踪控制器结构

完成非线性逆动力学建模后，根据经典显模型跟踪控制律结构，吊挂系统中直升机的控制律结构如图6所示，由图可见控制器具备了可测量吊索力的处理能力.控制输入逆解实现了控制过程的近似线化，且能有效的处理可测量外部扰动.对于系统中的不确定性与外部扰动，进一步设计线性反馈控制器，则能进一步有效抑制外部干扰输入与系统不确定性，提高系统的稳定性.

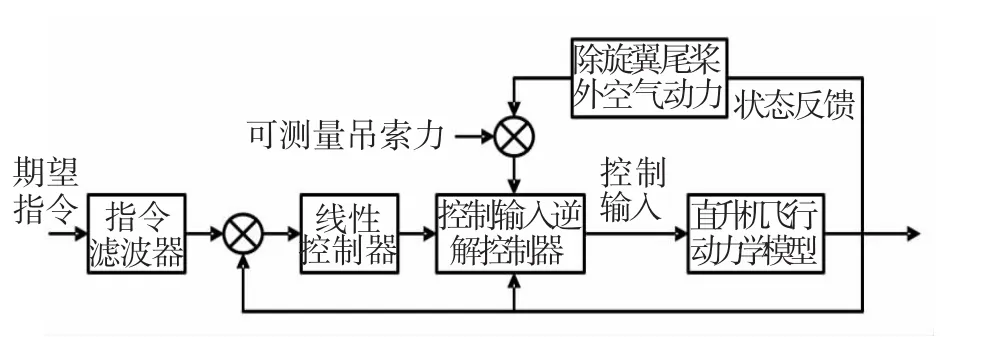
图6 直升机控制结构示意

4 数值仿真

4.1 与动态逆的比较仿真

建立非线性UH－60直升机飞行动力学模型，该模型采用动态入流理论，二阶旋翼挥舞动力学，模型的内部状态 21阶，包括 6个刚体自由度，3个姿态角，6个二阶挥舞状态，3个非均匀入流状态以及3个发动机状态，其空气动力学模型比本文控制输入逆解的空气动力学模型复杂.为了比较本文提出的控制律效果，针对单独的UH－60模型分别设计了动态逆模型跟踪控制律和基于控制输入逆解的非线性模型跟踪控制律，在无载荷情况下单独直升机的两种控制律仿真结果如图7～8所示，初始条件为悬停状态，控制模态为航向保持和三轴地速跟踪，0 s时刻给定北向速度跟踪为3.048 m/s，其他指令为零，两种控制律对于无吊挂单独直升机均能实现良好的控制品质.

图7 直升机姿态角响应

图8 直升机NED速度响应

在不改变两种控制律结构和参数的情况下，引入吊挂载荷构建四直升机协调吊挂非线性仿真系统，其配置形式如图1所示，每一架直升机的工作模态为航向保持和速度跟踪;四架直升机仿真初始值，与前面单机仿真初值相同，但是4架直升机在NED坐标下的位置初始值分别为:(0;0;0)，(0;30.48;0)，(30.48;30.48;0)和(30.48;0;0)，单位为 m;外挂载荷的重量为1 452 kg，位置初始值为平衡状态近似猜测值，其他状态为零;4架直升机的控制模态输入指令与单直升机仿真相同，分别给出了两种控制方案，仿真结果如图9～12所示.

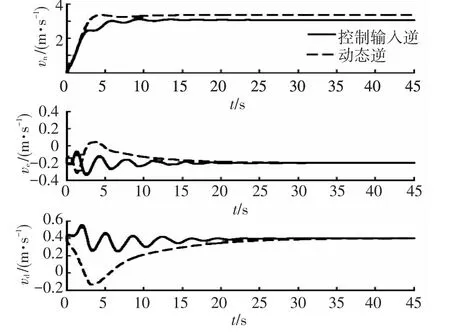
图9 直升机1NED速度响应

图10 直升机2NED速度响应

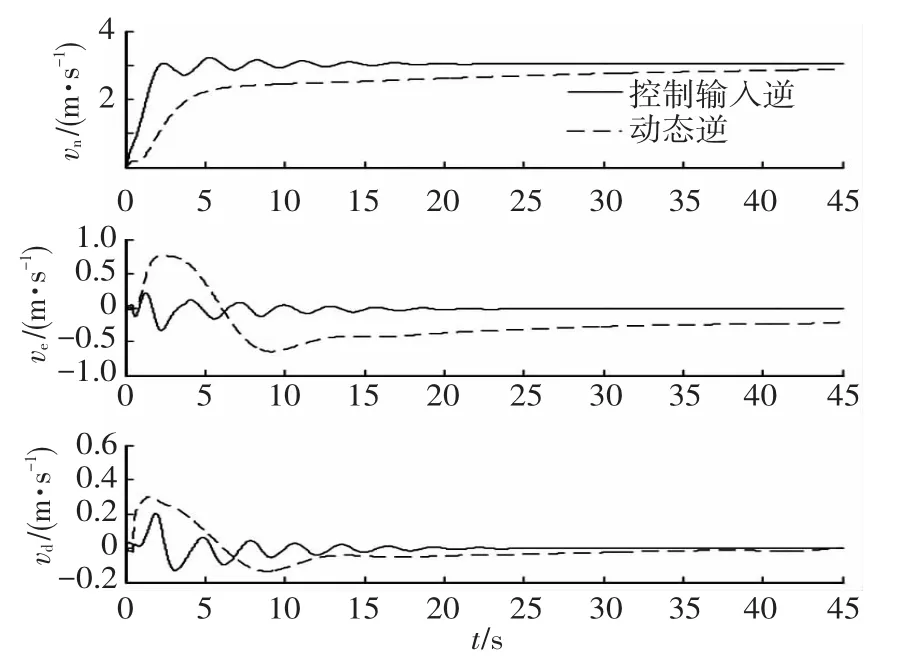
图11 直升机3NED速度响应

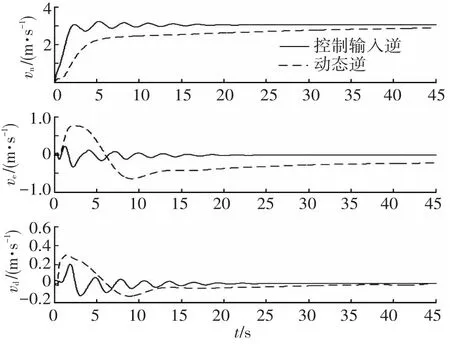
图12 直升机4NED速度响应

根据仿真结果可以看出，基于动态逆的控制效果比基于控制输入直接解控制器的效果差.在外载荷的影响下，基于动态逆的各个直升机速度跟踪性能不同，直升机1，2北向速度响应快于直升机3，4，且具有不同的稳态误差，吊挂载荷给直升机1，2提供了有利于指令方向的水平拉力，而对直升机3、4提供不利于指令实现的反向力，由于载荷施加给直升机的弹性侧向力和垂向力，导致直升机东向速度与垂向速度出现了低频的震荡调节，这直接造成四架直升机在相对位置的保持上出现了很大的误差，四架直升机在NED坐标下水平面相对位置见图13，四架直升机在水平载荷力的影响下无法保持编队飞行，坐标几乎重合到一起.而基于空气动力直接解的结果，因为采用了控制输入逆解，根据可测量的外部载荷直接计算得到控制量，有效消除了外载荷扰动，所有直升机无论是姿态还是速度的响应特性基本一致，四架直升机水平面相对位置见图14，仿真结束时四架直升机保持了良好的编队队形.

图13 动态逆4直升机水平面相对位置

图14 控制输入逆解4直升机水平面相对位置

4.2 鲁棒性能验证

外部吊挂载荷根据吊挂的货物不同重量会有很大的变化，以此对控制器的鲁棒性能提出了很高的要求，因此有必要考察控制器的鲁棒性能，将外部载荷由1 452 kg提高到13 608 kg，控制器的结构与参数不变，同时模拟四架直升机的角速率传感器测量噪声为有限带宽白噪声，幅值最大不超过0.2 rad/s.控制模态为速度保持配合协调转弯，首先给定所有速度为零，让系统自动寻找平衡点，紧接着给定垂直速度爬升，然后给定前飞速度保持并配合协调转弯完成期望轨迹.图15为吊挂系统的三维轨迹响应.图16为直升机地轴系速度响应.

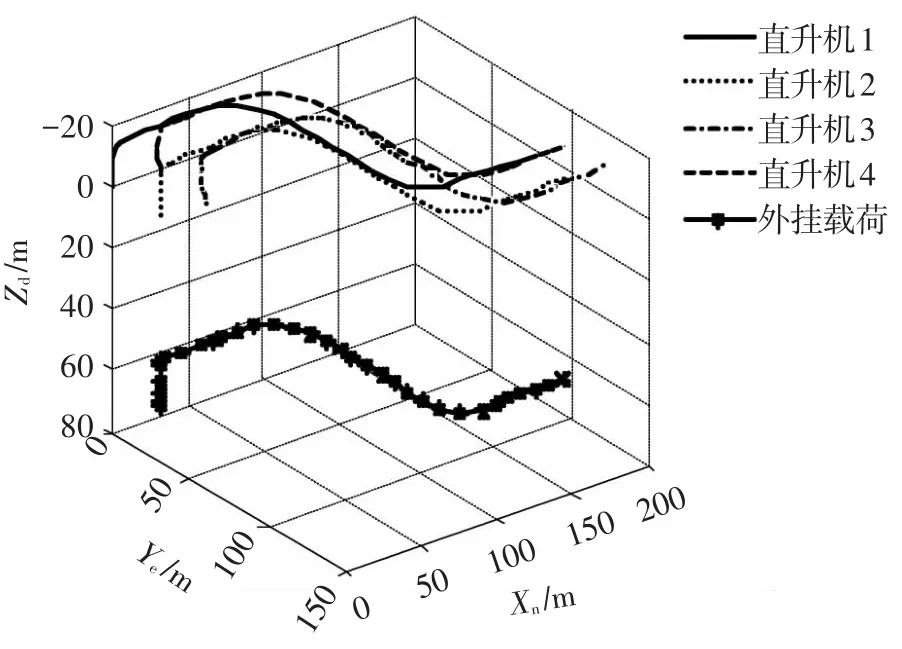
图15 协调吊挂系统三维位置响应

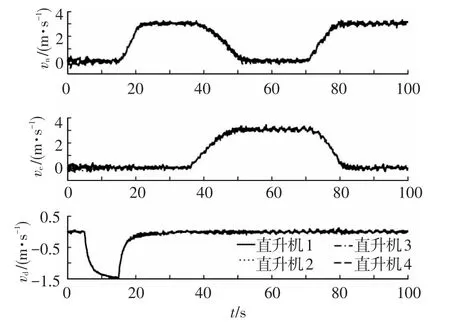
图16 协调吊挂系统直升机地速响应

由仿真结果可以看出即使载荷增加接近10倍且同时存在传感器噪声的情况下，系统依然能进行良好的速度跟踪，且比较好地完成了期望轨迹的跟踪，该仿真结果进一步证明了系统具有良好的鲁棒性.

5 结论

本文提出了基于空气动力学逆的控制输入直接解的非线性控制方法，通过仿真结果可以看出该方法的优越性体现在:

1)该方法可以将直升机这一复杂的飞行动力学系统转换为一个线性时不变系统，便于控制律设计.

2)该控制方法对于可测量的施加在直升机上的外力可进行直接反馈，用于期望控制输入的求解，从而能够保证协调吊挂系统中的每一架直升机都拥有一致的稳定性和响应性能，这一点对协调吊挂控制系统至关重要的.

3)建立了四直升机吊挂控制仿真系统，四架直升机具有相同的非线性控制器，即使在不同的载荷扰动下都表现了良好的控制性能，简化了控制律的设计，说明了方法的有效性.

［1］MEIER W H，OLSON J R.Efficient sizing of a cargo rotorcraft ［J］. Journal of Aircroft， 1988， 25(6):538－543.

［2］CURTISS H C，WARBUTON F W.Stability and control of the twin-lift helicopter system ［J］.Journal of the American Helicopter Society，1985，30(2):14－23.

［3］SHERIDAN P F. Feasibilitystudyformultiple helicopter heavy lift systems［R］.Philadelphia PA:Vertol Aircraft Corp，1957.

［4］CICOLANI L S，KANNING G.Equations of motion of slung load systems with results for dual lift［R］.Washington DC:NASA TM 102246，1990.

［5］MORTEN B，JAN D B，ANDERS C.Modeling of generic slung load system ［J］.Journal of Guidance，Control，and Dynamics，2009，32(2):573－585.

［6］HESS R A，TRAN P M.Pilot/vehicle analysis of a twin-lift helicopter configuration in hover［J］.Journal ofGuidance， Controland Dynamics， 1988， 11(5):465－472.

［7］PRASAD J V R，SCHRAGE D P，MITTAL M.Comparison of nonlinear controllers for twin-lift configurations ［C］//Proceedings of the AIAA Guidance，Navigation，and Control Conference.Boston，MA:［s.n.］，1989:1350－1357.

［8］RODRIGUE A A，ATHANS M.Multivariable control of a twin lift helicopter system using the LQG/LTR design methodology［C］//Proceedings of the 1986 American Control Conference. Seattle ［s.n.］， 1986:1325－1332.

［9］MENON P K A，PRASAD J V R，SCHRAGE D P.Nonlinear control of a twin-lift helicopter configuration［J］.Journal of Guidance Control and Dynamics，1991，14(6):1287－1293.

［10］MITTAL M，PRASAD J V R，SCHRAGE D P.Nonlinear adaptive control of a twin lift helicopter system［J］.IEEE Control Systems，1991，11(3):39－45.

［11］PRASAD J V R，MITTAL M，SCHRAGE D P.Control of a twin lift helicopter system using nonlinear state feedback［J］.Journal of the American Helicopter Society，1991，36(4):57－65.

［12］MEYER G，SU R，HUNT L R.Application of nonlinear transformations to automatic flight control［J］.Automatica，1984，20(1):103－107.

［13］HAMERS M，BOUWER G.Helicopter slung load stabilization using a flight director［C］//American Helicopter Society 61st Annual Forum Proceedings.Grapevine，TX:［s.n.］，2005.

［14］HAMERS M.Flight director for handling of helicopter sling loads［C］//31st European Rotorcraft Forum.Florence:［s.n.］，2005.

［15］BISGAARD M，COUR-HARBO A，BENDTSEN J D.Adaptive control system for autonomous helicopter slung load operations ［J］.Control Engineering Practice，2010，18(7):800－811

［16］BISGAARD M，ANDERSLA C.Input shaping for helicopter slung load swing reduction［R］.Reston，VA:AIAA，2008:2008－6964.

［17］IVLER C M，TISCHLER M B，POWELL J D.Cable angle feedback control systems to improve handling qualities for helicopters with slung loads［R］.Reston，VA:AIAA，2011:2011－6686.

［18］PADFIELD G D.Helicopter flight dynamics:the theory and application offlying qualitiesand simulation modeling ［M］. Washington: AIAA Inc，1996:87－186.

Model following nonlinear control of four helicopter slung load system

SONG Yanguo，WANG Huanjin

(College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，210016 Nanjing，China)

Multi-lift system control was researched based on control input inverse solution.In multi-lift system with slung load，every helicopter has different stability and response due to cable forces influence.It is very difficult to directly introduce cable forces feedback in controller design due to lack of explicit physical transformation from forces to actuators control.According to aerodynamics and flight dynamics，a nonlinear model following control scheme is proposed based on control inputs inverse solution.It is desirable to provide a high degree of stability augmentation for the multi-lift system by using direct cable forces feedback.The most significant improvement is that each helicopter in the multi-lift system has the same control structure and control law，which remarkably simplify design of controller and improve control performance.Controller’s performance is demonstrated in a nonlinear robust simulation.

multi-lift system;nonlinear control;model following;flight dynamic;slung load

V233.7;V212.4

A

0367－6234(2014)03－0066－08

2012－12－27.

江苏高校优势学科建设工程资助项目.

宋彦国(1973—)，男，副教授.

宋彦国，songyg@nuaa.edu.cn.

(编辑 张 宏)