轮式探测车被动自适应性与自由度关系分析

杨 飞，陶建国，邓宗全，黎佳骏

(1.机器人技术与系统国家重点实验室，150080 哈尔滨;2.哈尔滨工业大学机电工程学院，150001 哈尔滨)

轮式探测车被动自适应性与自由度关系分析

杨 飞1，2，陶建国1，2，邓宗全1，2，黎佳骏1，2

(1.机器人技术与系统国家重点实验室，150080 哈尔滨;2.哈尔滨工业大学机电工程学院，150001 哈尔滨)

为设计具有自适应性能的探测车，保证轮式探测车移动机构在行驶过程中车轮与地面接触良好，研究自适应性能与单侧悬架系统及其漫游车整体所需自由度之间的关系.给出自适应性的3种分类方法，分析自适应性能对漫游车的爬坡性能、车体稳定性能及能耗特性的影响;建立具有自适应性能的探测车单轮系统数学模型并得到此系统的自由度;分别建立包含两轮、三轮及k个车轮的自适应悬架系统数学模型，分析并得到上述系统所需的自由度;分别建立在悬架对称布置和四周布置两种情况下的探测车自由度模型，并对一些具有代表性的被动自适应特性探测车自由度进行了统计和分析.研究结果表明:良好的自适应性是实现移动机构综合性能的前提条件，具有自适应性的单侧悬架系统与探测车整体所需自由度分别为1和3.该方法可为探测车悬架及车体系统构型综合时自由度的确定提供指导.

探测车;被动自适应;轮式移动机构;自由度;悬架;构型综合

随着深空探测技术的发展，行星探测受到各个国家越来越多的关注，并掀起了新一轮深空探测热潮.行星探测车是对行星表面进行实地勘探的重要工具，是搭载各类科学探测仪器的平台［1］.未来的空间探测任务要求探测车能在预先未知或非结构化的环境中去执行任务.轮式探测车具有结构简单，质量轻，高效实用等优点，因此国内外行星探测车的研究以轮式为主［2－3］，特别是在崎岖地面上行驶的轮式行星探测车技术已经成为研究热点.

轮式探测车行驶过程中，各车轮与地面良好接触以保持均衡的牵引力是提高探测车综合性能的重要前提，这种性能被称为车轮对地面的自适应性.自适应理论应用极其广泛，其分类方法也多种多样.狭义地讲，从系统对外界输入有无反馈可将自适应分为3种类型.1)主动自适应:系统内部对外界环境的变化有反馈控制，使系统依据新输入而呈现出一种新结构、状态或功能，从控制角度讲，其是一个闭环控制.美国卡内基－梅隆大学研制的流浪者“Nomad”［4］，JPL 研制的 Nanorover等通过实时检测探测车的位置姿态，采用机电控制主动调节探测车的运动，获得最佳的行驶性能，均属于主动自适应探测车.2)被动自适应:系统在运行过程中不会对外界环境的变化有反馈，自身的状态也不会发生改变，是一种简单的输入输出关系，从控制角度讲，其是一个开环控制系统.美国喷气推进实验室(JPL)研制的“索杰纳”以及MER(mars exploration rover)探测车［5］，日本的Micro－5等［6］主要利用移动机构超静定特性实现轮系对地面的自适应，达到平顺车体、均衡牵引力的目的，均属于被动自适应轮式探测车.3)主、被动混合自适应:主动和被动自适应的有机结合，既有传感器和执行器保证相应的主动自适应控制，又有相应的被动自适应机构，如俄罗斯研制的Marskhold探测车既能被动适应地形又能主动适应地形，属于混合自适应探测车［7］.

探测车的自适应性与悬架的构型密切相关.被动自适应探测车虽只能适应一般复杂地形，但因其结构简单，能耗小，控制简单，可靠性高，因而在目前的行星探测中得到了广泛应用.基于地面自适应能力的轮式探测车构型综合能够使综合出的轮式探测车移动机构具有良好的地面自适应特性，从而保证探测车具有优异的运动学和动力学性能，但目前类似的研究文献还很少.

本文通过分析自适应性对移动机构性能的影响，研究具有良好被动自适应能力轮式探测车移动机构与其自由度之间的关系，为探测车的构型综合提供参考和借鉴.

1 被动自适应性与探测车性能关系

行星探测车的综合性能可通过一些子性能得到反映，如爬坡性能、稳定性及能耗特性等［8］.

1.1 爬坡性能

拥有良好自适应性能的探测车能保证每个车轮在爬越一定倾角的斜坡时与地面时刻接触，保证良好的牵引性能，使爬坡过程顺利进行.对于在行星上执行任务的探测车，探测车携带或能得到的能源有限，因此每个车轮电机能提供的功率也是一定的，则车轮能提供的最大驱动力矩为

式中:Fimax为作用在第i个车轮上的最大切向力，n为车轮总数，r为车轮半径，Tmax为全部车轮能提供的最大驱动力矩，Timax为每个车轮提供的最大驱动力矩.

如图1所示，当探测车爬越一定倾角斜坡且处于临界条件——所有车轮提供的驱动力矩恰好和车体重力沿斜坡的的阻力矩平衡时，若由于悬架等原因使某个车轮与地面脱离接触，这时其他车轮受到的阻力矩就会相应增加.由于电机能输出的驱动力矩有限，当驱动力矩小于阻力矩时就会导致探测车爬越斜坡失败.

图1 探测车爬越斜坡示意

1.2 车体稳定性

倾翻将造成探测车损坏，导致探测任务失败.探测车稳定性主要指移动机构抵抗倾翻的能力.零力矩点(zero moment point，ZMP)理论是判断系统稳定性的重要方法［9］.ZMP是指系统上与地面的一个接触点，其受到的地面反作用力绕该点的力矩分量在地面上的投影为0.根据ZMP理论，可将探测车行驶过程的稳定性表述为:若ZMP位于各车轮与地面接触点形成的支撑多边形之内，则探测车将不会发生倾翻.图2为一探测车ZMP示意图，P1～Pn为探测车n个车轮与地面的接触点，车体ZMP位于这n个点形成的多边形区域内.根据ZMP理论，在接触点形成的多边形区域内，稳定性与ZMP点所能移动的范围呈正比关系.若某些车轮与地面脱离接触从而使接触点形成的多边形面积减小，就会减小ZMP点的移动范围，其稳定性就会相应地下降.图2(b)中两车轮与地面脱离，假设在多边形中代表这两车轮与地面的接触点为P3和P4，则新形成的稳定区域就会比图2(a)所示的区域减小，这时ZMP点能移动的范围减小，车体的稳定性就会下降.因此车轮与地面时时接触是保证车体稳定性的重要条件.

图2 探测车零力矩点示意

1.3 能耗特性

影响移动系统能耗特性的直接因素有机械系统传动效率、电机效率及车轮与地面的滑转等.探测车在运动过程中姿态不断发生变化，车轮载荷也不断发生变化，会造成车轮滑转率不同，车轮前进速度产生差异而造成能量的内部损耗.因此，车轮滑转率对能耗有很大影响，可将其作为一个评价指标.滑转率表示为［10］

式中:Sf为车轮实际行驶距离，S为车轮理论行驶距离.

当车轮与地面接触减少或发生空转时，都会使Sf减小甚至为0，这将导致车轮滑转率增大，增大移动系统的能源消耗.因此，应保证车轮能很好地自适应行驶，使各轮重力分配均匀，避免车轮悬空现象发生，以减小车轮滑转率，减少不必要的能耗.

2 被动自适应探测车所需自由度分析

2.1 被动自适应移动机构单轮系统自由度分析

在移动系统行驶的每一时刻，可将车轮与地面视为点接触.在非结构化环境中，若不考虑主动转向运动且两边车轮没有速度差，将车轮与地面离散的接触点连起来形成一条接触曲线，则此接触曲线为某一地形剖平面内的轨迹曲线，如图3中曲线S1所示.

图3 单轮系统运动示意图

为使车轮对地面具有良好的自适应性能，则车轮应时刻与地面发生接触，那么曲线S1是车轮在不同位置下的包络线，r为S1的径矢，设包络曲线S1的方程为

且其上无奇点，即rx×rz≠0.因曲线S1是车轮在不同位置的包络线，所以P点也是车轮轮廓线上的点，这时P点在曲线S1和车轮轮廓线上的切矢应相等，即

令S1=f(x，z)，Δxi=Δxi-1+Δx，Δzi=Δzi-1+Δz，(i=1 ～ n)，其中Δx、Δz为在相等的时间间隔内在x、z方向上的增量，那么弧线S1的偏导矢可以表示为

若将轨迹曲线在x和z两个方向上进行分解，则相等的时间内在x方向上行驶的距离是相等的，即Δx=0.但由于起伏的地形，相等的Δx值对应不同的Δz值，因此

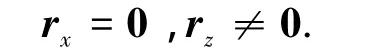
当车轮匀速行驶在起伏路面上时，主要适应z向地形变化即可，这时单轮系统仅需一个自由度.

2.2 被动自适应移动机构整体自由度分析

查阅相关文献可发现，很多已经成功应用或正在研制当中的轮式探测车移动系统多为两侧或四周布置形式.两侧布置移动机构一般为悬架系统的左右对称布置，如“索杰纳”行星探测车;移动机构四周布置形式较复杂，其车轮－悬架系统与载荷平台连接方式为铰接或差动与铰接的混合连接，如Micro－5为全铰接形式，而文献［11］所述探测车则为差动与铰接的混合连接.

2.2.1 单侧车轮－悬架系统自由度分析

图4所示为车轮连接的基本单元——两个车轮连接的情况.

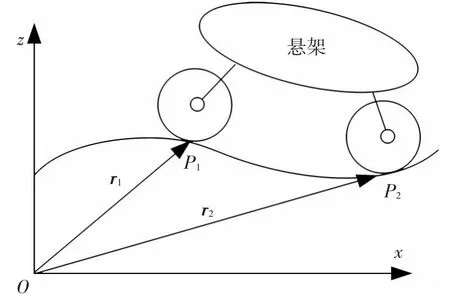
图4 车轮-悬架连接单元示意

两车轮分别与悬架连接，但具体连接由于不同的探测车悬架结构不同，在此不具体确定.悬架的作用是保证两车轮满足被动自适应性所需的自由度.设两车轮当前位置与地面接触点分别为P1、P2，对应的径矢分别为 r1、r2.

若车轮有高度差，径矢r1，r2在z向的分量有如下两种关系:

1)当|r1z|＞|r2z|，表明两车轮在z向有高度差，如图5(a)所示.当车体沿箭头方向行驶且把车轮2的z分量视为参考值时，可假设移动机构正在对高度为h=|r1z|-|r2z|的障碍进行越障.对于此时的车轮-悬架系统，可将其认为是一个被动的分时自适应系统，即在某一时刻只有一个车轮的相对高度发生了变化，而另一车轮保持原状态不变，则两车轮之间只需一个相对自由度来适应z向的变化，即悬架系统需提供一个自由度.

2)当|r2z|＞|r1z|，其越障如图5(b)所示.箭头指示探测车行驶方向，障碍高度h=|r2z|-|r1z|，分析过程与1)类似，即悬架系统只需提供一个自由度.

图5 两车轮相对高度变化示意

由上述分析可知，基本的车轮－悬架单元具有被动自适应性的前提是此系统具有一个自由度.大多数探测车单侧悬架连接的车轮数一般≥2，因此有必要对车轮数大于两个的车轮－悬架系统自由度进行研究.

设A、B、C、D、E代表单侧车轮 -悬架系统连接的5个车轮，且令A∩B=1表示车轮A与B之间有一相对自由度，其余类推.若车轮 -悬架系统具有被动自适应性，则各车轮之间有相对的自由度，可自动适应地形起伏变化.以A为例，若其被动自适应性不受其他车轮干涉，即在运动过程车轮A与其他车轮之间都有相对的自由度，即

由分析可知，当车轮 -悬架系统为两轮基本单元时，可保证每一时刻两轮之间总有相对的自由度，且此系统的自由度为1.因车轮A要同时与车轮B、C、D、E在运动时有相对的自由度，则A可与B、C、D、E组成两轮基本单元系统，即

式中:F=B∪C∪D∪E，车轮B、C、D、E组成一个系统F.

则车轮A与车轮系统F组成的车轮-悬架系统自由度为1.对于车轮B，因要具有被动自适应能力，除了A∩B=1，B∈F外，还必须满足

则同理B∩G=1.

式中:G=C∪D∪E，车轮C、D、E组成一个系统G，且 G ⊂ F.

车轮B与新系统G为具有被动自适应性能的基本两轮单元系统，此时系统的自由度为1.同理，车轮C、D、E也可以做类似的分析，得出类似的结论.

分析了可分解为两轮基本单元的车轮－悬架系统自由度为1的充分性后，下面分析其必要性，即从最基本的两轮单元系统来分析整体系统的自由度.图6为单侧车轮－悬架系统基本两轮单元连接示意图.设有 n个车轮，分别为1，2，…，n，各两轮基本单元通过转动副 J1，J2，…，Jn-1连接.因其为平面机构连接，可用下式计算其自由度:

式中:F为平面机构的自由度，n为总的构件数，包括一个地面，p为平面低副数目，设车轮与地面间为纯滚动，即视为低副.

轮式漫游车悬架有不同的构型，悬架在空间上有不同的布置形式，如两侧对称式、四周均布式、三点铰接式等等.虽然布置方式不同，但从目前已有的漫游车布置方式来看，每侧悬架与载荷平台都为点连接即各个独立的悬架都只有一个输出，要求悬架能提供一个输出自由度.如图6(a)、(b)所示分别为连接两个车轮与3个车轮的悬架示意图，悬架的具体结构及连接方式未知.

若要使综合出的悬架对崎岖地面具有被动自适应性，对于两轮或三轮悬架来说，其必须满足下列条件:

1)悬架在任意工况下都必须满足因崎岖地面导致的车轮对悬架的输入自由度;

2)在任意工况下，悬架的输出自由度不应被干涉，即悬架必须满足对载荷平台的这个输出自由度.

综上，对于具有被动自适应性能的两轮悬架而言，其必须时刻能提供3个自由度.因悬架为平面机构且与载荷平台为点连接，不存在作为机架的杆件，因此其杆件数和运动副数满足下式:

图6 双轮及三轮单侧悬架系统

同理，对于单侧三轮悬架，其杆件数和运动副数满足下式:

两轮悬架-车轮系统中，在计算整体系统的自由度时除悬架所含的杆件和运动副外，还应包括车轮、地面及其之间相互连接的运动副，即还应加上n1=3的杆件及p1=4的平面低副.但应注意的是在车轮-悬架系统中，地面是不动的，被当作机架看待，由式(1)可得整体系统的自由度为

同上，在三轮悬架－车轮系统中，除悬架所含的杆件和运动副外，还应加上n1=4的杆件及p1=6的平面低副，结合式(2)可得整体车轮-悬架系统的自由度为

同理，对于单侧有k个车轮的悬架系统，其单侧悬架须提供k+1个自由度，即

当分析车轮-悬架系统的自由度时，还应加上n1=k+1的杆件及p1=2k的平面低副，则整体系统的自由度为

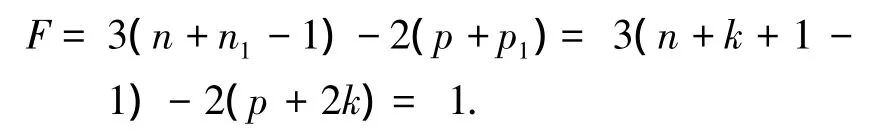
由以上分析可知，对于一个具有被动自适应性能的车轮－悬架系统，为保证每时每刻车轮之间都有相对的自由度来适应地形的变化，无论连接方式多么复杂，具有被动自适应性能的车轮－悬架系统所需自由度为1.

2.2.2 移动系统整体自由度

本文所述探测车系统自由度是其被动适应地形所具有的自由度，不包括由于主动控制而引入的自由度，例如车轮转向电机引起的转向自由度.对于移动系统自由度，不同文献有不同计算方法，如在文献［8］、［12］中移动系统自由度为所有运动副自由度的代数和，这就造成了不同车型根据不同方法计算后其自由度有差异.从构型角度考虑，为寻找其自由度的规律，应以普遍的计算机构自由度的方法来计算整车自由度.

假设移动系统行驶在平坦地面上且车轮与地面之间为纯滚动，这时各悬架与载荷平台的铰接轴为输入，载荷平台的位姿变化为输出.当各铰接轴之间无相对高度变化时，移动系统有最少的自由度，即由于车轮转速不同而引起的车体绕垂直于地面坐标轴的转动以及沿地面的两个平动，共3个自由度.

移动系统实际结构及连接方式复杂多样，但其系统自由度可通过下式计算［13］:

式中:fi为第i个运动副的自由度数;N为运动副数;λ为闭合约束数，对于空间封闭链，λ=6，对于平面封闭链，λ=3;L为封闭链数目.

2.2.2.1 两侧布置移动系统自由度分析

从目前已有的探测车移动系统可发现，两侧布置的车轮－悬架系统与载荷平台一般通过差动装置连接，如此可很好地平衡两侧悬架输入的不同俯仰角对载荷平台的影响.差动装置输出的相对自由度为1，可表达为

设移动系统由左右对称的车轮－悬架系统与载荷平台组成，由前述分析可知，具有被动自适应车轮－悬架系统自由度为1，即

则移动系统的自由度为

由此可见，单侧车轮－悬架系统自由度为1，左右对称与载荷平台差动连接的移动系统自由度为3.构型综合时，选择车轮－悬架系统自由度为1，移动系统自由度为3，如此在同等条件下可减少所用杆件数量，从而减少系统复杂性及车体质量，这可以从已经研发出的大多数探测车上得到体现.

2.2.2.2 四周布置移动系统自由度分析

四周布置移动系统车轮－悬架系统与载荷平台的连接具有结构和数量不规律的特性，这样可使移动系统某方面的性能更突出，因此其自由度往往≥3，其车体系统自由度计算可通过式(3)计算.

图7为尚建忠等［14］提出的一种三摇臂移动系统，侧摇臂的转动副轴线均与y-z平面垂直，而在尾摇臂的所有转动副中，悬架与车轮铰接的轴线与y-z平面垂直，悬架与载荷平台铰接的轴线与x-y平面垂直.因此，悬架、车轮与地面形成的闭链数目L=3，且平面闭链λ1=3，λ2=3，形成的空间闭链λ3=6，则车体系统自由度为

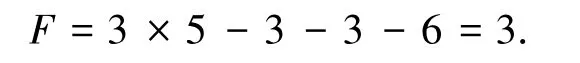
在进行自由度计算时，运动副数目要包括不同车轮与地面接触所形成的接触副.当车轮运时，转向电机动作而使车轮具有的转向自由度不在被动适应范围之内，因此车轮与地面接触副看作具有一个自由度的运动副［11］.

图7 六轮三摇臂悬架探测车

3 一些常见被动自适应移动系统属性

在移动系统的研究中，自适应性能是一个重要的性能指标.主动自适应因控制较复杂，还未得到广泛应用，却是未来的发展方向.表1是一些有代表性的、常见移动系统的相关属性.从表中可看出，具有被动自适应性能的移动系统，其单侧车轮－悬架系统通过合理连接后，自由度以1为主，整车系统的自由度以3为主，但为使某方面的功能得到加强，可增加相应自由度，使整体自由度＞3.这些信息有助于指导设计者从自由度的角度对移动系统进行相应的构型综合.

表1 一些常见被动自适应移动系统及其相关属性［6，15，16］

4 结论

1)分别分析了被动自适应特性与移动系统各主要性能之间的关系，得出车体良好的被动自适应性是实现移动系统综合性能的基本前提.

2)以良好的被动自适应为条件，对单轮系统进行了建模分析，进一步研究了移动系统单侧车轮－悬架系统所需要自由度，并给出了相应的证明.

3)以单侧车轮－悬架系统为基础，研究移动系统整车自由度，对一些已研发的具有被动自适应性移动系统自由度进行统计，发现对称的单侧车轮－悬架系统自由度一般为1，而整车系统自由度以3为主.

4)研究具有被动自适应性能移动机构尤其是单侧车轮－悬架系统结构与自由度之间的关系，为构造新型的具有被动自适应性能的探测车提供了借鉴和理论参考.

［1］GU Kanfeng，WANG Hongguang，ZHAO Mingyang.The analyse of the influence of external disturbance on the motion ofa six-wheeled lunarrover［C］//Proceedings of 2007 IEEE International Conference on Mechatronics and Automation.Harbin:IEEE，2007:393－398.

［2］CHEN Baichao，WANG Rongben，JIA Yang，et al.Design of a high performance suspension for lunar rover based on evolution［J］.Acta Astronautica，2009，64(9/10):925－934.

［3］SIEGWART R，LAMON P，ESTIER T，et al.Innovative design for wheeled locomotion in rough terrain，robotics and autonomous systems［J］.Robotics and Autonomous Systems，2002，40(2/3):151－162.

［4］ROLLINSE，LUNTZJ， FOESSELA. Nomad:a demonstration ofthe transforming chassis［C］//Proceeding of IEEE International Conference on Robotics and Automation.Leuven，Belgium:IEEE，1998:611－617.

［5］LINDEMANN R A，BOCKLER D B，HARRINGTON B D， et al. Mars exploration rover mobility development［J］.Robotics ＆ Automation Magazine，IEEE，2006，13(2):19－26.

［6］KUBOTA T，KURODA Y，KUNII Y，et al.Small，light-weight rover“Micro5”for lunar exploration［J］.Acta Astronautica，2003，52:447－453.

［7］陶建国.串联多关节悬架六轮月球车移动系统及其关键技术研究［D］.哈尔滨:哈尔滨工业大学机电工程学院，2009:8.

［8］尚建忠，罗自荣，张新访.基于构型的轮式空间探测机器人创新设计与优化［J］.中国机械工程，2007，18(4):414－417.

［9］罗昌杰，邓宗全，刘荣强，等.基于零力矩点理论的腿式着陆器着陆稳定性研究［J］.机械工程学报，2010，46(9):38－45.

［10］MALENKOV M I.Key technologies of the moonexplorationrealization and perspectives ofcreation ofhighly effective locomotion systems for the moon rovers［C］//Proceedings of 8th ILEWG conference on exploration and utilization of the moon. Beijing:IEEE，2006:23－27.

［11］SINGH A K，EATHAKOTA V P，KRISHNA K M，et al.Evolution of a four wheeled active suspension rover with minimal actuation for rough terrain mobility［C］//Proceedings of the 2009 IEEE International Conference onRoboticsand Biomimetics.Guilin:IEEE，2009:794－796.

［12］ROONEY J，HOBBS J D.Towards kinematic classification schemes for planetary surface locomotion systems［J］.Mechatronics，2003，13(2):153－174.

［13］BARLAS F.Design of a mars rover suspension mechanism［D］.Turkey:Izmir Institute of Technology Izmir，2004:23－24.

［14］尚建忠，罗自荣，张新访.两种轮式月球车悬架方案及其虚拟样机仿真［J］.中国机械工程，2006，17(1):49－51.

［15］THUEER T，LAMON P，KREBS A，et al.Crab-exploration roverwith advanced obstacle negotiation［C］//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems.Beijing:IEEE，2006:4260－4263.

［16］THUEER T， KREBS A， SIEGWART R.Comprehensive locomotion performance evaluation of all-terrain robots［C］//Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems.Beijing:IEEE，2006:4260－4265.

Relationship analysis between passive self-adaptability and degrees of freedom of the wheeled rover’s locomotion system

YANG Fei1，2，TAO Jianguo1，2，DENG Zongquan1，2，LI Jiajun1，2
(1.State Key Laboratory of Robot Technology and System，150080 Harbin，China;2.School of Mechatronics Engineering，Harbin Institute of Technology，150001 Harbin，China)

To make the designed rover have self-adaptability and better contact with ground，DOFs required for single suspension system and the whole rover are studied.Three classification ways of self-adaptability are given，and the relationship between self-adaptability and climbing performance，stability，energy consumption is analyzed.Mathematic model of single wheel-suspension system is established and such system’s DOF is obtained.Based on aforementioned analysis，mathematic models of double，three and k wheel-suspension system are established respectively with calculated DOFs for these systems.Two DOF models for wheeled rover are given followed by DOF statistics and analysis of some representative self-adaptive rovers.The analysis shows that self-adaptability is the basis for realizing comprehensive performance of the locomotion mechanism.DOFs for single suspension system and rover are 1 and 3，respectively.The conclusion has universalism and can determine required DOFs for structural synthesis of wheeled rover.

rover;passive self-adaptability;wheeled locomotion mechanism;DOF;suspension;structural synthesis

TH122

A

0367－6234(2014)03－0030－07

2013－03－30.

高等学校学科创新引智计划资助项目(B07018);

国家自然科学基金资助项目(51075079).

杨 飞(1985—)，男，博士研究生;陶建国(1964—)，男，教授，博士生导师;

邓宗全(1956—)，男，教授，博士生导师.

陶建国，jgtao@hit.edu.cn.

(编辑 杨 波)