深空通信系统中高阶LDPC码的软定时同步算法

周相超，赵旦峰，薛 睿

(哈尔滨工程大学信息与通信工程学院，150001 哈尔滨)

深空通信系统中高阶LDPC码的软定时同步算法

周相超，赵旦峰，薛 睿

(哈尔滨工程大学信息与通信工程学院，150001 哈尔滨)

深空通信具有信号衰减严重，接收机信噪比低的特点，针对深空通信系统中高阶LDPC码定时同步实现困难的问题，提出一种码辅助定时同步算法.首先使用高阶LDPC码的译码软信息构造一种代价函数，进行大定时偏移的粗同步，其次基于最大似然准则，使用EM算法进行定时偏移的细同步.该算法将定时同步器、解调器与译码器联合迭代，利用高阶LDPC译码器输出的软信息辅助定时同步，并通过数字插值方式对过采样信号进行补偿，从而得到接近修正克拉美罗限的定时估计.仿真结果表明，在低信噪比条件下，算法能够在较大定时偏移范围内实现有效的定时同步，并以较低的复杂度获得近似理想的系统误码率性能.

定时同步;高阶LDPC码;码辅助;译码软信息;深空通信

自LDPC码被重新发现以来［1］，因其接近香农限的高编码增益，目前广泛应用于移动通信、深空通信等领域［2］.与二元 LDPC码相比，高阶域LDPC码本身存在消除小环的潜力，具有更强的抗突发错误能力，并能够更有效地同高阶调制技术结合从而提供更高的数据传输速率和频谱效率，因此近年来高阶LDPC码逐渐成为信道编码领域的研究热点［3］.

在数字通信系统中，定时同步是保证信息可靠传输的重要基础.目前，数据辅助(Data-aided，DA)和非数据辅助(Non-data-aided，NDA)是传统定时同步的两种主要方法，DA方法通过发送训练序列可以获得较为理想的定时同步，但存在频带利用率和功率利用率低的缺点;NDA方法采用盲估计的方式获得定时偏移的估计值，但是在低信噪比条件下定时精度很差.因此，对于高阶LDPC编码系统而言，如何在低信噪比条件下获得精确的定时同步是需要解决的技术难题.

近年来，国内外兴起了一类新的码辅助同步算法，用于研究低信噪比条件下Turbo码、二元LDPC码的信号同步问题，能够达到精确较高的定时估计.文献［4］基于EM算法提出迭代定时估计方法，定时偏移由Turbo译码器输出的软信息辅助估计，其估计精度较高，但是存在局部最优点的问题，无法实现较大同步偏移的估计.文献［5］基于二元LDPC码的密度进化理论构造译码软信息的均值，使用过采样和插值方式进行定时同步，其同步效果较为理想，但是也存在同步范围较小的问题.文献［6］针对Turbo码，提出以软信息平方和为代价函数的同步方法，由同步参数的二维搜索获得精确的估计值，但算法存在实时性差的严重问题.文献［7］提出基于二元LDPC码软判决度量的同步方法，通过搜索窗获得定时偏移的最佳估计值，其同步范围较大，但是实时性较差.文献［8］针对二元LDPC码，利用译码软输出均值进行定时粗同步，并基于简化的EM算法进行定时细同步，从而获得较为理想的定时补偿，但是算法的复杂度很高.文献［9］基于最大似然准则，将码辅助同步与导频有机结合，可以获得同步精度和同步范围均良好的同步算法，但是会降低系统的频带利用率.

针对具有低信噪比的深空通信系统，借鉴现有的Turbo码和二元LDPC码的同步算法，提出一种适用于高阶LDPC码的定时同步算法.该算法基于联合迭代算法的思想，构造基于软判决信息的定时偏移代价函数，并依据最大似然准则进行低信噪比条件下高阶LDPC码的定时同步.仿真结果表明，本文所提算法的定时同步精度较高，能够接近修正克拉美罗限，与现有的同步算法相比，具有更大的定时同步范围.

1 高阶LDPC码的系统模型

高阶LDPC码的系统模型如图1所示，信道编码使用高阶LDPC码，调制方式采用阶数为16的16QAM调制，信号的传输信道设定为深空通信系统中最常用的高斯白噪声信道(AWGN)，信道的双边功率谱密度设定为N0/2，在图1的系统模型上进行算法推导和系统仿真.

发射机输出的基带信号可表示为

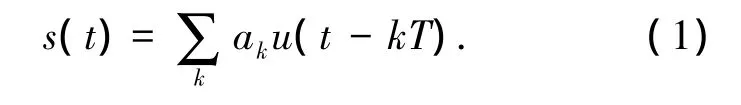
式中:ak为16QAM符号，T为码元周期，u(t)为单位能量的平方根升余弦脉冲，滚降系数为α.

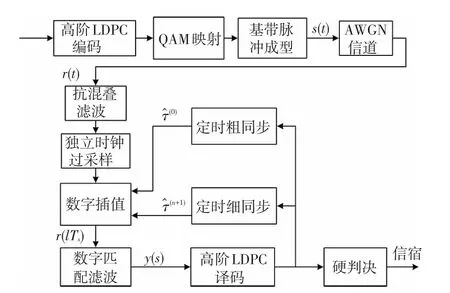
图1 高阶LDPC码系统模型

假定接收机已获得理想的载波同步、帧同步，且码间干扰可忽略，则信号经AWGN信道的传输延时τ，接收机输入的基带信号表达式为

式中:n(t)是零均值复高斯白噪声，其同相分量与正交分量相互独立，方差为N0/2.

高阶LDPC码是一种具有稀疏校验矩阵的线性分组码，与二元LDPC码相比，具有更好的误码率性能，抗突发错误能力更强，并适于与高阶调制结合.高阶LDPC码的译码以BP类算法为主，采用运算复杂度较低的FFT－BP算法进行译码［10］.在高阶LDPC码迭代译码时，译码器输出码元符号的后验概率为

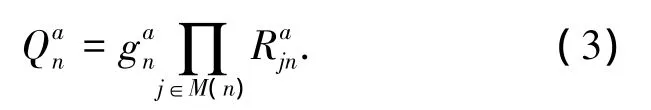
文中所提的码辅助定时同步算法中，高阶LDPC译码器输出的码元后验概率将分别用于定时粗同步和细同步，随解调器、译码器、定时同步器的联合迭代，最终获得较可靠的定时估计.

2 软定时同步算法

2.1 定时偏移的最大似然估计

最大似然估计是信号检测与估计的最佳准则，依据该准则，可以获得理想的定时偏移估计性能.

基于最大似然准则的定时估计可表示为

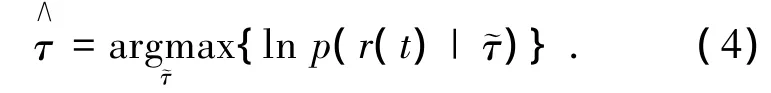
式中:ln p(r(t)|τ)为定时偏移τ的对数似然函数.

为了求解式(4)，对对数似然函数ln p(r(t)|τ)求偏导并令其为零，即

可得定时偏移的最大似然估计值，但是在数学上，式(5)存在解析求解困难的问题，因此需要采用其他方法去近似最大似然估计.

2.2 码辅助定时粗同步

定时粗同步主要完成定时偏移范围较大的同步，并给定时细同步提供初始补偿.在高阶LDPC编码系统中，因非理想的定时同步导致译码器输出码元概率的可靠性严重下降，各码元的后验概率趋于均匀分布，导致译码器输出对数似然比接近于零，借鉴文献［6］的思想，针对定时偏移，通过对一帧数据的对数似然比取均值，提出基于高阶LDPC码译码软信息的代价函数，其表达式为

式中:K为一帧数据的长度，L(k)为译码器输出的对数似然比，不同定时偏移对应不同的代价函数值，此代价函数是判断定时同步与否的有效标志.

图2显示的是在归一化信噪比Eb/N0为3 dB时，归一化代价函数随定时偏移τ的分布情况.由图2可得:在理想定时同步区域内，即τ=0时，归一化MSSO具有最大值，随定时偏移的增大，归一化MSSO逐渐减小.

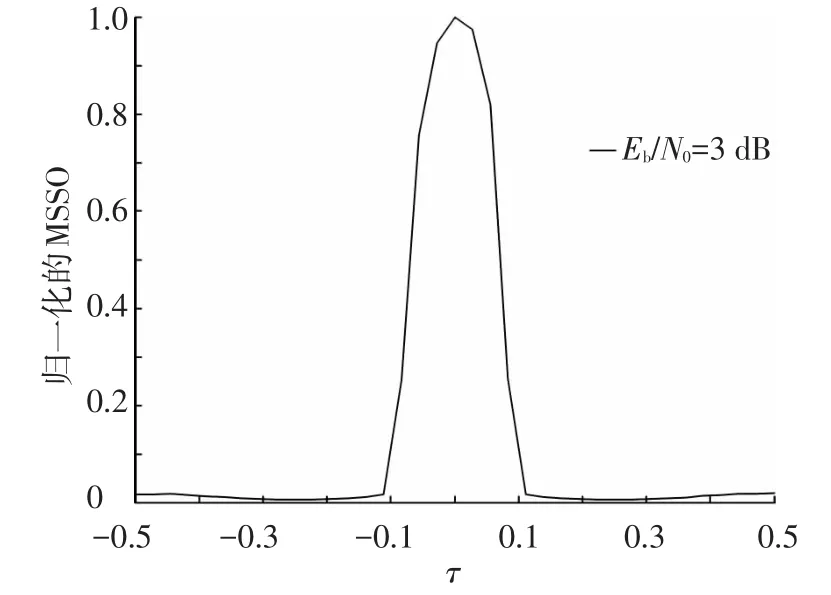
图2 归一化代价函数分布图

通过在定时偏移空间里穷举搜索使MSSO取得最大值的定时偏移量，即可实现定时同步，但是当定时偏移较大时，穷举搜索计算复杂度和延时很大，不适于工程实践，为此，对搜索算法进行改进，只将代价函数用于大定时偏移范围的粗同步，通过有限次数的搜索、补偿，将大定时偏移缩小至较小范围.

图1所示的系统框图中，高阶LDPC码系统的定时粗同步实现结构如图3所示，其中，归一化定时偏移τ的范围设定为［-1，+1］，分别将τ设置为τ(0)=-0.5、τ(0)=0、τ(0)=0.5，进行3次预补偿，通过选择MSSO最大值对应的定时偏移量即可获得定时粗同步值(0).

经过定时粗同步的补偿，接收机的定时偏移被局限于［－0.25，+0.25］的范围之内，为定时细同步提供良好的初始化条件.

图3 定时粗同步的结构图

2.3 码辅助定时细同步

图1的系统框图中，接收机输入信号r(t)经4倍信号过采样并经定时粗同步补偿之后可表示为

式中:Ts为采样周期，τ'为定时粗同步之后剩余的定时偏差.由此，数字匹配滤波器的输出为

因最大似然估计存在求解困难的问题，借鉴文献［4］的思想，基于EM算法使用迭代的方式进行定时细同步.EM算法包括E步骤和M步骤，经过E步骤和M步骤的多次迭代，可获得未知参数的近似最大似然估计值.

由EM算法［11］，设过采样信号向量r为非完整数据集，z=［r，a］为完整数据集.在E步骤中，构造定时偏移τ'的Q函数:

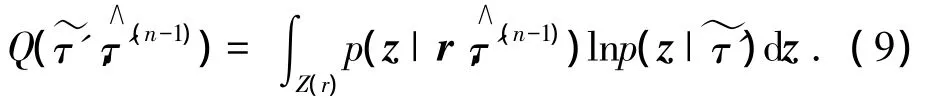
M步骤用于获取新的定时偏移估计值:

由 z=［r，a］，可对 Q 函数进行化简

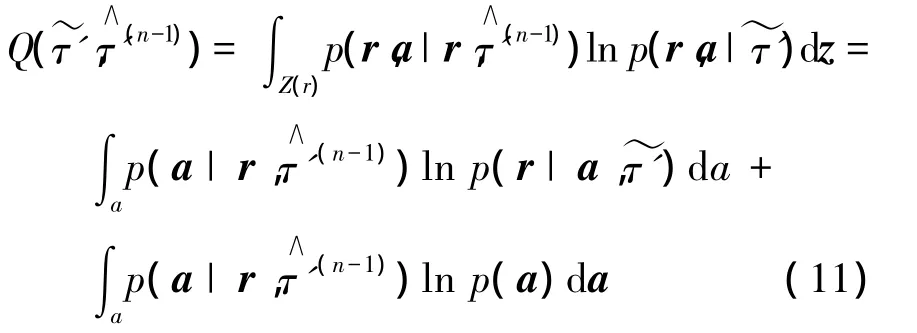
式(11)中的第二项与待估计参数无关，可以直接忽略，因此简化之后的Q函数为

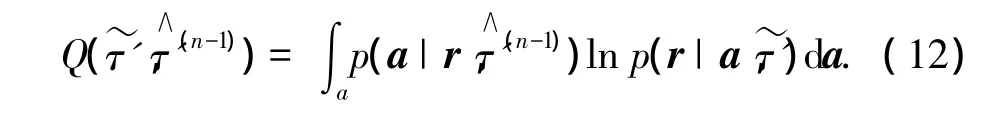
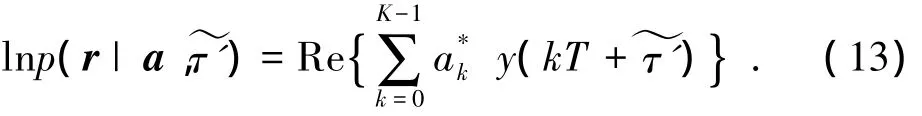
因此，Q函数的表达式为

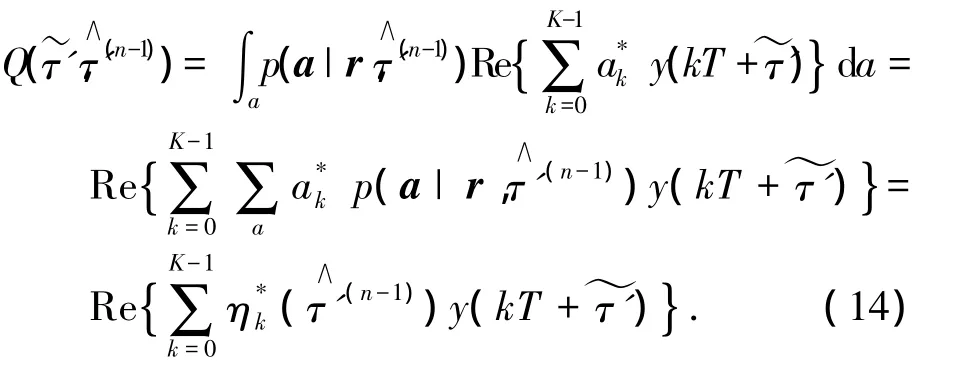
式中:

称为码元的后验均值，由高阶LDPC译码器输出.

依据EM算法原理，在获得Q函数之后，通过M步骤中的取最大值操作，即可获取定时偏移τ'的迭代估计值，为获得式(14)的最大值对应的定时偏移量，由牛顿 -拉普森算法可得

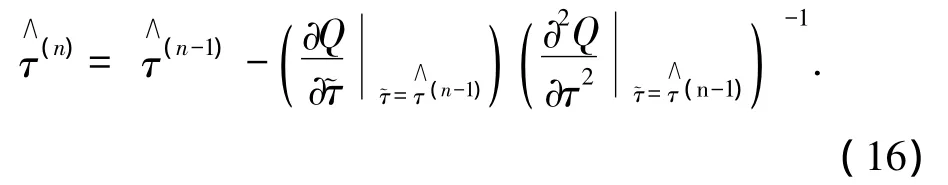
综上所述，可以获得基于最大似然准则的定时估计与高阶LDPC码的译码软信息之间的内在联系，使用式(14)和式(16)可以获得高阶LDPC码的定时细同步算法，该算法将解调器、译码器与定时同步器三者联合，以迭代的方式获得高可靠性的定时同步.

3 系统仿真与性能分析

使用提出的码辅助定时同步算法对高阶LDPC码的系统模型进行性能仿真与分析，各个仿真参数设置如下:采用1/2码率的16阶LDPC码，码长设为768 bit，校验矩阵构造方式为PEG方法［12］，定时同步器与译码器联合迭代的最大次数设为20次，归一化信噪比范围为0 dB≤Eb/N0≤5 dB，归一化定时偏移范围设定为［－1，+1］.为验证码辅助定时同步算法有效性，分别对同步精度和误码率性能进行数值仿真.

图4为高阶LDPC编码系统定时估计的均方误差曲线，图4同时给出了修正克拉美罗限(MCRB)［13］、理想 DA 估计、NDA 估计的性能曲线，其中，归一化定时偏移的MCRB的表达式为

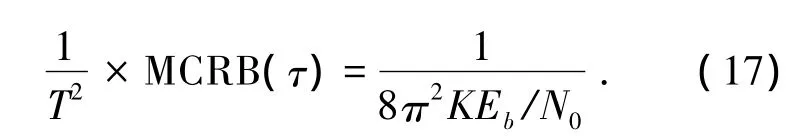
由图4可得:与理想的DA估计和NDA估计相比，本文所提的码辅助定时同步的估计性能介于两者之间;且当Eb/N0≥2 dB时，算法的估计误差逐渐接近MCRB，能够实现定时偏移的有效估计.

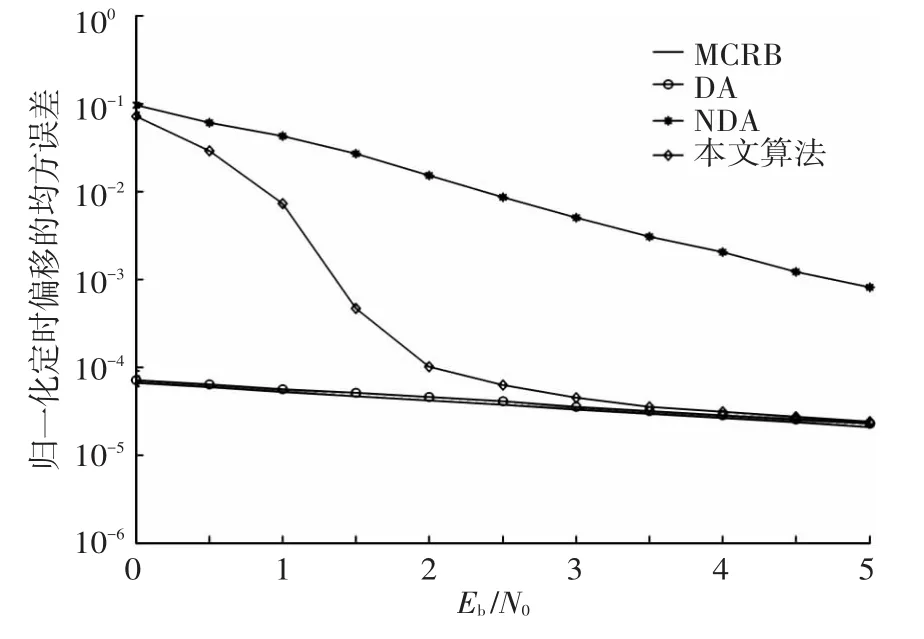
图4 定时估计的均方误差曲线

图5给出在2种定时偏移、不同信噪比条件下高阶LDPC编码系统的误码率性能，可见:当Eb/N0≥2 dB时，定时同步逐渐趋于收敛;与理想同步条件相比，系统的误码率性能损失低于0.2 dB，定时偏差对系统性能的影响得到抵消.

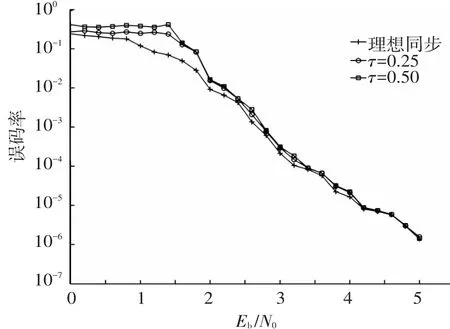
图5 高阶LDPC码的误码率性能曲线

图6给出在归一化信噪比分别为3 dB和5 dB条件下定时同步的有效范围，可以看到:提出的码辅助定时同步算法能有效估计的归一化定时偏移范围为|τ|＜0.75，同步范围较大.

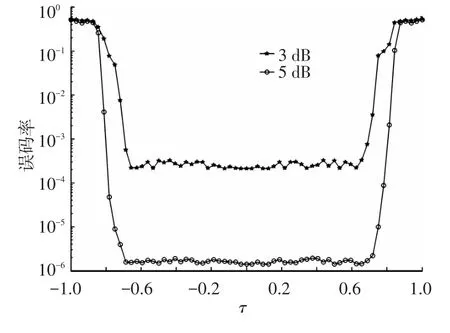
图6 定时同步有效范围

为显示所提码辅助定时同步算法的性能优势，分别从定时同步的范围、可有效同步的最低信噪比、系统误码率性能的损失3个方面将已有的定时同步算法与之对比，结果如表1所示.

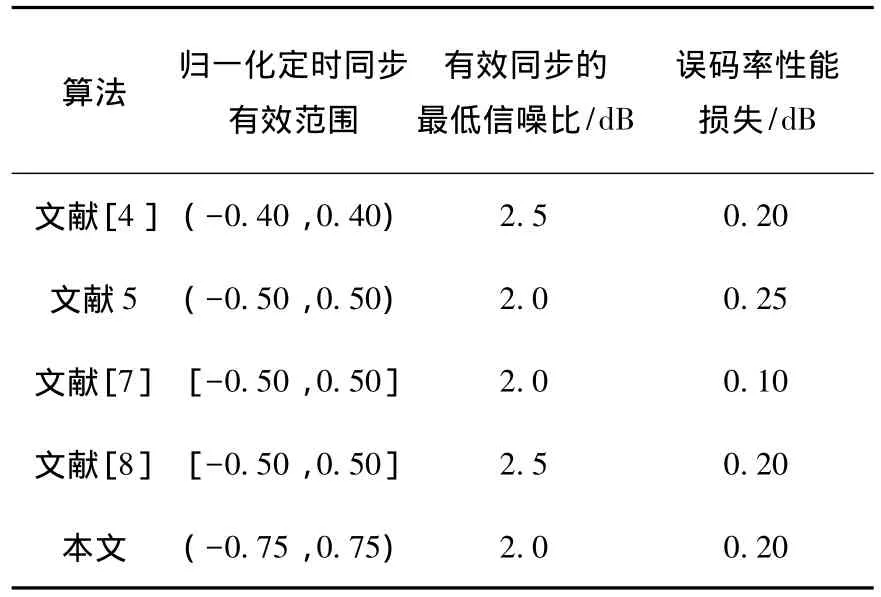
表1 定时同步的性能比较

从定时同步范围的角度，本文算法因同时采用定时粗同步和细同步，因此具有较大的同步范围，可达|τ|＜0.75，优于其他算法;从有效同步所需的最小信噪比来看，算法在2 dB以上即可实现高阶LDPC码的有效同步，具有在更低信噪比条件下有效同步的优点，同其他算法性能相当;另外，定时同步算法的误码率性能损失低于0.2 dB，性能较优.

在实现复杂度方面，定时粗同步在增大同步范围的同时增加了3次定时预补偿，与其他算法相比复杂度适量增加，但仍明显低于文献［6］中基于穷举搜索的M2S2O算法;定时细同步需要采用联合迭代的方式计算高阶LDPC码的软信息，运算复杂度与其他码辅助算法类似.在同步处理的延时方面，因定时细同步采用迭代的方式，与文献［4－8］算法相比，处理延时并无增加，而与传统的非迭代定时同步接收机相比，处理延时随迭代次数的增加而线性增加.

4 结语

深空通信具有传输距离远、接收信号微弱的缺点，在低信噪比的深空通信条件下，非理想的定时同步将使高阶LDPC码的性能严重恶化，本文提出的码辅助定时同步算法利用高阶LDPC译码软信息构造的代价函数进行定时粗同步，并使用基于最大似然准则的EM算法进行定时细同步，通过解调器、译码器与定时同步器的联合迭代来实现接近理想的定时同步.当Eb/N0≥2 dB时，系统的性能损失低于0.2 dB，定时同步的有效范围为|τ|＜0.75，所提算法的定时估计精度较高且同步范围较大，性能优良.

［1］GALLAGER R G.Low density parity check codes［J］.IRE Transactions on Information Technology，1962，8(3):208－220.

［2］ANDREWS K S，DIVSALAR D，DOLINAR S，et al.The development of turbo and LDPC codes for deepspace applications［J］.Proceedings of the IEEE，2007，95(11):2142－2156.

［3］NOZAKI T，KASAI K，SAKANIWA K.Analysis of error floors of generalized non-binary LDPC codes over q-ary memoryless symmetric channels ［C］//The IEEE International Symposium on Information Theory Proceedings.Cambridge MA:IEEE，2012:2341－2345.

［4］NOELS N，LOTTICI V，DEJONGHE A，et al.A theoretical framework for soft-information-based synchronization in iterative(Turbo)receivers ［J］.EURASIP Journal on Wireless Communications and Networking，2005，(2):117－129.

［5］薛英健，吴晓富，项海格.LDPC编码系统符号同步技术［J］.通信学报，2005，26(3):130－135.

［6］FREEDMANA， RAHAMINY， REICHMANA.Maximum-mean-square soft-output(M2S2O):a method for carrier synchronization of short burst Turbo coded signals［J］.IEEE Proc Communications，2006，153(2):245－255.

［7］BAO Jiaorong，ZHAN Yufen，LU Jinhai.Iterative timing recovery via soft decision metrics of low-density parity-check decoding ［J］. IET Communications，2010，4(14):1742－1751.

［8］MAN Xin，ZHAI Haitao，YANG Jun，et al.Improved code-aided symbol timing recovery with large estimation range for LDPC-Coded systems ［J］. IEEE Communications Letters，2013:1－4.

［9］史治平，唐发建，晏辉，等.极低信噪比下的导频联合编码辅助载波同步算法［J］.电子与信息学报，2011，33(10):2506－2510.

［10］DECLERCQ D，FOSSORIER M.Decoding algorithms for non-binary LDPC codesoverGF(q) ［J］.IEEE Transactions on Communications，2007，55(4):633－643.

［11］DEMPSTER A P，LAIRD N M，RUBIN D B.Maximum likelihood from incomplete data via the EM algorithm ［J］.Roy.Stat.Soc，1977，39(1):1－38.

［12］HU Xiaoyu，ELEFTHERION E.Progressive edge-growth Tanner graphs［C］//The IEEE GLOBECOM Global Telecommunications Conference.San Antonio TX:IEEE，2001:995－1001.

［13］ALDO N，ANDREA D，MENGALI U，et al.The modified Cramer-Rao bound and its application to synchronization problems ［J］.IEEE Transactions on Communications，1994，42(2):1391－1399.

Soft timing synchronization algorithm for LDPC codes on GF(q)in deep space communication

ZHOU Xiangchao，ZHAO Danfeng，XUE Rui
(College of Information and Communication Engineering，Harbin Engineering University，150001 Harbin，China)

Aiming at the timing synchronization difficulty of LDPC-coded system on GF(q)in deep space communication，a new soft timing synchronization algorithm is proposed.Firstly one cost function using the soft decoding information of LDPC on GF(q)is introduced for coarse timing synchronization，then the Expectation-Maximum algorithm is used for fine timing synchronization based on the maximum likelihood criterion.Conducting the joint iteration of timing synchronizer，demodulator and decoder，the soft information provided by LDPC decoder is used to aid the timing estimation，and the timing estimation close to the modified Cramer-Rao bound can be obtained by interpolation of the over-sampled data.Simulation results show that，at low SNRs，the efficient timing synchronization can be achieved with large timing offset，and almost ideal performance is obtained with low system complexity.

timing synchronization;LDPC codes on GF(q);code-aided;soft decoding information;deep space communication

TN919.3

A

0367－6234(2014)03－0110－05

2013－07－10.

武器装备预先研究项目(xxxx1200702)，中央高校基本科研业务专项基金资助项目(HEUCF130802).

周相超(1987—)，男，博士研究生;

赵旦峰(1961—)，男，教授，博士生导师.

周相超，shenzhou1987@126.com.

(编辑 苗秀芝)