掺杂硅硅栅晶圆片快速热处理工艺中的温度分布

王爱华，牛义红，刘 宇，陈铁军，李立亚

(1.东北大学材料与冶金学院，110819 沈阳;2.重庆大学动力工程学院，400030 重庆)

掺杂硅硅栅晶圆片快速热处理工艺中的温度分布

王爱华1，牛义红1，刘 宇1，陈铁军1，李立亚2

(1.东北大学材料与冶金学院，110819 沈阳;2.重庆大学动力工程学院，400030 重庆)

为了提高晶圆片温度分布的均匀性、改善加热元件性能，采用传导与辐射耦合传热模型，对快速热处理工艺中晶圆片内传热过程进行了数值模拟，研究了3种掺杂硅硅栅宽度(lG=40，50，60 μm)条件下，硅栅宽度与图案周期之比(lG/lP=0.05，0.10，0.25)变化对晶圆片温度分布的影响.结果表明:在相同掺杂硅硅栅宽度条件下，随着硅栅排列密度的增加，晶圆片总的温度水平下降，晶圆片表面温度温差变小，温度均匀性提高;在相同硅栅排列密度条件下，随着硅栅宽度的增加，晶圆片温度水平不断提高，而晶圆片表面温度温差几乎没有变化.这是因为晶圆片表面图案结构变化改变了表面吸收特性，调整了对入射辐射能量的吸收和分配，影响了晶圆片温度水平和温度均匀性.

图案晶圆片;快速热处理工艺;热辐射;温度分布;热传输特性

随着半导体器件尺寸的不断微缩和对工艺处理性能要求的日益苛刻，提高晶圆片在快速热处理工艺中的温度均匀性成为目前半导体工业亟待解决的主要问题之一.温度的非均匀性除了会造成所注入离子的非均匀激发，还会造成多余的热应力从而形成晶体缺陷、影响加热元件的性能［1－2］.晶圆片表面图案结构是影响晶圆片温度均匀性的重要因素之一，因为它改变了晶圆片表面辐射特性，从而影响了入射辐射能在晶圆片表面的吸收、传输和分配［3－5］.然而，目前关于晶圆片温度分布的研究工作还仅仅局限于大尺度晶圆片，对于具有微尺度表面图案的晶圆片涉及甚少［6－8］;再者，文献［9－11］仅考虑晶圆片内的导热和表面热辐射，尚未考虑硅晶圆片内容积辐射效应的影响.因此，目前关于微尺度表面图案结构变化对于晶圆片温度均匀性的影响以及入射辐射能在晶圆片内热传输机制尚未得到清晰理解.

文中选择一掺杂硅硅栅晶圆片来模拟快速热处理工艺中晶圆片的加热过程.在热传输模型中，能量守恒方程中同时考虑傅里叶导热方程和辐射传热方程.采用扩散近似模型来解决辐射传热方程，同时采用普兰克平均值法来处理材料的光学特性来协助模拟计算.

1 理论基础

1.1 数值模型

本文研究对象为置于平行入射辐射热流条件下的掺杂硅硅栅图案晶圆片，如图1所示.其中晶圆片下部硅衬底尺寸为4.8 mm×4.8 mm×8.0 mm，掺杂硅硅栅的高度dG为200 μm.入射的辐射热流是50 W/cm2.

图1 掺杂硅硅栅晶圆片示意

1.1.1 能量方程

能量方程为

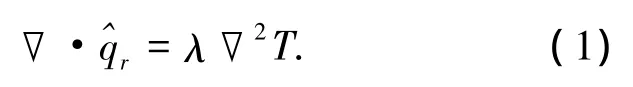
1.1.2 辐射传热方程

参与性介质中的辐射热传输可以用辐射传热方程来描述，由于散射效应在此忽略，因此方程变为

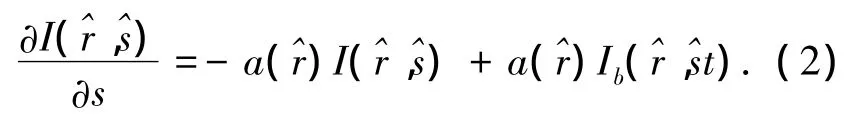
该方程可以通过多种方法来进行求解［12－13］.式(2)中采用扩散近似模型法.

1.1.3 球面谐波函数法

球面谐波函数法可以对辐射传输方程中扩散近似模型求解获得更高阶近似解.它假设辐射强度可以用正交Legendre多项式的序列求和来表示:

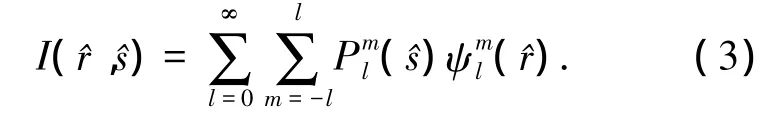
1.1.4 边界条件

顶部表面的边界条件为

式中:q0为垂直于顶部表面的平行入射辐射热流，50 W/cm2.发射率ε因材料的不同而不同.

底部表面和四周的边界条件为

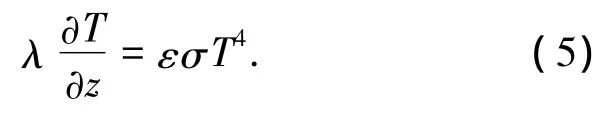
对于这些表面而言没有辐射.

1.2 热传输特性和光学特性选择

1.2.1 导热系数

傅里叶导热计算中的导热系数强烈依赖于温度和掺杂度.对于掺杂硅硅栅晶圆片，掺杂硅选取掺杂度为 7×1019cm－3.根据文献 ［10］，选用T=300 K时，得导热系数λu=160 W/(m·K)，λd=64 W/(m·K).

1.2.2 吸收系数

吸收系数对于晶圆片内入射能量的传播和吸收非常重要.对于非散射材料，随着光学厚度的增加，辐射衰减会变得更加明显.由于扩散近似模型不能进行光谱计算，所以采用普兰克平均特性近似计算以简化光谱效应.硅和掺杂硅的普兰克平均吸 收 系 数 分 别 为 aP，u=2 473.15 m－1和aP，d=112 341.36 m-1.

1.2.3 发射率

晶圆片表面发射率依赖于辐射光源的温度、辐射能的波长、发射角度以及表面图案特征.发射率是通过室温下波长的函数而计算获得［14］.由于扩散近似模型不能考虑发射率随波长的变化，所以实际计算中采用了普兰克平均发射率，硅发射率 εP，u=0.682，掺杂硅发射率 εP，d=0.688.

2 结果与讨论

2.1 晶圆片表面图案几何尺寸

表1给出了掺杂硅硅栅结构的几何尺寸.它用来探讨在3种固定的掺杂硅硅栅宽度lG条件下，硅栅宽度与图案周期之比(lG/lP)变化的影响结果.对于每一组尺寸，硅栅高度 dG设定为200 μm，掺杂硅硅栅宽度与图案周期之比(lG/lP)从5%逐步增加至25%，掺杂硅硅栅宽度从 40 μm 升至 60 μm.

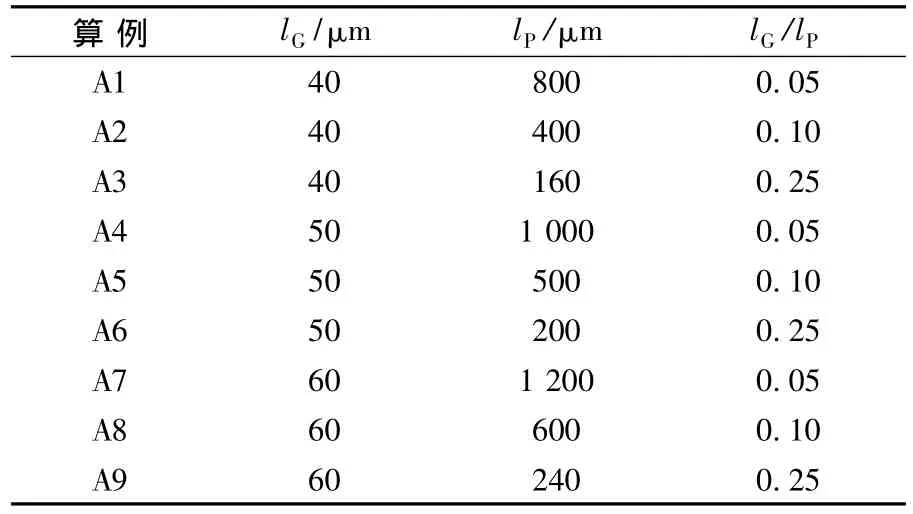
表1 掺杂硅硅栅结构的几何尺寸

2.2 掺杂硅硅栅排列密度对温度分布的影响

2.2.1 算例A1～A3分析

图2～4为掺杂硅硅栅宽度为40 μm条件下不同图案密度(0.05，0.10和0.25)晶圆片的温度分布.考虑到图形的对称性，这里截取1/2图进行分析.

图2 A1 算例(lG=40 μm，lG/lP=0.05)的温度分布

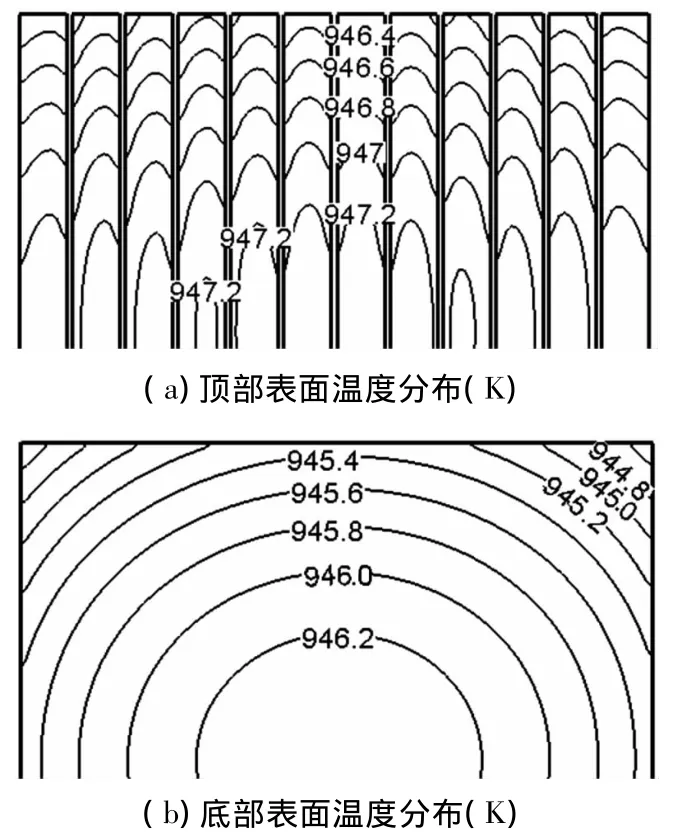
图3 A2 算例(lG=40 μm，lG/lP=0.10)的温度分布

对比图2～4可以看出，硅栅排列密度对晶圆片温度水平的影响十分明显.当硅栅排列密度lG/lP=0.05时，也就是排列最疏的时候，晶圆片的温度分布为980～984 K;当硅栅密度lG/lP=0.10时，晶圆片的温度分布为944～947 K;当硅栅密度为0.25时，晶圆片的温度分布为866～868 K.也就是说，随着晶圆片硅栅密度的增加，晶圆片总的温度水平在降低，从984 K降至866 K.

图4 A3 算例(lG=40 μm，lG/lP=0.25)的温度分布

就晶圆片顶部表面温差而言，不管硅栅密度如何变化，温差均为1.0 K;就晶圆片底部表面温差而言，当硅栅密度为0.05时，其温差为1.8 K;硅栅密度增加到0.10时，温差为1.4 K;硅栅密度为0.25时，温差为1.0 K.从等温线的疏密来看，随着硅栅密度的增加，晶圆片表面的等温线越来越稀疏，即温度均匀性越来越好.

2.2.2 算例A4～A6分析

图5～7为掺杂硅硅栅宽度为50 μm条件下不同图案密度(0.05，0.10和0.25)晶圆片的温度分布.

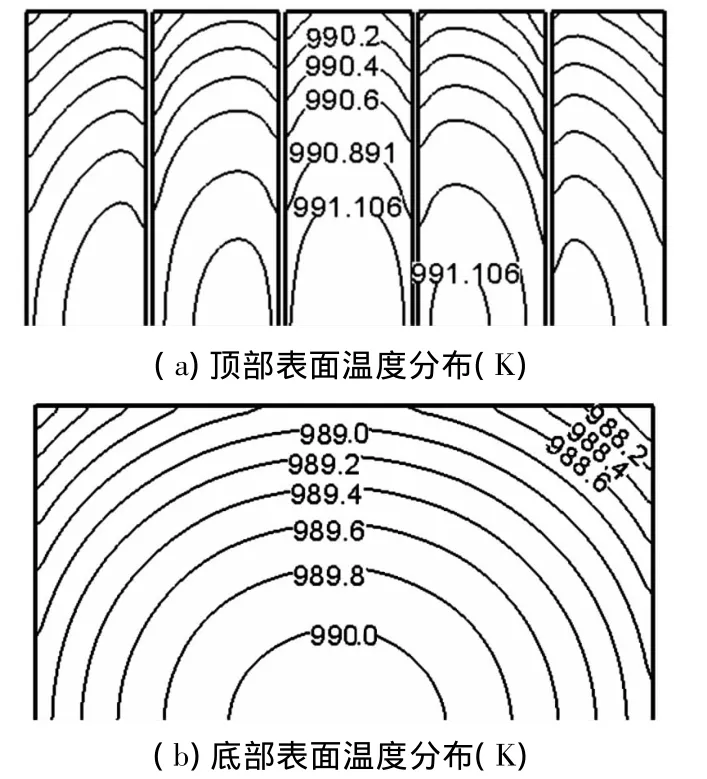
图5 A4 算例(lG=50 μm，lG/lP=0.05)的温度分布

图6 A5 算例(lG=50 μm，lG/lP=0.10)的温度分布

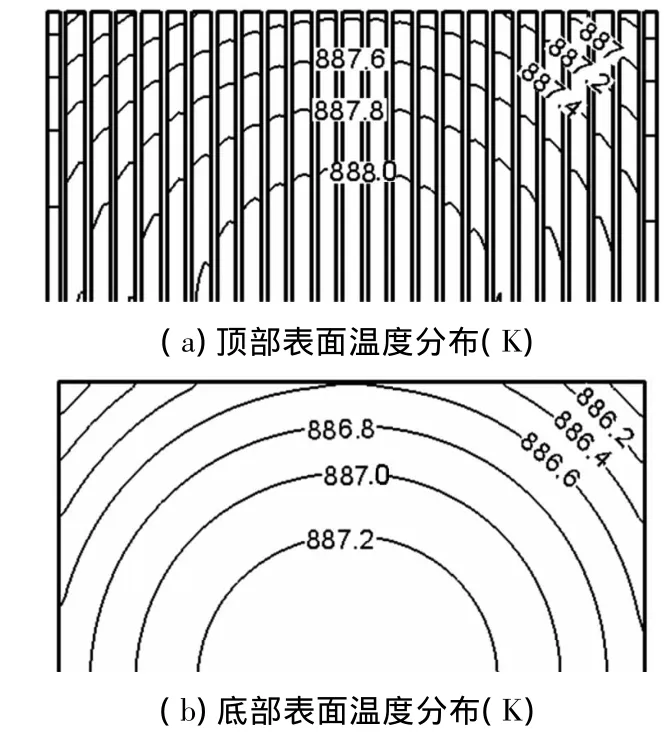
图7 A6 算例(lG=50 μm，lG/lP=0.25)的温度分布

对比图5～7可以看出，硅栅排列密度对晶圆片总的温度水平影响同样十分明显.当硅栅排列密度是0.05时，晶圆片的温度分布范围为988～991 K;硅栅密度是0.10时，晶圆片的温度分布为956～959 K;硅栅密度为0.25时，晶圆片的温度分布为886～888 K.也就是说，随着晶圆片上硅栅密度的增加，晶圆片的总的温度水平在降低.

从晶圆片顶部表面温度分布来看，3种硅栅密度条件下温差均为1.0 K;从底部表面温度分布来看，硅栅密度为0.05时，温差为1.8 K;硅栅密度为0.10时，温差为1.6 K;硅栅密度为0.25时，温差变为1.0 K.从晶圆片顶部和底部等温线的疏密情况即可看出，随着硅栅密度的增加，晶圆片表面的等温线越稀疏，温度均匀性越好.

2.2.3 算例A7～A9分析

图8～10为掺杂硅硅栅宽度为60 μm条件下不同图案密度(0.05，0.10和0.25)晶圆片的温度分布.

对比图8～10可以看出，硅栅排列密度对晶圆片温度水平影响同样十分明显.当硅栅排列密度是0.05时，也就是排列最疏的时候，晶圆片总的温度水平为994～997 K;硅栅密度是0.10时，晶圆片的温度水平为967～970 K;硅栅密度为0.25时，晶圆片的温度水平为904～907 K.也就是说，随着硅栅密度的增加，晶圆片的温度水平在降低，降低幅度约90 K.

图8 A7 算例(lG=60 μm，lG/lP=0.05)的温度分布

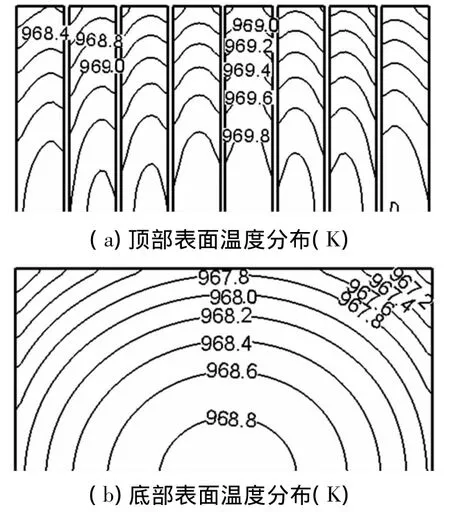
图9 A8 算例(lG=60 μm，lG/lP=0.10)的温度分布

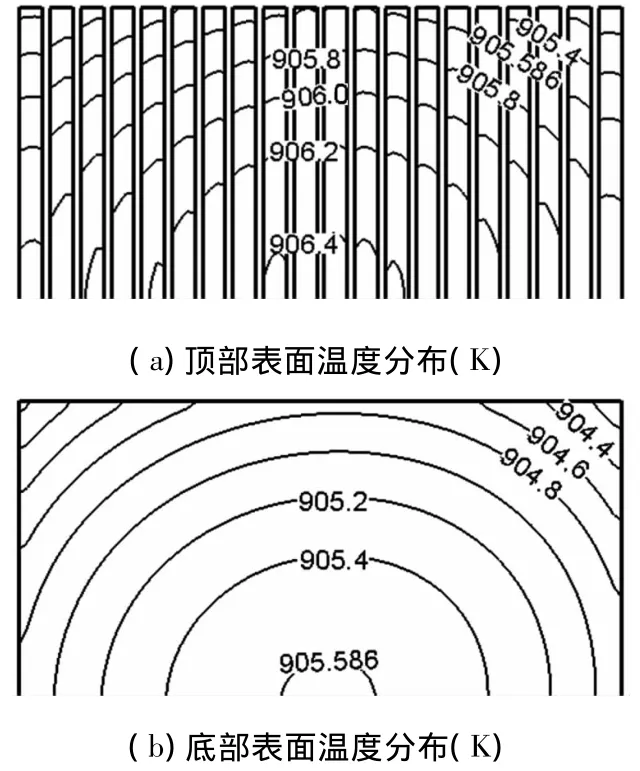
图10 A9 算例(lG=60 μm，lG/lP=0.25)的温度分布

就晶圆片顶部表面温度分布而言，当硅栅排列密度为0.05时，温差约为1.6 K;当硅栅密度为0.10时，其温差为1.4 K;当硅栅密度增加到0.25时，温差变为1.0 K.从晶圆片底部表面温度分布可以看出，当硅栅密度为0.05、0.10和0.25时，温差分别为1.8、1.6和1.2 K.因此，随着硅栅排列密度的增大，晶圆片表面温差越来越小，即温度均匀性越来越好，这一点可从等温线的疏密分布情况得以印证.

2.3 掺杂硅硅栅宽度对温度分布的影响

图2、图5和图8为硅栅排列密度相同(lG/lP=0.05)、硅栅宽度不同(lG=40，50，60 μm)条件下晶圆片(A1、A4和A7)温度分布情况.可以看出，随着硅栅宽度的增加，晶圆片温度水平不断提高，具体而言，晶圆片温度水平从 980～984 K增至988～991 K再增至994～997 K.对于硅栅排列密度lG/lP=0.10，对比图3、图6和图9可以看出，当硅栅宽度由40 μm增至50 μm再增至60 μm时，晶圆片温度水平从 944～947 K增至988～991 K再增至956～959 K.同样，对于硅栅排列密度 lG/lP=0.25而言，也表现出同样的变化规律.

以图2、图5和图8为例，就晶圆片表面温差而言，其顶部表面温差均为1.0 K，底部表面温差均为1.8 K;其余两种硅栅密度条件下也有同样的变化规律.因此，同等硅栅排列密度条件下，硅栅宽度的增加对于晶圆片表面温差几乎没有影响.

3 结论

1)在相同掺杂硅硅栅宽度条件下，随着硅栅排列密度的增加，晶圆片总的温度水平在下降，晶圆片表面温差越来越小，等温线越来越稀疏，即温度均匀性不断提高.

2)在相同硅栅排列密度条件下，随着硅栅宽度的增加，晶圆片总的温度水平不断提高，而晶圆片表面温差几乎没有变化，这说明硅栅宽度变化对于晶圆片温度均匀性影响甚微.

［1］FUKUDA H.Rapid Thermal Processing for Future Semiconductor Devices ［M］. San Diego:Elsevier，2003.

［2］JEFFREY M，JAMES W，DAVID M O，et al.Impact of pattern and LSA stitching effects and processing parameters on reflectance and stress distribution for thermal annealing technologies［C］//Proceedings of the 17th IEEE InternationalConference on Advanced Thermal Processing of Semiconductors.New York:IEEE，2009:1－6.

［3］TAKAGI R，LIU Kangzhi.Model-based control for rapid thermal processing of semiconductor wafers［J］.IEEE Transactions on Industry Applications，2011，131(2):159－165.

［4］REICHEL D，SKORUPA W，LERCH W，et al.Temperature measurement in rapid thermal processing with focus on the application to flash lamp annealing［J］.Critical Reviews in Solid State and Materials Sciences，2011，36(2):102－128.

［5］王爱华，蔡九菊.图案几何参数对硅晶圆片表面吸收率的影响［J］.东北大学学报(自然科学版)，2011，32(5):687－690.

［6］LORD H A.Thermal and stress analysis of semiconductor wafers in a rapid thermal processing oven［J］.IEEE Transactions on Semiconductor Manufacturing，1988，1(3):105－114.

［7］REICHEL D，SKORUPA W，LERCH W，et al.Temperature measurement in rapid thermal processing with focus on the application to flash lamp annealing［J］.Critical Reviews in Solid State and Materials Sciences，2011，36(2):102－128.

［8］RUDAKOV V I，OVCHAROV V V，PRIGARA V P.Influence of optical properties of the SOI structure on the wafer temperature during rapid thermal annealing［J］.Russian Microelectronics，2012，41(1):15－24.

［9］RUDAKOV V I，OVCHAROV V V，PRIGARA V P.Influence of a rough surface of the silicon wafer on its temperature during heating with incoherent radiation［J］.Mikroelektronika，2010，39(1):3－13.

［10］LOJEK B.Wafer temperature non-uniformity due to volumetric absorption of radiation［C］//Proceedings of the 12th IEEE International Conference on Advanced Thermal Processing of Semiconductors.Piscataway:IEEE，2004:203－206.

［11］OH H K，KANG S B，CHOI Y K，et al.Optimization of rapid thermal processing for uniform temperature distribution on wafer surface ［J］. Journal of Mechanical Science and Technology，2009，23(6):1544－1552.

［12］SIEGEL R，HOWELL，J R.Thermal Radiation Heat Transfer［M］.4th ed. New York:Taylor ＆Francis，2002.

［13］MODEST M F.Radiative Heat Transfer［M］.2nd ed.San Diego:Academic Press，2003.

［14］FU C J，ZHANG Z M.Nanoscale radiation heat transfer for silicon at different doping levels［J］.Journal of Heat and Mass Transfer，2006，49(9/10):1703－1718.

Temperature distribution of wafer with a doped silicon gate array during Rapid Thermal Process

WANG Aihua1，NIU Yihong1，LIU Yu1，CHEN Tiejun1，LI Liya2
(1.School of Materials and Metallurgy，Northeastern University，110819 Shenyang，China;2.College of Power Engineering，Chongqing University，400030 Chongqing，China)

To improve the temperature uniformity of the wafer and better the device performance，a combined conduction and radiation heat transfer model was used to simulate the heat transfer within wafer during Rapid Thermal Process，and the effects of the ratio of gate width to the pattern period(lG/lP=0.05，0.10，0.25)on the temperature distribution were investigated，under three fixed doped silicon gate widths(lT=40，50，60μm).The results show that，under the same doped silicon gate width，the temperature level of wafer decreases，the temperature difference reduces and the temperature uniformity of the wafer surface increases with the increase of the pattern arrangement density.Under the same doped silicon gate arrangement density，the temperature level enhances but the temperature uniformity changes little with the increase of the doped silicon gate width.This is because the wafer pattern structure changes the surface absorptance，adjusts the absorbing and distributing level of incident radiation energy，and transforms the temperature level and uniformity.

patterned wafer;Rapid Thermal Process;heat radiation;temperature distribution;heat transport properties

O551.2

A

0367－6234(2014)03－0124－05

2013－04－11.

中央高校基本科研业务费专项资金资助项目(N110204015);中国博士后科学基金面上资助项目(2012M510075).

王爱华(1976—)，男，博士，副教授.

王爱华，wangaihua1976@aliyun.com.

(编辑 张 红)