惯性矩二次变化变截面梁柱几何非线性分析

孟丽霞，陆念力，刘士明

(哈尔滨工业大学机电工程学院，150001 哈尔滨)

惯性矩二次变化变截面梁柱几何非线性分析

孟丽霞，陆念力，刘士明

(哈尔滨工业大学机电工程学院，150001 哈尔滨)

为研究考虑剪切变形的变截面梁杆结构几何非线性问题，应用Timoshenko梁理论，采用位移、转角独立插值的方法，获取考虑剪切影响的惯性矩二次变化变截面梁单元的形函数;从严格的虚功增量方程出发，建立同时考虑轴力、剪切、弯曲效应及其耦合项的平面变截面梁柱单元几何非线性增量平衡方程，得到惯性矩二次变化变截面梁单元大位移切线刚度阵;与经典算例进行对比，验证了本文方法的精确性与有效性.

有限单元法;变截面梁;虚功增量方程;大位移;几何非线性

梁杆结构由于自重轻、承载能力大等优点而在工程中得到广泛应用.随着优质钢材等级的提高，梁杆结构跨度与柔度不断增大，梁杆结构的受载形式表现为强非线性，此时传统的小位移假定已不再适用.在几何非线性分析方面，1975年，文献［1］提出了非线性增量形式的完全拉格朗日(T.L.)和修正拉格朗日(U.L.)描述.文献［2］改进了 Bathe的方法，通过建立三维连续梁的虚功增量方程，推导了分析三维梁式构件大挠度问题的U.L.列式法，并提出了新形式的梁单元之几何刚度阵.文献［3］通过建立考虑剪切变形与弯曲变形影响的修正剪切方程，对半刚性连接的单根梁柱的大位移大转动小应变问题进行分析研究.文献［4］使用C.R法分析了薄壁梁的大位移几何非线性问题.但上述研究对象均为等截面梁，对于变截面梁单元，文献［5］在获得小位移Euler-Bernoulli变截面梁单元刚度阵基础上，利用随动坐标法，在变形后位形上建立单元随动坐标系，得到变截面梁单元大位移全量平衡方程，所得刚度阵并未计及剪切变形的影响.文献［6］基于修正的拉格朗日列式法，采用等截面Timoshenko梁单元形函数代入虚功方程，给出了可直接用于几何非线性分析的变截面梁单元弹性和几何刚度矩阵.以往研究中，要么对变截面梁单元形函数简单采用等截面形函数代替［6］，并未考虑剪切变形与变截面因素的影响，要么在虚功方程中忽略了单元轴向变形与剪切变形及各耦合项对结构的影响［7～8］.

本文利用多项式插值，采取转角与位移独立插值的方法构造计及剪切与变截面因素的位移场，随后运用更新的拉格朗日列式法建立严格的平面梁柱单元的大位移虚功增量方程，得到包括各种耦合项的惯性矩二次变化变截面梁单元大位移切线刚度阵.最终得到显示表达的变截面梁单元大位移线性刚度阵与几何刚度阵.

1 惯性矩二次变化变截面梁单元

变截面梁单元以其受力合理以及节约材料等特点而得到广泛应用.工程中，等效为惯性矩二次变化的变截面梁多见于格构式结构与腹板镂空的工字梁.如图1所示惯性矩二次变化的变截面梁，构件截面面积为定值A0，构件长度为L，在x=0处的截面惯性矩为I1，在x=L处的截面惯性矩为I2，则任意截面x处的截面惯性矩可表示为坐标x的函数:

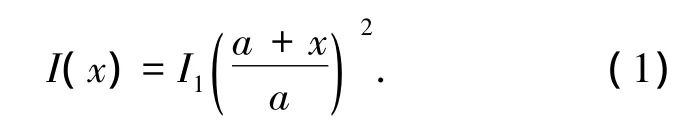
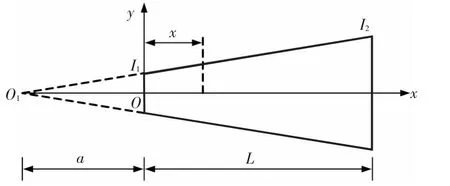
图1 平面变截面梁单元

在单元局部坐标系下，推导变截面梁单元切线刚度矩阵过程中使用如下基本假定:

1)梁单元变形后的截面形状保持不变，即为刚性截面;2)梁单元受载形式为大位移小应变情况;3)垂直于中面的截面变形后仍保持为平面，但不必再与变形后的中面垂直;4)单元材料为各向同性线弹性材料，遵循广义虎克定律;5)构件截面特性沿轴向连续变化，且构件为双轴对称.则构件的横截面面积及截面惯性矩可表示为轴向坐标的函数形式

2 变截面梁单元位移插值函数

在有限元分析中，需要先确定位移模式，本文对位移增量场采用多项式插值，即:对轴向位移增量采用线性函数插值，对横向位移增量采用三次函数插值，对转角位移增量采用二次函数插值.如图2所示，单元左右两端横向位移分别为yi、yj，相应的转角位移记为 θi、θj，单元长度为 L.则单元位移可表示为

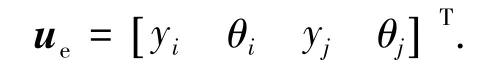
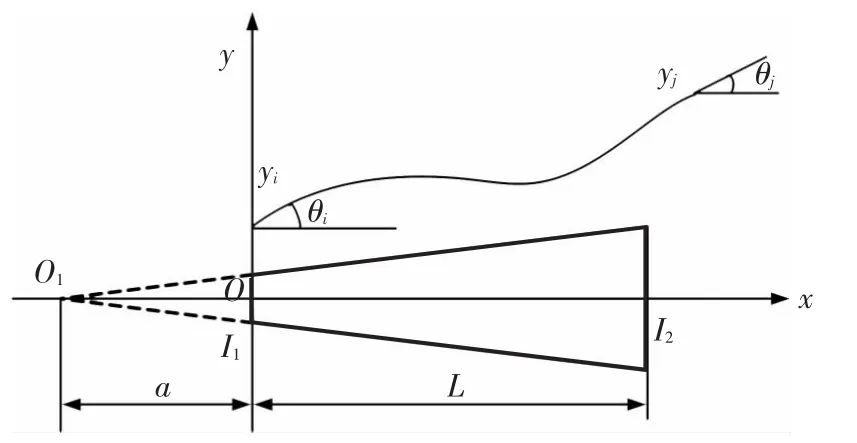
图2 变截面梁单元的位移描述

根据势能驻值原理，考虑剪切变形的单元总势能为

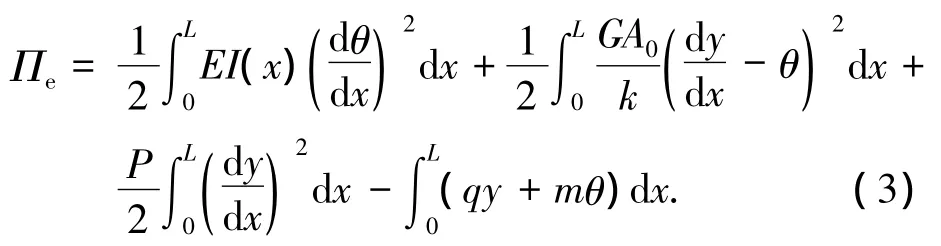
将式(3)列写为矩阵形式有

式中:Ke为单元线性刚度矩阵，Ge为单元几何刚度矩阵，Fe为广义载荷向量.

为了计入剪切变形影响，假设挠度函数ω(x)与转角函数ψ(x)分别表示为

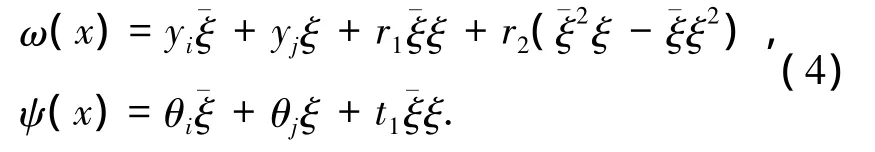
单元内部自由度r1、r2、t1的大小可由单元应变能确定，由式(3)可知，单元应变能表示为

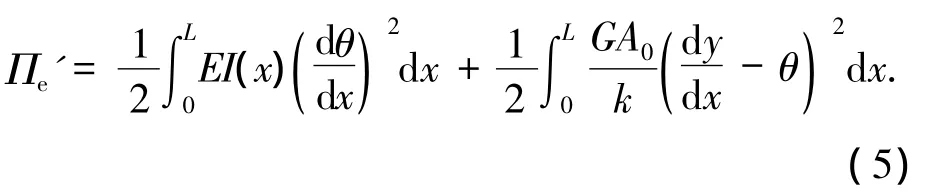
将式(4)代入式(5)，积分后化为矩阵形式:

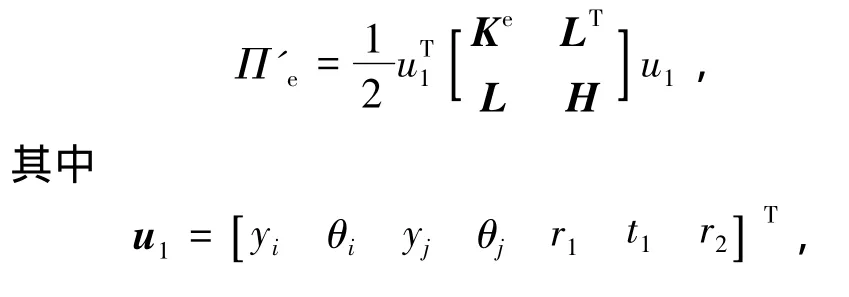
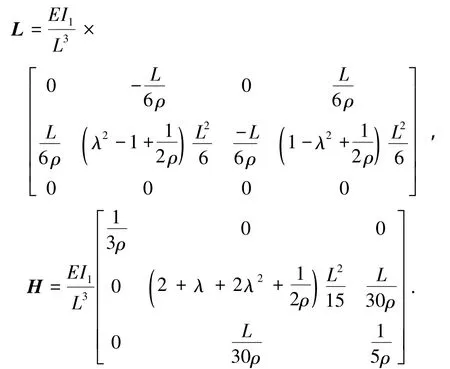
式中:ρ为量纲一的剪切系数，ρ=EI1k/(GAL2);λ为锥度系数L)/a;k为截面剪切校正因子.

系数 r1、r2、t1应使应变能 Πe'取最小值，故

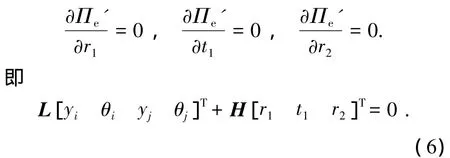
由式(6)，利用静力凝聚，将 r1、r2、t1用 yi、θi、yj、θj表示，得到已消除内部自由度的横向位移与转角

不难证明，当变截面锥度系数λ→1时，本文梁单元横向位移与转角表达式(7)、(8)将相应发生退化，退化后的表达式与文献［9］中考虑剪切变形的等截面梁单元相同.

3 几何非线性有限元增量平衡方程

采用U.L.列式法来建立梁柱单元的几何非线性增量刚度方程.根据有限元理论，以t时刻位形为参考位形，建立梁单元U.L.格式下的虚功增量方程:

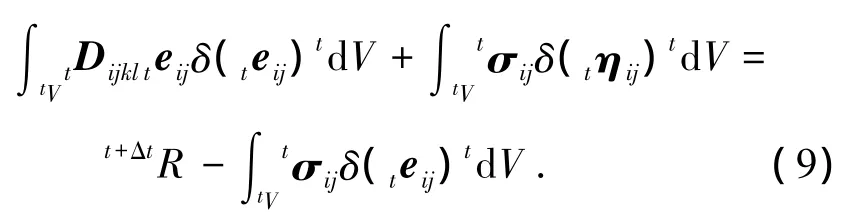
式中:Dijkl为单元本构关系矩阵;eij为格林应变张量线性项;ηij为格林应变张量非线性项;σij为单元柯西应力;t+ΔtR为t+Δt时刻外力所做的虚功.

本构关系矩阵为

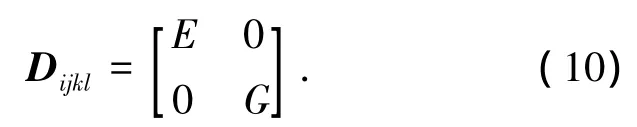
式中:E为弹性模量，G为剪切模量.

因为已知方程中所有的物理量都是以t时刻为基准来度量的，而t时刻为已知状态，因此，在以下分析中省去左上角标及左下角标t.

将式(10)带入式(9)，并考虑应变分量与应变张量表达之间的关系，可得相应的虚功增量方程为

式中格林应变张量的线性项与非线性项表达如下:

式中:“，”表示对后面坐标的导数，Ux0，Uy0为截面x形心处的位移增量，θ为截面x的转动增量.

变截面梁单元任意截面x处的位移增量可表示为

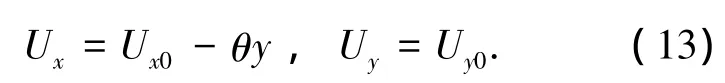
结合式(2)、(11)～(13)有如下关系式:

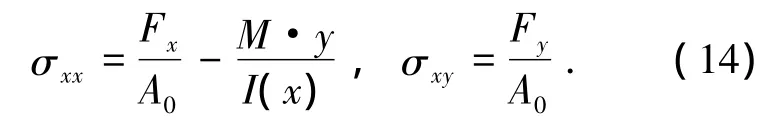
可得平面梁柱单元的虚功增量方程

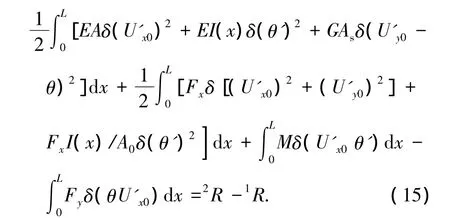
式中:As为单元抗剪切面积，As=A0/k;2R为t+Δt时刻外力所做虚功，即2R=t+ΔtR;1R为t时刻外力所做虚功，即

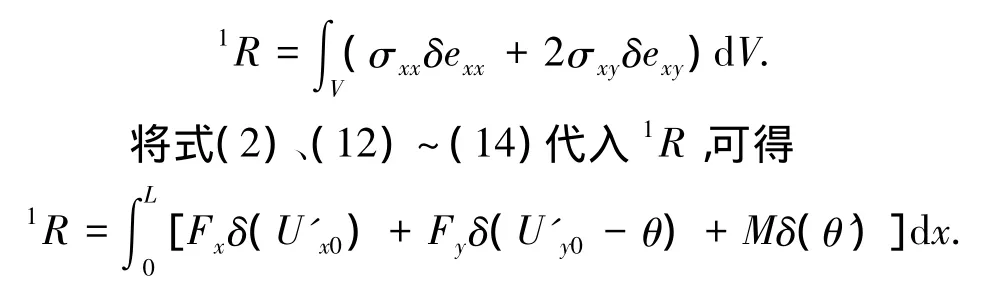
方程(15)即为平面梁柱单元的虚功增量方程，式中包括了轴向变形、剪切变形、弯曲变形以及它们之间的耦合项.

4 变截面梁单元之大位移刚度阵

平面变截面梁单元杆端力与杆端位移如图3所示.

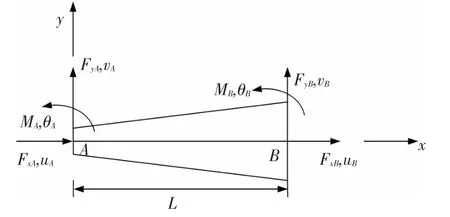
图3 平面梁柱单元杆端力与杆端位移

单元节点位移向量

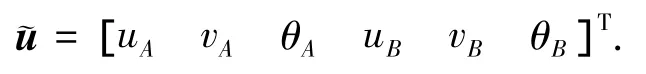
单元节点载荷向量

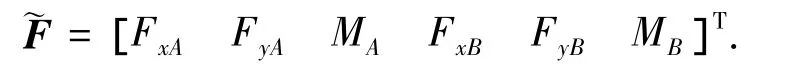
轴向位移选用线性函数插值，横向位移与转角采用式(7)、(8)考虑剪切变形的三次多项式插值.则单元任意截面质心处位移增量与杆端位移增量间的关系为

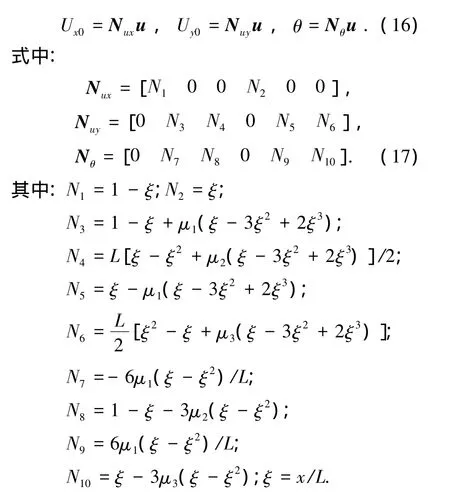
将单元截面内力用其杆端力表示为

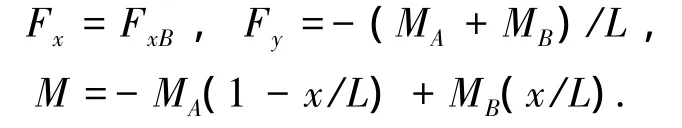
将式(1)、(16)、(17)代入单元虚功增量方程(15)，可得三维梁柱单元的几何非线性刚度方程

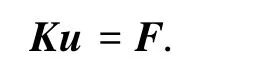
式中K即为惯性矩二次变化变截面梁柱单元的大位移切线刚度矩阵，其表达式为

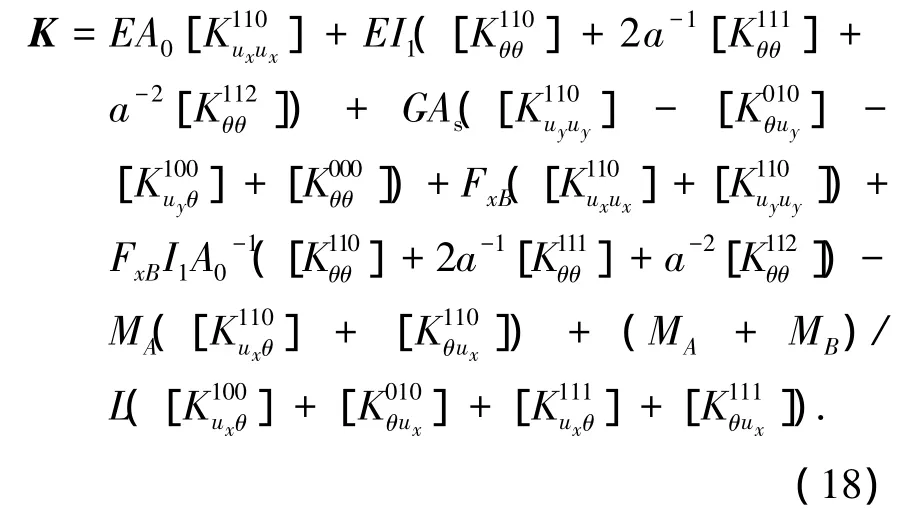
式中:

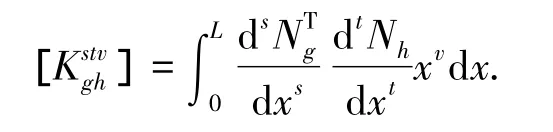
其中:下标g和h表示位移ux、uy或θ，上标s和t表示对位移插值函数N求导的阶数，v则表示以x为底的幂函数的次数.

将式(17)带入式(18)，可得变截面梁单元大位移刚度矩阵

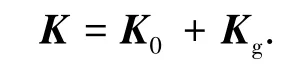
式中:K0为变截面梁单元之弹性刚度矩阵，Kg为变截面梁单元之几何刚度矩阵.

线性刚度阵表达式为

几何刚度阵表达式为

5 算例

算例1 如图4所示典型的Williams曲肘，两杆均为等截面直杆，两端约束方式为固接，在曲肘顶点处施加竖向载荷 P.结构参数 L=657.5 mm，h=9.8 mm，a=19.126 mm，b=6.172 mm，弹性模量取E=71 GPa.计算在承受轴力P作用时顶点处的竖向位移δ，使用本文方法对该结构进行大位移非线性分析，每根杆件划分为20个单元，计算所得结果与文献［10］中Williams解析解进行比较，如图5所示.

图4 等截面Williams曲肘模型

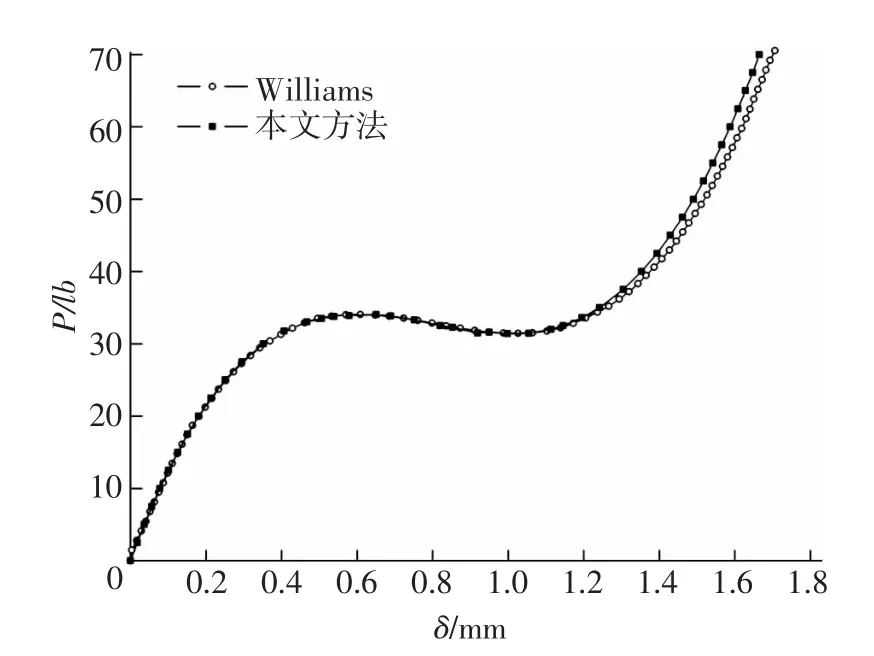
图5 Willams曲肘轴向载荷位移曲线

由图5可见，两种方法所得结果吻合较好，证明了本文方法的有效性，本文推导的变截面梁单元退化得到的等截面梁单元在大位移非线性分析时，保持了较高的计算分析精度.

算例2 如图6所示变截面悬臂梁，自由端承受横向集中力Q作用.取构件小端截面面积A0=0.04 m2，小端截面惯性矩 I0=1.33×10－4m4，大端截面惯性矩为2I0，构件长度L=1.0 m，弹性模量E=200 GPa，剪切模量G=71 GPa，采用量纲一载荷κ=QL2/EI0，取截面剪切校正因子k=10/9，(x，y)表示梁杆轴线上任意点坐标值.本文将构件离散为20个单元进行计算，所得结果与ANSYS将构件划分为20个单元的结果进行对比如表1所示.

图6 变截面悬臂梁模型

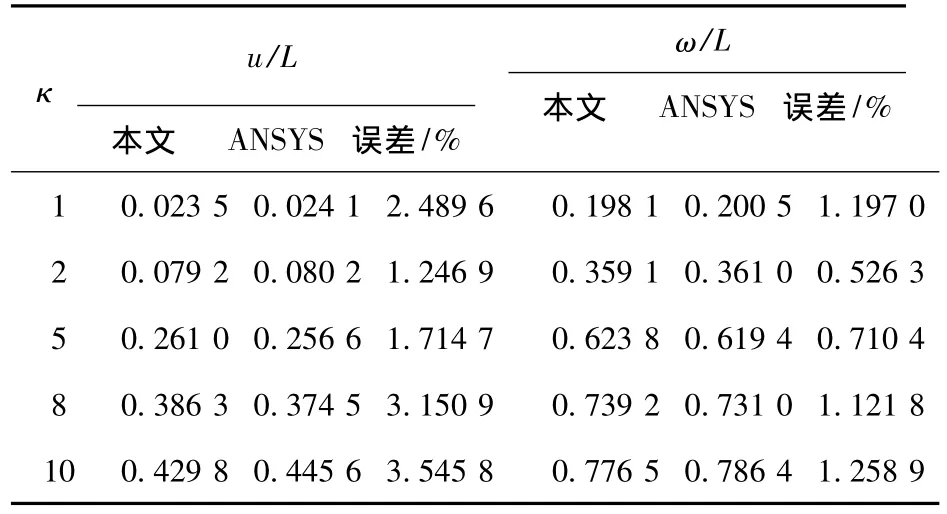
表1 本文方法与ANSYS大位移分析结果比较

图7给出了κ=1、2、5、8、10时该悬臂梁大位移变形后的构型.图中横纵坐标分别为构件轴向坐标x、横向坐标y与构件总长L的无量纲比值.

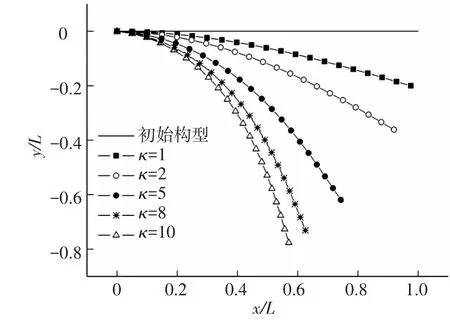
图7 变截面悬臂梁大位移构型

在大位移情况下，构件自由端横向位移随剪切系数变化情况如图8所示.可见，在相同载荷下，剪切刚度越弱，构件横向位移越大，剪切刚度对惯性矩二次变化变截面构件几何非线性影响较为显著.

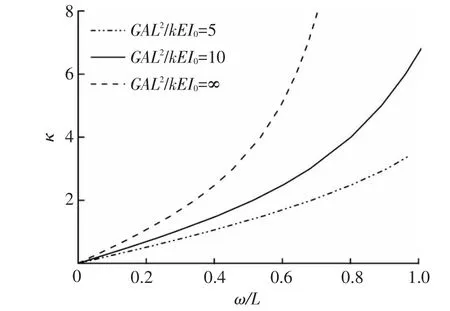
图8 不同剪切系数下的横向位移变化曲线

6 结论

1)利用多项式插值函数构造了计及剪切与变截面因素影响的位移场，采用U.L.列式法建立梁柱单元的几何非线性虚功增量方程，得到同时考虑轴力、剪切、弯曲效应及其耦合项的惯性矩二次变化变截面梁单元大位移切线刚度阵.

2)本文方法严格计入了剪切变形与变截面因素的影响，具有较高的计算精度，适用于变截面梁、等截面梁以及组合式梁杆结构的大位移几何非线性分析.

［1］BATHE K J.Finiteelementprocedures ［M］.Englewood Cliffs:Prentice Hall，1996:561－566.

［2］陈政清，增庆元，颜全胜.空间杆系结构大挠度问题内力分析的UL列式法［J］.土木工程学报，1992，25(5):34－44.

［3］ARISTIZABAL-OCHOA J D.Large deflection and postbuckling behavior of Timoshenko beam-columns with semirigid connections including shear and axial effects［J］.Journal of Engineering Structures，2007，29(6):991－1003.

［4］CHEN H H，LIN W Y，HSIAO K M.Co-rotational finite element formulation for thin-walled beams with generic open section ［J］.ComputerMethodsin Applied Mechanics and Engineering， 2006， 195(19):2334－2370.

［5］张宏生.杆系结构几何非线性动静态分析方法及其在塔机中的应用［D］.哈尔滨:哈尔滨工业大学，2009.

［6］郭彦林，王文明，石永久.变截面门式刚架结构的非线性性能［J］.工程力学，2000，17(4):29－36.

［7］LIEW J Y R，CHEN H，SHANMUGAM N E，et al.Improved nonlinear plastic hinge analysis of space frame structures［J］.Engineering Structures，2000，22(10):1324－1338.

［8］REMKE J，ROTHERT H.Eine geometrisch nichtlineare finite-element berechnung raumlicherstabtragwerke mittels einer Abspaltung von starrkorperbewegungen［J］.Bauingenieur，1999，74:139－147.

［9］王勖成.有限单元法［M］.北京:清华大学出版社，1997:278－292.

［10］WILLAMS F W.An approach to the non-linear behavior of the members of a rigid jointed plane framework with finite deflections［J］.Quarterly Journal of Mechanics and Applied Mathematics，1964，17(4):451－469.

Geometric nonlinear analysis of tapered beam with inertia moment vary quadratic

MENG Lixia，LU Nianli，LIU Shiming
(School of Mechatronics Engineering，Harbin Institute of Technology，150001 Harbin，China)

To research the geometric nonlinear problem of tapered beam with shear deformation，based on Timoshenko theory，the displacement and rotation independent interpolation method was adopted to obtain the shape functions of tapered beam considering shear deformation，whose inertia moment varied quadratic.Then，started from the virtual work increment equation，the geometric nonlinear incremental equilibrium equation of the plane tapered beam element was established，including axial force，shear effect，bending effect and its coupling term，and the large displacement tangential stiffness matrix of the tapered beam was obtained.Finally，the classical examples are calculated，and the results show that the proposed method is accurate and effective.

finite element method;tapered beam;virtual work increment equation;large displacement;geometric nonlinear

TU311.2

A

0367－6234(2014)03－0020－06

2013－03－29

国家科技支撑计划资助项目(2011BAJ02B01－02).

孟丽霞(1983—)，女，博士研究生;

陆念力(1955—)，男，教授，博士生导师.

孟丽霞，Menglixia1983@163.com.

(编辑 杨 波)