旋转矩形静矩与惯性矩关系系数研究

焦锡华,陆文林,庄　甜,俞晓明

(1.盐城工学院 机械优集学院,江苏 盐城　224051; 2.盐城工学院 基础教学部,江苏 盐城　224051)

旋转矩形静矩与惯性矩关系系数研究

焦锡华1,陆文林2,庄甜1,俞晓明2

(1.盐城工学院 机械优集学院,江苏 盐城224051; 2.盐城工学院 基础教学部,江苏 盐城224051)

静矩;惯性矩;关系系数;旋转矩形;正方形

构件的静矩与惯性矩取决于构件本身并决定了构件的性能，一般构件的静矩与惯性矩之间并没有简单的关系。研究液体的稳定度时，发现液体的稳定度取决于一个无量纲系数，这就是静矩与惯性矩关系系数[1]，该系数可将立体问题转化为平面问题。在材料力学中，研究的杆件其横截面大多是各种形式的平面图形(如矩形、圆形、T形、工字形等)，研究这些图形的几何性质时，恰恰都可以不考虑研究对象的物理和力学因素，而作为纯几何问题加以处理[2]。从理论上研究静矩与惯性矩关系系数对解决体系的平衡问题具有重要作用。本文研究的矩形绕其端点在其所在平面内旋转时静矩与惯性矩关系系数及其所具有的性质，对深刻理解和丰富发展静矩与惯性矩关系系数具有重要意义。

1　静矩与惯性矩关系系数的定义

如图1所示，平面图形K处于xoy平面内，在图形K上(x,y)处取面积微元dA，则平面图形K绕y轴的静矩Sy、惯性矩Jy以及绕x轴的静矩Sx、惯性矩Jx分别为

(1)

(2)

(3)

(4)

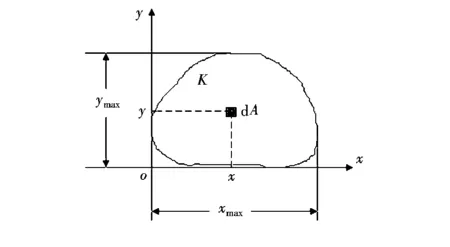
图1　静矩与惯性矩关系系数的定义Fig.1　Definition of the relational coefficient between static moment and moment of inertia

定义平面图形K绕y轴、x轴的静矩与惯性矩关系系数分别为

(5)

(6)

式(5)中的xmax和式(6)中的ymax分别为平面图形K在x轴和y轴方向上的最大长度。

2　旋转矩形静矩与惯性矩关系系数

2.1理论推导

如图2a，设边长分别为a、b的矩形ABCD处于坐标系xoy。将矩形及坐标系xoy绕原点O沿顺时针方向旋转θ(逆时针取正，顺时针取负)，得矩形A′B′C′D′,如图2b所示。

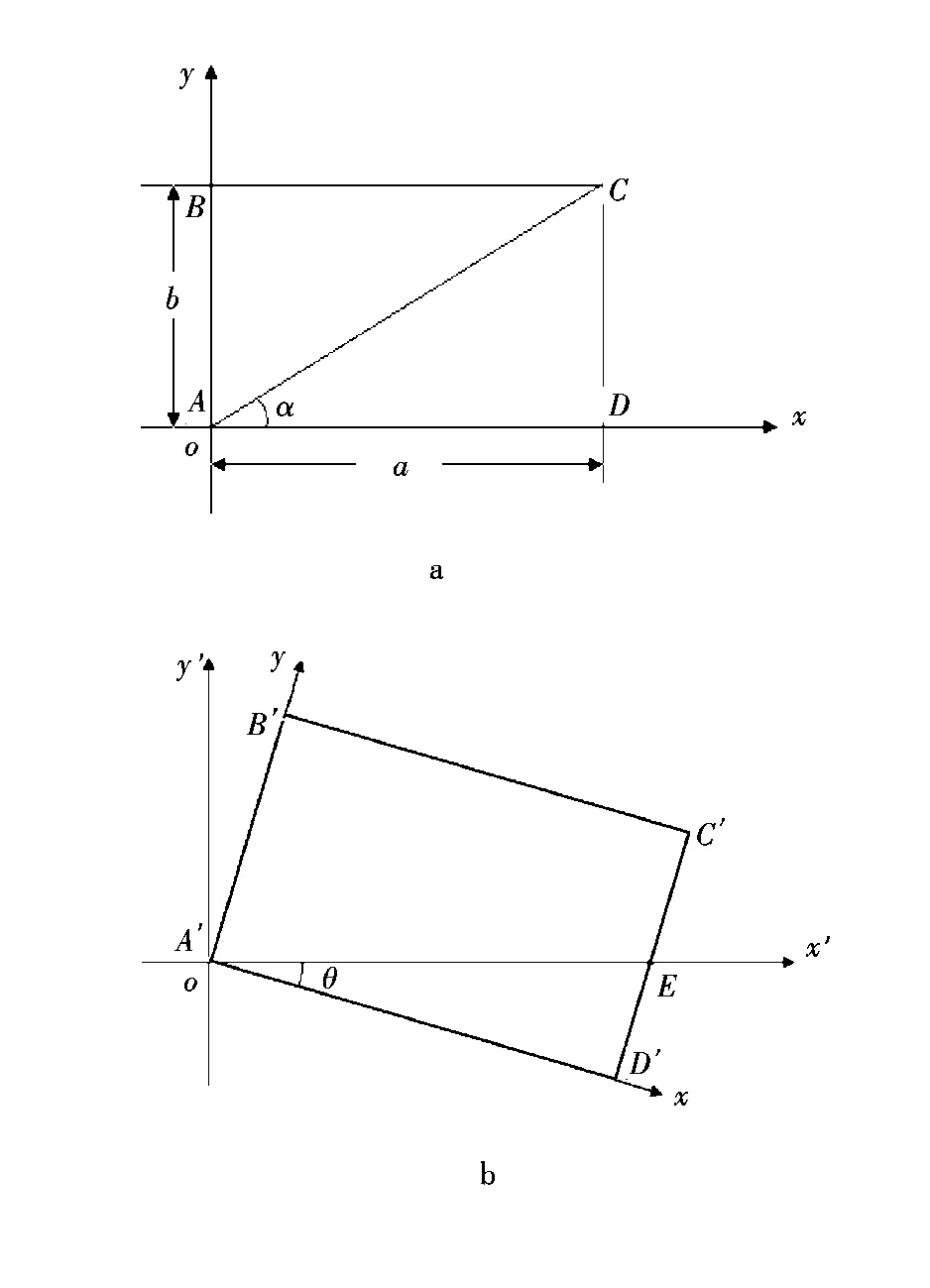
图2　矩形旋转Fig.2　Rotation of a rectangle

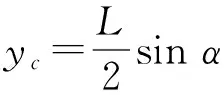
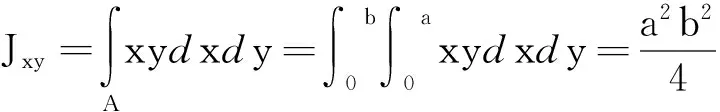
如图2b,矩形A′B′C′D′的质心横坐标分别为

(7a)

(7b)

矩形A′B′C′D′的绕轴x、y的静矩分别为

(8a)

(8b)

根据惯性矩的转轴公式[3]得

(9a)

(9b)

(10a)

(10 b)

(11a)

(11b)

式(8a)、(8b)、(9a)、(9b)、(11a)、(11b)表明：尽管矩形绕其顶点在其所在平面内旋转时，其静矩、惯性矩都在变化，但给定矩形的长宽比k以及旋转角θ，静矩与惯性矩关系系数py、px仍具有标度变换不变性。

2.2作图分析

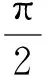
图3　k=1/4,1/3,1/2,1,2,3,4时，旋转矩形静矩与惯性矩关系系数的定义Fig.

2.3公式讨论

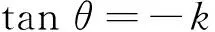
(12a)

(12b)

(13a)

(13b)

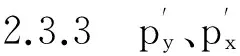
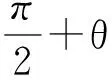
(14)

3　旋转正方形静矩与惯性矩关系系数

(15a)

(15b)

从图4可看出：

(3)图4是图3(a)、(b)中，k=1时的两种特殊情形。

图4　旋转正方形静矩与惯性矩关系系数py(θ)、px(θ)图Fig.4　Relational coefficient of a rotational square x(θ)

4　结束语

[1] 俞晓明.平面对称图形静矩与惯性矩的关系研究[J].盐城工学院学报:自然科学版,2013,26(1):5-9.

[2] 周金枝,姜久红.材料力学[M].武汉：武汉理工大学出版社,2013:228.

[3] 孙训方,方孝淑,关来泰.材料力学(Ⅰ)[M].北京:高等教育出版社,2002:330.

(责任编辑：张英健)

ResearchontheRelationalCoefficientofStaticMomentandMomentofInertiaofaRotatingRectangular

JIAOXihua1,LUWenlin2,ZHUANGTian1,YUXiaoming2

1． School of Mechanical Optimal Sets Yancheng Institute of Technology，Yancheng Jiangsu 224051，China，2． Department of Basic Courses，Yancheng Institute of Technology，Yancheng Jiangsu 224051，China

staticmoment;momentofinertia;relationalcoefficientofstaticmomentandmomentofinertia;rotatingrectangular;square

10.16018/j.cnki.cn32-1650/n.201503004

2015-03-10

焦锡华(1995-),男,江苏常州人,主要研究方向为机械设计与自动化。

O312.3

A

1671-5322(2015)03-0017-04