基于梯度优化法的基坑整体稳定可靠度及模糊可靠度分析

朱海陶,廖　瑛,黄　斌,3,郭宇飞,黄　波

1． 苏州科技学院土木工程学院，江苏苏州215011;2． 同济大学航空航天与力学学院，上海200092;3． 同济大学土木工程学院，上海200092

基于梯度优化法的基坑整体稳定可靠度及模糊可靠度分析

朱海陶1,2,廖瑛1,黄斌1,3,郭宇飞1,黄波1

1． 苏州科技学院土木工程学院，江苏苏州215011;2． 同济大学航空航天与力学学院，上海200092;3． 同济大学土木工程学院，上海200092

作为一类重要的基坑支护结构，重力式挡土墙整体稳定性研究一直备受众多学者极大的关注。从可靠度的几何意义出发，通过MATLAB编写程序，对最危险滑弧面所对应圆心进行全域搜索，并利用梯度优化法计算整体稳定可靠度，提高了整体稳定可靠度的计算精度。同时，计算了其模糊可靠度，对比计算结果可知，模糊可靠度理论能更加科学、全面、客观地反映复杂的岩土工程可靠度问题的实质。

梯度优化法;MATLAB;全域搜索;稳定可靠度;模糊可靠度

重力式挡土墙的整体失稳[1]是其主要的失稳形式之一，其整体稳定性分析具有保证基坑稳定的重要意义。目前，该领域的研究方法展现出以可靠度理论为基础的极限状态设计法的趋势。但是，基于结构可靠度理论的基坑支护结构稳定性问题的研究，其对应的某种失稳形式的功能函数往往是高度非线性函数，根据验算点法等计算可靠度需要将功能函数在验算点处线性化，这不仅会降低计算精度还可能导致收敛速度减缓乃至不收敛，故而由可靠指标的几何意义出发，采用优化算法解决这一问题是行之有效的途径。此外，由于岩土工程问题的复杂性，基坑整体稳定性问题除了具有随机性特点以外，往往还具有模糊性特点，故而采用模糊可靠度理论同时考虑问题的随机性和模糊性特点更为科学全面[2]。

针对基坑的整体稳定性研究，常用方法有瑞典圆弧法、简单条分法等。本文以简单条分法为例，利用梯度优化法和MATLAB编写相应分析程序，并利用模糊可靠度理论对某重力式挡土墙进行整体稳定性分析。

1　基坑整体稳定可靠度分析

1.1整体稳定性功能函数的建立

基坑整体稳定性计算方法，采用圆弧滑动面简单条分法，按总应力法取单位墙宽，可得整体稳定安全系数为[3]：

(1)

式中，cj、φj分别为第j土条滑弧面处土的粘聚力和内摩擦角；bj、lj分别为第j土条的宽度和底面面积；qj为作用在第j土条上附加均布载荷标准值；△Gj为第j土条的自重，按天然重度计算；θj为第j土条对应滑弧中点处法线与竖直线所成夹角。

则按照可靠度理论，当假设地下水位位于墙体以下时，可设整体稳定性的功能函数为：

(2)

1.2最危险滑弧面及圆心的确定

根据大量工程经验和研究已知，若以桩顶中心为原点建立笛卡尔坐标系并将其划分为A、B、C、D4个区域，则最危险的滑弧通过桩最底端c点且其对应圆的圆心在如图1所示的D区域[4]。故可对该区域利用MATLAB编程进行全域搜索，寻找最危险的滑弧面和圆心。

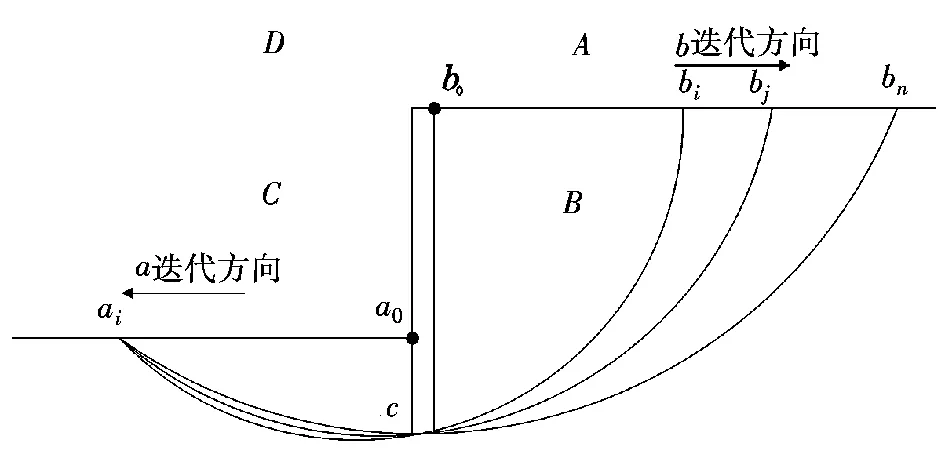
图1　全域搜索示意图Fig.1　Sketch map of global search

假定桩最底端为c点，滑弧左端a的初始搜索点为a0，滑弧右端b的初始搜索点为b0，则搜索步骤为：

①假定初始时a、b点均在桩的边界a0、b0处，且a、b的迭代步长为0.5 m;

②假设滑弧端a、b各自搜索的总长度按工程研究经验[5]取约为4.5倍的基坑深度；a每迭代一次，b就相应地从0～4.5H的范围内迭代搜索，即若a向左迭代m次，b向右迭代n次，则共迭代m×n次。滑弧b端每迭代一次就判断圆心位置，并对圆心位置在D区域的滑弧利用简单条分法和梯度优化法求解相对应的可靠度；

③对D区域圆心对应的可靠度集进行比较，求最小可靠度。则此最小可靠度值所对应的圆弧即为最危险圆弧，并求出相应失效概率即可。

按上述①、②步骤利用MATLAB求解可靠度集的流程如图2所示。

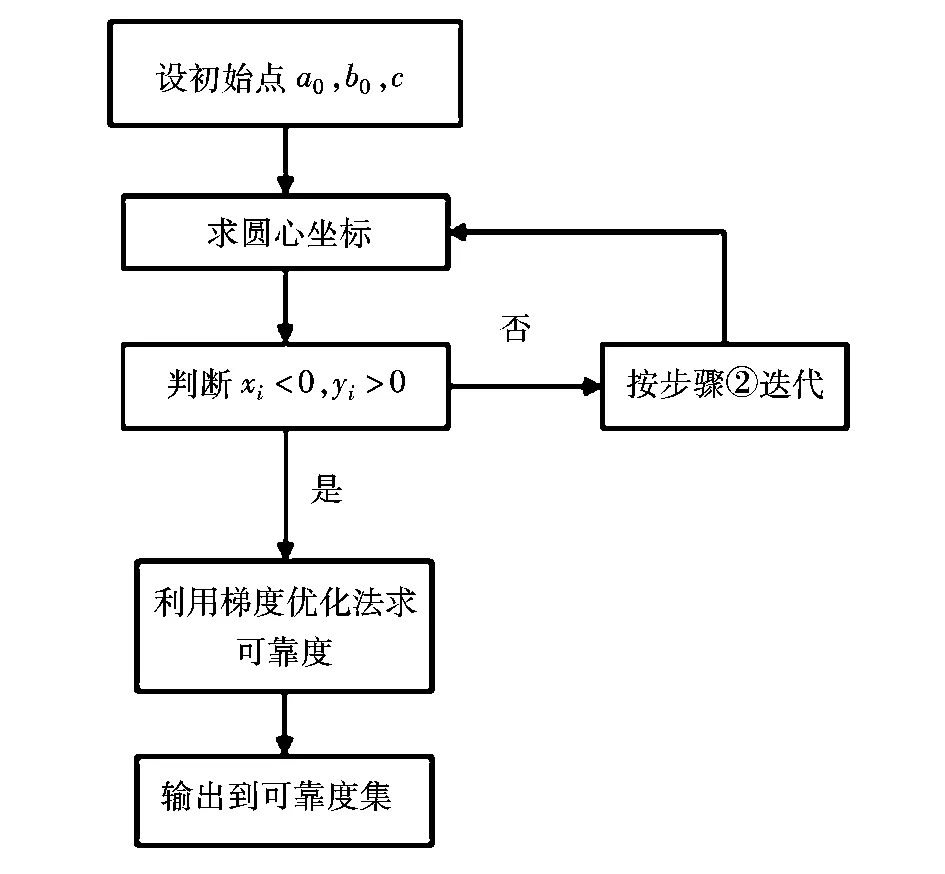
图2　MATLAB搜索流程图Fig.2　Flow chart of MATLAB search

1.3梯度优化法

为简便起见，设基本变量X=(X1,X2,…,Xn)为相互独立的正态变量，同时，引入标准化正态随机变量Y，使得Yi=(Xi-μXi)/σXi,(i=1,2,…,n)。通过变换，可得到一组相互独立的标准正态变量Y=(Y1,Y2,…,Yn)。

于是功能函数即(2)式也可转化到标准正态空间，即

(3)

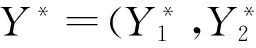
(4)

利用梯度优化法求解(4)式这一优化问题可得验算点Y*，其中所用的迭代格式如下：

(5)

式中，Yi表示第i次迭代计算所求得的验算点；G(Yi)的梯度向量为

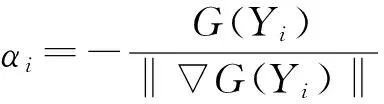
2　基坑整体稳定模糊可靠度分析

传统挡土墙整体稳定性分析是以安全系数来衡量其稳定程度，但此方法忽略了挡土墙稳定性分析中的随机不确定性和模糊不确定性。因此，在可靠度理论分析中同时考虑问题的随机性和模糊性特点则更为科学、全面。

根据模糊数学理论，设Z是描述模糊事件状态的随机变量，其概率密度函数为fZ(z)，μA(z)是描述模糊事件状态程度的隶属函数，则基坑失稳的模糊失效概率为

(6)

相应的模糊可靠度为

(7)

令基坑整体稳定性分析的功能函数为Z=R-S，其中R为结构抗力，S为荷载效应。同时假定c、φ为相互独立的随机变量、结构抗力R和荷载效应S均服从正态分布，则有功能函数Z亦服从正态分布，且概率密度函数为

(8)

其中，μz和σz分别为Z的均值和标准差，可分别按下述公式计算[8]：

(9a)

(9b)

对于隶属函数可选取如式(10)所示的降岭形分布

(10)

对其模糊过渡区上下限的确定可根据模糊类型，结合工程经验和文献[9]选定为a=0.8,b=1.1。

则，将式(8)和式(10)代入式(6)、(7)即可求出整体稳定性的模糊失效概率和模糊可靠度。

3　实例分析

根据文献[10]中的实际工程，某大酒店的基坑开挖深度H=5.78 m，地面均布垂直荷载为q=10 kPa，采用直径为φ=0.8 m的钻孔灌注桩，桩长14 m。为简化起见，桩身所在土层的土性参数粘聚力c、摩擦角φ和土层重度γ可按土层厚度进行加权，统计结果如表1所示。

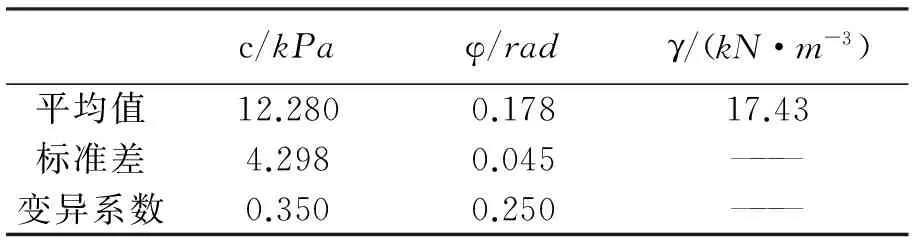
表1　土体参数及概率特征

将实例数据代入MATLAB程序，以及利用Mathematica计算所得的失效概率及各自相应的可靠度如表2所示。其中，根据MATLAB搜索最危险的滑弧所对应的圆心坐标为(-8.16,177.21)，且根据对最危险滑弧面所对应可靠度的迭代计算如表3所示：

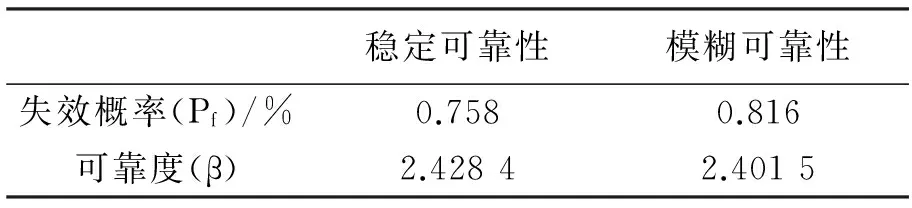
表2　各计算模型所求失效概率及可靠度

表3　最危险滑弧面梯度优化法迭代次数及其稳定可靠度

由于基坑失稳所对应的概率标准目前尚无规定，一般多以10-2～10-3为参考。对比分析表2可知，利用模糊可靠度理论所求得的失效概率较之于利用梯度优化法所求得的失效概率偏大，但两种方法所求得的基坑都是安全的，这与工程实际是相符合的。并且，由表3可知，梯度优化法具有迭代次数少、计算量小的特点。

4　结论

(1)通过MATLAB编程进行最危险滑弧面所对应圆心的全域搜索，使挡土墙整体稳定性问题的研究程序化，提高了挡土墙稳定可靠度计算的精度。从某种程度上，推动了重力式挡土墙整体稳定性的研究。

(2)在简单条分法的基础上，从可靠度的几何意义出发，利用梯度优化法求得相应可靠度，避免了传统方法处理高次非线性问题的误差和发散问题。

(3)对比模糊可靠度和稳定可靠度不难发现：由于模糊可靠度理论既考虑了问题的随机性又考虑了模糊不确定性特点，因此模糊可靠度理论能更科学、全面地反映复杂岩土工程问题的实质,为岩土工程问题研究提供一种新的思路。

[1]BabuGLS，BashaBM.OptimumDesignofCantileverRetainingWallsUsingTargetReliabilityApproach[J].InternationalJournalofGeomechanics, 2008(8)：240-252.

[2] 廖瑛，王月香，华志明.基坑支护方案的改进AHP与多级模糊综合评判[J].地下空间与工程学报,2011,7(4)：706-710.

[3] 赵明华.土力学与基础工程[M].武汉:武汉理工大学出版社， 2012.

[4] 梁大伟，梁仁旺，白晓红.基坑整体稳定性确定最危险滑动面的程序设计[J].山西建筑,2006,32(1)：5-6.

[5] 姜晨光.土力学与地基基础[M].北京：北京化学工业出版社， 2013.

[6] 俞智涛，韩大建.结构可靠度分析的优化算法[J].华南理工大学学报：自然科学版,2003,31(4)：82-84.

[7] 武清玺.结构可靠性分析及随机有限元法[M].北京：机械工业出版社， 2005.

[8] 廖瑛，徐维双.结构基坑土体稳定性的模糊概率分析方法研究[J].工业建筑, 2010,40(6)：85-88.

[9] 何广讷，张彦鹏.基坑支护稳定性的非确值分析[C]∥全国第八届土力学大会论文集.北京:中国建筑工业出版社，1995：503-507.

[10] 宁波市城乡建设委员会.软土地区深基坑支护工程实例[M].北京：中国建筑工业出版社， 1997.

(责任编辑：张英健)

StableReliabilityandFuzzyReliabilityAnalysisofFoundationPitBasedonGradientOptimizationMethod

ZHUHaitao1,2，LIAOYing1，HUANGBin1,3，GUOYufei1，HUANGBo1

1． School of Civil Engineering，Suzhou University of Science and Technology，Suzhou Jiangsu 215011，China;2． School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China;3． School of Civil Engineering，Tongji University，Shanghai 200092，China

Asakindofimportantfoundationpitsupportingstructure,thegravityretainingwallhasalwaysdrawnmanyscholars'attention.Aimingtostartwiththeaspectofthegeometricmeaningofreliability,wecanusetheglobalsearchingmethodofthemostdangerousslidingsurfacecorrespondingtothecenterofthecirclethroughMATLABprogramming,andusethegradientoptimizationmethodtocalculatetheoverallstabilityreliability.Finally,theaccuracyoftheoverallstabilityisimproved.Theresultsofcomparisoncanbeknownthatfuzzyreliabilitytheorycanbemorescientific,comprehensiveandobjectivetoreflecttheessenceofcomplexgeotechnicalengineeringreliabilityproblem.

gradientoptimizationmethod;MATLAB;globalsearch;stablereliability;fuzzyreliability

10.16018/j.cnki.cn32-1650/n.201503017

2015-06-12

朱海陶(1992-)，男，江苏如皋人，硕士生，主要研究方向为非均匀材料和结构的力学行为。

TU476；O159

A

1671-5322(2015)03-0075-04