牵绳非保向力作用下的起重臂稳定性分析

刘士明，陆念力，孟丽霞

(哈尔滨工业大学机电工程学院，150001 哈尔滨)

牵绳非保向力作用下的起重臂稳定性分析

刘士明，陆念力，孟丽霞

(哈尔滨工业大学机电工程学院，150001 哈尔滨)

为准确地分析牵绳非保向力作用下的起重机伸缩臂起升平面外稳定性问题，建立牵绳作用下的多节伸缩臂的挠曲微分方程，引入适当的边界条件，获得多节伸缩臂平面外失稳特征方程的递推表达式，并给出工程起重机常用臂节起升平面外失稳特征方程的显示表达式;讨论牵绳在吊臂方向的投影长度a与吊臂长度l的比值a/l对起重臂失稳临界力的影响.对典型4节起重机伸缩臂进行稳定性分析，与ANSYS密分单元的计算结果比较表明:推导的失稳特征方程是完全正确的;起重臂的抗失稳能力随着a/l比值的逐渐增大而逐渐减弱，并趋于定值.

起重机;稳定性分析;失稳特征方程;多节伸缩臂;变截面阶梯柱

工程起重机作为工业建筑中不可替代的大型吊装设备，其稳定性分析备受学者们关注［1－4］.而轮式起重机由于机动灵活，操作方便，效率高，其应用更加广泛.伸缩臂作为轮式起重机最重要的承载部件，为减轻质量及合理利用材料，通常呈阶梯柱的形式，对于这类结构的稳定性问题，国内外许多学者都进行了深入的研究［5－8］.我国起重机设计规范GB/T 3811—2008中，起重机伸缩臂起升平面外的失稳计算模型为变截面阶梯柱［9］，采用精确有限单元法计算其失稳临界力［10］.文献［11－12］研究了伸缩臂内部支撑油缸对起重臂稳定性的影响，并给出伸缩臂失稳临界力的递推公式.本文作者在上述研究基础上讨论了吊臂间搭接摩擦力对起重臂起升平面外稳定性的影响，并与文献［10］和文献［11－12］的计算结果进行了分析比较［13－14］.对于某些大型轮式起重机，为提高伸缩臂的承载能力，减小伸缩臂挠曲变形，都会在伸缩吊臂上安装牵引钢丝绳或拉索.由于牵引钢丝绳或拉索的存在，使得起重机伸缩臂在起升平面外受非保向力的作用，虽然这些牵绳或拉索引起的非保向力能有效地提高伸缩臂的稳定承载力，但缺乏相应的理论推导.文献［15］虽然研究了平面内单钢丝绳非保向力作用下起重机吊臂的稳定性问题，但该研究只针对吊臂为等截面的情况，对于变截面阶梯柱结构是否适用，有待进一步的分析.

本文详细讨论牵绳等非保向力作用下的多节伸缩臂起升平面外稳定性问题，并分析牵绳在吊臂方向的投影长度与伸缩臂长度的比值对起重机伸缩臂起升平面外失稳临界力的影响.

1 牵绳作用下的起重臂失稳特征方程

牵绳作用下的多节起重机伸缩臂的失稳变形如图1所示，Δ为伸缩臂头部的竖向位移，δ为伸缩臂头部侧向位移，ls为牵绳的长度，a为变形前牵绳在伸缩臂轴向上的投影，h为变形前牵绳在z方向的投影.忽略伸缩臂的轴向变形，令牵绳引起的非保向力为F，由图1可知，其伸缩臂顶部受到的轴向力Fx、侧向力Fy和竖向力Fz分别为

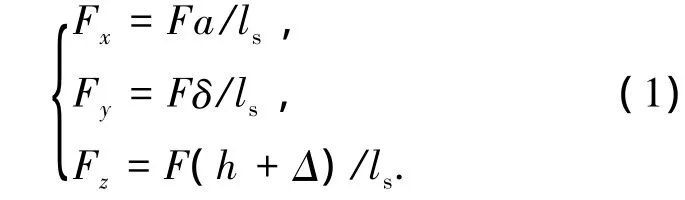
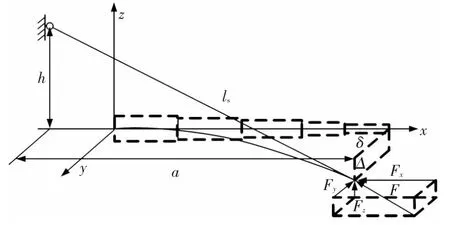
图1 多节起重机伸缩臂的失稳变形图

由图1可知，牵绳作用下的多节伸缩臂平面外失稳力学模型如图2所示，设第i节伸缩臂的截面惯性矩为Ii，xi为第i节伸缩臂顶部到伸缩臂根部的长度，伸缩臂总长为l=xn，E为弹性模量.

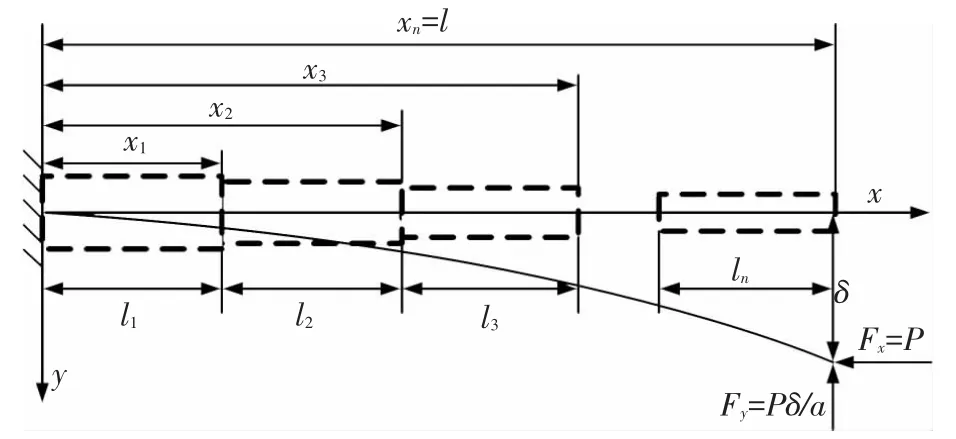
图2 多节起重机伸缩臂的失稳力学模型

将吊臂头部的轴力Fx改用符号P代替，式(1)中的侧向分力可表示为

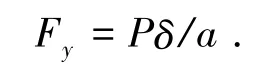
由图2所示的多节伸缩臂失稳力学模型，可

建立各节伸缩臂挠曲微分方程为

挠曲微分方程(3)的通解可表示为

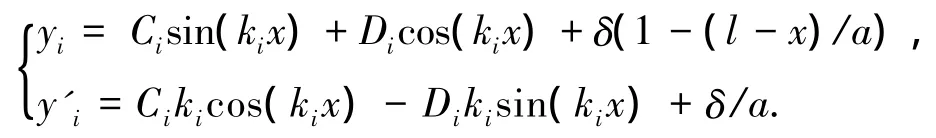
由伸缩臂根部的边界条件x=0时，y1=y'1=0，得

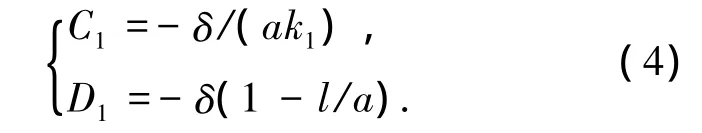
又由位移边界条件 x=xi时，yi=yi+1，y'i=y'i+1得各积分常数之间的关系为

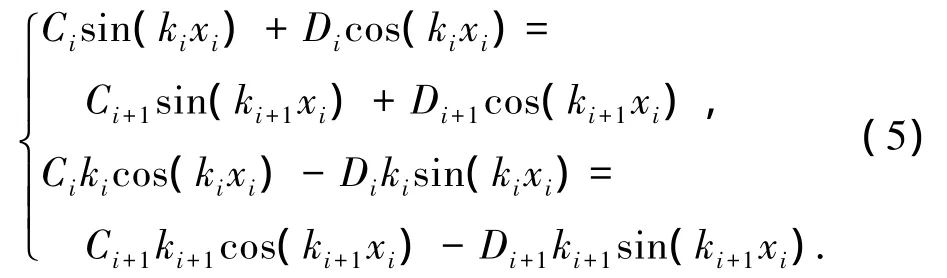
将式(5)整理得积分常数之间递推表达式:

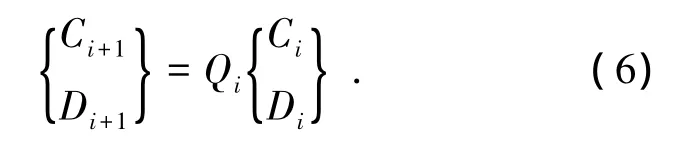
式(6)中Qi可表示为

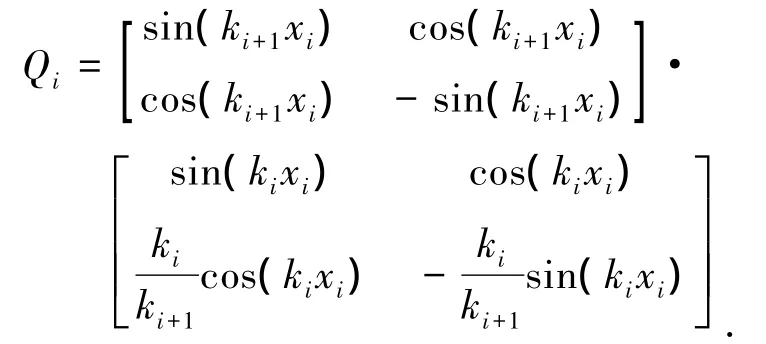
由式(6)得积分常数Cn和Dn的表达式:

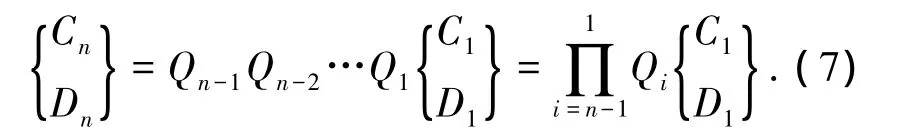
由伸缩臂顶部边界条件x=xn=l时，yn=δ得

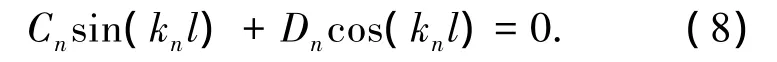
将式(7)代入式(8)得伸缩臂失稳特征方程:

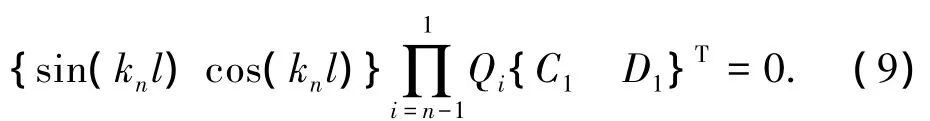
将式(4)代入式(9)中，且由于侧向位移δ为任意数值，故多节伸缩臂的失稳特征方程变为

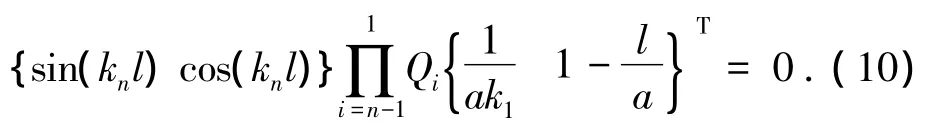
失稳特征方程(10)是以P为未知量的非线性超越方程，解此超越方程即可得结构的失稳临界力Pcr.当多节伸缩臂具有相同的截面惯性矩，即伸缩臂为等截面的极限情况，其失稳特征方程(10)可退化为与文献［9］和文献［15］具有相同的表达形式:

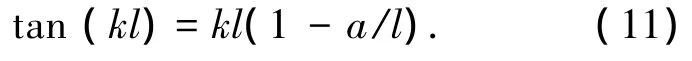
由失稳特征方程(10)和式(11)可知，单根钢丝绳对伸缩臂平面外稳定性的影响仅与钢丝绳在伸缩臂方向的投影长度a和伸缩臂的长度l的比值a/l有关.

2 起重臂失稳特征方程的显示表达

为了便于工程实际中指导起重机结构设计人员对牵绳作用下的伸缩臂进行稳定性分析，本文将给出工程中多节起重机常用臂节的平面外失稳特征方程的显示表达式.

当n=1时，失稳特征方程式(10)可表示为

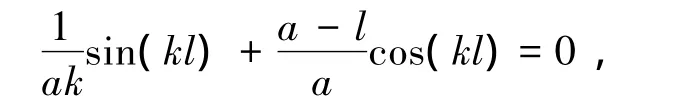
或表示为

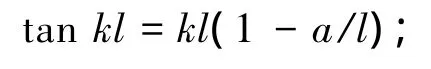
当n=2时，起重臂的失稳特征方程可表示为

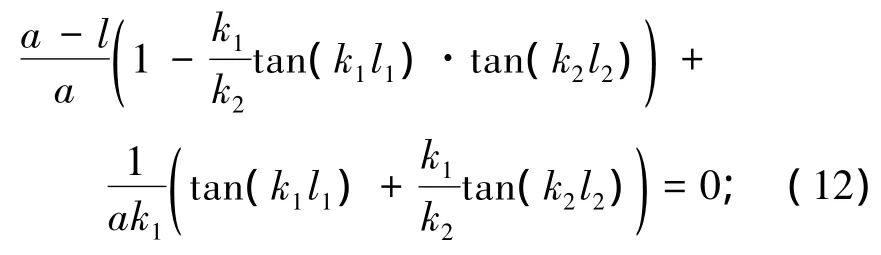
当n=3时，起重臂的失稳特征方程可表示为

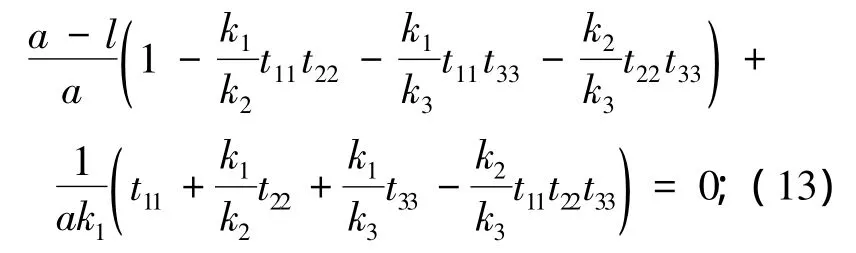
当n=4时，起重臂的失稳特征方程可表示为

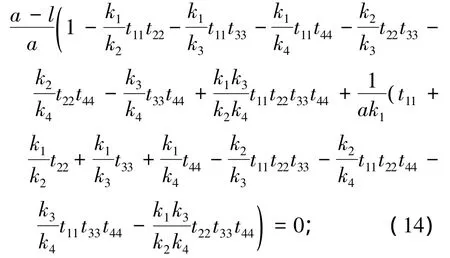
当n=5时，起重臂的失稳特征方程可表示为

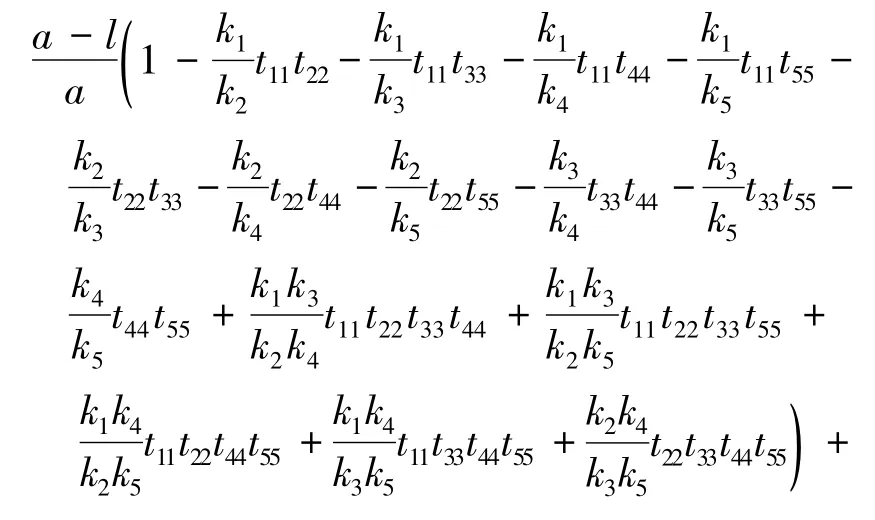
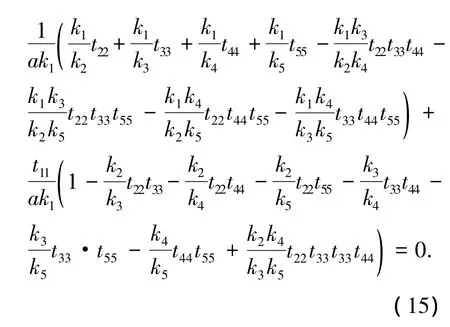
式(12)～式(15)中，tii=tan(kili)，li表示各节伸缩臂的长度，如图2所示，即 l1=x1，li=xi-xi-1.

式(12)～式(15)分别表示起重机有2、3、4、5节伸缩臂时的平面外失稳特征方程的显示表达式.

3 起重机伸缩臂平面外稳定性分析实例

为了分析牵绳或拉索等非保向力对起重机伸缩臂稳定性的影响，针对牵绳作用下的典型4节起重机伸缩臂进行平面外稳定性分析.通常欧拉临界力可表达式为Pcr=π2EI/(μl)2，为了便于分析比较，采用量纲一的失稳计算长度系数μ来表示起重臂的抗失稳能力.

算例 图3所示为牵绳作用下4节起重机伸缩臂模型，伸缩臂的总长度为l，各节伸缩臂长度l1=0.34l，l2=0.22l，l3=0.22l，l4=0.22l，牵绳在伸缩臂方向投影长度为a，截面惯性矩比值为I1/I2=1.3，I2/I3=1.9，I3/I4=2.5.

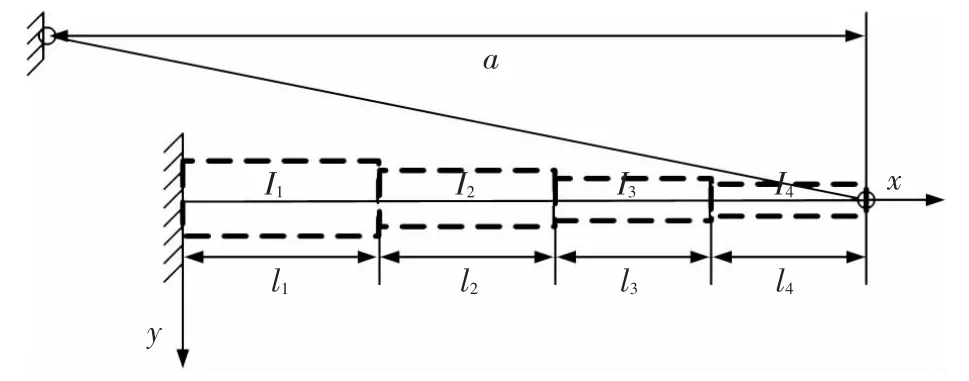
图3 牵绳作用下的4节伸缩臂模型

由失稳特征方程式(10)和式(11)可知，牵绳作用下的伸缩臂失稳临界力仅与长度比值a/l有关，将不同长度比值代入4节伸缩臂的显示失稳特征方程(14)，可得用惯性矩I1表示的失稳计算长度系数μ=π/(k1l).同时为验证本文理论推导的正确性，采用有限元分析软件ANSYS进行验证，分别采用Beam44单元和Link10单元来模拟伸缩臂和牵绳，每节伸缩臂划分为20个单元，其计算结果列于表1，表中阶梯柱代表无牵绳作用时伸缩臂的失稳计算长度系数.

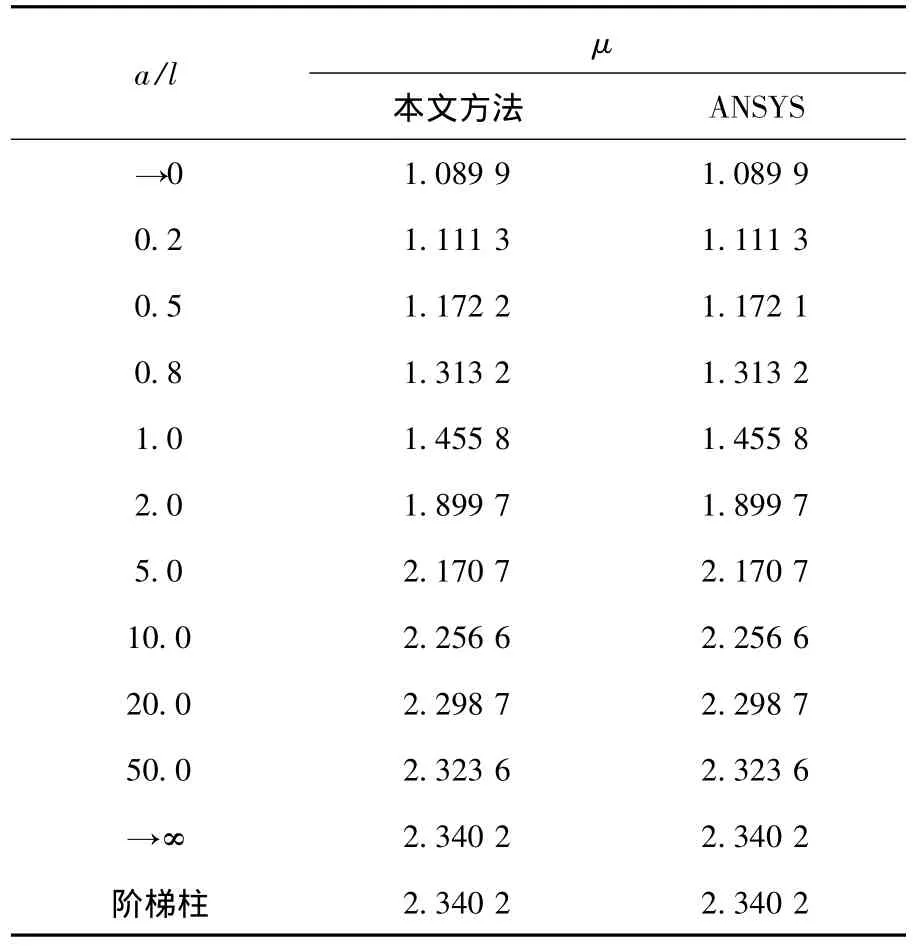
表1 不同长度比值的计算长度系数

由表1可知，本文与ANSYS计算结果在小数点后四位完全相同，验证了本文理论推导的正确性及求解的精确性.同时还可以看出，随着长度比值a/l的逐渐增大，其失稳计算长度系数μ逐渐增大，即结构的失稳临界力逐渐减小，抗失稳能力变弱.当a/l→∞ 时，其失稳计算长度系数μ与没有牵绳时相等，此时可认为牵绳对起重机伸缩臂平面外的稳定性没有影响.

4 结论

1)分析了牵绳或拉索等引起的非保向力作用下的多节起重机伸缩臂平面外稳定性，给出了起重臂失稳特征方程的递推表达式;并结合起重机设计规范，给出了2～5节伸缩臂失稳特征方程的显示表达式，为起重机设计规范GB/T 3811—2008的修订提供理论依据.

2)比较本文计算结果与ANSYS密分单元的计算结果表明，本文针对牵绳非保向力作用下的起重臂平面外失稳问题的理论推导是正确的，用该理论公式求解起重臂的起升平面外的失稳临界力是精确的.

3)对典型4节起重臂稳定性算例分析表明，随着长度比值a/l的逐渐增大，起重臂的平面外失稳计算长度系数μ逐渐增大，并趋于定值，即非保向力对起重臂稳定性的影响随着a/l的增大而减弱.

［1］FRASER D J，BRIDGE R Q.Buckling of stepped crane columns［J］.Journal of Constructional Steel Research，1990，16(1):23－38.

［2］SIMAO P D，COELHO A M，BIJLAARD F S K.Stability design of crane columns in mill buildings［J］.Engineering Structures，2012，42:51－82.

［3］WANG Anlin，JIANG Tao，DONG Yaning，et al.Study on structural instability of large crawler crane boom structure［C］//2009 3rd International Conference on Techning and ComputationalScience.Heideberg:Springer Verlag，2012:401－406.

［4］张宏生，陆念力.动臂式塔机变截面吊臂的整体稳定性分析［J］.哈尔滨工业大学学报，2010，42(9):1394－4397.

［5］ZHANG Hongsheng，LU Nianli，LAN Peng.Buckling of stepped beams with elastic supports［J］.Journal of Harbin Institute of Technology，2009，16(3):436－440.

［6］LI Q S.Buckling of multi-step non-uniform beams with elastically restrained boundary conditions［J］.Journal of Constructional Steel Research，2001，57(7):753－777.

［7］PARK J S，STALLINGS J M.Lateral-torsional buckling of stepped beams［J］.Journal Structural Engineering，2003，129(11):1457－1465.

［8］PARK J S，STALLINGS J M.Lateral-torsional buckling of stepped beams with continuous bracing［J］.Journal of Bridge Engineering，2005，10(1):87－95.

［9］中国国家标准化管理委员会.GB/T 3811—2008.起重机设计规范［S］.北京:中国标准出版社，2008:181－183.

［10］陆念力，兰朋，白桦.起重机箱形伸缩臂稳定性分析的精确理论解［J］.哈尔滨建筑大学学报，2000，33(2):89－93.

［11］张月红.具有油缸支撑的起重机箱形伸缩臂的稳定性研究［D］.哈尔滨:哈尔滨工业大学，2007:14－23.

［12］LU Nianli，ZHANG Hongsheng，LAN Peng.Precise theoretical solution of Euler’s critical load for crane telescopic boom with cylinder supporting［C］//Proceedings of the 2007 International Conference on Advancesin Construction Machinery and Vehicle Engineering.Shanghai:Tongji University Press，2007:527－530.

［13］LIU S M，LU N L，WANG B.Comparison of three calculation models on overallstability analysis of telescopic boom with built-in cylinder［C］//Proceedings 2010 International Conference on Digital Manufacturing and Automation.Changsha:［s.n.］，2010:400－404.

［14］刘士明.计及臂间搭接与摩擦影响的箱形伸缩臂整体稳定性研究［D］.哈尔滨:哈尔滨工业大学，2008:10－24.

［15］孟晓平，陆念力，李良.非保向力作用下起重机吊臂起升平面外整体稳定特征方程及应用［J］.哈尔滨建筑大学学报，1997，30(2):99－103.

Stability analysis of telescopic booms under pull-rope follower force

LIU Shiming，LU Nianli，MENG Lixia

(School of Mechatronics Engineering，Harbin Institute of Technology，150001 Harbin，China)

To solve the out-of-plane stability problem of the telescopic boom subjected follower forces，the deflection differential equations of the multi-telescopic boom model which under actions of pull-rope are established.With proper boundary conditions，the recurrence formulas of buckling characteristic equations are presented，and the explicit expressions of the boom in some practical applications are given.The influence on destabilizing critical force of telescopic boom due to the ratio of a/l is discussed in detail，where a is the length of wire projected to telescopic boom，and l is the length of telescopic boom.In comparison with the ANSYS method，the results show that the buckling characteristic equations are completely correct.As the ratio of a/l increases，the capacity of anti buckling reduces and tends to be a constant value.

crane;stability analysis;buckling characteristic equation;multi-section telescopic boom;stepped column

TH213;O317

A

0367－6234(2014)03－0026－04

2013－03－29.

国家科技支撑计划资助项目(2008BAJ09B01－03).

刘士明(1983—)，男，博士研究生;

陆念力(1955—)，男，教授，博士生导师.

刘士明，lsm831206@163.com.

(编辑 杨 波)