利用改进开窗转换法确定沥青离散松弛时间谱

陈静云，孙依人，徐 辉，张 岩

(大连理工大学交通运输学院，116024 辽宁大连)

利用改进开窗转换法确定沥青离散松弛时间谱

陈静云，孙依人，徐 辉，张 岩

(大连理工大学交通运输学院，116024 辽宁大连)

为了精确地获得沥青胶结料的离散松弛时间谱，提出了一种改进开窗转换法的线性黏弹性材料函数转换算法.此方法可以用于离散延迟时间谱和离散松弛时间谱的相互转换.与开窗转换法相比，改进开窗转换法对于时间常数的设置更加精确，并且不会产生负数谱线.将改进开窗转换法用于一种传统非改性沥青的弯曲梁流变仪试验数据的离散延迟时间谱的转换，成功地确定了相应的离散松弛时间谱.经有限元模型验证表明，此离散松弛时间谱能很好地还原该沥青结合料的应力松弛特性.

改进开窗转换法;黏弹性;蠕变试验;Prony级数

沥青是沥青混合料黏弹性的直接来源，且沥青路面的车辙、疲劳开裂、温度裂缝等病害都与沥青的黏弹性有关，因此研究沥青在不同激励下产生的黏弹性响应对于沥青路面的结构设计和病害预防有很好的参考价值.蠕变和应力松弛是黏弹性材料力学响应随时间变化的两个重要特征.弯曲梁流变仪(bending beam rheometer，BBR)为沥青静态蠕变行为的研究提供了有效途径，通过BBR试验可以获得沥青的离散延迟时间谱.文献［1-4］对沥青蠕变性能进行了深入的研究.对于沥青的松弛模量，可通过直接施加瞬态矩形应变荷载得到，但由于设备的限制，试验操作困难，若利用松弛试验直接测定，会造成较大误差.因此，通常采用对延迟函数的转换间接地获得.文献［5-13］提出了多种关于松弛函数和延迟函数相互转换的数值或解析方法，其中 Tschoegl和 Emri［13］提出的开窗转换法(windowinginterconversion method)是较为简单实用的一种.但由于该方法近似地将时间常数(松弛时间ρi或者延迟时间τi)等距设置，且假设ρi=τi，因此转换后可能产生负数谱线.为了避免这种情况的发生，本文提出了一种基于时间常数精确设置的改进开窗转换法(improved windowing interconversion method)，并用此方法成功确定了某沥青结合料的离散松弛时间谱.应用离散松弛时间谱，可以进一步对沥青的动、静态松弛性能进行研究.

1 模型理论

材料应力松弛行为通常采用广义Maxwell模型描述.广义Maxwell模型由一系列简单Maxwell元件并联得到，由此模型推导出松弛模量的Prony级数表达式为

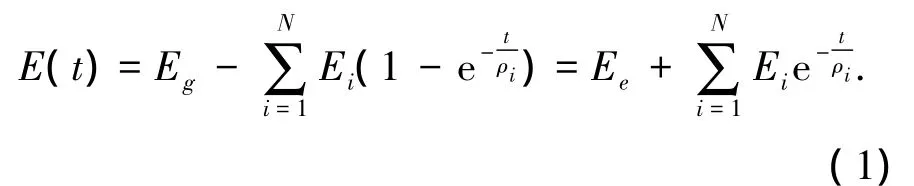
式中:Eg为玻璃态模量，即瞬态模量;Ee为平衡模量;Ei为松弛强度;ρi为松弛时间;(Ei，ρi)为离散松弛时间谱.

材料蠕变行为用广义Kelvin模型描述更为简单.广义Kelvin模型由一系列简单Kelvin元件串联而成，由此推导出蠕变柔量的Prony级数表达式为

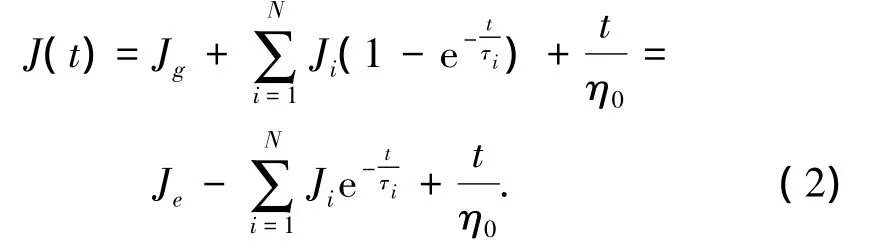
式中:Jg为玻璃态柔量，即瞬态柔量;Je为平衡柔量;Ji为延迟强度;τi为延迟时间;(Ji，τi)为离散延迟时间谱;η0为长期黏度.

当材料为黏弹性固体时，Ee＞0且η0→∞.对式(1)、(2)进行Carson变换，即乘s的Laplace变换，s为复数变量，可将松弛函数和延迟函数从时域变换到复数平面内，表示为

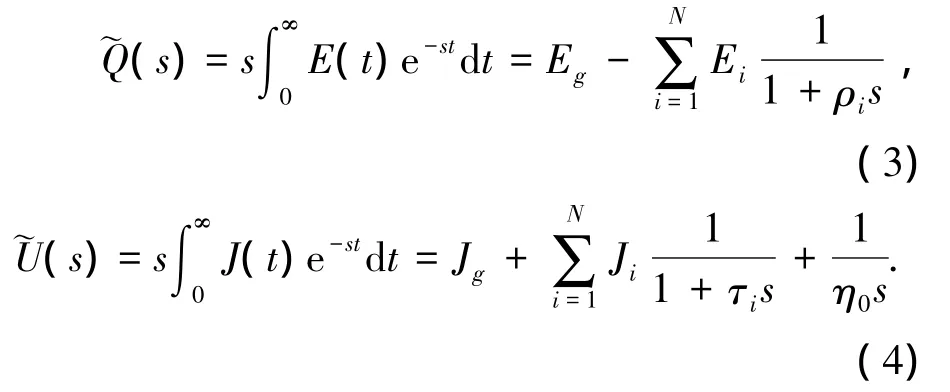
由弹性-黏弹性对应原理可知，在复数平面内松弛函数和延迟函数具有与弹性材料类似的倒数关系，即

2 试 验

2.1 BBR试验

BBR由加载装置、乙醇冷却浴和计算机数据采集系统组成.在对沥青小梁试件进行静载三点弯曲蠕变试验的过程中，数据采集系统可以自动测量小梁跨中处的荷载和挠度值，并由数据处理程序计算出蠕变劲度S和蠕变劲度变化率m两个参数.这两个参数反映了沥青结合料的松弛性能和低温抗裂能力.在静载作用下，蠕变劲度S(t)为蠕变柔量J(t)的倒数，即

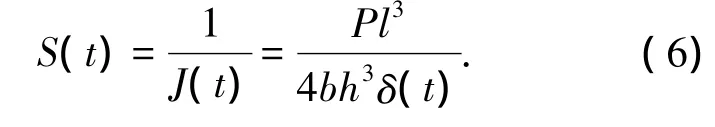
式中:P为恒定荷载，取0.98 N;b为小梁宽度，取12.7 mm;h 为小梁高度，取6.35 mm;L 为简支梁跨径，取101.6 mm;δ(t)为小梁跨中挠度.对90#基质沥青分别进行-6、-12、-18、-24℃下的BBR试验，通过式(6)计算出各温度下的蠕变柔量J(t)，如图1所示.

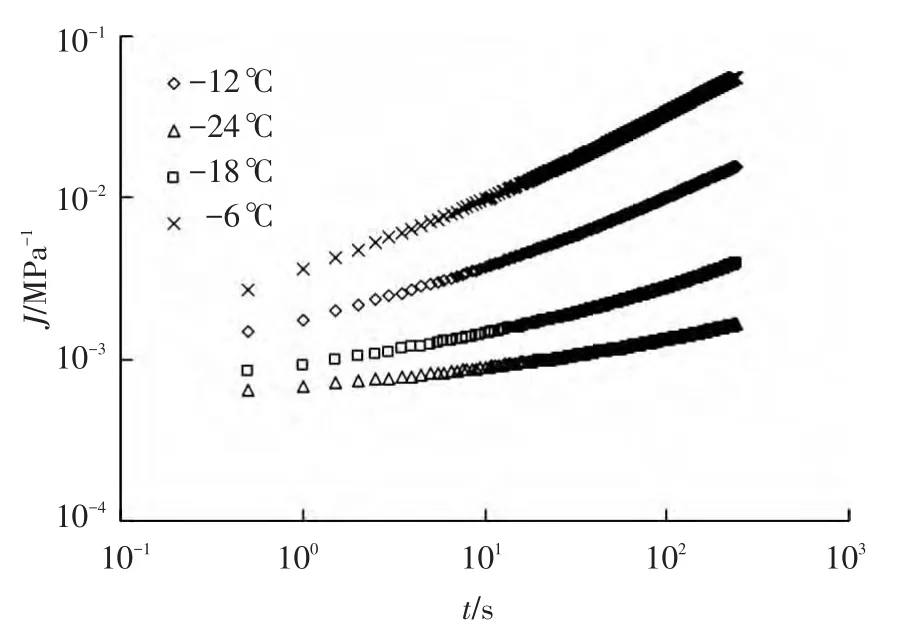
图1 不同温度下的蠕变柔量试验数据

2.2 蠕变柔量主曲线和WLF方程

沥青是典型的热流变简单材料，具有明显的温度依赖性和时间依赖性，符合时温等效原理.因此，可将不同温度下的蠕变柔量曲线在时间的对数坐标下进行平移，进而得到参考温度下的蠕变柔量主曲线.利用蠕变柔量主曲线可以对沥青的长期蠕变性能进行预测，而不必进行长时间的实际试验.本文参考温度取为-12℃，得到相应的蠕变柔量主曲线如图 2 所示，-6、-12、-18、-24 ℃下的时间-温度移位因子分别为-0.965、0、1.328、2.466.通过对时间-温度移位因子进行非线性最小二乘拟合，可以得到不同温度下的时间-温度移位因子.拟合方程通常有两种形式:Williams-Landel-Ferry(WLF)方程和 Arrhenius 方程［1］.本文采用WLF方程，表达式为

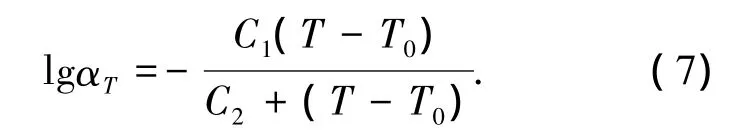
式中:lg αT为时间 -温度移位因子，C1、C2为材料参数，T0为参考温度.当T0=-12℃ 时，非线性拟合结果为 C1=8.82，C2=49.86.平移后的缩减时间为 ξ=t/αT.

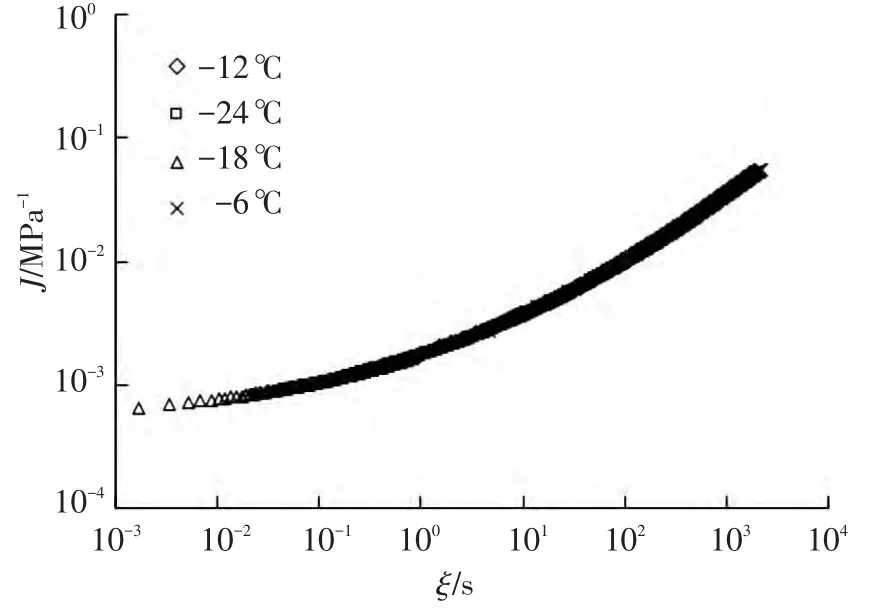
图2 参考温度为－12℃的蠕变柔量主曲线

2.3 离散延迟时间谱的识别

离散延迟时间谱的识别本质上是对蠕变柔量主曲线进行Prony级数拟合的过程.本文根据文献［14］介绍的方法，采用广义Kelvin模型，获得了该90#基质沥青的离散延迟时间谱，如表1所示，相关系数为 0.999 6.

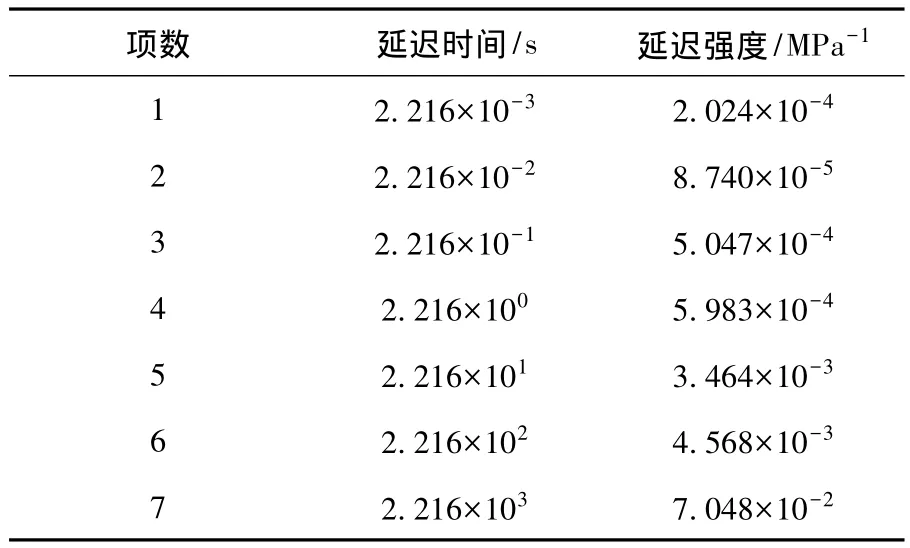
表1 离散延迟时间谱

3 离散松弛时间谱的确定

3.1 开窗转换法

Tschoegl和Emri提出了一种叫做开窗转换法的计算机递归算法，可以对黏弹性材料的离散松弛时间谱和离散延迟时间谱进行相互转换.该方法的提出是基于以下事实:复数域内的松弛函数和延迟函数的核函数1/(1+τis)，在以s=1/τi为中心的一个十倍程内随时间变化最为显著，因此把这个十倍程定义为边界窗(boundary window).当一个十倍程内包含n(n≥1)个时间常数τi的倒数时，将［sl，su］(即模拟最有效的区间)定义为模拟窗(modeling window).模拟窗受边界窗的限制，当n=1时，二者重合.开窗转换法以式(5)为转换桥梁，计算每条谱线时只采用相应模拟窗内的试验数据，且假设ρi=τi.在计算前需要预先设置1/τi，每个十倍程内等距设置n个时间常数的倒数.下面以由离散延迟时间谱确定离散松弛时间谱为例，对开窗转换法的基本步骤进行简要说明.

首先，由式(4)生成一组延迟数据{˜Uj，sj;j=1，…，M}，并通过式(5)得到相应的一组松弛数据{˜Qj，sj;j=1，…，M}.然后，分别将松弛数据和谱线强度进行标准化处理为

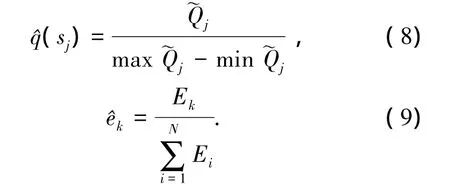
得到松弛函数表达式为

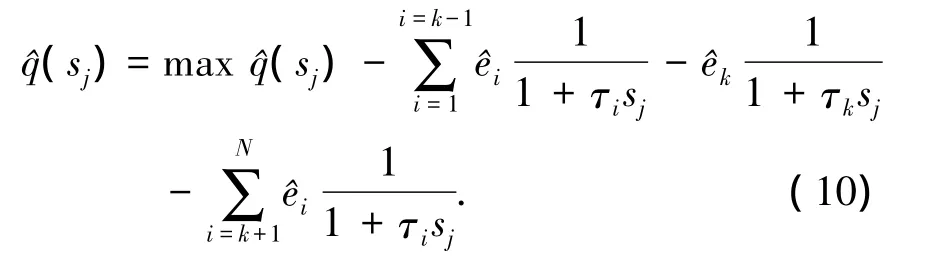
引入数据点和松弛函数间的绝对误差Δj，并用模拟窗内的Mw个数据点形成平方误差函数fk为

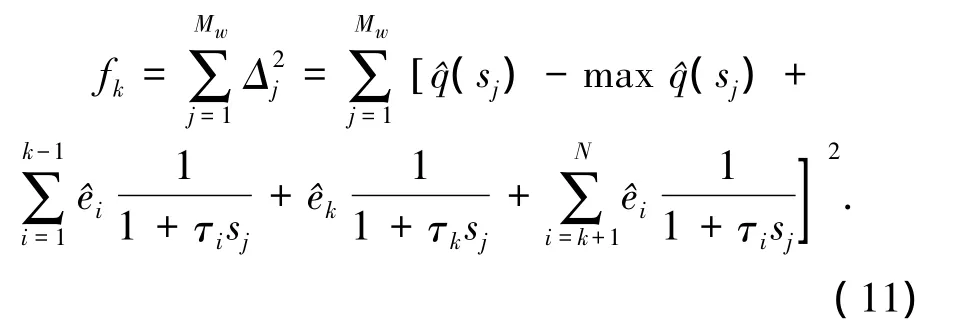
使平方误差函数fk最小化，进而导出标准化谱线强度为

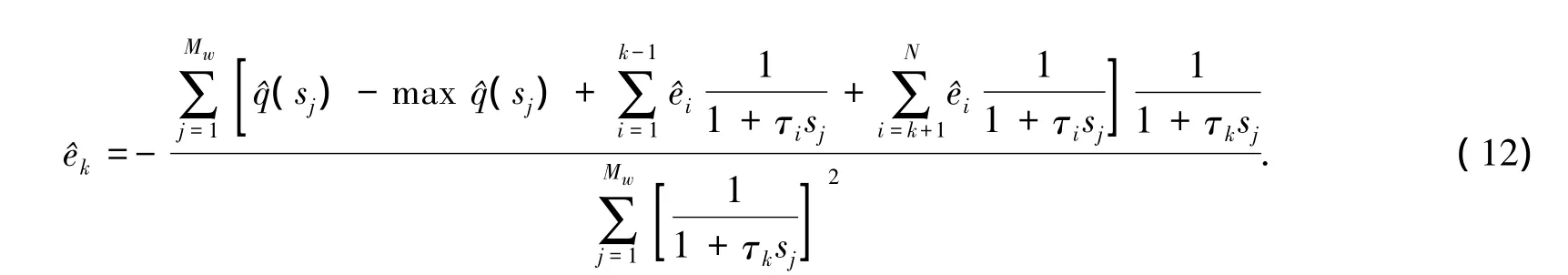
计算时从第1条谱线开始，依次向后计算谱线强度.在进行第1次数据扫描时，将标准化谱线强度初值设为0，在接下来的扫描中，将得到的非负谱线强度保留，同时将得到的负谱线强度重新设置为0.当相邻扫描计算出的两组标准化谱线强度差的范数小于某给定标准值时，终止迭代.最后，谱线强度可由标准化谱线强度求得.

3.2 改进开窗转换法

开窗转换法虽然简单直接，但由于时间常数等距设置，且假设ρi=τi，转换后可能产生负数谱线.为了避免负数谱线的产生，本文提出了一种基于时间常数精确设置的改进开窗转换法.仍以获得离散松弛时间谱为例.由式(5)可知

对于某给定的τk，可以通过求解式(14)的根的负倒数获得相应的ρk.为了求解式(14)的根，文献［10］描述了一种实用的寻根图解方法:以延迟函数绝对值的对数作为纵坐标，以-1/s(s＜0)的对数作为横坐标，采用0.01个十倍程作为横坐标取值间隔作图(取值间隔可调节)，图中最大值的横坐标即为τi，而最小值的横坐标即为所求松弛时间ρi.由于改进开窗转换法设置的松弛时间ρi分布是基于松弛函数与延迟函数的精确数值关系，因此计算不会产生负数谱线.同理，可以从松弛时间分布获得延迟时间分布.

3.3 转换结果

采用改进开窗转换法，以寻根图解法计算出的精确松弛时间分布代替原开窗转换法中近似的等距分布，利用Matlab软件编制计算程序，对表1所示离散延迟时间谱进行转换，成功获得了对应的离散松弛时间谱，如表2所示，相关系数为0.999 9.寻根图解法得到的时间常数分布如图3所示.

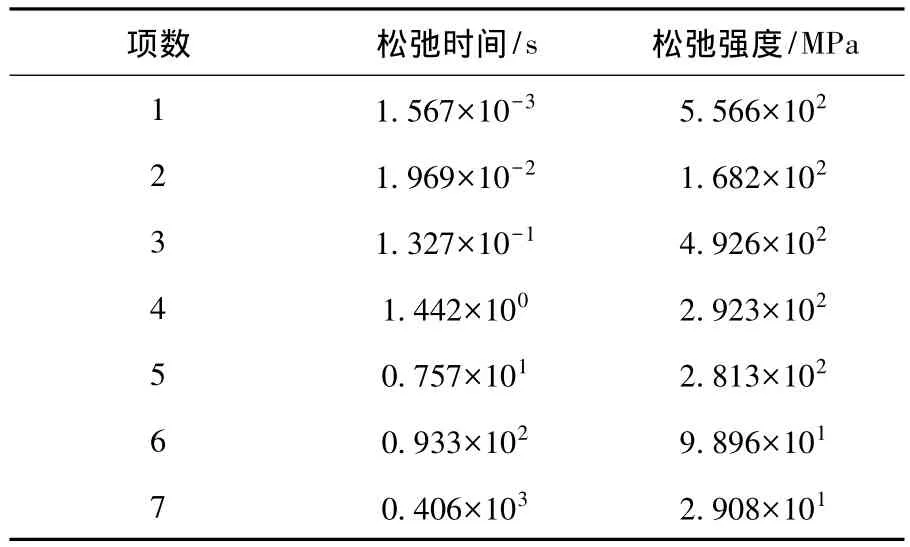
表2 离散松弛时间谱

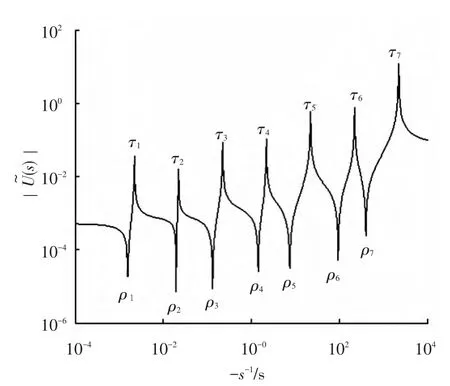
图3 时间常数分布

4 离散松弛时间谱的验证及应用

为了验证采用改进开窗转换法获得的离散松弛时间谱的可靠性，利用ANSYS有限元程序建立了尺寸为h×L的BBR沥青小梁二维有限元模型.采用表2数据作为有限元模型的黏弹性材料参数，将黏弹性泊松比近似取为0.49，单元取为PLANE182平面应力单元，对不同温度下的BBR试验进行模拟，并将模拟数据与试验数据进行了比较，结果如图4所示.由图可知，无论加载过程还是卸载过程模拟数据与试验数据均非常接近，由此可知采用改进开窗转换法获得的离散松弛时间谱能准确地反映该沥青结合料的应力松弛特性.

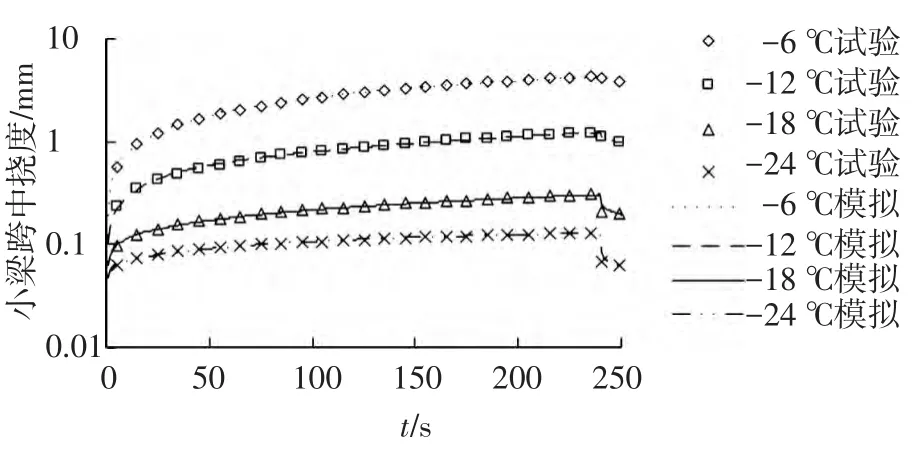
图4 模拟数据与试验数据的比较

在确定沥青离散松弛时间谱后，可以方便地获得相应的松弛模量E(t)、储能模量E'(ω)和耗散模量E″(ω)(ω为加载频率)，进而预测沥青的动、静态松弛性能.由此可知，离散松弛时间谱包含了给出谱线范围内材料线性黏弹性的所有信息，是一种良好的预测沥青黏弹性能的方法.

5 结论

1)采用BBR对某90#基质沥青进行了不同温度下的BBR静载弯曲蠕变试验，获得了参考温度为-12℃的静态蠕变柔量主曲线和时间-温度移位因子，并通过非线性拟合分别得到了该沥青结合料的离散延迟时间谱和WLF方程.

2)在原有开窗转换算法的基础上，提出了一种基于时间常数精确设置的改进开窗转换算法.该算法不会产生物理上无法解释的负数谱线.将改进开窗转换法用于由BBR试验获得的离散延迟时间谱的转换，成功获得了该沥青结合料的离散松弛时间谱，并由有限元模型验证了该离散松弛时间谱的可靠性.

3)利用离散松弛时间谱可以进一步预测沥青动、静态松弛性能，这对于降低试验成本和研究沥青黏弹性能均有重要意义.

［1］张肖宁.沥青与沥青混合料的粘弹力学原理及应用［M］.北京:人民交通出版社，2006.

［2］詹小丽，张肖宁，王端宜，等.基于动态蠕变性能的沥青延迟时间谱研究［J］.中国公路学报，2008，21(2):34-38.

［3］詹小丽，张肖宁，卢亮.沥青低温粘弹性能的预测［J］.吉林大学学报:工学版，2008，38(3):530-534.

［4］郑健龙，吕松涛，田小革.基于蠕变试验的沥青粘弹性损伤特性［J］.工程力学，2008，25(2):193-196.

［5］LUK-CYRJ， CROCHONT， CHUNL， etal.Interconversion of linearly viscoelastic material functions expressed as Prony series:a closure［J］.Mechanics of Time-Dependent Materials，2013，17(1):53-82.

［6］KATICHA SW， FLINTSCH G W.Fractional viscoelastic models: master curve construction，interconversion，and numericalapproximation ［J］.Rheologica Acta，2012，51(8):675-689.

［7］ANDERSSEN R S，DAVIES A R，DE HOOG F R.The effect of kernel perturbations when solving the interconversion convolution equation of linear viscoelasticity［J］.Applied Mathematics Letters，2011，24(1):71-75.

［8］MUN S，ZI G.Modeling the viscoelastic function of asphaltconcrete using a spectrum method ［J］.Mechanics of Time-Dependent Materials，2010，14(2):191-202.

［9］HU S，ZHOU F.Development of a new interconversion tool for hot mix asphalt(HMA)linear viscoelastic functions［J］.Canadian Journal of Civil Engineering，2010，37(8):1071-1081.

［10］PARK SW， SCHAPERY R A.Methodsof interconversion between linearviscoelastic material functions:a numerical method based on Prony series［J］.International Journal of Solids and Structures，1999，36:1653-1675.

［11］BRADSHAW R D，BRINSON L C.A sign control method for fitting and interconverting material functions for linearly viscoelastic solids［J］.Mechanics of Time-Dependent Materials，1997，1(1):85-105.

［12］MEAD D T.Numerical interconversion of linear viscoelastic material functions［J］.Journal of Rheology，1994，38(6):1769-1795.

［13］TSCHOEGL N W，EMRI I.Generating line spectra from experimental responses: interconversion between relaxation and retardation behavior［J］.International Journal of Polymeric Materials，1992，18:117-127.

［14］EMRI I，TSCHOEGL N W.Generating line spectra from experimental responses:relaxation modulus and creep compliance［J］.Rheologica Acta，1993，32:311-321.

Determination of discrete relaxation time spectra of asphalt utilizing improved windowing interconversion method

CHEN Jingyun，SUN Yiren，XU Hui，ZHANG Yan
(School of Transportation ＆ Logistics，Dalian University of Technology，116024 Dalian，Liaoning，China)

To accurately obtain discrete relaxation time spectra of asphalt binders，an algorithm termed the improved windowing interconversion method(IWIM)is presented in this paper.The IWIM allows discrete retardation time spectra to be converted into discrete relaxation time spectra，and vice versa.Compared with the windowing interconversion method(WIM)，the IWIM affords a more exact distribution of time constants without generating negative spectrum lines.The IWIM was applied to the discrete retardation time spectrum of bending beam rheometer(BBR)test data for a conventional unmodified asphalt binder，successfully determining the discrete relaxation time spectrum.The result of the validation by means of a BBR test finite element simulation shows that the discrete relaxation time spectrum from the IWIM can well reproduce the stress relaxation properties of the asphalt binder.

improved windowing interconversion method;viscoelasticity;creep test;Prony series

U414

A

0367-6234(2014)02-0104-05

2013-03-26.

国家自然科学基金资助项目(50578031).

陈静云(1956—)，女，教授，博士生导师.

陈静云，chenjy@dlut.edu.cn.

(编辑 魏希柱)