无粘性土的地震主动土压力水平层法改进

黄 睿，夏唐代

(浙江大学软弱土与环境土工教育部重点实验室，310058 杭州)

无粘性土的地震主动土压力水平层法改进

黄 睿，夏唐代

(浙江大学软弱土与环境土工教育部重点实验室，310058 杭州)

为了研究主应力偏转对土压力的影响，基于拟静力法，考虑平移模式下挡土墙墙后土体的主应力偏转和土层间的水平剪力，改进水平层分析法，根据应力状态和静力平衡条件建立基本方程组，通过迭代搜索程序进行求解，计算得出滑裂面形状、地震主动土压力分布、土压力系数和合力作用点，并对其进行参数讨论.结果表明:对于无粘性土，搜索得到的滑裂面曲线形状近似直线，故简化计算时，采用平面滑裂面的假设比较合理;填土内摩擦角和水平地震作用对土压力分布的影响较大，墙土摩擦角和竖向地震作用影响相对较小.与传统拟静力法对比，两种方法所得的土压力分布基本吻合，但是，改进水平层法所得的曲线呈现非线性变化趋势.

地震;土压力;水平层法;主应力偏转

挡土墙的土压力作为土力学的经典问题，一直受到很多工程和科研人员的关注，其计算的关键问题在于确定作用在墙背上的侧土压力性质、大小、方向和作用点，经典的库伦理论和朗肯理论已经可以基本满足工程需要，但是，地震作用时，挡土墙的土压力计算却是一个比较复杂的问题，相关的理论研究还不完善.目前，国内外普遍采用的计算方法是基于库伦理论演化出的Mononobe-Okabe拟静力法，即用惯性力考虑地震作用，以静力学的方法来近似处理动力学的问题，该方法思路清晰，计算简便，被看作研究地震作用下土压力的基本理论.文献［1－3］提出采用水平层分析法计算土压力和侧压力系数，并基于拟静力法，对地震下的土压力分布进行探讨.文献［4－5］在此基础上利用水平层法对倾斜挡土墙背等复杂工况的地震土压力进行了深入研究.文献［6－8］根据水平土层的静力和力矩平衡建立基本方程组，对挡土墙和边坡的地震土压力问题进行了求解.

然而，已有的地震土压力研究很少考虑土拱效应引起的主应力偏转影响，而当土体与结构之间存在摩擦作用时，必定有土拱效应，进而会改变土中主应力的方向，影响土压力的分布.文献［9－11］通过预先假设土拱曲线的形状，对土拱效应下平面滑裂面的主动、被动土压力分布进行了一系列理论性分析.文献［12－13］针对上述方法中土层单元无法满足静力平衡的不足，将土体的应力分析和水平层的静力平衡条件相结合，提出考虑主应力偏转的土压力计算改进方法，并与经典土压力和试验结果进行对比.

本文基于前人研究成果，以平移模式下的刚性挡土墙后的无粘性土为研究对象，考虑土拱效应对主应力偏转的影响，事先并不假定滑裂面的形状，而通过土体的应力分析和水平单元层的静力平衡条件建立基本方程，得到每个水平单元层关于各层的主应力和滑裂面倾角的隐式方程组，由于在土拱的实际形成过程中，挡土墙和基底土体对滑动土体有约束作用，水平土层之间的剪应力必定客观存在，故基本方程中加入水平剪力部分.通过编程，对多层水平单元的土压力进行迭代搜索计算，求出滑裂面的形状，土压力的分布，土压力系数和合力作用点，并讨论了土体内摩擦角、墙土外摩擦角、地震加速度影响系数等参数对计算结果的影响，再通过与传统拟静力法的计算结果对比，验证本文方法的合理性.

1 理论模型

1.1 计算假定

本文土压力理论模型见图1，计算采用以下基本假定［12－13］:

1)挡土墙为刚性，墙背竖直，填土面水平;

2)墙后填土为各向同性且均质的无粘性土;

3)当填土处于极限平衡状态时，墙背处和滑裂面土体达到应力极限状态;

4)滑动土体有两条滑裂面，一条沿着墙背，另一条位于墙后填土内，滑裂面形状由水平土层的静力平衡方程确定;

5)每个水平土层单元上的应力沿土层长度的变化不大，可由每层对应的墙背处D和滑裂面处E的应力平均值来表示;

6)地震作用按照拟静力法思路，以惯性力的形式施加在水平土体单元层上.

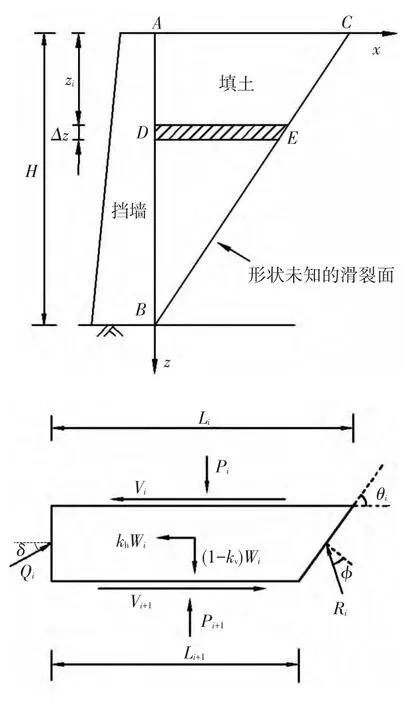
图1 挡土墙地震主动土压力计算模型

1.2 应力分析

在平移模式下，挡土墙的位移达到一定程度时，墙背面和滑裂面的土体达到极限应力状态，由于摩擦力的存在，主应力的方向发生偏转，φ为填土内摩擦角，δ为墙土间外摩擦角，θ为该水平层的滑裂面倾角，墙背处D和滑裂面处E的应力摩尔圆见图2.

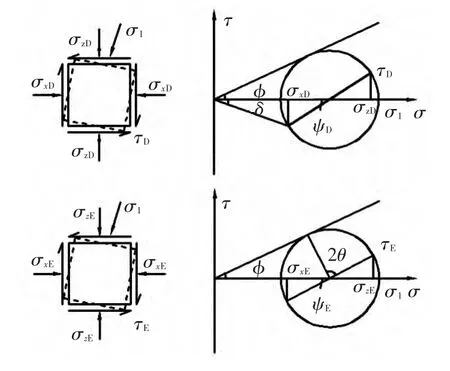
图2 墙背和滑裂面处土体的应力状态

墙背面D点的应力状态:

1)水平应力

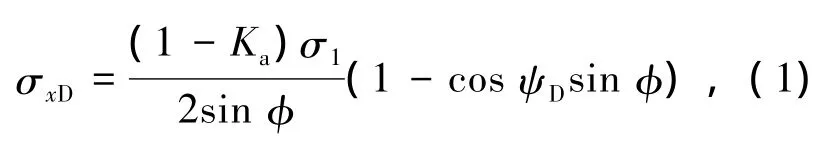
式中σ1为大主应力，Ka为朗肯主动土压力系数，

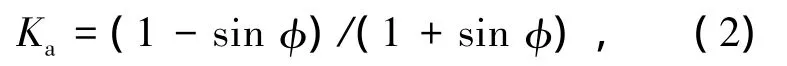
ψD为墙背面处主应力偏转角，

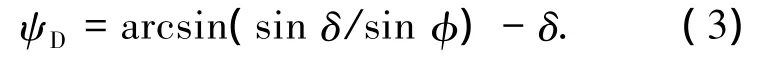
2)剪应力

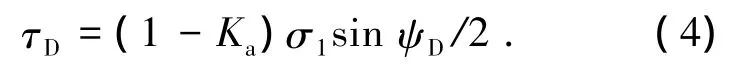
3)竖向应力

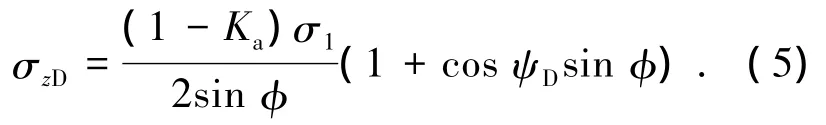
4)墙背面反应力的水平和竖直分量

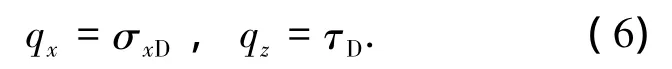
墙后填土中滑裂面E点的应力状态:

1)水平应力

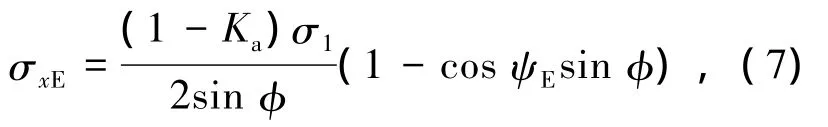
式中ψE为填土中滑裂面处的主应力偏转角，由文献［13］分析可得

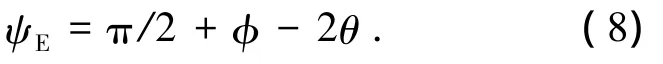
2)剪应力

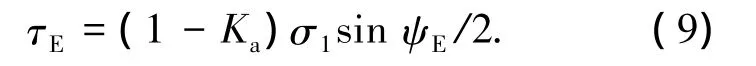
3)竖向应力

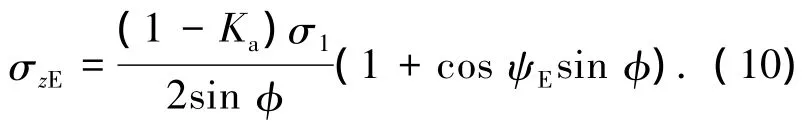
4)滑裂面外法线方向的正应力

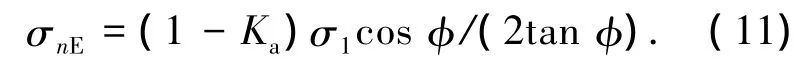
5)平行于滑裂面的切应力

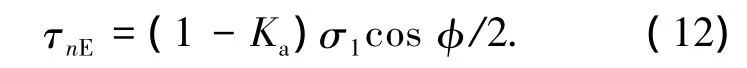
6)滑裂面处反力的水平分量

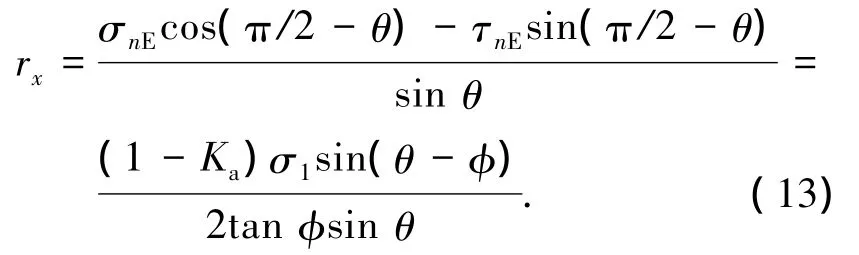
7)滑裂面处反力的竖直分量

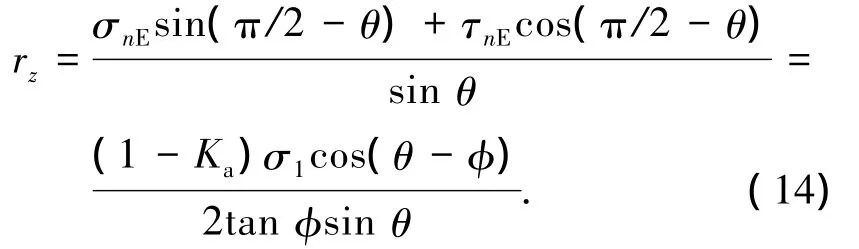
1.3 水平层受力分析

从滑动土体中，任取一水平单元薄层DE，见图1，其上表面长Li，下表面长 Li+1，上表面深度zi，厚度为Δz，作用于水平土层上的力包括:上下表面的竖向应力pi、pi+1和剪力Vi、Vi+1;墙面处反力合力为Qi，其水平和竖向分量Qxi、Qzi;每层的墙面处反力应力的水平和竖向分量qxi、qzi;滑裂面处反力合力为Ri，其水平和竖向分量Rxi、Rzi;每层的滑裂面处反力应力的水平和竖向分量rxi、rzi;水平土层自重Wi，水平和竖向地震惯性力khWi、kvWi，其中，kh、kv分别为水平和竖向地震加速度影响系数.

根据基本假设5)，水平单元土层上的竖向应力和剪应力都用滑动土层两端土体的应力平均值表示，则上下表面的剪力表示为

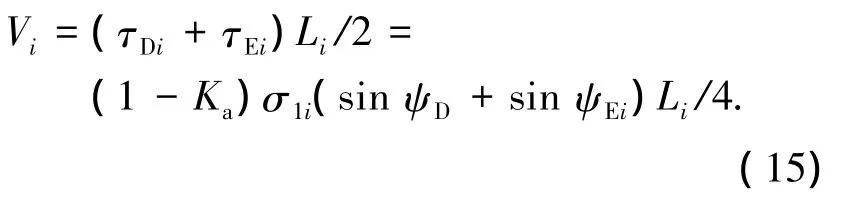
平均竖向应力

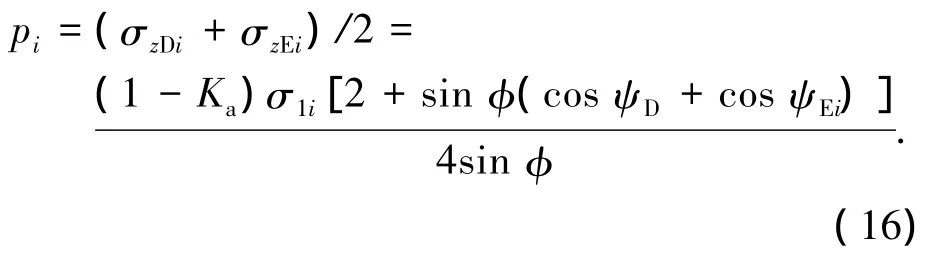
墙背面反力的水平分量

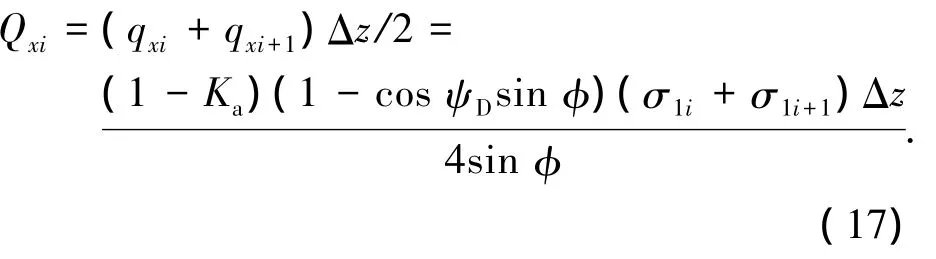
墙背面反力的竖向分量

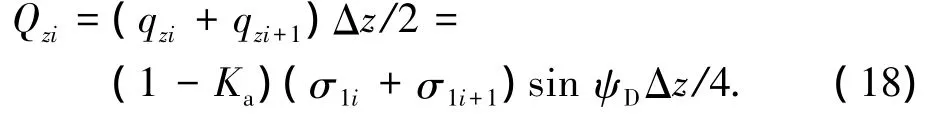
滑裂面反力合力的水平分量，用应力沿着水平层厚度的平均值表示

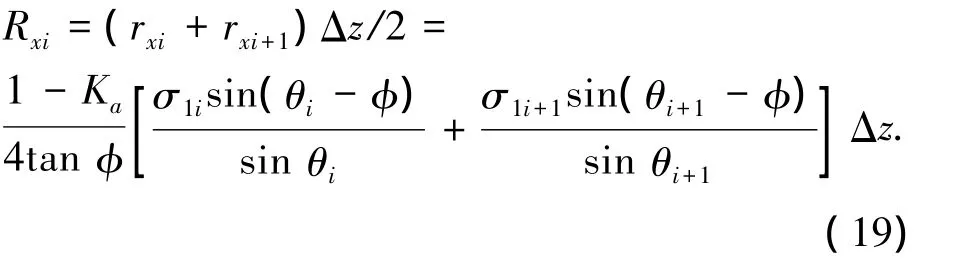
同理，滑裂面反力合力的竖向分量

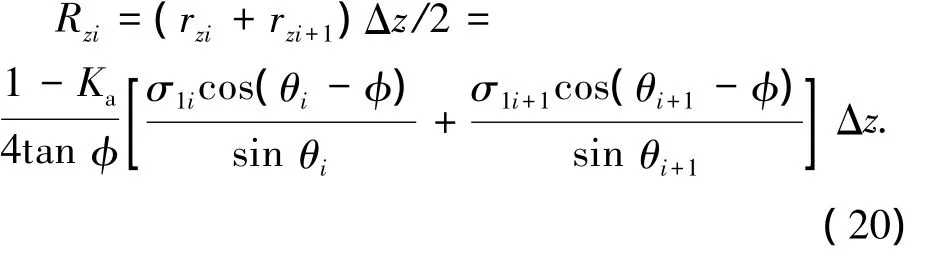
水平单元土层的自重

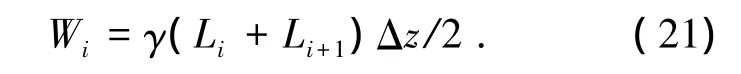
其中γ为土重度，

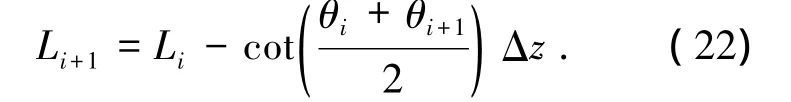
1.4 基本方程和计算方法

水平单元土层DE在各力作用下静力平衡.水平方向上有

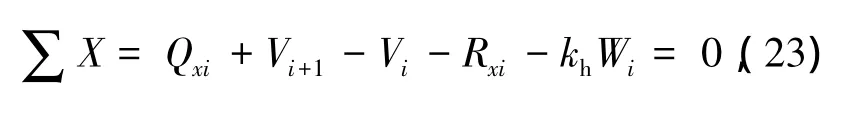
竖直方向上有

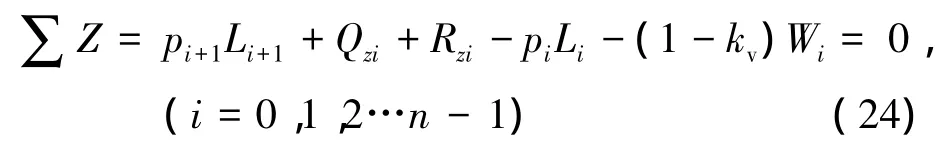
地震主动土压力水平合力可表示为

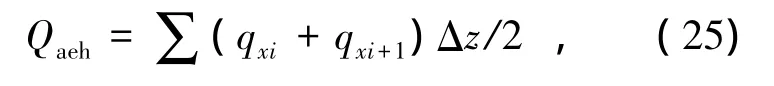
土压力合力为

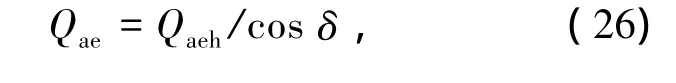
合力作用点可表示为

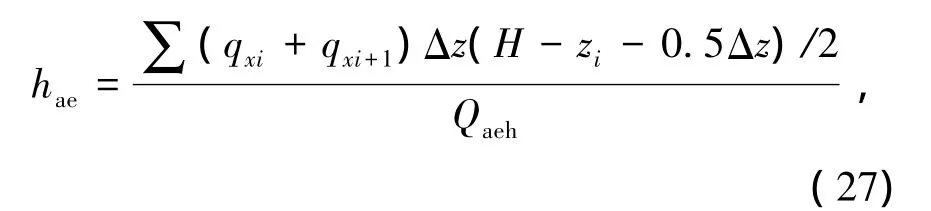
地震主动土压力系数为

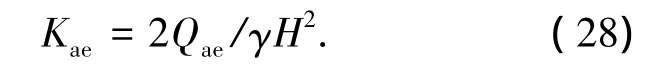
当滑动土体被划分为n个水平单元层时，式(23)、(24)就组成了2n个基本方程，通过整理后，方程组未知量为每个水平单元土层的滑裂面倾角θ0～θn和大主应力σ10～σ1n，共有2n+2个未知量，需要另外补充两个条件方能求解，对于填土的边界面(z=0)处，设墙后填土有均布超载p，必须满足第一个水平单元层的上表面竖向平均应力与超载相等，即p0=p;另外，在水平单元层较薄时，相邻土层的滑裂面倾角变化很小，可近似取θ0= θ1.

由于基本方程组对θ是隐式方程，不能直接求解，本文采用迭代搜索算法编程计算，首先假定填土顶面的水平单元土层长L0和滑裂面倾角θ0(可采用库伦土压力理论所得的滑裂面角为初值)，并由边界面超载p表示出第一水平层的σ10，将σ10代入式(24)表示出σ11，然后把θ0和σ11代入式(23)验证是否满足水平方向平衡条件，若不满足则调整θ0，重复上述步骤直到满足平衡.与第一层类似，每个水平土层采用此算法搜索满足平衡条件的θi，并表示出Li，当逐层计算到滑动土体的底部时，若计算出的Ln≈0，即满足预定的计算精度，则输出计算结果，否则，设定步长调整L0，Ln＞0就减小L0，Ln＜0就增大L0，步长的设置需要反复地试算.重新搜索计算，直到满足精度要求为止.当迭代试算过程收敛时，计算结果一旦满足要求，程序就结束计算，所得的结果在精度范围内是唯一的.最后，将计算结果按照式(25)～(28)可求出主动土压力合力、合力作用点和土压力系数，计算流程见图3.

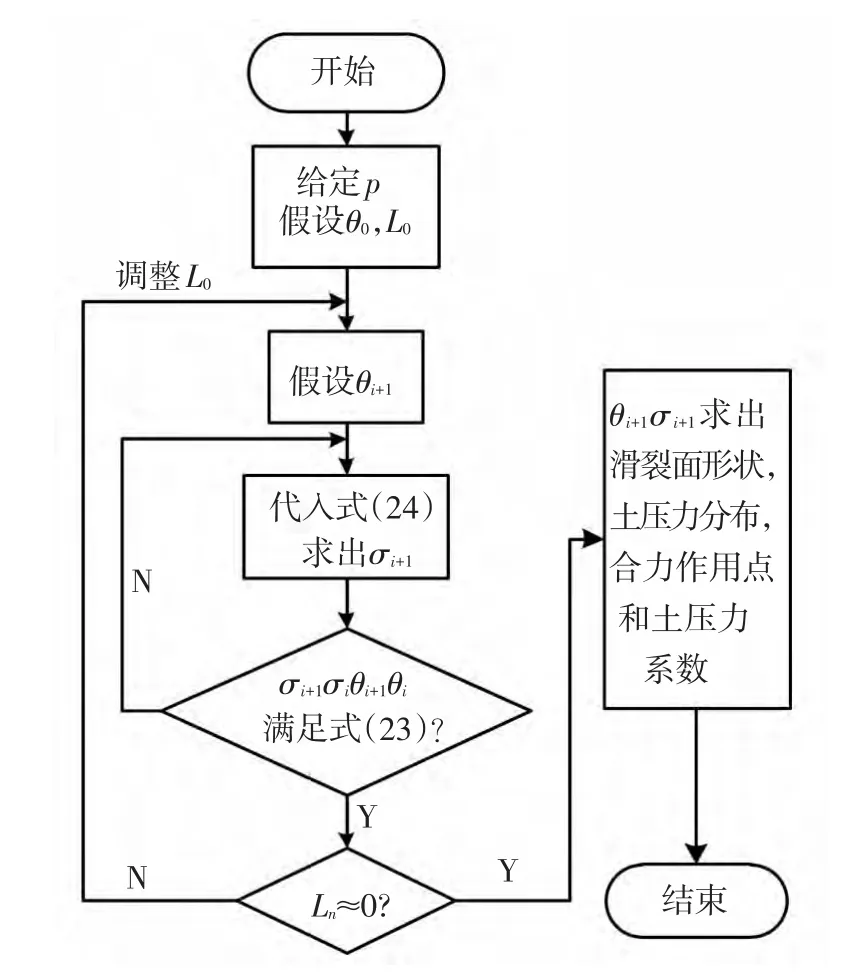
图3 主动土压力的计算流程

2 参数分析

现按照所述的计算思路，对参数进行分析，统一选取土重γ=18 kN/m3，墙高H=10 m，填土面超载p=0，讨论土的内摩擦角φ、墙土外摩擦角δ、水平和竖向地震加速度影响系数kh和kv，对滑裂面、土压力分布、土压力系数及合力作用点的影响.

2.1 滑裂面形状

本文方法并没有预先假设滑裂面的形状，而是根据对每一水平土层的静力平衡，搜索该层对应的倾角值θi，由此得到每个土层的长度Li，从而可绘出滑裂面形状，不同参数所得的滑裂面形状见图 4，工况情况分别为:(a)φ =25°、30°、35°、40°，δ=0.5φ，kh=0.2，kv=0.5kh;(b)φ =40°，δ =0、1/3φ、1/2φ、2/3φ，kh=0.2，kv=0.5kh;(c)φ =40°，δ=0.5φ，kh=0、0.1、0.15、0.2、0.25，kv=0.5kh;(d)φ =40°，δ=0.5φ，kh=0.2，kv=0、1/3kh、1/2kh、2/3kh、kh.

由图4可知，通过搜索绘出的滑裂面形状曲线近似为直线状，对于一般工程计算，地震作用下，假设挡土墙后非粘性土的滑裂面为平面是比较合理的.参数讨论表明，土的内摩擦角φ和水平地震加速度系数kh对滑裂面倾斜角度的影响非常明显，而墙土摩擦角δ和竖向加速度系数kv的影响相对较小.滑裂面相对水平面的总体倾斜角度随着地震加速度的增大而减小，随着内外摩擦角的增大而增大.土拱引起的主应力偏转主要由参数δ体现，计算表明，δ对滑裂面形状的影响主要体现在墙高的中上部，在墙高中部以下，滑裂面形状差别不大.值得注意的是，基于本文假设所得的滑裂面形状，在加速度作用较大或摩擦角较小时，曲线出现了略微反拱，其原因主要是根据静力平衡条件搜索滑裂面倾角时，挡土墙的中上部土层大主应力较小，由大主应力表示的水平剪力也较小，水平向剪力和地震力对土层的影响不如挡土墙下部土层的大，静力平衡时的滑裂面角就出现上面小下面大的情况.

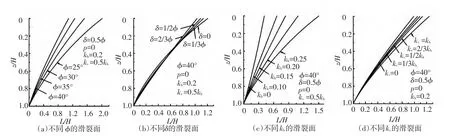
图4 滑裂面形状曲线的参数分析

2.2 土压力分布

按流程图，选取与滑裂面分析时类似的工况，得到的土压力分布见图5.由于不同墙土摩擦角δ时，土压力分布曲线的区分度较小，故图5只给出不同φ、kh、kv时的土压力分布曲线.结果同样表明，土的内摩擦角和水平地震加速度影响系数对土压力分布的影响较为显著，竖向加速度系数影响较小.土压力随着水平和竖向地震加速度影响系数的增大而增大，随着内摩擦角的增大而减小.计算深度在0.8H以内时，土压力的分布近似为线性变化，在0.8H到H范围内，与非地震作用时的土压力先增大后减小变化不同，地震作用下，土压力出现了增大趋势陡增的非线性变化，并且水平地震作用越大，非线性化的陡增趋势越明显，可见，地震会引起土压力的重分布.与文献［10］相比，本文针对平动模式的挡土墙，采用不同的滑裂面假定，并且利用静力平衡条件考虑土拱影响，再加之地震作用，故土压力的分布形式存在较大不同.

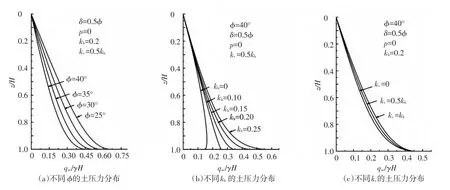
图5 土压力分布曲线的参数分析

2.3 土压力系数和合力作用点

按照式(27)、(28)，求得不同摩擦角和水平地震加速度系数下，地震主动土压力系数Kae和合力作用点hae的结果见表1.相同地震加速度时，Kae随内摩擦角φ的增大和水平地震作用的减小而显著减小，随墙土摩擦角δ的增大而略微减小;与此不同，合力作用点hae对内摩擦角的变化并不敏感，内摩擦角相同时，δ较大，合力作用点略微向上升高;摩擦力情况相同时，作用点随地震作用的增大而下降.

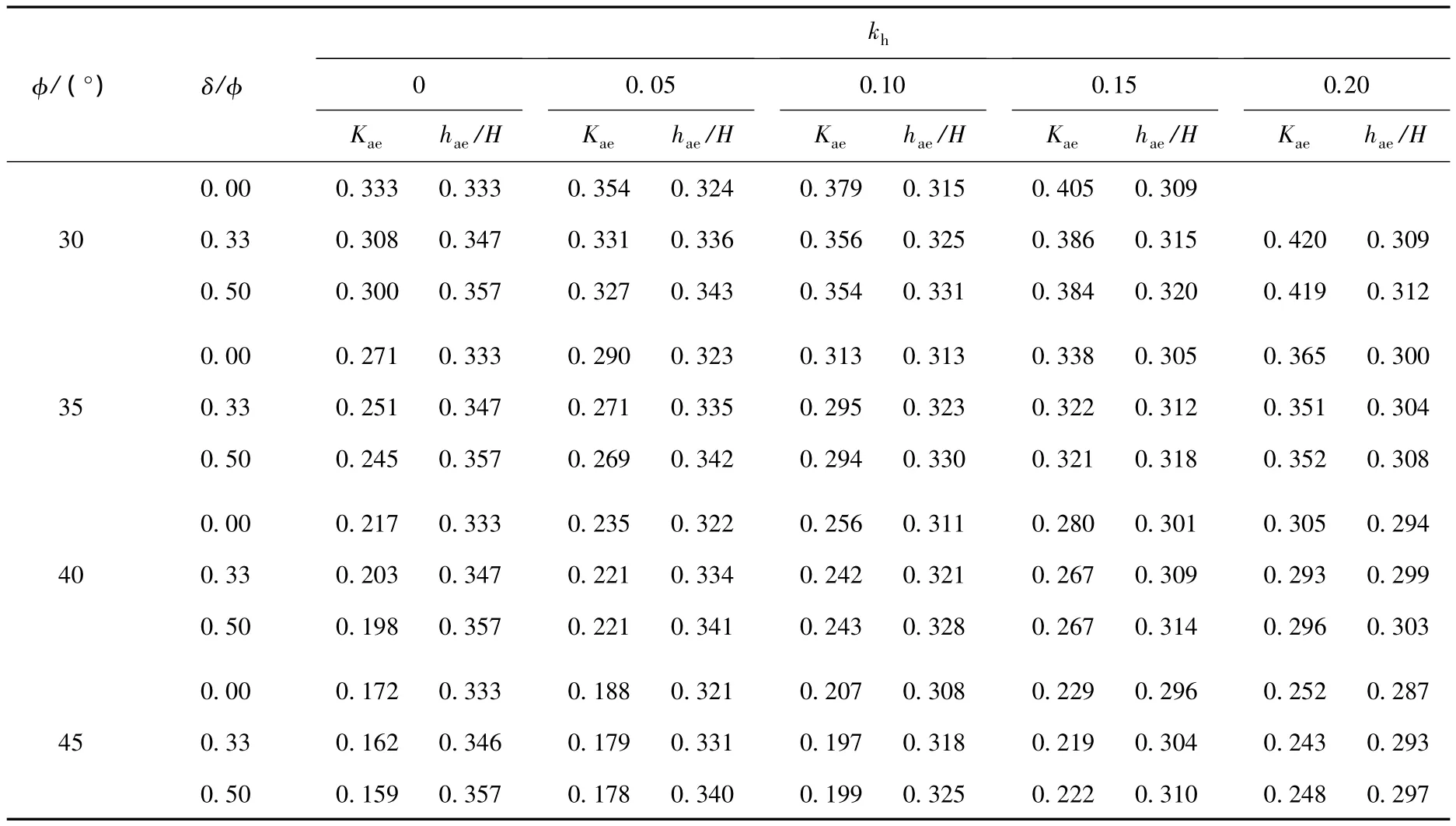
表1 土压力系数和合力作用点

3 理论对比

采用本文方法和传统的Mononobe－Okabe拟静力法计算地震主动土压力的分布，结果对比见图 6，计算参数为 φ =40°，δ=0.5φ，kh=0.2，kv=0.5kh.

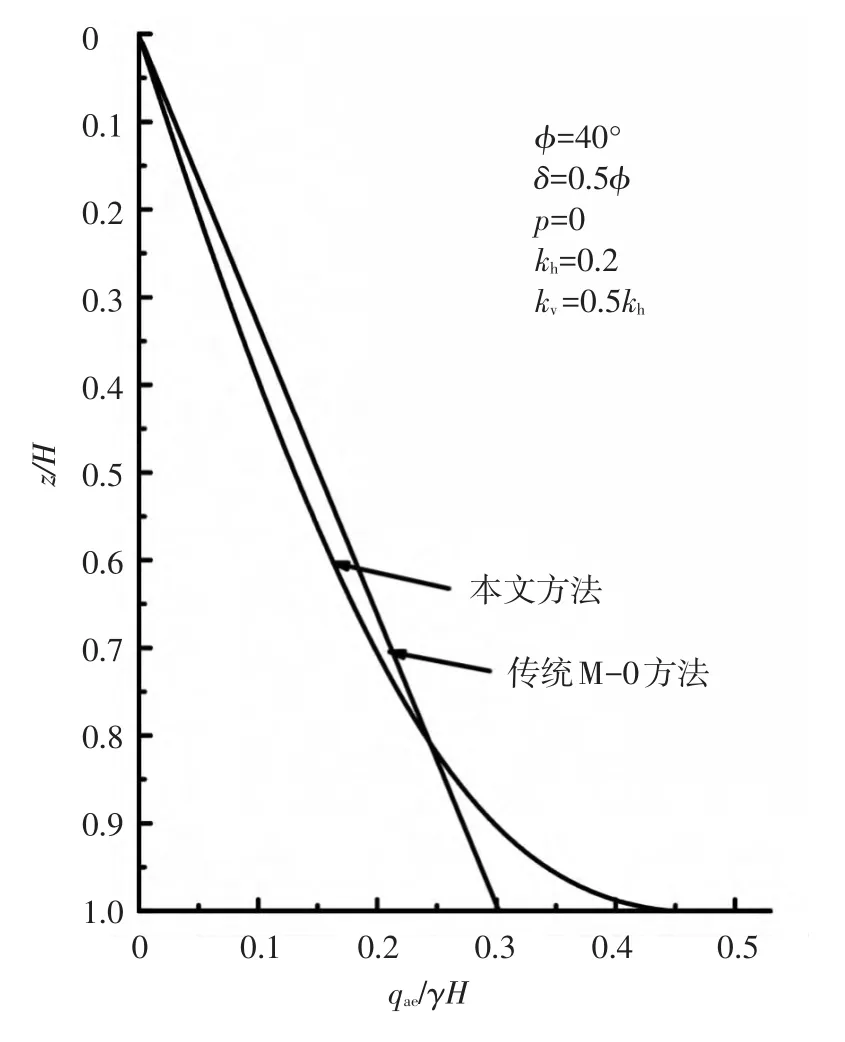
图6 土压力分布曲线对比

由图6可看出，本文方法所得结果和拟静力法整体上基本吻合，但由于传统拟静力法是由库伦土压力理论直接演化而来，土压力分布曲线是由合力计算公式沿深度求导所得，而合力是关于深度的二次函数形式，故曲线为线性变化.本文则是将拟静力的思路结合水平层法计算土压力，同时考虑了土拱效应造成的主应力偏转，所得结果在计算深度0.80H以内与传统拟静力法差别不大，而在0.8H到H段，土压力值非线性增大趋势变强，整个土压力分布为曲线形式.

4 结论

1)基于拟静力法的思路，考虑土拱效应引起的主应力偏转和土层间的剪应力，对平移模式下的挡土墙地震主动土压力的水平层法进行了改进.通过土体的应力分析和水平层的静力平衡条件建立基本方程组，采用编程的方法进行搜索计算，得到极限平衡状态下的滑裂面形状，进而求出土压力分布曲线，土压力系数和合力作用点.

2)对于非粘性土的情况，按照本文方法逐层搜索得到的水平层滑裂面倾角θi，沿深度变化的曲线近乎为直线，故对于工程中的简化计算，假设平面滑裂面是比较合理的.

3)填土内摩擦角和水平地震作用对土压力分布有显著影响，而墙土间摩擦角和竖向地震作用的影响相对较小;土压力系数Kae随着内摩擦角增大和水平地震作用的减小而显著减小;随墙土摩擦角的增大而略微减小;合力作用点高度随内摩擦角变化不大，随墙土摩擦角的增大和地震作用的减小而略微升高.

4)与传统拟静力法计算的地震主动土压力分布相比，本文计算所得结果基本相符，但是土压力曲线呈非线性变化.

［1］WANG Yuanzhan.Distribution of earth pressure on a retaining wall［J］.Geotechnique，2000，50(1):83－88.

［2］王元战，李新国，陈楠楠.挡土墙主动土压力分布与侧压力系数［J］.岩土力学，2005，26(7):1019－1022.

［3］王立强，王元战，迟丽华.挡土墙地震土压力及其分布［J］.中国港湾建设，2007(5):1－5.

［4］杨剑，高玉峰，程永锋，等.地震条件下倾斜挡土墙被动土压力研究［J］.岩土工程学报，2009，31(9):1391－1397.

［5］林宇亮，杨果林，赵炼恒，等.地震动土压力水平层分析法［J］.岩石力学与工程学报，2010，29(12):2581－2591.

［6］NOURI H，JONES C.Development of horizontal slice method for seismic stability analysis of reinforced slopes and walls［J］.Geotextile and Geomembranes，2006，24(3):175－187.

［7］AZAD A，YASROBI S，PAK A.Seismic active pressure distribution history behind rigid retaining walls［J］.Soil Dynamics and Earthquake Engineering，2008，28(5):365－375.

［8］NOURI H，FAKHER A，JONES C.Evaluating the effects of the magnitude and amplification of pseudostatic acceleration on reinforced soil slopes and walls using the limit equilibrium horizontal slices method［J］.Geotextile and Geomembranes，2008，26(3):263－278.

［9］PAIK K H.Estimation of active earth pressure against rigid retaining walls considering arching effects［J］.Geotechnique，2003，53(7):643－653.

［10］应宏伟，蒋波，谢康和.考虑土拱效应的挡土墙主动土压力分布［J］.岩土工程学报，2007，29(5):717－722.

［11］吴明，彭建兵，徐平，等.考虑土拱效应的挡墙后土压力研究［J］.工程力学，2011，28(11):89－95.

［12］章瑞文.挡土墙主动土压力理论研究［D］.杭州:浙江大学，2007.

［13］章瑞文，徐日庆.土拱效应原理求解挡土墙土压力方法的改进 ［J］.岩土力学，2008，29(4):1057－1060.

Improved horizontal slice method for seismic active earth pressure of cohesionless soil

HUANG Rui，XIA Tangdai
(MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering，Zhejiang University，310058 Hangzhou，China)

Based on pseudo-static theory，improved horizontal slice method is derived for retaining walls in translational mode to investigate the influence of principle stress deflection on the earth pressure.The method considers the principle stress deflection of soil behind walls and the horizontal shear force between slices.The basic equations are established according to stress state and static equilibrium condition，and solved by using iterative search algorithm to calculate the slip surface shape，seismic active earth pressure distribution，earth pressure coefficient and resultant force point，then parametric discussion is taken.Numerical results indicate that the slip surface shape for cohesionless soil is approximately linear，so it’s quite reasonable to use the hypothesis of planar slip surface in simplified calculation.In addition，soil friction angle and horizontal seismic action significantly impact earth pressure distribution，instead，the influence of wall friction angle and vertical seismic action are relatively smaller.Compared with the traditional pseudo-static method，earth pressure distributions by two different methods basically agree with each other，but the curve from the improved horizontal slice method trends towards nonlinear increase.

earthquake;earth pressure;horizontal slice method;principle stress deflection

TU432

A

0367－6234(2014)02－0085－07

2013－06－24.

国家自然科学基金与高速铁路基础研究联合基金资助项目(U1234204).

黄 睿(1987—)，男，博士研究生;

夏唐代(1965—)，男，教授，博士生导师.

黄 睿，zjuhr@hotmail.com.

(编辑 赵丽莹)