下穿U型道路在行驶车辆作用下的动力响应

刘 波，张经川，王有志

(山东大学土建与水利学院，250061 济南)

下穿U型道路在行驶车辆作用下的动力响应

刘 波，张经川，王有志

(山东大学土建与水利学院，250061 济南)

为了解下穿U型道路在车辆荷载作用下的动力特性，通过对车辆、下穿U型道路振动系统的分析，将车－路耦合振动问题分解成两个独立的运动体系，即车辆振动子系统和道路振动子系统.利用车轮和路面的位移协调方程来考虑车路的接触，在空间整体车辆模型振动微分方程推导的基础上，考虑路面不平度的三维空间分布，对路面不平度非一致激励下U型道路的动力响应进行研究.结果表明，当路面平顺时，车－路耦合作用力波动很小;随着路况的变差，车－路耦合作用力迅速增大;在路面不平度的非一致激励下，左右轮作用力存在明显差异.车辆行驶速度对动载系数的影响较小，路面不平度对动载系数的影响较大.路况较差时，应考虑车辆荷载的冲击效应.

下穿U型道路;车－路耦合振动;三维路面重构;动载系数

随着我国公路、铁路等基础设施建设的快速发展，公铁立交日益增多，下穿U型钢筋混凝土道路的应用也逐渐增多［1－2］.作为一种较新的结构形式，下穿U型道路一般用于地下水渗透系数较大的含水地层及由于特殊原因不允许降低地下水的路堑.但是目前对于下穿U型钢筋混凝土道路的研究较少，对于车辆荷载作用下的动力响应往往采用经验类比法估算，理论与实际出入较大.因此，对于下穿U型道路尤其是底板在车辆荷载作用下的动力性能进行相关研究、提高U型道路的设计水平迫在眉睫.车辆在混凝土道路上行驶，由于道路路面的不平整或存在病害等，诱发车辆振动，使得车辆荷载作用于道路的竖向力波动变化，而这种波动变化的力会引起路面板的振动和变形，从而会进一步影响车辆的振动.国内外很多学者对车路耦合振动问题进行了相关研究.Hardy等将路面简化为温克尔地基弹性梁，对1/4车辆模型在路面高差激励下的位移响应进行了研究［3］.Cebon D等利用试验和有限元方法对车辆－路面结构的相互作用进行了系统研究［4］.周玉民等建立了1/4车－路耦合动力学模型，将路面结构视为地基梁或地基板，引入动态接触算法，采用直接积分法求解了水泥混凝土路面的动态响应［5］.张峰等基于D’Alembert原理推导了1/2三轴车辆、路面和路基冻结层的振动微分方程，并采用Wilson-θ法对动力方程进行了求解［6］.本文通过对车辆、下穿U型钢筋混凝土道路振动系统的分析，将车－路耦合振动问题分解成两个独立的运动体系，即车辆振动子系统和道路振动子系统，继而利用车轮和路面的位移协调方程来考虑车路的接触.在空间整体车辆模型振动微分方程推导的基础上建立车辆振动模型，采用壳单元建立下穿U型道路初始有限元模型，考虑路面不平度的三维空间分布，编写车路耦合振动分析程序，对路面不平度非一致激励下U型道路的动力响应进行了分析和研究.

1 车－路耦合竖向振动分析模型

1.1 空间整体车辆模型

针对路面不平度的空间分布特性，将汽车悬架、轮胎模拟为线性弹簧和阻尼器，考虑刚性车身的浮沉、俯仰、侧倾3个自由度，建立3轴9自由度空间整车模型，如图1所示.图中M为车体质量，3个自由度分别为竖向位移Z0、绕横轴的旋转自由度θ和绕纵轴的旋转自由度φ;mi为构架质量与轮对质量之和，每个块质量被赋予了一个竖向位移自由度Zi;Kui为二系竖向刚度;Cui为二系竖向阻尼;Kdi为一系竖向刚度;Cdi为一系竖向阻尼.

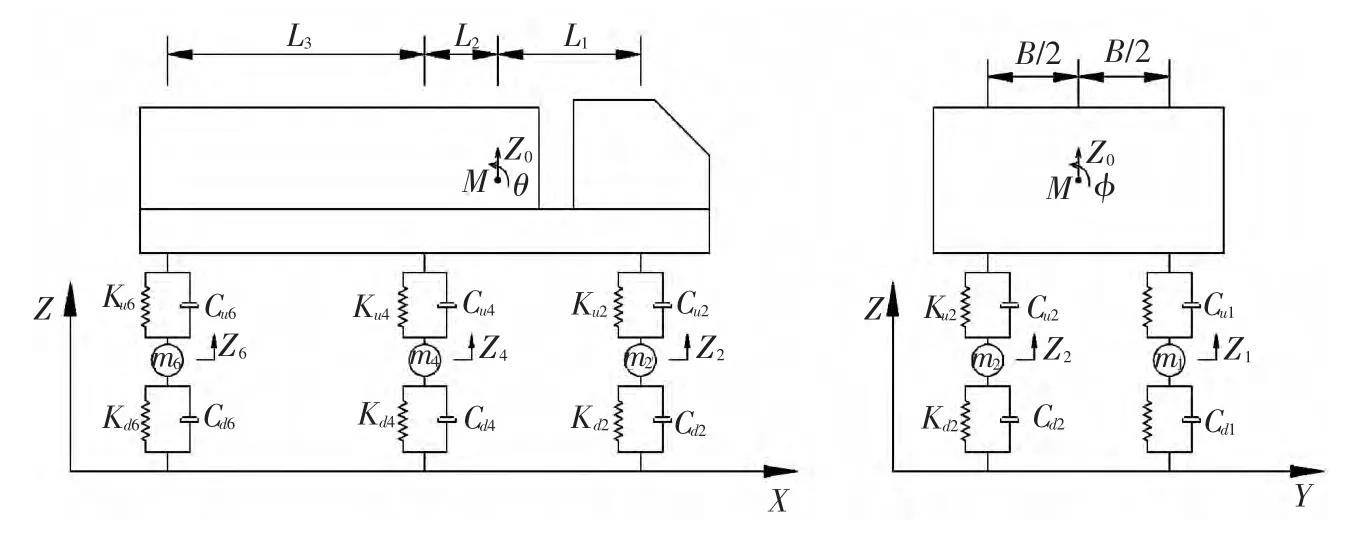
图1 车辆简化模型

以车辆静力平衡位置为起始点，在俯仰角θ和侧倾角φ较小的情况下，车身第i个端点竖向位移方程为

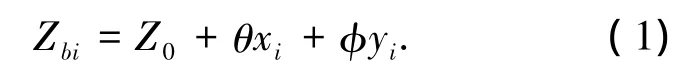
由广义虚功原理得

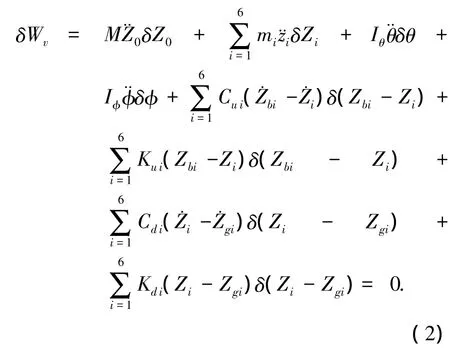
式中:δZ0、δZi、δθ、δφ 均为车辆广义虚位移，不为零，i=1，2，…，6;δZgi为路面广义虚位移，相对车辆而言假设为零.

将式(1)代入式(2)，令广义虚位移对应系数项为零，可得

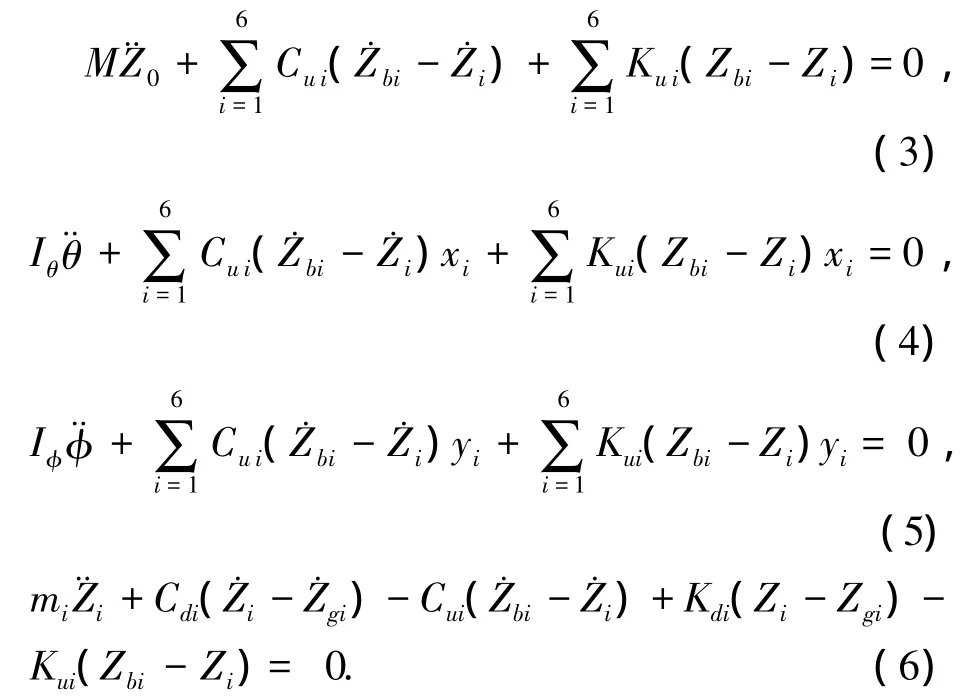
式(3)～(6)分别对应车身质心竖向运动方程、车身俯仰运动方程、车身侧倾运动方程、车轮竖向运动方程;xi、yi表示车轮的平面坐标.

将上述各式整理写成矩阵形式得

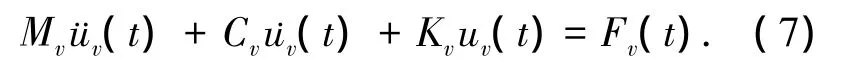
1.2 下穿 U 型道路模型［7－8］

假定路面为温克尔地基上各向同性弹性薄板，其竖向运动方程为

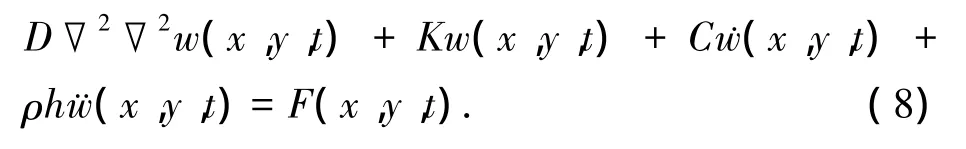
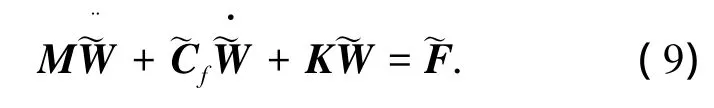
1.3 位移协调条件

假设车轮在运行的过程中始终与路面密贴不脱离，即得车－路耦合振动系统的位移协调条件为

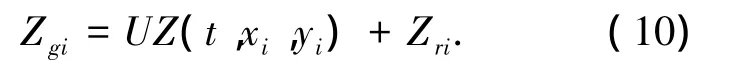
式中:UZ(t，xi，yi)表示车轮i对应路面节点的挠度，向下为负;Zri表示路面上点的不平整度，向下为负.

根据车辆与路面接触点间相互作用力的平衡关系，可得第i个车轮对路面的作用力为

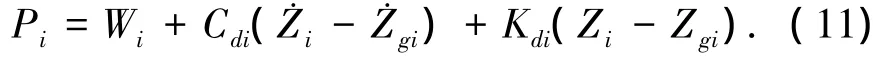
式中:Wi表示车辆静止时车体分配到第i个车轮的重力与该轮自重之和，向下为负.

1.4 车－路耦合振动模型数值求解

本文分别采用Newmark-β隐式积分法进行求解，具体步骤如下:1)建立U型道路弹性地基模型，形成道路子系统质量矩阵、刚度矩阵、阻尼矩阵;2)输入车辆参数，形成车辆子系统质量矩阵、刚度矩阵、阻尼矩阵;3)假定车路耦合振动系统的初始状态;4)根据道路子系统的位移、速度及路面不平整度确定道路子系统对车辆子系统的反作用力，形成荷载向量;5)利用Newmark-β数值迭代法求解车辆子系统振动微分方程组，求出车辆子系统位移向量、速度向量、加速度向量;6)计算车辆子系统对道路子系统的作用力，求解道路子系统振动微分方程组;7)判断平衡迭代收敛情况，若满足收敛条件，则停止迭代.

2 路面不平度的三维空间重构

路面不平顺是引起车辆对路面的动力响应的主要激励因素，目前通常用功率谱密度来描述路面的不平度［9－10］，车辆振动输入－路面平度表示方法中，建议路面功率谱密度为

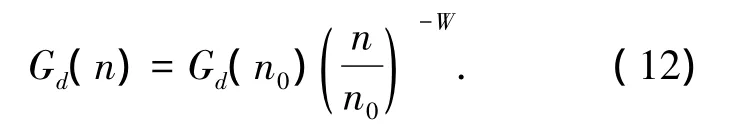
式中:Gd(n0)为路面平度系数;n为空间频率;n0为参考空间频率，n0=0.1 m-1;W为频率指数，通常取2.

在对道路进行平整度模拟时，多采用谐波叠加法对沿道路长度方向路面不平度进行重构，即

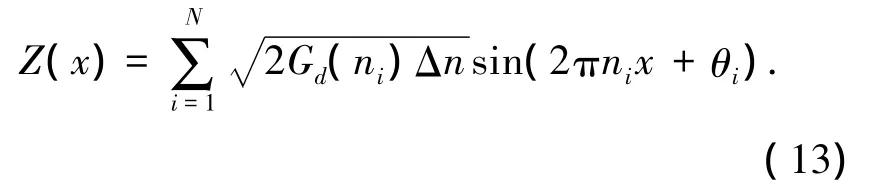
式中:x为路面的纵向位置;θi∈［0，2π］，为随机相位;N为充分大的整数;Δn=(nu-nl)/N;nl、nu分别为空间频率的上下限.

为将式(13)推至三维空间，令x表示空间点到初始点的距离［11］，则式(13)可表示为

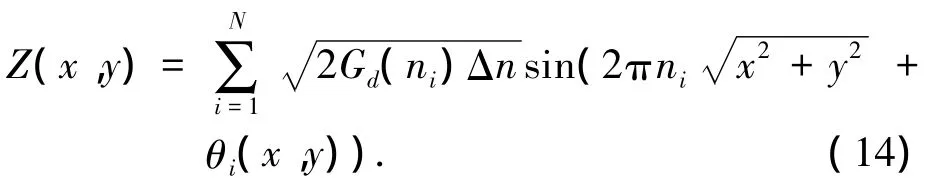
取0.011 m－1＜n ＜ 2.83 m－1，划分为 250 份，采样间隔为0.1 m，根据式(14)可得到3 m×100 m A级路面三维空间路面不平度，如图2所示.

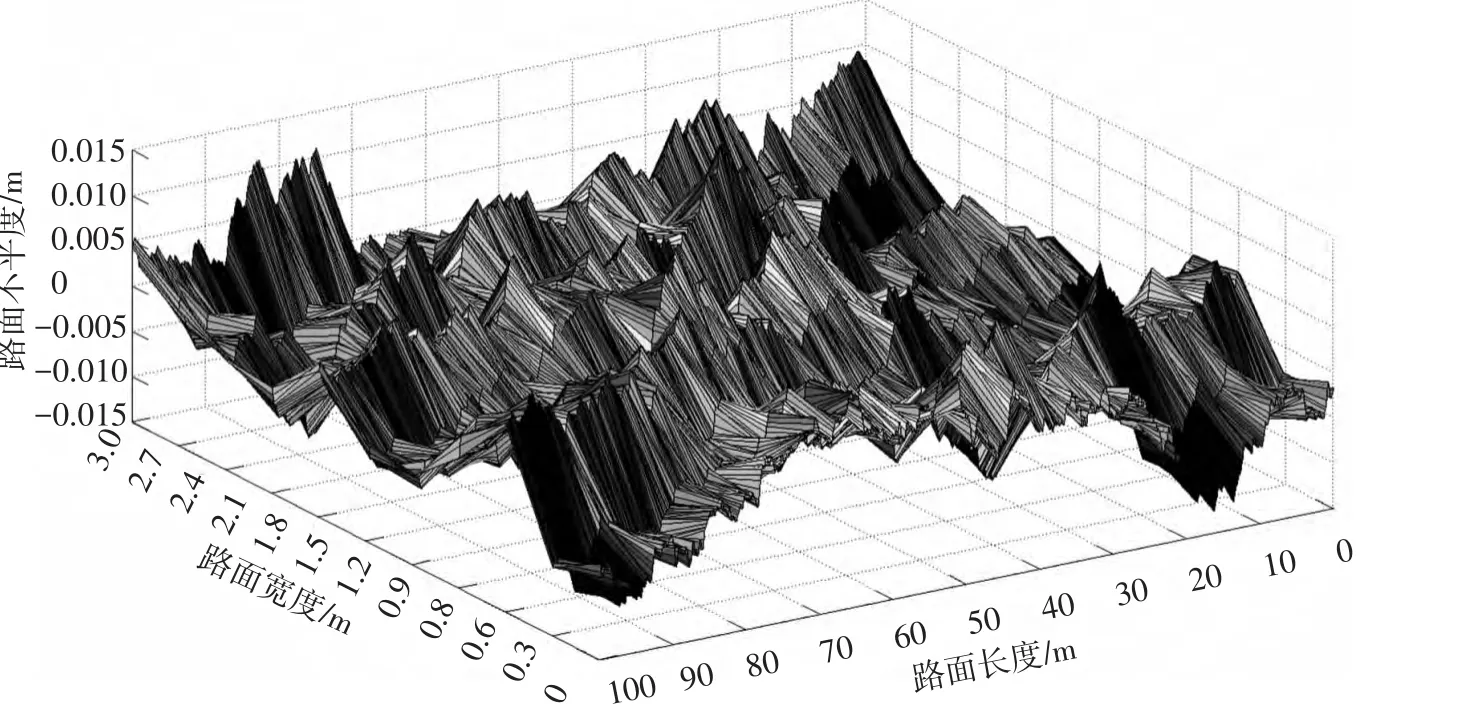
图2 三维A级路面不平度

仿真生成的路面不平度功率谱与标准功率谱必定存在差异，为考察仿真的可信度，选取Y=1.5 m处的X方向路面不平度如图3所示，并采用基于AR模型的现代功率谱估计得到Y=1.5 m处路面不平度功率谱如图4所示.图中虚线表示各路面平度等级标准功率谱的上、下限.从图中可以看出，n∈［0.011，2.83］时，仿真功率谱处于A级路面的上限和下限范围之内，与标准功率谱拟合度较好，说明采用式(14)可以较好地对三维路面不平度进行模拟.

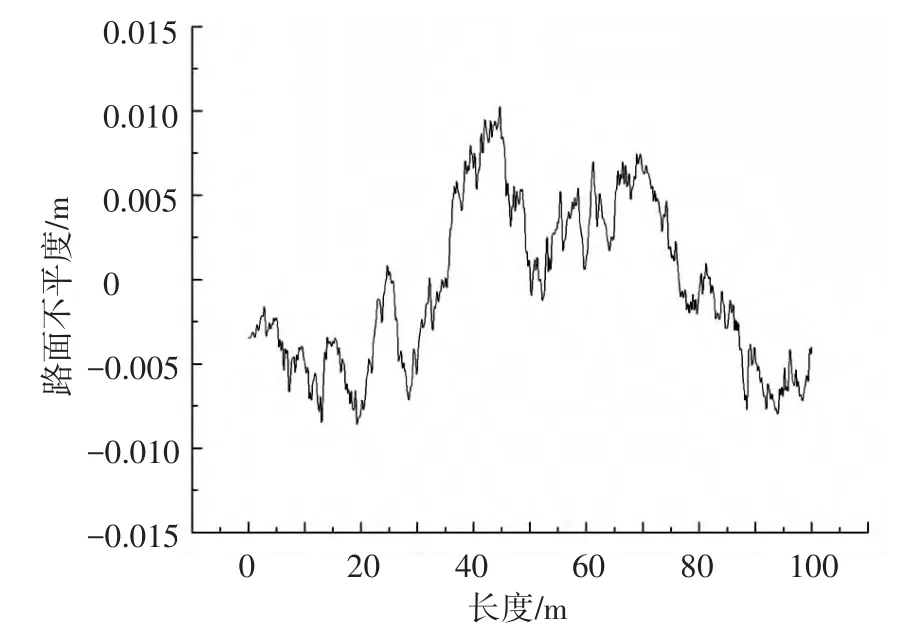
图3 Y=1.5 m处路面不平度

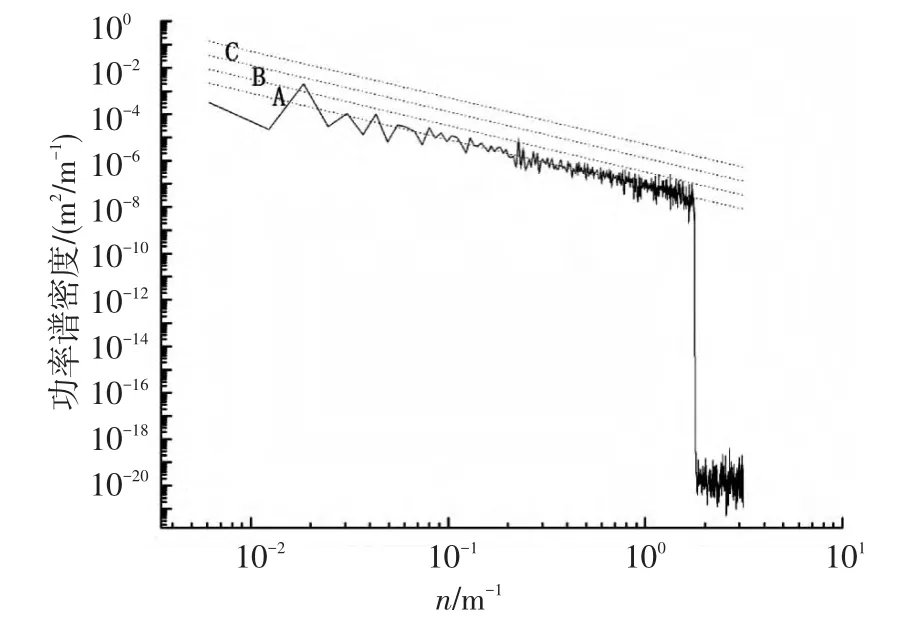
图4 Y=1.5 m处路面不平度功率谱

3 车－路耦合动力响应及结果讨论

3.1 模型计算参数

本文下穿U型钢筋混凝土道路整体断面如图5所示，边墙和底板采用板单元SHELL63进行离散，温克尔地基弹簧采用COMBIN7进行模拟，采用m法考虑边墙土层水平抗力的变化.考虑到下穿U型道路主要修建在城区范围，文中以城市主干道Ⅰ级为例，取标准行车速度为60 km/h.

采用数值积分来研究路面的动力响应时，可得车辆模型、道路模型的相关参数.车体质量M为43 140 kg;车体俯仰转动惯量Iθ为53 700 kg/m2;车体侧倾转动惯量Iφ为13 400 kg/m2;前轴轮胎质量m1～m2为335 kg;前轴悬架刚度 Ku为900 kN/m;前轴轮胎刚度Kd为2 100 kN/m;前轴悬架阻尼系数Cu为4 kN·s/m;前轴轮胎阻尼系数Cd为5 kN·s/m;中、后轴轮胎质量m3～m6为670 kg;中、后轴悬架刚度Ku为1 800 kN/m;中、后轴轮胎刚度Kd为4 200 kN/m;中、后轴悬架阻尼系数Cu为8 kN·s/m;中、后轴轮胎阻尼系数Cd为 10 kN·s/m;路面弹性模量 E为 3.6×1010Pa;路面密度ρ为2 500 kg/m3;地基反应模量K为60 000 kN/m3;地基阻尼系数 C为100 kN·s/m2;水平抗力系数的比例系数 m为5 000 kN/m4.

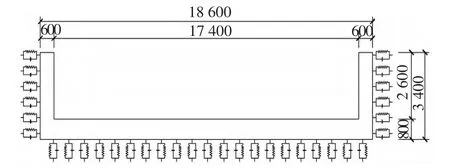
图5 下穿U型道路横断面(mm)

3.2 车－路耦合作用力

车辆以一定速度在混凝土路面上行驶时，车－路耦合作用力为时间和空间的函数.图6为车辆以60 km/h的速度行驶在U型道路上时车辆前轴车轮对路面的动态作用力.可以看出，当路面平顺时，车－路耦合作用力波动很小，根据式(11)可知车辆荷载作用下道路底板的位移和速度均比较小，这与实际情况相符;随着路况的变差，车路耦合作用力迅速增大;同时，左右轮的作用力存在明显差异，这反映出路面不平度的三维分布特性.

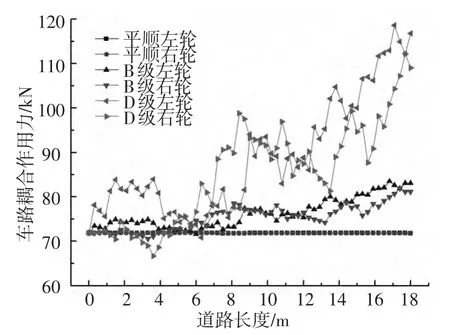
图6 车－路耦合作用力时程曲线

3.3 车辆动力响应

图7～9为当车辆以60 km/h的速度行驶在B级路面上时车体的竖向平动位移Z0、速度Z0'、加速度Z0″时程曲线.从图中可以看出，车体的竖向位移随时间波动变化，受路面不平度的影响，车体竖向位移均大于零，竖向位移最大值为0.013 9 m;车体竖向速度和加速度围绕零值波动变化，其绝对值最大分别达到0.049 3 m/s、0.875 m/s2.

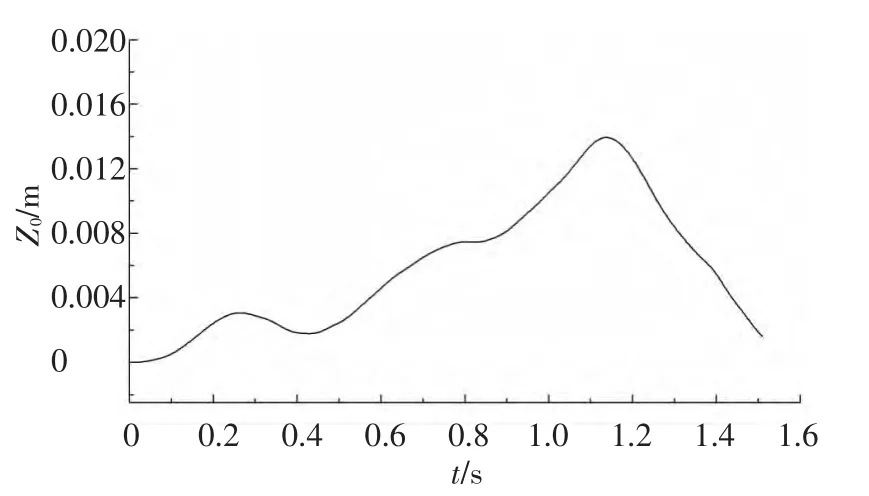
图7 车体竖向位移时程曲线

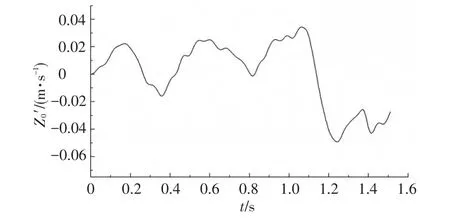
图8 车体竖向速度时程曲线

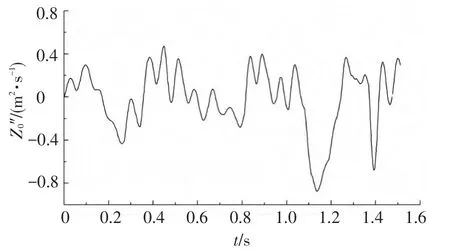
图9 车体竖向加速度时程曲线

3.4 U型道路动力响应

图10、11分别为车辆荷载以60 km/h的速度行驶在B级路面上时U型道路节点的弯沉、弯矩时程曲线，底板弯沉最大值为0.108 mm，弯矩最大值为8.299 kN·m.从图中可以看出，弯矩时程曲线有3个主要波峰，分别对应3个车轴，而弯沉时程曲线则只有1个明显的波峰，对应车辆的中轴，两者的时程曲线变化趋势并非一致.

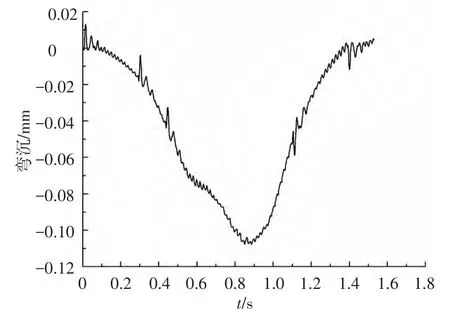
图10 弯沉时程曲线

3.5 车辆荷载的冲击效应

借鉴文献［12］中桥梁冲击系数的定义，定义动载系数为

式中:Adyn为车辆荷载通过时的动力响应峰值;Ast为同一车辆荷载作用时的静力响应值.

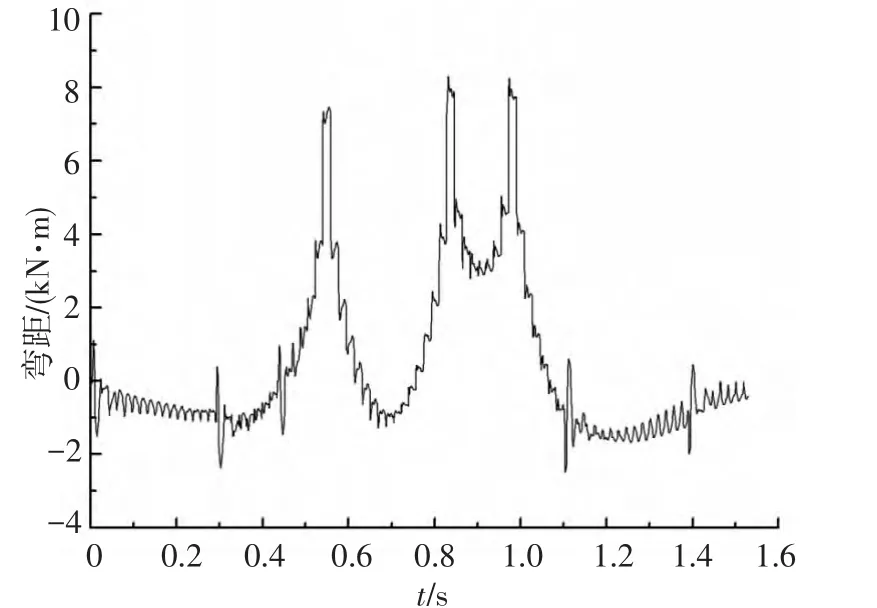
图11 弯矩时程曲线

图12、13分别为不同车速、不同路面平度等级情况下道路的弯沉、弯矩动载系数.可以看出，车辆行驶速度对动载系数的影响较小，路面平度对动载系数的影响较大.以弯矩动载系数为例，路面平顺时，动载系数为1.07～1.10，路面平度等级为A、B、C、D时，其动载系数分别为 1.09～1.13、1.13 ～ 1.15、1.20 ～ 1.23、1.37 ～ 1.41.因此，当路况较差时，应考虑车辆荷载的冲击效应.

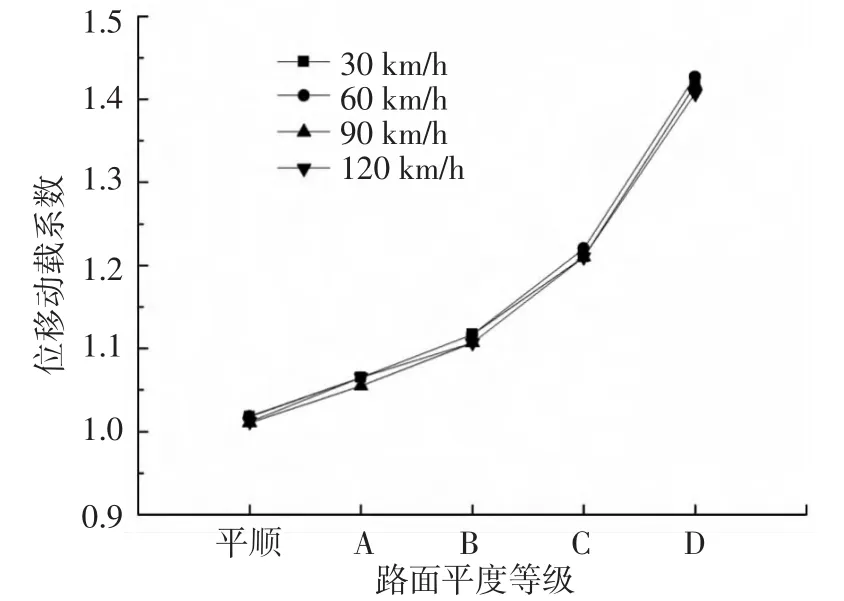
图12 弯沉动载系数

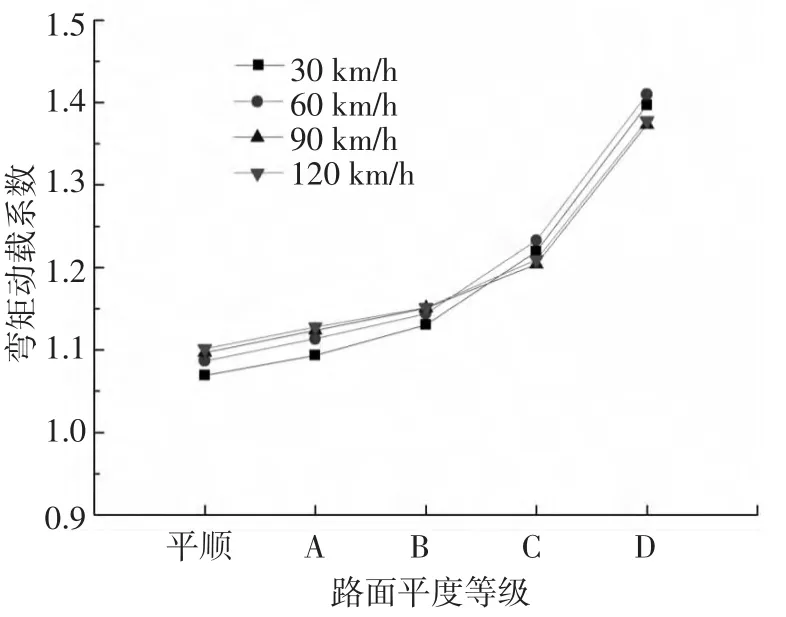
图13 弯矩动载系数

3.6 坑槽与凸起对道路的冲击效应

为进一步研究路面不平度对于道路的冲击效应，对混凝土路面经常存在的坑槽和凸起等病害进行了分析，结果如图14所示.从图中可以看出，车辆行驶到坑槽处时，弯沉突然变小，行驶到凸起处时，弯沉突然变大.

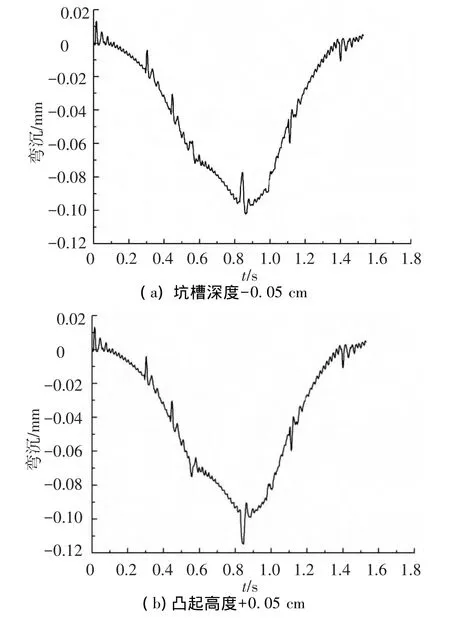
图14 坑槽与凸起路面弯沉对比图

图15为冲击效应，对于路面弯沉(位移)，无坑槽、凸起时动载系数最小;存在坑槽、凸起时，动载系数均大于1.0;绝对值相同，凸起引起的冲击系数较大.对于道路弯矩，路面病害为坑槽时，动载系数小于1.0;路面病害为凸起时，动载系数大于1.0，凸起为0.1 m时，弯矩动载系数达2.09.

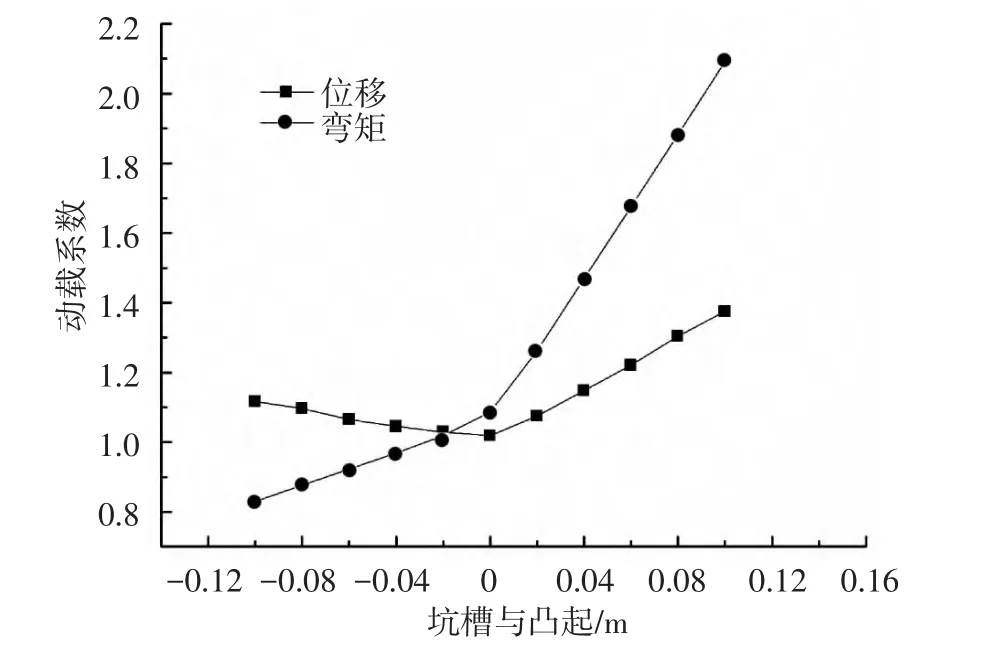
图15 坑槽与凸起引起的冲击效应

4 结 论

1)基于车－路耦合竖向振动的分析模型通过车轮和路面的位移协调方程将车辆振动子系统和道路振动子系统联系起来并进行数值求解，可以准确地分析U型道路的竖向动力响应.采用谐波叠加法可以实现三维空间下路面不平度的重构，仿真功率谱与标准功率谱拟合度较好.

2)当路面平顺时，车－路耦合作用力波动很小;随着路况的变差，车－路耦合作用力迅速增大;在路面不平度的非一致激励下，左右轮作用力存在明显差异.

3)车辆行驶速度对动载系数的影响较小，路面不平度对动载系数的影响较大.路况较差时，应考虑车辆荷载的冲击效应.

4)路面病害为坑槽时，弯沉动载系数大于1.0，弯矩动载系数小于1.0;路面病害为凸起时，弯沉和弯矩动载系数均大于1.0;相同的病害深度(高度)，凸起引起的冲击效应较大.

［1］孟美丽，高海彬.封闭式路堑U形槽结构的设计和计算［J］.铁道建筑，2011(8):81－83.

［2］李虹.公路U形封闭式路堑优化设计方法探讨［J］.铁道标准设计，2011(9):27－29.

［3］HARDY M S A，CEBON D.Response of continuous pavements to moving dynamic load［J］.Journal of Engineering Mechanics，1993，119(9):1762－1780.

［4］CEBON D.Handbook of vehicle-road interaction［M］.Lisse:Swets ＆ Zeitlinger Publishers，1999.

［5］周玉民，谈至明，刘伯莹.1/4车－路耦合动力学模型研究［J］.同济大学学报:自然科学版，2012，40(3):408－413.

［6］张峰，冯德成，凌贤长，等.春融期重载车辆－路面－路基垂向动力分析模型［J］.中国公路学报，2011，24(4):7－14.

［7］SUN L.Dynamic displacement response of beam-type structures to moving line loads［J］.International Journal of Solids and Structures，2001，38(48/49):8869－8878.

［8］KIM S M，MCCULLOUGH B F.Dynamic response of plate on viscous winkler foundation to moving loads of varying amplitude［J］.Engineering Structures，2003，25(9):1179－1188.

［9］DODDS C J，ROBSON J D.The description of road surface roughness［J］.Journal of Sound and Vibration，1973，31(2):175－183.

［10］AU F T K，CHENG Y S，CHEUNG Y K.Effects of random road surface roughness and long-term deflection of prestressed concrete girder and cable-stayed bridges on impact due to moving vehicles［J］.Computers and Structures，2001，79(8):853－872.

［11］吴参，王维锐，陈颖，等.三维路面谱的仿真建模与验证［J］.浙江大学学报:工学版，2009，43(10):1935－1938.

［12］KIM C W，KAWATANI M，KWON Y R.Impact coefficient of reinforced concrete slab on a steel girder bridge［J］.Engineering Structures，2007，29(4):576 －590.

Dynamic responses of U-type road under moving vehicles

LIU Bo，ZHANG Jingchuan，WANG Youzhi

(School of Civil Engineering，Shandong University，250061 Jinan，China)

To analyze the dynamic characteristics of U-type road under moving vehicles，the coupled vibration problem is decomposed into two independent motion system，i.e.vehicle vibration subsystem and road vibration subsystem.The displacement coordination equation of wheel and pavement is used to consider the contact of vehicle and road.Based on the formula derivation of vehicle vibration differential equation，the dynamic responses of U-type road is analyzed and studied with the 3-D spatial distribution of road surface roughness considered.The results show that the fluctuation of vehicle-road coupling force is small when the road surface is smooth.The vehicle-road coupling force increases rapidly with the deterioration of road conditions.The forces of left wheel and right wheel is different under the non-uniform excitation of road surface roughness.Vehicle speed has little effect on the dynamic load coefficient comparing with road surface roughness.The impact of vehicle load should be considered under poor road conditions.

U-type road;vehicle-road coupling vibration;3-D pavement reconstruction;dynamic load coefficient

U416

A

0367－6234(2014)02－0109－06

2013－03－08.

国家自然科学基金资助项目(50779032).

刘 波(1980—)，男，工程师，博士研究生;

王有志(1964—)，男，教授，博士生导师.

王有志，wangyouzhi@sdu.edu.cn.

(编辑 魏希柱)