预测砌体墙板破坏荷载的广义应变能密度方法
黄艳霞,张 瑀,刘传卿,周广春
(1.哈尔滨工业大学土木工程学院结构工程灾变与控制教育部重点实验室,150090 哈尔滨;2.山东省建筑科学研究院,250031 济南)
预测砌体墙板破坏荷载的广义应变能密度方法
黄艳霞1,张 瑀1,刘传卿2,周广春1
(1.哈尔滨工业大学土木工程学院结构工程灾变与控制教育部重点实验室,150090 哈尔滨;2.山东省建筑科学研究院,250031 济南)
为了揭示新板与基础板破坏荷载之间的关系,从面外均布荷载作用下砌体墙板的有限元模型中提取各单元的应变能密度,给出墙板的广义应变能密度概念.通过分析新板与基础板的广义应变能密度分布模式,提出了基于广义应变能密度预测砌体墙板破坏荷载的方法.算例分析表明,本文发展的方法与有限元的分析方法相比,虽然预测精度接近,但该方法具有建模过程简单、不受材料性质参数影响的优点;与屈服线方法相比,预测精度有较大提高.该方法能直接应用现有的试验数据或记录来预测新板的破坏荷载,为砌体墙板破坏荷载的预测提供一个新途径.
砌体墙板;广义应变能密度;破坏荷载;屈服线方法;有限元方法
在砌体结构理论研究方面,我国取得了很多成果,但是砌体结构在风(尤其是台风)、洪水、爆炸荷载等面外水平荷载作用下引起砌体结构损坏和倒塌的研究较少,致使砌体结构设计和施工在抗风、抗洪水冲击、抗爆等方面,缺少有关破坏机理的参考性研究成果.
风荷载、爆炸冲击荷载等可以理想化为面外均布荷载,而对面外均布荷载作用下砌体墙板的破坏模式和破坏荷载预测,较为普遍应用的分析方法有屈服线方法[1]、有限元方法等[2-4].屈服线方法是一种预测砌体墙板破坏强度的方法,其计算结果往往偏于保守,而且由于砌体墙板的脆性性质并不能体现出明显的屈服特性,所以该方法的理论基础通常认为是不合理的[5].有限元方法的计算精度在很大程度上受模型中各种参数的影响,所以对于性质变异明显的砌体结构而言,在许多情况下也是失效的[2,6].对砌体墙板性能影响最大的两个因素是墙板的边界条件及砌体材料自身的变异性[7].有限元方法在某些情况下不能精确模拟砌体墙板的工作行为,是由于砌体的变异性,特别是变异性与边界条件的关系很难合理模拟出来.
Zhou等[8-9]建立了直接基于已知试验墙板的破坏模式来预测未知墙板破坏模式的方法.本文在文献[8]基础上,提出了广义应变能密度概念,并基于相应的广义应变能密度模式,建立预测面外均布荷载作用下砌体墙板破坏荷载的方法.该方法不需对已有试验数据或记录做任何处理,即可直接用来预测未知墙板的破坏荷载.此外,该方法在建立墙板的有限元模型时仅需输入墙板的约束形式和尺寸这两个构造参数,不涉及各种材料参数的输入,大大简化了建模过程.
1 基本概念
基础板:已有试验记录的已知砌体墙板,是预测新板工作性能或工作行为的基础,故统称为基础墙板,简称基础板.
新板:待分析的墙板统称为新板.新板假设其工作性能或工作行为是未知的.为了验证方法并比较预测结果,选择已知试验结果的墙板作为新板.
2 广义应变能密度(GSED)
结构发生破坏的原因通常是其承受的荷载超出了其极限承载力或是其变形超出了极限变形.结构的应力和应变从微观上反映结构的受力状态,于是,本文在结构应力和应变的基础上寻求一个物理参数来确定结构的破坏荷载.因此,应变能密度这个与应力应变同时相关的参数被用来预测砌体墙板的破坏荷载.
砌体作为一种高脆性的材料,一般认为其破坏前是线弹性状态.普通的六面体单元在线弹性阶段的应变能密度计算公式为

而本文提出的广义应变能密度是将单位均布荷载作用下各单元的应变能密度归一化,得到无量纲的值,如式(2)所示.
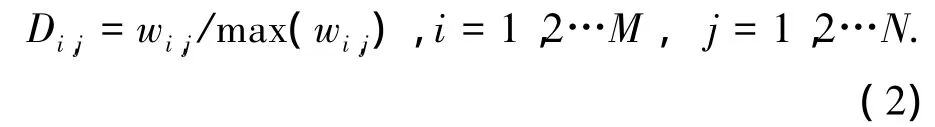
式中:wi,j是单元(i,j)在单位均布荷载作用下的应变能密度;Di,j是单元(i,j)的广义应变能密度;M、N分别是砌体墙板划分单元行列数.
3 广义应变能密度预测砌体墙板破坏荷载的方法
3.1 计算推导
广义应变能密度并不是实际荷载作用下各单元真实的应变能密度,而是在均布荷载作用下,应变能密度的分布模式,反应的是墙板整体特征,于是本文定义各单元的广义应变能密度和值为墙板的整体模式参数k,即
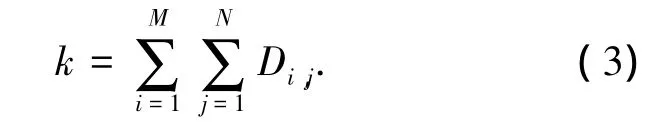
结构的承载能力与其受力状态密切相关,基于结构的受力状态建立破坏准则如下:
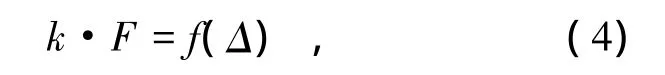
式中Δ是广义位移,f表示由广义位移控制的破坏准则.因为砌体是一种脆性材料,可以认为砌体墙板的破坏过程是线弹性的,故归一化的模式参数k为常数,所以式(4)可写成

因此基础墙板与新板的破坏荷载可分别用式(6),(7)表示:

由于新板和基础墙板遵循统一的破坏准则f(Δ),于是有

式中:kbase,knew分别是基础板和新板的整体模式参数;Fbase,Fnew分别是基础板和新板的破坏荷载.
3.2 计算方法
基于广义应变能密度预测砌体墙板破坏荷载的方法:
1)分别利用有限元方法计算出新板和基础板在单位均布荷载作用下的应变能密度,该方法要求基础板和新板的各单元尺寸基本相同;
2)根据式(2)分别计算出新板和基础板各单元广义应变能密度;
3)按式(3)分别计算出新板和基础板的整体模式参数knew和kbase;
4)按式(8)计算新板的破坏荷载.
4 算例分析
墙板与梁柱,墙板与墙板之间的相互作用即为墙板的边界约束,通常限制墙板的位移,并视限制位移的情况简化为固定约束、简支约束和自由边界.例如,置于槽型钢中的墙板底边可视为固定约束;而由钢柱限制墙板竖直两边垂直于墙面位移的情况,视为简支约束;显然,没有任何位移限制的墙板边缘即为自由边.
常见砌体墙板根据其约束类型可分为:
1)顶边自由,其余三边约束;
2)四边约束;
3)两对边自由,其余两边约束;
4)一边约束,其余三边自由.
本文分别对前两类常见约束形式的砌体墙板的破坏荷载进行预测.
对于顶边自由、其余三边约束的板,本文以Chong的试验数据[3],不同厚度的实心砌体墙板在面外均布荷载作用下的试验结果为算例(见表1),分别与屈服线方法及有限元方法进行比较,来验证本文方法的有效性.
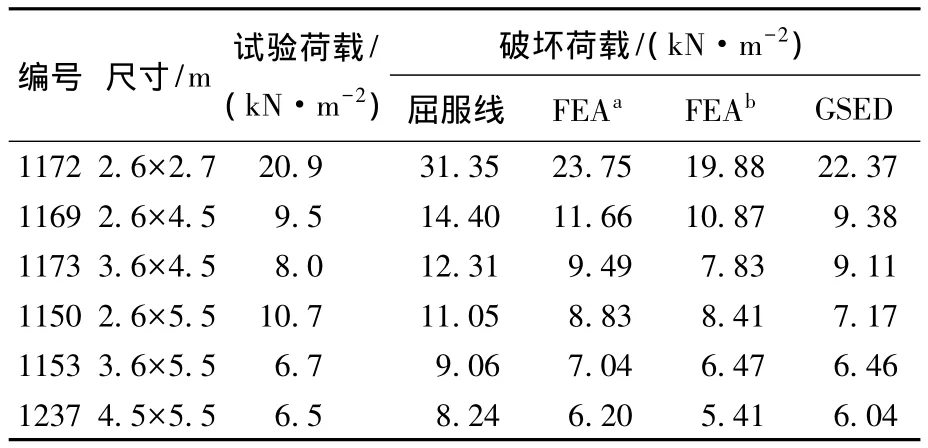
表1 基础板1244预测的破坏荷载
为了避免误差正负号相互抵消导致对精度的评价失效,本文以各方法预测破坏荷载与试验破坏荷载误差 (Eylt、EFEAa、EFEAb、EGSED)和相应的绝对平均误差作为评价预测精度的指标,例如,对屈服线方法,有
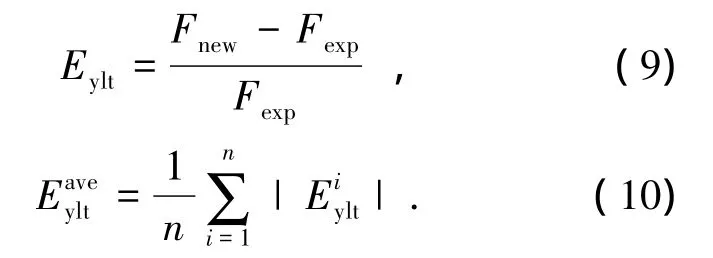
式中:Fnew为新板的预测破坏荷载,Fexp为新板的试验破坏荷载,n为墙板的数目.
对于厚度为0.215 m的试验板,以平面尺寸为4.5 m×4.5 m的试验板1244[3]作为基础板来预测相同约束、不同尺寸的新板的破坏荷载,其中1124表示试验板的编号,均布荷载通过气囊施加到墙板之上.新板的试验参数及3种方法得到的破坏荷载结果见表1.其中,有限元方法对于墙板的竖向约束分别按照简支和固支两种形式进行模拟.在表1中,第4列为应用屈服线方法计算出的破坏荷载;第5、6列为采用有限元方法计算出的破坏荷载,第5列中FEAa代表墙板的约束在有限元模型中按照三边固支模拟,第6列中FEAb代表墙板的约束在有限元模型中按照底边固支,两竖向边简支模拟得到的破坏荷载.第7列则是以墙板1244为基础板,根据广义应变能密度方法分别预测出的不同尺寸的新板的破坏荷载,在该方法中,约束均以三边简支来建立模型.
表2给出了3种方法预测结果的评价指标.可以看出,广义应变能密度方法预测出的破坏荷载较之屈服线方法平均精度提高约25%,与有限元方法相比,两者平均精度相差不大.
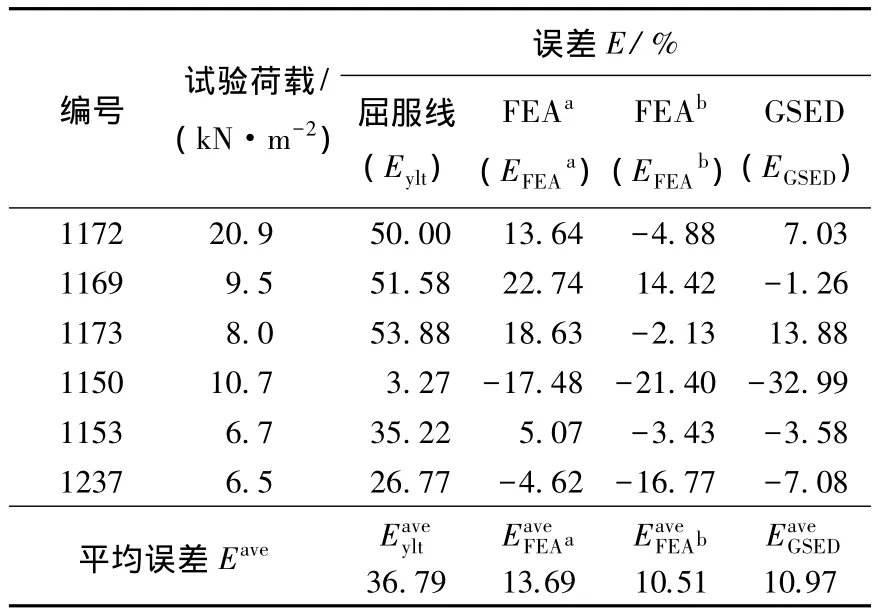
表2 基础板1244预测破坏荷载的误差
对于厚度为0.125 m的试验板,以平面尺寸3.6 m×4.5 m 的试验板 1109[3]为基础板来预测相同约束、不同尺寸的新板的破坏荷载,其中1109表示试验板的编号.新板的试验参数及应用3种方法预测出的破坏荷载见表3,3种方法预测结果的评价指标见表4.由表4的平均误差可看出,本文方法的预测精度较之屈服线方法高约5%,较FEAa高约4%,较FEAb高约16%.
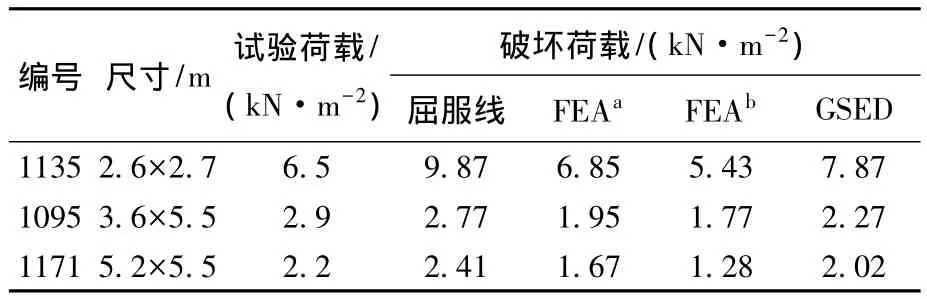
表3 基础板1109预测的破坏荷载
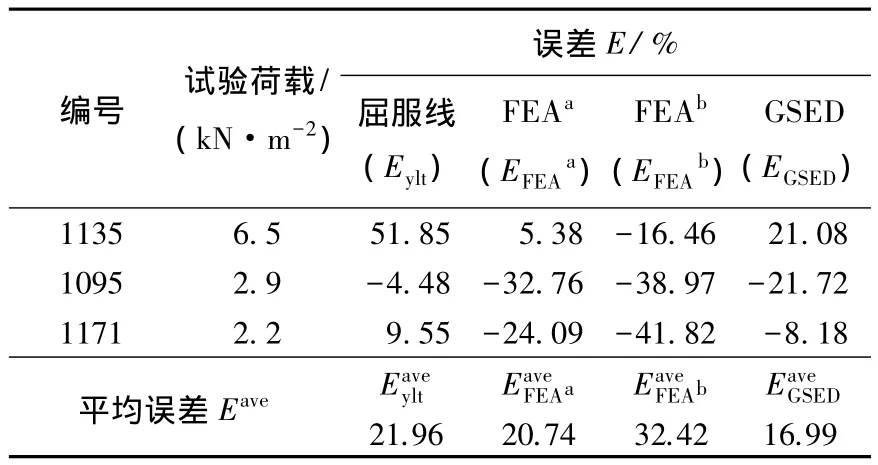
表4 基础板1109预测破坏荷载的误差
综合表2,4的误差结果可看出,对于两种不同厚度的砌体墙板,本文给出的算法在精度方面较之屈服线方法及有限元方法均有一定优势,或是精度高,或是简单通用.
对于四边约束的墙板,本文以Lawrence的四边简支试验板[7]为算例来验证本文方法的有效性.以 3 m×6 m×0.110 m 的试验板 Test8[7]为基础板来预测相同约束、不同尺寸新板的破坏荷载.新板的试验参数、基于广义应变能密度得到的破坏荷载及误差见表5.由表5预测结果可看出,对于四边约束的试验板,本文提出方法同样有效,且预测出的破坏荷载精度在工程许可范围内.
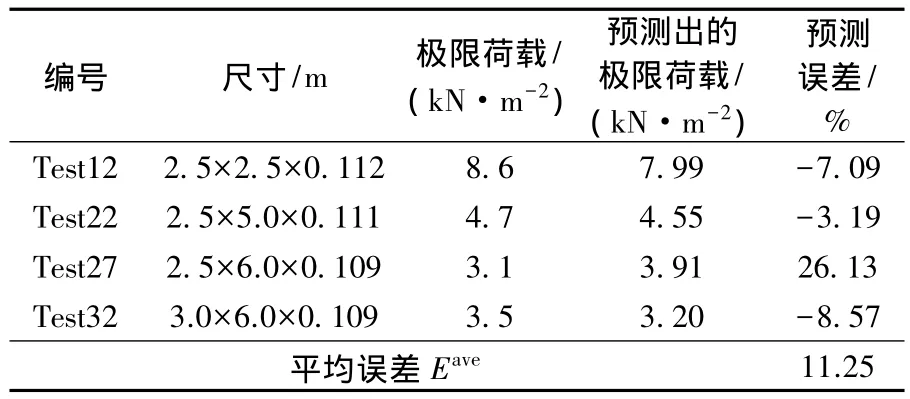
表5 基础板Test8预测的破坏荷载及误差
综合以上算例结果可知,本文提出算法对于两种常见约束形式,不同厚度的试验板都适用,具有一定的普适性和通用性.
传统的有限元方法,通常是以材性试验参数作为输入,因此其模拟的精度在很大程度上受到输入材料参数的影响,本文所提方法仅用到单位均布荷载作用下砌体墙板应变能密度的分布模式,不需要输入实际的材料性质参数,因此其预测的精度不受材性试验的影响,预测结果具有良好的稳定性.
另外,屈服线方法和有限元方法均以理想的假设为前提,本文所提方法是直接应用现有的试验记录、且没有经过任何处理作为输入,即该方法在进行破坏荷载预测时,材料或结构的初始缺陷,砌体本身的变异性也自然包含在其中.因此,本文提出方法为砌体墙板破坏荷载的预测提供了一种完全不同于现有分析方法的途径.
5 基础板选择的探讨
理论上说,本文方法对于基础板的选择没有限制,即任意已知的试验板均可作为基础板来预测其他相同约束形式,不同尺寸墙板的破坏荷载.
为了验证该方法对于基础板的选择无依赖性,本文以平面尺寸3.6 m×4.5 m的基础板1173[3]来预测表1中给出的厚度为0.215 m的试验墙板的破坏荷载,预测出的破坏荷载以及分别用屈服线方法及有限元方法计算得到的破坏荷载见表6,3种不同方法的计算或预测误差见表7.由表7相对误差绝对值的平均值可看出,本文方法预测精度较之屈服线方法高约17%,虽然较有限元方法低约5%,但仍在工程允许精度范围内.
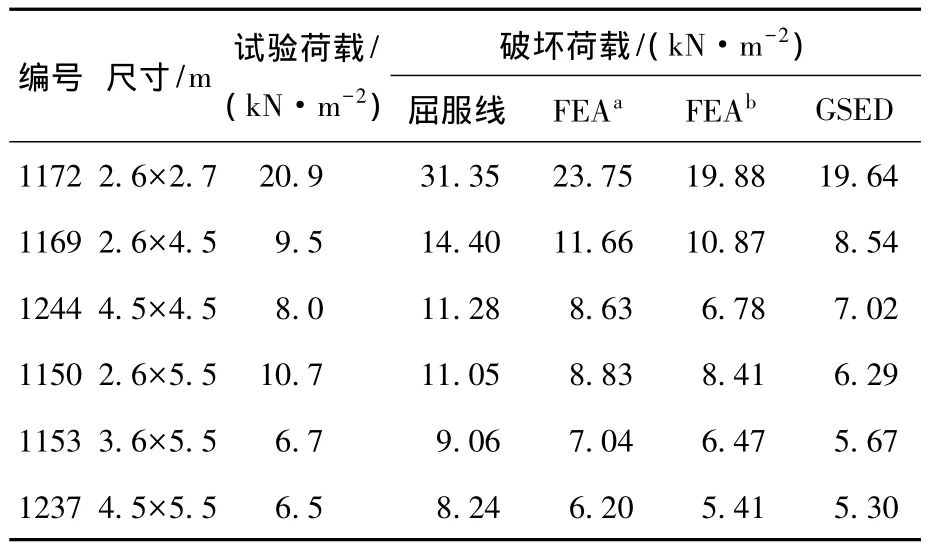
表6 基础板1173预测的破坏荷载
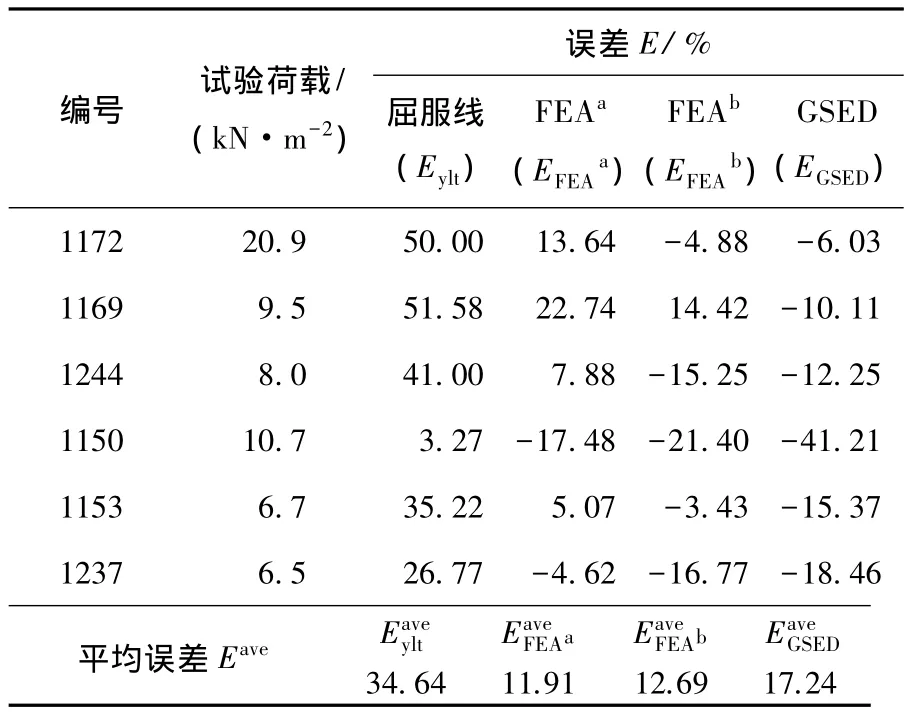
表7 基础板1173预测破坏荷载的误差
进而,本文给出了以两个不同的试验板(1244、1173)为基础板,用本文方法预测相同约束形式、不同尺寸的试验板的破坏荷载的误差,对比结果见表8.由表8可知,对于本文方法,试验板1244和1173均可作为基础板来预测其他的具有相同约束条件、不同尺寸的砌体墙板的破坏荷载,且预测出的破坏荷载精度均在工程许可范围内.因此,本文提出方法对于基础板的依赖性小,基础板的不同仅稍微影响到预测精度,这可能是由于不同的基础板所携带的变异信息不一样导致的.
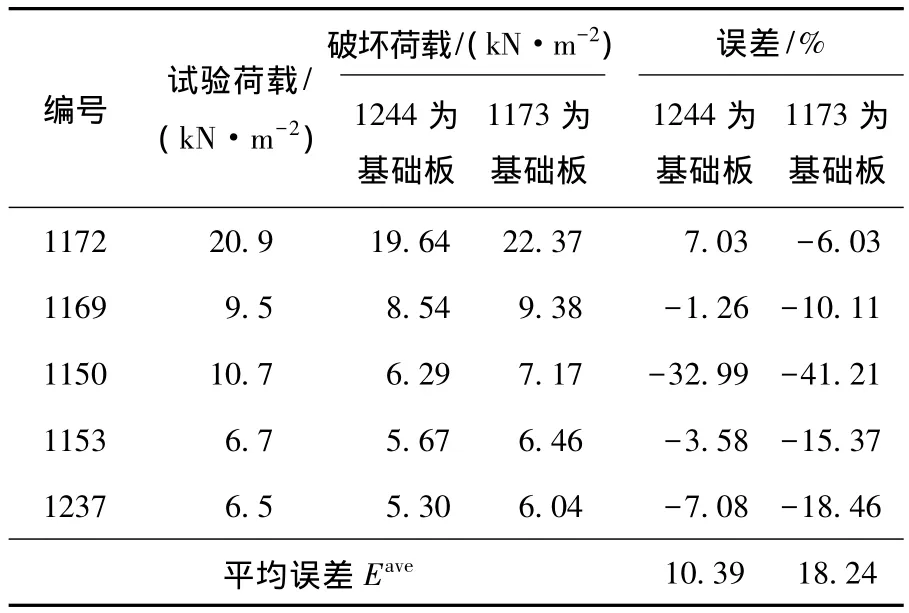
表8 基础板1244和1173预测出的破坏荷载及误差
6 结 论
1)揭示了面外均布荷载作用下墙板的广义应变能密度模式与墙板的破坏荷载存在相关性.
2)所建立的基于广义应变能密度预测墙板破坏荷载的方法,较之屈服线方法预测精度有较大提高;与有限元方法相比,预测精度基本相同,但建模相对简单、不受模型输入参数变异的影响.
3)基于广义应变能密度的方法是一个不同于传统分析方法的新方法,其独特之处在于能直接应用基础板试验结果预测新板破坏荷载,且不摈弃有限元法所反映的结构构造和工作行为的基本特征.
[1]Code of Practice for Use of Masonry.BS 5628 Part 1.Structural use of unreinforced masonry British Standards Institution(BSI)[S].London,1992.
[2]CHONG V L.The behavior of laterally loaded masonry panels with openings[D].Plymouth:University of Plymouth,1993.
[3]LEE S J,PANDE G N,MIDDLETON J,et al.Numerical modeling of brick masonry panels subjected to lateral loadings[J].Computer Structure,1996,61(4):735-745.
[4]LOURENCO P B.Anisotropic softening model for masonry plates and shells[J].Journal of Structural Engineering,2000,126(9):1008-1016.
[5]BRINKER R.Yield line theory and material properties of lateral loaded masonry panels[J].Masonry Int.,1984,1(4):19-26.
[6]FRIED A N.Laterally loaded masonry wall panels:the significance of analytical methods and material properties[D].London:South Bank Polytechnic,1989.
[7]LAWRENCE S J.Behaviour of brick masonry walls under lateral loading[D].Australia:University of South Wales,1983.
[8]ZHOU Guangchun,RAFIQ M Y,BUGMANN G,et al.Cellular automata model for predicting failure pattern of laterally loaded masonry wall panels[J].Journal of Computer in Civil Engineering,2006,20(6):400-409.
[9]ZHANG Yu,ZHOU Guangchun,XIONG Yi,et al.Techniques for predicting cracking pattern of masonry wallet using artificialneuralnetworksand cellular automata[J].Journal of Computer in Civil Engineering,2010,24(2):161-172.
[10]王勇,董毓利,邹超英.钢筋混凝土板的极限承载力计算[J].哈尔滨工业大学学报,2013,45(2):8-13.
[11]张明,张瑀,景志涛,等.预测单层柱面网壳破坏模式的细胞自动机方法[J].哈尔滨工业大学学报,2013,45(2):14-19.
[12]ZHOU Guangchun,PAN Deng,XU Xun,et al.Innovative ANN technique for predicting failure/cracking load of masonry panel under lateral load[J].Journal of Computing in Civil Engineering,2010,24(4):377-387.
Method for predicting failure load of masonry wall panel based on generalized strain energy density
HUANG Yanxia1,ZHANG Yu1,LIU Chuanqing2,ZHOU Guangchun1
(1.Key Lab of Structures Dynamic Behavior and Control,School of Civil Engineering,Harbin Institute of Technology,150090 Harbin,China;2.Shandong Provincial Academy of Building Research,250031 Jinan,China)
To predict the failure load of masonry wall panel,this paper extracts the strain energy density from the finite element analysis(FEA)of masonry wall panel under the evenly distributed unit load and develops a concept of generalized strain energy density(GSED).Then,by analyzing the GSED modes of both base and new panels,and the relationship between the failure loads of two panels is revealed.Hence,a GSED-based method is proposed.The case studies show that the GSED-based method is much more accurate than the yield line method.Comparing with the FEA method,the GSED-based method has nearly the same accuracy but a low sensitiveness to different material properties.Besides,The GSED-based method can directly apply the experimental data to predict the failure load of new panel,which provides a new way for predicting task.
masonry wall panel;generalized strain energy density;failure load;yield line method;FEA method
TU365
A
0367-6234(2014)02-0006-05
2013-04-02.
国家科技支撑项目(2013BAJ12B03).
黄艳霞(1984—),女,博士研究生;
周广春(1958—),男,教授,博士生导师.
周广春,gzhou@hit.edu.cn.
(编辑 赵丽莹)

